前回まで
改めて
機械学習を始めるにも、算数や数学がわからないと、入門書すら読めない。ただそこまで、ちゃんと解説してあるものもない。ということで最低限必要な数学基礎をこの記事で書けたらいいなと思っています。
環境
ほぼ影響ないですが、python3系を利用。
前提
四則演算や累乗(2乗とか3乗とか)がわかっていること。
三角関数
参照:https://jugo-blog.com/trigonometry
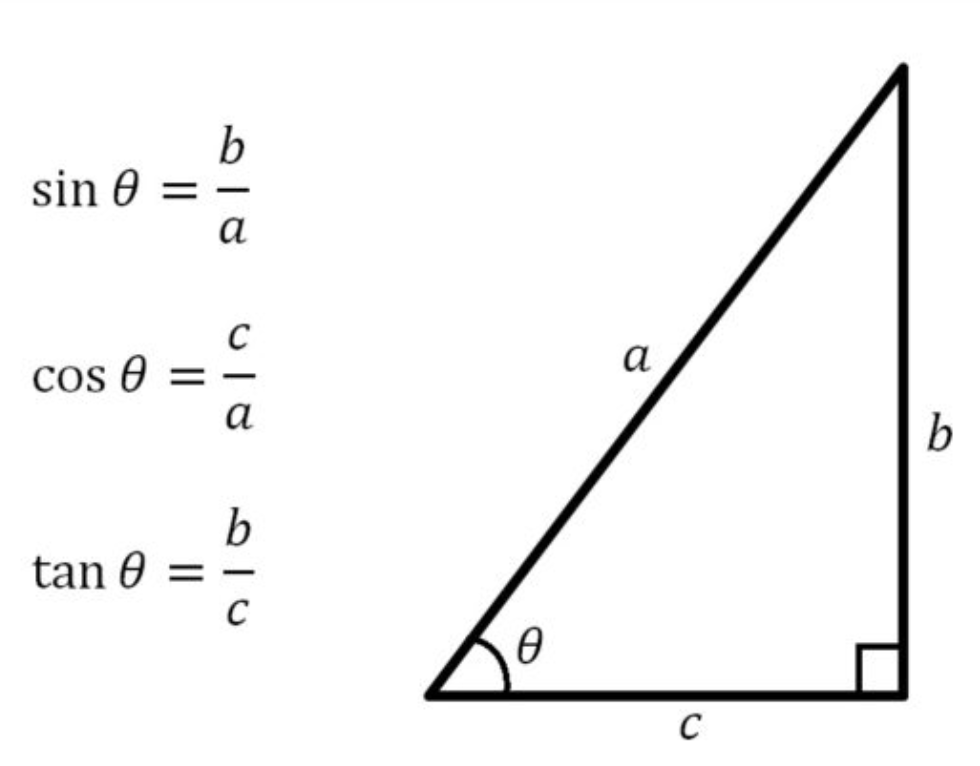
sin = 高さ/斜辺
cos = 底辺/斜辺
tan = 高さ/底辺
というもの。
半径が1の円の円周の上にある点の座標x,yとした時には
$cos\theta = \frac{x}{1}= x$
$sin\theta = \frac{y}{1}= y$
$tan\theta = \frac{y}{x} = \frac{sin\theta}{cos\theta} $
とすることができる。
また三平方の定理を使えば
$底辺^2 + 高さ^2 = 斜辺^2 $
において半径が1なら
$x^2 + y^2 = 1^2$
とすることができ
$cos^2\theta + sin^2\theta = 1$
とすることができる。
さらに
$cos^2\theta + sin^2\theta = 1$
の両辺をcos^2で割り
$\frac{cos^2\theta}{cos^2\theta}+ \frac{sin^2\theta}{cos^2\theta}= \frac{1}{cos^2\theta}$
となるので、これを整理すると
$1+ tan^2\theta= \frac{1}{cos^2\theta}$
という式を導き出すことができる。
※三平方の定理
$x^2+y^2=r^2$
$y^2 = r^2-x^2$
$y = \sqrt{r^2-x^2}$
$x = \sqrt{r^2-y^2}$
※汎用的に半径をrとおいたときに、、三角関数は以下のように変形していける
$cos\theta = \frac{x}{r}$
$sin\theta = \frac{y}{r}$
$cos\theta\times r = \frac{x}{r}\times r$
$sin\theta\times r = \frac{y}{r}\times r$
$cos\theta\times r = x$
$sin\theta\times r = y$
これらのように変形することで(x,y)という座標は($rcos\theta,rsin\theta$)と置き換えることができる。
sinとcosの変化
30度の時は、60度の時は、三角比が$1:2:\sqrt{3}$になります。
| 項目 | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| sin | 0 | $\frac{1}{2}=\frac{\sqrt{1}}{2}$ | $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1 = \frac{\sqrt{4}}{2}$ |
| cos | $1 = \frac{\sqrt{4}}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ | $\frac{1}{2}=\frac{\sqrt{1}}{2}$ | 0 |
sin/cosのグラフ
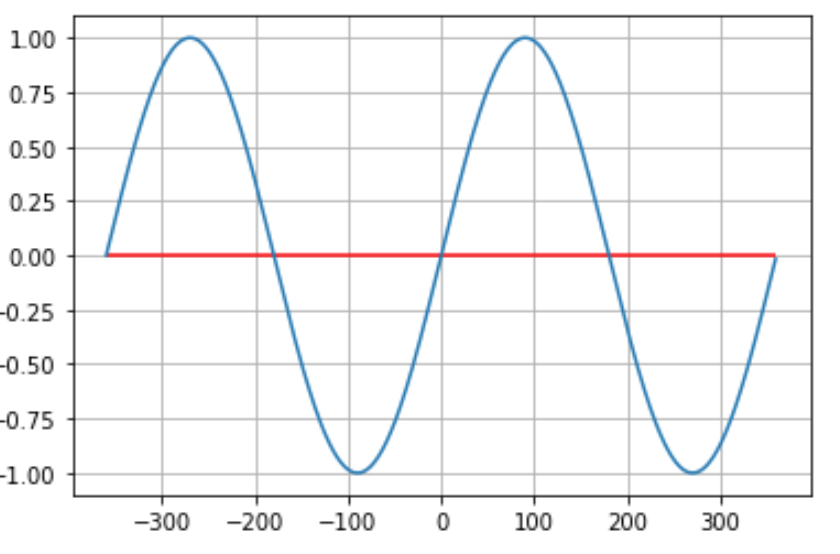
sinのグラフは、原点を対称点とする点対称な関数である奇関数と言います。
$
f(-x) = -f(x)
$
x = np.arange(-360,360,1)
y = np.sin(np.radians(x))
plt.plot(x,y)
plt.grid()
plt.hlines(0,-360, 360,color = "red")
cosのグラフは、y軸に関して対称な関数である奇関数と言います。
$
f(-x) = f(x)
$
x = np.arange(-360,360,1)
y = np.cos(np.radians(x))
plt.plot(x,y)
plt.grid()
plt.vlines(0,-1, 1,color = "red")

π
πは円周率のことをさしており、円周率とは「円周と直径の比」つまり、直径の3.14倍が円周の長さですよという話になってくる。
よく見る
2\pi r
がこれのことというのがわかりました。
度数法と弧度法
180°というのは度数法、弧度法radianは弧の長さの比率(扇の弧の長さは角度に比例する)で表した角度の単位です。計算式としてはradianは、「円(扇形)の孤の長さ(L)÷円の半径(r)」によって求められる値のことで、radianの単位は、[rad(ラジアン)]です。
1rad = 円の半径rと弧の長さが等しくなる時の中心角の大きさ\\
\begin{align*} 1 \, \mathrm{rad} &= 360^\circ \times \frac{r}{2 \pi r} \\ &= \frac{180^\circ }{\pi} \\ &\approx {57.2958}^\circ \end{align*}
また三角関数などを扱う場合に、半径rを1として扱うことが多く、その場合は、孤の長さがradianとなります。
半円形であれば
$2\pi{r}\div 2 = \pi{r}$で孤の長さは定義され
半径1であれば
$\pi = 3.14$
となります。
math.radians(180)
3.141592653589793
np.degrees(3.141592653589793)
180.0
円形であれば
$2\pi{r}$で孤の長さは定義され
半径1であれば
$2\pi = 6.28$
となります。
import math
math.radians(360)
6.283185307179586
np.degrees(6.283185307179586)
360.0
この度数法を弧度法に変換して、三角関数を求めます。
※感覚的にmath.sin(30)と変換しないでやるのは間違いです。
import math
print(math.sin(math.radians(30)))
print(math.sin(math.radians(60)))
print(math.sin(math.radians(90)))
print(math.sin(math.radians(120)))
print(math.sin(math.radians(150)))
print(math.sin(math.radians(180)))
# 0.49999999999999994
# 0.8660254037844386
# 1.0
# 0.8660254037844388
# 0.49999999999999994
# 1.2246467991473532e-16
これを使えば円をかけます。
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
th = np.arange(0,359)
x = np.cos(np.radians(th))
y = np.sin(np.radians(th))
plt.plot(x,y)
plt.axis("equal")
plt.grid()
plt.show()

三角比と角度

$\tan\theta = \frac{b}{c} = \frac{高さ}{底辺}$
これを変形すれば、直角を挟む2つの直線(底辺と高さ)から角度を求めることができます。
$\theta = tan^{-1}\big(\frac{b}{c}\big)$
これは−1乗ではなく、tanの逆関数を意味しており、アークタンジェントと言います。
pythonではnp.arctan2(高さ、底辺)を使うとradianが帰ってくるので、これをdegrees()で度数に変換します。
以下では$\sqrt{3}$と1で角度を求めます。
# 角度を求める
import numpy as np
round( np.degrees(np.arctan2(np.sqrt(3),1))) #-> 60.0
絶対値とユークリッド距離
k-meansとかで使いますね。
絶対値
$|-5|=5$ ,$|5|=5$
ユークリッド距離(2点を結んだ距離)1次元
$||A-B||$
ユークリッド距離(2点を結んだ距離)2次元→三平方の定理
$||A-B||=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$
ユークリッド距離(2点を結んだ距離)3次元→三平方の定理
$||A-B||=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2}$
ここまで
ベクトルのところとも繋がりが強いので、とても大事です。
※不明点や不備があればコメントください。
次回は数列について投稿していきます。