[python]算数・数学⑦~ベクトル~

前回まで

前回はこちら

改めて

機械学習を始めるにも、算数や数学がわからないと、入門書すら読めない。ただそこまで、ちゃんと解説してあるものもない。ということで最低限必要な数学基礎をこの記事で書けたらいいなと思っています。

環境

ほぼ影響ないですが、python3系を利用。

前提

四則演算や累乗（2乗とか3乗とか）がわかっていること

ベクトル

以下のこういうやつです。方向と大きさを表すことができます。

\vec{a}\\
\vec{AB}

※$a$(小文字の太字)と表現する場合や、二重に書かれた$\mathbb{a}$もあります。

座標上でのベクトルを表す

例えばAの座標が（3,4）だった場合に、ベクトルは以下のように表せます。

\vec{OA} = (3,4)

\vec{OA} = \left( \begin{array}{cc} 3\\ 4\\ \end{array} \right)

ベクトルの角度

座標がわかっている時は、アークタンジェントを使って角度を求めることもできます。

\theta = tan^{-1}\big(\frac{y}{x}\big)

np.arctan2(底辺、高さ)を使うとラジアンが帰ってくるので、これをdegrees()で度数に変換することで角度が求められる。

np.degrees(np.arctan2(4,3))
53.13010235415598

ベクトルの大きさ

底辺(座標でいうx)の２乗と高さ(座標でいうy)の2乗の和は斜辺の2乗になります(三平方の定理)。大きさのみをもつものを、「スカラー」といいます。

(x1-x2)^2+(y1-y2)^2=AB^2\\
\sqrt{(x1-x2)^2+(y1-y2)^2}=|\vec{AB}|\\

三次元ベクトルは以下

\sqrt{x^2+y^2+z^2}=|\vec{v}|\\

ちなみに大きさが１のベクトルのことを単位ベクトル$\vec{e}$と言います。

\vec{e} = \frac{\vec{AB}}{\vec{|AB|}}

ベクトルの演算

ベクトルの足し算

\vec{a}+\vec{b}=\left( \begin{array}{cc} a_1\\ a_2\\ \end{array} \right)+\left( \begin{array}{cc} b_1\\ b_2\\ \end{array} \right)=\left( \begin{array}{cc} a_1+b_1\\ a_2+b_2\\ \end{array} \right)

足し算するベクトルの成分の数（次元）は同じでなければいけません。

import numpy as np
a = np.array([3,1])#ベクトルAの成分
b = np.array([2,-2])#ベクトルBの成分
a+b

ベクトルの引き算

\vec{a}-\vec{b}=\left( \begin{array}{cc} a_1\\ a_2\\ \end{array} \right)-\left( \begin{array}{cc} b_1\\ b_2\\ \end{array} \right)=\left( \begin{array}{cc} a_1-b_1\\ a_2-b_2\\ \end{array} \right)

引き算するベクトルの成分の数（次元）は同じでなければいけません。

考え方として$\vec{a}-\vec{b} = \vec{a}+(-\vec{b})$なので$\vec{b}$を逆向きにしたものを足すのと同じ考え方でグラフでもかくことができます。もちろん始点を揃えて、bの終点からaの終点に向けたベクトルとして問題ありません。

import numpy as np
a = np.array([3,1])#ベクトルAの成分
b = np.array([2,-2])#ベクトルBの成分
a-b

スカラー倍

\vec{a}=k\vec{a}=\left( \begin{array}{cc} ka_1\\ ka_2\\ \end{array} \right)

import numpy as np
a = np.array([3,1])#ベクトルAの成分
k=3
a*k

内積

内積はドット積とも呼ばれる。以下のようなもの。これはベクトルではなくスカラー（実数）で返ってきます。

<\vec{a},\vec{b}> = \vec{a}・\vec{b} =a_1b_1+a_2b_2+\dots+a_nb_n = \sum_{i=1}^na_ib_i\\

<\vec{a},\vec{b}> = \vec{a}・\vec{b} = |\vec{a}||\vec{b}|cos\theta　= a_1b_1+a_2b_2\dots

そして言語処理でも利用するcos類似度に利用できるように変形することもできます。

|\vec{a}||\vec{b}|cos\theta= a_1b_1+a_2b_2\\

cos\theta= \frac{a_1b_1+a_2b_2}{|\vec{a}||\vec{b}|}

計算の要素はこんな感じで用意する

\vec{a} = \left( \begin{array}{cc} x_2-x_1\\ y_2-y_1\\ \end{array} \right)\\
\vec{b} = \left( \begin{array}{cc} x_4-x_3\\ y_4-y_3\\ \end{array} \right)\\

\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=|\vec{a}|\\
\sqrt{(x_4-x_3)^2+(y_4-y_3)^2}=|\vec{b}|

pythonで行うと

import math
import numpy as np

#座標を作る
a = np.array([3,6])
b = np.array([4,2])
c = np.array([1,5])
d = np.array([5,8])

#ベクトルを作る
veca = b-a
vecb = d-c

#スカラを求める#三平方の定理
norm_a = np.linalg.norm(veca)
norm_b = np.linalg.norm(vecb)

#内積（ドット積）を求める
dot_ab = np.dot(veca,vecb)

#角度を計算#アークコサインを使う#孤度を度数に変換する
cos_theta = dot_ab/(norm_a*norm_b)
radians = math.acos(cos_theta)
degrees = math.degrees(radians)
print(degrees)
# -> 112.83365417791754

ポイント：cosは0~90度の時に正をとり、90~180の時に負の数を取る(0の時は直交)
ポイント：絶対値を含む計算式のため、内積自体の正と負はcosによって決まるため、ベクトルの位置がどれくらい離れているかわかる
→内積がマイナスの時はすごく離れていて、プラスの時は近い

ということでcos類似度は、ベクトルが近い関係にあるかどうかを見るものということです。そしてこれは２次元だけでなく複数次元でも表現をすることができます。これで文章などの類似度をみることもできます。

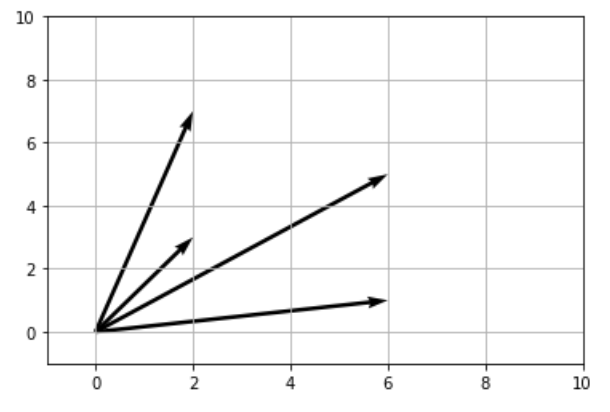
わかりやすく可視化までざっと

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

#座標を作る
o = np.array([0,0])
a = np.array([2,7])
b = np.array([6,1])
c = np.array([2,3])
d = np.array([6,5])

#ベクトル
oa = a-o
ob = b-o
oc = c-o
od = d-o

#スカラ
norm_a = np.linalg.norm(oa)
norm_b = np.linalg.norm(ob)
norm_c = np.linalg.norm(oc)
norm_d = np.linalg.norm(od)

#内積
dot_ab = np.dot(oa,ob)
dot_ac = np.dot(oa,oc)
dot_ad = np.dot(oa,od)
dot_bc = np.dot(ob,oc)
dot_bd = np.dot(ob,od)
dot_cd = np.dot(oc,od)

#cos
cos_thab = dot_ab/(norm_a*norm_b)
cos_thac = dot_ac/(norm_a*norm_c)
cos_thad = dot_ad/(norm_a*norm_d)
cos_thbc = dot_bc/(norm_b*norm_c)
cos_thbd= dot_bd/(norm_b*norm_d)
cos_thcd = dot_cd/(norm_c*norm_d)

#ベクトルの関係とcosの辞書を作成
cos_list = {"ab":cos_thab,"ac":cos_thac,\
            "ad":cos_thad,"ad":cos_thad,\
            "bc":cos_thbc,"bd":cos_thbd,\
            "cd":cos_thcd}

#cosの類似度順(1に近い順)に並び替え 
sorted(cos_list.items(), key=lambda x:x[1],reverse=True)
# ->
[('cd', 0.9587981127083873),
 ('ac', 0.9524241471993242),
 ('bd', 0.8630144693469346),
 ('ad', 0.8265992475892193),
 ('bc', 0.6839411288813299),
 ('ab', 0.4290568145682877)]

plt.figure()

# 矢印（ベクトル）の始点
X = o[0],o[0],o[0],o[0]
Y = o[1],o[1],o[1],o[1]

# 矢印（ベクトル）の成分
U = a[0],b[0],c[0],d[0]
V = a[1],b[1],c[1],d[1]

# 矢印（ベクトル）
plt.quiver(X,Y,U,V,angles='xy',scale_units='xy',scale=1)

# グラフ表示
plt.xlim([-1,10])
plt.ylim([-1,10])
plt.grid()
plt.draw()
plt.show()

外積

外積と内積は全く違います。まず外積は三次元空間にしか存在しないです。そして内積の結果はスカラだが、外積はベクトルになります。

いくつかの特徴があり
・aとbの外積は、aからbに向かう方向の右ねじの法則のベクトルになる（法線ベクトル）
・つまり右手で棒を掴んだ時の、人差し指がaからbの向きだとした時の親指が外積の向きになります
・そして外積のベクトルの大きさはaとbのベクトルが作る平行四辺形と等しい(詳細は割愛します)

pythonでやってみます。

#外積を計算してみる
import numpy as np
a = np.array([0,1,1])
b = np.array([2,3,4])
np.cross(a,b)
# ->array([ 1,  2, -2])

ノルム

この項目は正則化の時にとても大事な項目になります。

この投稿ではいくらか「ベクトルの大きさ」を

\sqrt{(x1-x2)^2+(y1-y2)^2}=|\vec{AB}|

と扱っていました。この求め方は$L2$ノルムと呼び、ユークリッド距離と言います。（要は直線距離です）

aのL2ノルム = ||a||_2 = \sqrt{\sum_{i=1}^na^2_i}=\sqrt{(a^2_1+a^2_2+・・・+a^2_n)}

一方で「東京駅まで右に100m、左に500m、右に300mの計900m」のように足し合わせる求め方を$L1$ノルムと言います。この距離をマンハッタン距離と言います。

aのL1ノルム = ||a||_1 = |a|_1+|a|_2+・・・+|a|_n = \sum_{i=1}^n|a_i|

線形回帰モデルの係数（重み）をこれらの方法で積み上げたものを正則化項として設けることで、係数（重み）が大きくならないようにする(過学習を防ぐ)ことを正則化と言います。

ここまで

次回は行列について投稿していきます。