テトレーションカオスと戯れる 2 - 高速化編

本記事では「テトレーションカオスと戯れる」 にて取り上げた、テトレーションフラクタルを視覚化するプログラムの高速化を試みます。

想定する読者

• テトレーションフラクタルの描写速度を上げたい方 (10倍以上高速化できます)
• python のマルチプロセッシングライブラリの Pool.map のサンプルプログラムを探している方
• cython による python の高速化サンプルプログラムを探している方

この記事のプログラムを動かすには、python 3.6 以上の実行環境に、matplotlib, numpy, cython をインストールしておく必要があります。インストール方法は皆様の環境によって変わるので割愛させていただきますが、一般的には
pip install matplotlib numpy cython
でできると思います。

高速化の戦略

今回高速化を試みるプログラムは、「テトレーションカオスと戯れる」 に含まれる、tetration.py というプログラムです。これは下図のように3つの関数から構成されています。

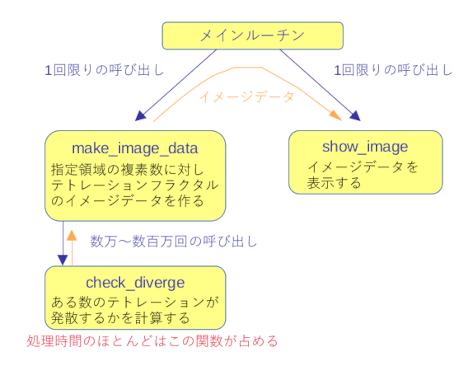
実行時間は check_diverge 関数がほとんどを占めます。なのでプログラムの高速化を図るには check_diverge 関数の実行時間を短縮することに集中すれば良いでしょう。
check_diverge 関数は次のような特徴があります。この特徴を元に戦略を立てましょう。

• 呼び出される回数が多い。デフォルトは16800回だが、作成するイメージの解像度を上げるためにプログラムに手を加えると、呼び出し回数は数十万〜数百万回に及ぶ。
• 関数の戻り値は引数だけに依存する。呼び出される順序と戻り値には関係が無い。
• 複素数のべき演算をひたすら繰り返す関数である。

関数が何度も呼び出されるなら、高速化の常套手段はマルチスレッディング、もしくはマルチプロセッシングによる同時実行です。きょう日のCPUなら同時に4つ以上、Threadripper 3990X なんかだったら128ものタスクを同時に並列実行できます。
マルチスレッディングとマルチプロセッシングならどちらが高速化できるでしょうか？一般的にはマルチスレッディングのほうが軽くて早いのですが、python は GIL の制約でマルチスレッド化しても全部の仮想CPUをフルにブン回すことが原則できないので今回はマルチプロセッシングの手段を取ることにします。
（pythonのマルチスレッディングライブラリの、concurrent.futures.ThreadPoolExecutor も試してみたのですが、このプログラムのようにひたすらCPUをブン回すケースではむしろ遅くなってしまいました。）

マルチプロセッシング プログラムでは、関数を実行するプロセスを生成しないといけませんが、プロセスを作るのはとても重い仕事です。どのくらい重いかというと、プロセスを1個作るには check_diverge 関数を1回実行するよりもずっと時間がかかってしまいます。なので、生成するプロセスの数は同時に実行できる最大の数、すなわち CPU の仮想コア数だけにとどめて、生成したプロセスをプールして、各プロセスにcheck_diverge 関数を順繰りに実行させることにします。 python ではプロセスプールを扱うクラスとして、multiprocessing.Pool が用意されているのでこれを使いましょう。
multiprocessing.Pool で関数を実行するメソッドはいくつかあるのですが、 計算をする順番と結果に関係のない大量のタスクを一気に処理するなら map が処理が早く、また使い方も簡単なのでこれを使います。

python プログラムの高速化手段として、cython もあります。cython は python のコードを c++ のコードに変換・コンパイルする処理系で、プログラムの一部を静的な実行形式にコンパイルすることにより高速化が図れます。cython も使ってみましょう。

戦略のまとめ

• マルチプロセッシングクラスの multiprocessing.pool を使い、全部の CPU コアをブン回して一気に処理するぞ！
• cython を使い、プログラムの一部をコンパイルして高速化するぞ！

高速化を試みるプログラム

高速化を試みるプログラムはこれ↓です。

tetration.py

import matplotlib.pyplot as plt
import numpy as np
import time

####  最初に各種パラメーターを設定します ###
## どの領域の複素数 z を計算するのか ##
RealMin = -2.0    # 実数部の最小値
RealMax = 2.0     # 実数部の最大値
ImgMin = -2.0     # 虚数部の最小値
ImgMax = 2.0      # 虚数部の最大値
Divide = 401      # 計算する領域で、実数軸・虚数軸をいくつに区切るか. 始点と終点を含む
## グラフのパラメーター ##
LazyInf = 200   # z のべき演算を LazyInf 回繰り返して発散しなければ、∞回でも収束するとみなす
GWidth = 10     # matplotlib で描く図の幅
GHeight = 10    # matplotlib で描く図の高さ
Colormap = "gist_heat_r" # 図の色使い。 "magma"  "cool"  "Reds" "viridis" などお好みで選んで

def check_diverge(z):
    """ z↑↑n の計算で n が有限の値で発散するかをチェックする。最大 z↑↑LazyInf まで調べる。
    """
    tet = 1.0    # テトレーション演算の途中結果を格納する変数
    for n in range(LazyInf+1):
        try:
            tet = z ** tet
            if abs(tet-z) > 1000000000:  # 途中が大きな数になったら、発散するとみなす
                break
        except:
            break   # エラーが発生したら、発散するとみなす
    return(n)  # 途中で発散したら何回目で発散したかが返る。発散しなかったら LazyInf が返る。

def make_image_data(r_min, r_max, i_min, i_max, divide):
    """ 指定された領域を実数部、虚数部ともに divide 個に分割した numpy の配列を作り、
        z↑↑n が n がいくつで発散するかを格納する。
    """
    x = np.linspace(r_min, r_max, divide)            # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, divide)            # 計算する z の虚数部を格納する配列
    img = np.zeros((y.size, x.size), dtype=np.int32) # n がいくつで発散するかを格納する配列
    for i_index in range(y.size):
        for r_index in range(x.size):
            img[i_index, r_index] = check_diverge(complex(x[r_index], y[i_index]))
    return(img)

def show_image(r_min, r_max, i_min, i_max, img):
    """ matplotlib の pcolormesh を使って結果を図にする。"""
    fig, ax = plt.subplots(figsize=(GWidth, GHeight))
    x = np.linspace(r_min, r_max, img.shape[1])    # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, img.shape[0])    # 計算する z の虚数部を格納する配列
    X,Y = np.meshgrid(x, y)
    ax.pcolormesh(X, Y, img, cmap=Colormap)
    ax.set_xlabel("Real", fontsize=GWidth*1.5)
    ax.set_ylabel("Imaginary", fontsize=GWidth*1.5)
    plt.show()

if __name__ == "__main__":
    start = time.time()
    diverge_img = make_image_data(RealMin, RealMax, ImgMin, ImgMax, Divide)
    print(f"total time {time.time()-start} sec\n")
    diverge_img = np.log(diverge_img)  # 図の色使いを派手にするためデータのダイナミックレンジを小さく
    show_image(RealMin, RealMax, ImgMin, ImgMax, diverge_img)

実行すると、テトレーションフラクタルのイメージが表示され、イメージ作成に要した時間が表示されます。
私のPC(Intel Core i7-6820HQ)では イメージ作成に平均 8.7 秒かかりました。

Pool.map によるマルチプロセッシング

上は map メソッドを実行している multiprocessing.Pool クラスのポンチ絵です。
Pool クラスのオブジェクトは関数を実行するワーカープロセスを複数持っています。Pool クラスのオブジェクトにマルチプロセスで実行させる関数と、その関数の引数のコレクションを与えて map メソッドを適用すると、Pool クラスはコレクションから引数を一つを選択して空いてるワーカープロセスに関数を処理をさせます。Pool クラスはワーカー達が休む暇の無いよう効率的に仕事をスケジューリングするので、CPUを 100% に近い利用率で回してくれます。

では元のコードに手を入れていきましょう。
手を加えるのは check_diverge 関数を呼び出す make_image_data 関数だけです。5点手を入れます。
　① multiprocessing ライブラリをインポートする
　② Pool クラスのオブジェクトを作る
　③ map メソッドに与える引数のコレクション(リスト)を用意する
　④ map メソッドを実行する
　⑤ 戻り値は1次元のリストなので、これを2次元の numpy オブジェクトに変換する

オリジナル

def make_image_data(r_min, r_max, i_min, i_max, divide):
    x = np.linspace(r_min, r_max, divide)            # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, divide)            # 計算する z の虚数部を格納する配列
    img = np.zeros((y.size, x.size), dtype=np.int32) # n がいくつで発散するかを格納するndarray
    for i_index in range(y.size):
        for r_index in range(x.size):
            img[i_index, r_index] = check_diverge(complex(x[r_index], y[i_index]))
    return(img)

Pool.map を使った改変版

import multiprocessing as mp  # ①

def make_image_data(r_min, r_max, i_min, i_max, divide):
    check_diverge_processes = mp.Pool(mp.cpu_count())  # ②
    x = np.linspace(r_min, r_max, divide)       # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, divide)       # 計算する z の虚数部を格納する配列
    zs = [complex(x[r_index], y[i_index]) \
        for i_index in range(divide) for r_index in range(divide)]  # ③
    ns = check_diverge_processes.map(check_diverge, zs)  # ④
    img = np.array(ns, dtype=np.int32).reshape(divide, divide)   # ⑤
    return(img)

解説していきます。
#①: multiprocessing をインポートしてます。
#②: Poolオブジェクトは、Pool(作成するワーカーの数) で生成されます。ここではワーカーの数としてマシンが持ってる仮想CPUの数 (mp.cpu_count()) を明示的に指定してますが、実は引数を省略した場合のデフォルト値も仮想CPUの数です。
#③: オリジナルのコードでは、check_diverge 関数に与える引数を for 文で生成して、引数を生成したつど関数を実行していますが、Pool.map ではあらかじめ全部の引数を一次元のコレクションで用意する必要があります。③ではfor 文で作っていた引数を内包表記で一次元のリストにしています。
なお、Pool には、ワーカーたちに与える引数をコレクションではなくイテレータとして与える、imap メソッド、 imap_unordered メソッドもあります。
#④: ②で作ったPool オブジェクトの map メソッドを呼んでます。この一行だけで Pool はプロセスのスケジュールをして check_diverge 関数をみっちり実行してくれます。簡単ですね。
#⑤: map メソッドの戻り値は1次元のリストです。これを オリジナルの make_image_data 関数の戻り値と同じ型に変換してます。

Pool.map の高速化結果

tetration.py の関数 make_image_data を オリジナル版から Pool.map を使った改良版に差し替えたところ、私のPCではイメージデータの作成に要する時間がオリジナルの8.7秒から2.3秒に短縮できました。約3.8倍の高速化です。

cython による高速化

cython は python のコードの一部を静的な実行形式にコンパイルすることで高速化を図ります。
手順としては、3つのステップを踏みます。

1. 静的な実行形式にコンパイルできるように、一部の python の関数を書き換える
2. コンパイルする
3. コンパイルした関数を python のプログラムにインポートして実行する

cython による高速化 パート1 - 関数の書き換え

今回は、make_image_data と check_diverge の2つの関数を cython 化します。
cython化で高速化を図るには、2つのアプローチがあります。一つは使用する変数の型を宣言することで、もう一つはプログラムのアルゴリズムを見直すことです。前者は簡単な機械的な作業ですが、後者はコンパイル後のマシン語コードの最適化を考えつつコードを修正しないとならないので難しい作業になります。今回はアルゴリズムの手直しまでは手が回らず、変数の型指定だけにしてます。もしアルゴリズムの改良で高速化が図られましたらご教示いただけるとありがたいです。
cython 化したコードは下記です。cython コードのファイルには .pyx という拡張子をつけます。このコードを tetration_funcs.pyx というファイル名で保存してください。

tetration_funcs.pyx

import cython          # ①
import numpy as np
cimport numpy as np    # ②    
import multiprocessing as mp
LazyInf = 200   # z のべき演算を LazyInf 回繰り返して発散しなければ、∞回でも収束するとみなす

def check_diverge(double complex z):  # ③
    cdef:              # ④
        int lazy_inf, n
        double complex tet
    lazy_inf = LazyInf
    tet = 1.0
    z = z + 1e-100j   # ⑤ バグ回避。詳細は記事を参照してください
    for n in range(1, lazy_inf+1):
        try:
            tet = z ** tet
            if abs(tet) > 100000000.0:
                break
        except:
            break  # エラーが発生したら、発散したとみなす
    return(n)  # 発散しなかったら LazyInf が返る。途中で発散したら何回目の計算で発散したかが返る


def make_image_data(int r_min, int r_max, int i_min, int i_max, int divide):    # ③
    cdef:   # ④
        np.ndarray[double, ndim=1] x, y
        int r_index, i_index
        np.ndarray[int, ndim=2] img
    x = np.linspace(r_min, r_max, divide)
    y = np.linspace(i_min, i_max, divide)
    zs = [complex(x[r_index], y[i_index]) for i_index in range(divide) for r_index in range(divide)]
    check_diverge_processes = mp.Pool(mp.cpu_count())
    ns = check_diverge_processes.map(check_diverge, zs)
    img = np.array(ns, dtype=np.int32).reshape(divide, divide)   # 二次元のndarrayに変換
    return(img)

オリジナルとの変更点を解説します。
#① cython のコードには import cython という文が必要です。
#② numpy を使う場合、"cimport numpy as np " を書いておかないと、numpy　のオブジェクトを静的な変数として型宣言することができません。
#③ 関数の引数も型宣言をします。そうしないとコンパイルしても高速化が望めません。
#④ 関数の最初に、 cdef: ステートメントを書き、ここで関数で使用する変数の型を宣言します。書き方は、"型の名前 変数1 [, 変数2 [, 変数3, [...]]]" です。具体的な書き方はコードを参照してください。
#⑤ c++ の演算ライブラリにバグ(仕様?)があって、負の実数のべき演算に複素数の結果を返さず nan を吐きます。例えば、z = -1.4 としたとき z ** z の計算値は複素数 (-0.1929 + 0.5938j) なのですが、c++ は nan を返してきます。一方で複素数のべき演算にはきちんと値を返します。よって z に負の実数が与えられた時のバグ対策のため、計算結果に影響が出ないと思われる極小の複素数を足して z を複素数化しています。

cython による高速化 パート2 - コンパイル

パート1 で作成した、tetration_funcs.pyx をコンパイルするには python のプログラムが必要です。次のコードを setup_tetration_funcs.py というファイル名で、tetration_funcs.pyx と同じディレクトリに保存してください。

setup_tetration_funcs.py

from distutils.core import setup, Extension
from Cython.Build import cythonize
from numpy import get_include # cimport numpy を使うため

ext = Extension("tetration_funcs", sources=["tetration_funcs.pyx"], include_dirs=['.', get_include()])
setup(name="tetration_funcs", ext_modules=cythonize([ext]))

python setup_tetration_funcs.py
としてプログラムを実行すると、"tetration_funcs.cpython-39-x86_64-linux-gnu.so" のような名前のファイルができたと思います(環境によってファイル名は異なる)。 このファイルを python から見えるフォルダに置けば import tetration_funcs と書くことで、cython 化した make_image_data と check_diverge を使うことが可能になります。

cython による高速化 パート3 - cython 化した関数の使用

コードは次のようになります。オリジナルのプログラムとの違いは"from tetration_funcs import make_image_data" という行があるだけです。

import matplotlib.pyplot as plt
import numpy as np
import time
from tetration_funcs import make_image_data

####  最初に各種パラメーターを設定します ###
## どの領域の複素数 z を計算するのか ##
RealMin = -2.0    # 実数部の最小値
RealMax = 2.0     # 実数部の最大値
ImgMin = -2.0     # 虚数部の最小値
ImgMax = 2.0      # 虚数部の最大値
Divide = 401      # 計算する領域で、実数軸・虚数軸をいくつに区切るか. 始点と終点を含む
## グラフのパラメーター ##
LazyInf = 200   # z のべき演算を LazyInf 回繰り返して発散しなければ、∞回でも収束するとみなす
GWidth = 10     # matplotlib で描く図の幅
GHeight = 10    # matplotlib で描く図の高さ
Colormap = "gist_heat_r" # 図の色使い。 "magma"  "cool"  "Reds" "viridis" などお好みで選んで

def show_image(r_min, r_max, i_min, i_max, img):
    fig, ax = plt.subplots(figsize=(GWidth, GHeight))
    x = np.linspace(r_min, r_max, img.shape[1])      # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, img.shape[0])      # 計算する z の虚数部を格納する配列
    X,Y = np.meshgrid(x, y)
    ax.pcolormesh(X, Y, img, cmap=Colormap)
    ax.set_xlabel("Real", fontsize=GWidth*1.5)
    ax.set_ylabel("Imaginary", fontsize=GWidth*1.5)
    plt.show()

if __name__ == "__main__":
    start = time.time()
    diverge_img = make_image_data(RealMin, RealMax, ImgMin, ImgMax, Divide)
    print(f"total time {time.time()-start} sec\n")
    diverge_img = np.log(diverge_img)  # 図の色使いを派手にするためデータのダイナミックレンジを小さく
    show_image(RealMin, RealMax, ImgMin, ImgMax, diverge_img)

このコードをファイルに保存して実行すれば、オリジナルより相当早くテトレーションフラクタルのイメージが描写できると思います。

結果

私のPCではイメージデータの作成に要する時間が0.69秒でした。マルチプロセッシングによる高速化と比較してさらに 3.3 倍の高速化が図れました。オリジナルとの比較では 12.6 倍の高速化が図れました。

補足

Numba による高速化

python の高速化テクニックに numba があります。これは cython と同様にプログラムの一部を静的な実行ファイル(JIT)にすることで高速化を図る手法です。
cython とnumba のどちらが速いかというとケースバイケースです。私のPCでマルチプロセッシングによって高速化を図ったプロブラムの実行時間は2.3秒で、cython化の実行時間は0.69秒でした。cython に替えて numba も試みたのですが、結果は1.2秒止まりでした。一方でネットでは numba のほうが早いという事例もたくさんあります。
numba の利点は、コードにたった2行を追加するだけで高速化ができるという圧倒的な簡便さです。( numba を使うための import 文と、コンパイルする関数の前hへのデコレータの2行)
マルチプロセッシング + numba による高速化を図ったプログラムは下記です。オリジナルのコード(tetration.py)との違いは、①〜⑦ の7行だけです。 numba は cython より遅かったですが、手数が圧倒的に少ないので、ある意味こちらのほうが良い手段だと言えるかもしれません。

tetration_poolmap_numba.py

import matplotlib.pyplot as plt
import multiprocessing as mp  # マルチプロセッシングを使うための import 文  ①
import numpy as np
import time
from numba import jit, int32, complex128   # numba を使うための import 文   ⑥

####  最初に各種パラメーターを設定します ###
## どの領域の複素数 z を計算するのか ##
RealMin = -2.0    # 実数部の最小値
RealMax = 2.0     # 実数部の最大値
ImgMin = -2.0     # 虚数部の最小値
ImgMax = 2.0      # 虚数部の最大値
Divide = 401      # 計算する領域で、実数軸・虚数軸をいくつに区切るか. 始点と終点を含む
## グラフのパラメーター ##
LazyInf = 200   # z のべき演算を LazyInf 回繰り返して発散しなければ、∞回でも収束するとみなす
GWidth = 10     # matplotlib で描く図の幅
GHeight = 10    # matplotlib で描く図の高さ
Colormap = "gist_heat_r" # 図の色使い。 "magma"  "cool"  "Reds" "viridis" などお好みで選んで

## @jit(<戻り値の型>(<引数の型>)) というデコレータを書くだけで numba が使える。 超簡単!!  ⑦
@jit(int32(complex128))
def check_diverge(z):
    tet = 1.0    # テトレーション演算の途中結果を格納する変数
    for n in range(LazyInf+1):
        try:
            tet = z ** tet
            if abs(tet-z) > 1000000000:  # 途中が大きな数になったら、発散するとみなす
                break
        except:
            break   # エラーが発生したら、発散するとみなす
    return(n)  # 途中で発散したら何回目で発散したかが返る。発散しなかったら LazyInf が返る。

def make_image_data(r_min, r_max, i_min, i_max, divide):
    check_diverge_processes = mp.Pool(mp.cpu_count())  # ②
    x = np.linspace(r_min, r_max, divide)       # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, divide)       # 計算する z の虚数部を格納する配列
    zs = [complex(x[r_index], y[i_index]) \
        for i_index in range(divide) for r_index in range(divide)]  # ③
    ns = check_diverge_processes.map(check_diverge, zs)  # ④
    img = np.array(ns, dtype=np.int32).reshape(divide, divide)   # ⑤
    return(img)

def show_image(r_min, r_max, i_min, i_max, img):
    fig, ax = plt.subplots(figsize=(GWidth, GHeight))
    x = np.linspace(r_min, r_max, img.shape[1])    # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, img.shape[0])    # 計算する z の虚数部を格納する配列
    X,Y = np.meshgrid(x, y)
    ax.pcolormesh(X, Y, img, cmap=Colormap)
    ax.set_xlabel("Real", fontsize=GWidth*1.5)
    ax.set_ylabel("Imaginary", fontsize=GWidth*1.5)
    plt.show()

if __name__ == "__main__":
    start = time.time()
    diverge_img = make_image_data(RealMin, RealMax, ImgMin, ImgMax, Divide)
    print(f"total time {time.time()-start} sec\n")
    diverge_img = np.log(diverge_img)  # 図の色使いを派手にするためデータのダイナミックレンジを小さく
    show_image(RealMin, RealMax, ImgMin, ImgMax, diverge_img)