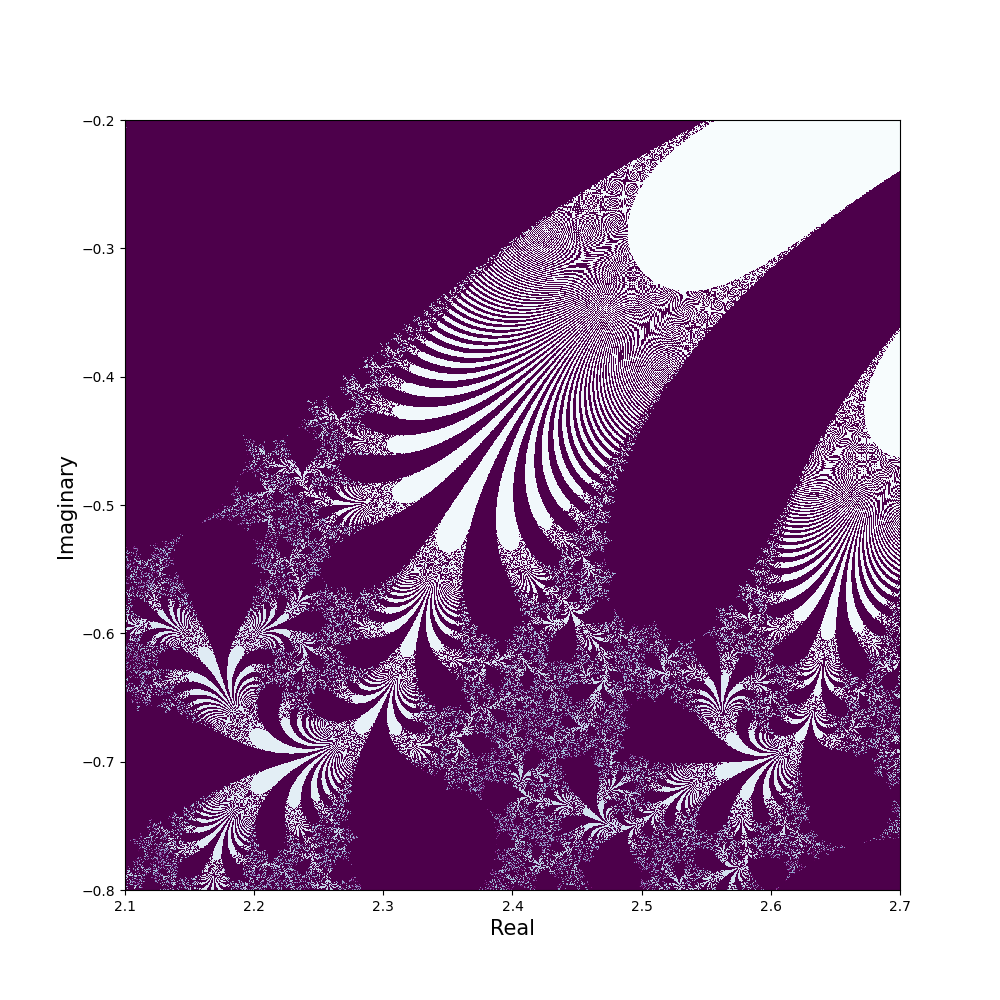
テトレーションカオスと戯れる

ギャラリー

まずはテトレーションカオスを可視化した図をご覧ください

使用言語

この記事では以降、 python と IPython をメインで使用します。理由はテトレーションカオスの可視化するときのライブラリに matplotlib が最も適していると考えたからです。私の母語はRubyなのですが、こういうライブラリは python が充実してますね。とはいえ、Ruby でも PyCall などのラッパーから matplotlib が使えますし、他の言語でも matplotlib を使う手段があると思いますので、皆様お好みの言語でテトレーションカオスと戯れてみてください。

テトレーションって何？

テトレーションとは、自らのべき乗を指定回数繰り返す演算のことです。テトレーションの表記方法は統一されてないのですが、この文章では演算子として ↑↑ を使った表記を採用し、ある数 z に対するテトレーションを、

z ↑↑ n = \left. z ^  {z^  {... \; ^ {z}}} \right\} \; n 個の\;z\;へのべき演算、べきは右から左向きに計算する 

と表記します。
たとえば、2 ↑↑ 4 は 4つの 2 にべき演算を繰り返すことの表記です。

 2 ↑↑ 4 = \left. 2 ^  {2^  {2 ^ {2}}} \right\} 4つの\; 2 \; へのべき演算

右から左向きに計算するので、
$$ 2 ↑↑ 4 = 2 ^ {2^{2^2}} = 2 ^ {2 ^ 4} = 2 ^ {16} = 65536 $$
となります。
プログラム言語で z ↑↑ n を計算する関数を実装すると次のような感じになります。

# Python
def tetration(z, n):
  ret = 1
  for i in range(1, n + 1):
    ret = z ** ret
  return ret

# Ruby
def tetration(z, n)  
  ret = 1
  n.times{ret = z ** ret}
  ret
end

# PARI/GP
tetration(z,n) = { my(ret=1); for(i=1, n, ret=z^ret); ret; }

べき演算を繰り返すのですから、 z と n を少し大きくするだけで z ↑↑ n は巨大な数になりそうです。IPythonでちょっと試してみましょう。

In : tetration(4, 3)    # 4↑↑3 
Out: 13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096   #(154桁)

In : tetration(5, 3)    # 5↑↑3
Out: 1911012597945477520356404559703964599198081048990094337139512789246520530242615803012059386519739850265586440155794462235359212788673806972288410146915986602087961...
...  
66715373374248543645663782045701654593218154053548393614250664498585403307466468541890148134347714650315037954175778622811776585876941680908203125    # (2184桁)

In : tetration(3, 4)   # 3↑↑4
Out: # (いつまで経っても計算が終わらない... 　3兆6千億桁なので...)

たかだか z=3, n=4 で、もう私のPCでは計算できないくらい大きな数になりました。テトレーションは、与えるパラメーターが手で数えられる程度の数であっても極めて大きな数を返す演算なので、巨大数界隈では巨大数の入門的な演算として扱われてるようです。
さて上の例では数 z として自然数を考えたのですが、べき演算はべつに自然数だけでなく負の数、非整数、あるいは複素数に対しても行うことができるので、それぞれのテトレーションを考えることも可能です。

-1 ↑↑ n = \left. -1 ^  {-1^  {... \; ^ {-1}}} \right\} \; n個の \;-1 \; に対してべき演算を繰り返す

\sqrt2 ↑↑ n = \sqrt2 \left. ^ { \sqrt2 ^  {... \; ^ {\sqrt2}}} \right\} \; n個の \; \sqrt2 \; に対してべき演算を繰り返す

i ↑↑ n = \left. i ^  {i^ {... \; ^ i}} \right\} \;  \; n個の虚数単位 \; i \; に対してべき演算を繰り返す

ええっと、√2 の √2 乗とか虚数の虚数乗ってどうやって計算するんだっけ？
公式とか知らなくとも大丈夫、いま眼の前にある箱が計算してくれます。

z ↑↑ ∞ を考えてみる

2とか3とか10とかの数で無限回のべき演算をするとどうなるでしょうか？
まあ無限大になるでしょうねえ。無限大に大きいも小さいもないのですが、私の感覚では無限大でもものすごくヤバイ無限大(語彙力)に発散しそうな気がします。
逆に z ↑↑ ∞ が有限の値に収束する z ってあるのでしょうか？
z = 1 がすぐ思いつくと思います。 1¹=1 だから、 1 は何回べき演算をしても 1 。 1↑↑∞ = 1 です。 -1 もそうです。 -1^-1 = 1 /(-1) = -1 だから -1 は何回べき演算しても -1。-1↑↑∞ = -1 です。
ほかにも無限にべき演算を繰り返しても無限大に発散しないような数はあるでしょうか？ 1 よりも少し大きいくらいの数なら発散しないかも。

眼の前にある箱で試してみましょう。コンソールか jupyter notebook で IPython を立ち上げてもいいですし、ブラウザでGoogle が 提供する Colab を利用していただいても結構です。Colab なら IPython の利用環境を持っておられない方でも今すぐに試すことができます。(すいません、IPython や Colabの使い方は省略いたします)
上で触れた、√2↑↑n を試します。次のコードを IPython や Colab にコピペして実行してみましょう。

def tetration(z, n):      # tetration 関数の定義
    ret = 1
    for i in range(1, n + 1):
        ret = z ** ret
    return ret

from math import sqrt     # ルートを計算する関数 sqrt をインポート
for n in [1, 2, 4, 8, 16, 32, 64, 128, 999999]:  # n=1,2,4,...に対して、
    print(tetration(sqrt(2), n))                   # √2↑↑n を計算 

Out:
1.4142135623730951
1.632526919438153
1.8409108692910108
1.9656648865173194
1.9982034775087025
1.9999949043349452
1.9999999999589224
2.0000000000000004
2.0000000000000004

2 に収束しました。
(こんな計算で √2↑↑∞ = 2 (ドヤァ)という雑な主張をすると数学のテストは0点ですが、そういうことにしておいてください。)

虚数単位 i に対しても i↑↑∞ を計算しましょう。python は複素数を (実数部+虚数部j) と表記します。虚数単位は i ではなく 1j と表記します。

for n in [1, 2, 4, 8, 16, 32, 64, 128, 999999]:
    print(tetration(1j, n))           # i↑↑n を計算

Out:
1j
(0.20787957635076193+0j)
(0.05009223610932119+0.6021165270360038j)
(0.5197863964078542+0.11838419641581431j)
(0.40063349486673666+0.26312021335073466j)
(0.42180189977625804+0.36636420976957473j)
(0.43870545626497576+0.3604591075652719j)
(0.4382832143015192+0.36059240780602697j)
(0.43828293672703206+0.3605924718713856j)

(0.43828293672703206 + 0.3605924718713856j) という数に収束するようです。

z ↑↑ ∞ の収束条件

z↑↑∞ が発散しない z がいくつかありました。では発散・収束の条件は何でしょう？ 案ずるより産むが易し。z を実数部・虚数部それぞれ -2 から 2 の間で変化させてみて、無限大のテトレーションが収束する z を探す次のコードを実行しましょう。

tetration.py

####  最初に各種パラメーターを設定します ###
## どの領域の複素数 z を計算するのか ##
RealMin = -2.0    # 実数部の最小値
RealMax = 2.0     # 実数部の最大値
ImgMin = -2.0     # 虚数部の最小値
ImgMax = 2.0      # 虚数部の最大値
Divide = 401      # 計算する領域で、実数軸・虚数軸をいくつに区切るか. 始点と終点を含む
## グラフのパラメーター ##
LazyInf = 200   # z のべき演算を LazyInf 回繰り返して発散しなければ、∞回でも収束するとみなす
GWidth = 10     # matplotlib で描く図の幅
GHeight = 10    # matplotlib で描く図の高さ
Colormap = "gist_heat_r" # 図の色使い。 "magma"  "cool"  "Reds" "viridis" などお好みで選んで

import matplotlib.pyplot as plt
import numpy as np

def check_diverge(z):
    """ z↑↑n の計算で n が有限の値で発散するかをチェックする。最大 z↑↑LazyInf まで調べる。
    """
    tet = 1.0    # テトレーション演算の途中結果を格納する変数
    for n in range(LazyInf+1):
        try:
            tet = z ** tet
            if abs(tet-z) > 1000000000:  # 途中が大きな数になったら、発散するとみなす
                break
        except:
            break   # エラーが発生したら、発散するとみなす
    return(n)   # 途中で発散したら何回目の計算で発散したかが返る。発散しなかったら LazyInf が返る。

def make_image_data(r_min, r_max, i_min, i_max, divide):
    """ 指定された領域を実数部、虚数部ともに divide 個に分割した numpy の配列を作り、
        z↑↑n が n がいくつで発散するかを格納する。
    """
    x = np.linspace(r_min, r_max, divide)              # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, divide)              # 計算する z の虚数部を格納する配列
    img = np.zeros((y.size, x.size), dtype=np.int32)   # n がいくつで発散するかを格納する配列
    for i_index in range(y.size):
        for r_index in range(x.size):
            img[i_index, r_index] = check_diverge(complex(x[r_index], y[i_index]))
    return(img)

def show_image(r_min, r_max, i_min, i_max, img):
    """ matplotlib の pcolormesh を使って結果を図にする。"""
    fig, ax = plt.subplots(figsize=(GWidth, GHeight))
    x = np.linspace(r_min, r_max, img.shape[1])              # 計算する z の実数部を格納する配列
    y = np.linspace(i_min, i_max, img.shape[0])              # 計算する z の虚数部を格納する配列
    X,Y = np.meshgrid(x, y)
    ax.pcolormesh(X, Y, img, cmap=Colormap)
    ax.set_xlabel("Real", fontsize=GWidth*1.5)
    ax.set_ylabel("Imaginary", fontsize=GWidth*1.5)
    plt.show()

diverge_img = make_image_data(RealMin, RealMax, ImgMin, ImgMax, Divide)
diverge_img = np.log(diverge_img)  # 図の色使いを派手にするためデータのダイナミックレンジを小さく
show_image(RealMin, RealMax, ImgMin, ImgMax, diverge_img)

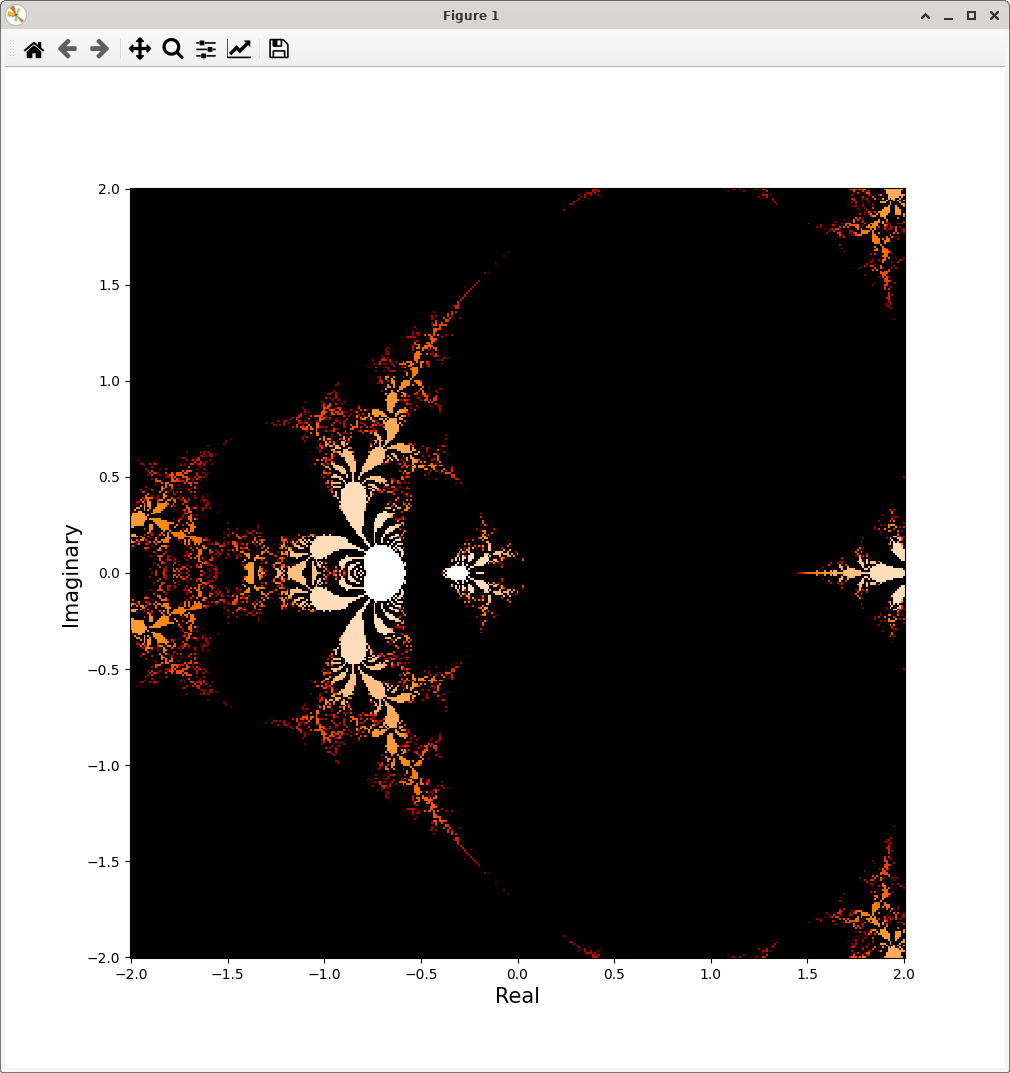
このような図が得られたと思います。
図の色使いは、z がすぐ発散するときは白、発散するときの n が 6 くらいから大きくなるにつれて暗い赤になって行き、n=LazyInf でも発散しないとき(収束するとき)は黒です。z↑↑∞ って意外と収束する z が多いように感じませんか？ 発散・収束の条件は、なんとなくいくつかのパターンが大きさを変えて組み合わさっているように見えます。フラクタル構造です。
発散・収束が入り乱れている、-0.75-1j のあたりを拡大して見てみましょう。計算範囲を変えた次のコードをコピペして実行してみてください。

RealMin = -1.0     # 実数部の最小値
RealMax = -0.5     # 実数部の最大値
ImgMin = -1.25     # 虚数部の最小値
ImgMax = -0.75     # 虚数部の最大値
diverge_img = make_image_data(RealMin, RealMax, ImgMin, ImgMax, Divide)
diverge_img = np.log(diverge_img)
show_image(RealMin, RealMax, ImgMin, ImgMax, diverge_img)

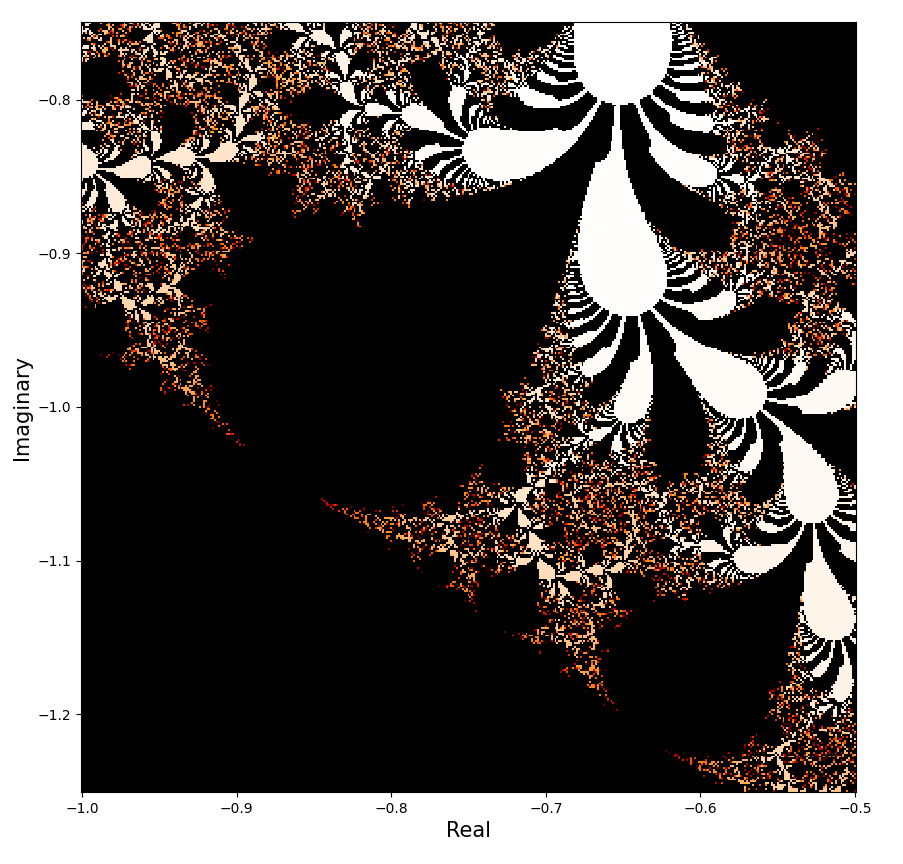
おお、なんかフラクタル性がさっきよりよく見えてきました。
範囲、色使い、範囲の分割数を色々変えると他にも面白い景色が見えてきます。
ギャラリーの図もそのようにして描いたものです。

計算の精度と z ↑↑ n の収束

python の複素数はそれぞれ24バイトの float で表される実数部と虚数部によって保持されています。通常はこれだけの精度があれば困ることはないのですが、テトレーション演算には十分ではありません。z ↑↑ 200 が有限の数 a に収束するかどうかは上に挙たプログラムでは判定ミスが多少はあると思いますし、a の計算値なんかは全然信用できないです。
できるだけ正確な計算をしたいとか、pythonの計算値がだいたい合っていそうかをチェックするには任意精度の計算ができるソフトが有益です。任意精度の計算をする商用ソフトは mathematica 、フリーソフトでは PARI/GP が定番でしょう。テトレーションカオスと戯れる際、なんか結果がおかしいなと思ったら、高精度の計算でチェックしてみましょう。

高速化

テトレーションカオスと戯れる 2 - 高速化編 をご参照ください。10倍以上の高速化が可能です。

そのほかのテトレーションカオス

この記事では、z↑↑∞ の発散と収束のフラクタル性を取り上げましたが、z↑↑∞ がどこに収束するかとか、z↑↑n がどのような軌道を描くかとかもカオスです。テトレーションにはいくつものカオスが隠れているようです。

リンク

私が複素数のテトレーションという概念を初めて知った妖精さんのサイトの記事。
Paul Bourke さんによるテトレーションカオスの紹介 (英語)
テトレーションフォーラム