1. はじめに
はじめまして!高校 2 年生の square1001 です。
私は主に「競技プログラミング」に取り組んでいます。情報オリンピックの世界大会の日本代表になったり、TopCoder や AtCoder などのプログラミングコンテストにも出場したりしています。コンテストに出場するだけでなく、問題の作成も積極的にやっています。
ところで、みなさんは、「日本数学オリンピック」という大会を知っていますか?これは、日本全国の高校生以下を対象にした、数学の問題解決能力を競う、**全国的にとても有名な大会です。**本記事では、日本数学オリンピックの予選で出題される問題を、難しい数学的知識や数学的考察を使わずに、「コンピューターの高い計算能力」と「アルゴリズムの力」でチャレンジしてみます!
導入 - コンピューターが世界を変えた!
プログラミングを実務などでやっている方の中には、「システムやアプリケーションを実現する」ための道具としてプログラミングがある、と思っている方も多いかもしれません。
しかし、プログラミングには別の側面として、「コンピューターの高い計算能力」と「アルゴリズムの力」を組み合わせて、問題を効率的に解くという側面もあります。例えば、
- 地図上の 2 つの地点の間を自動車で移動するのに何分かかる?
- 検索した文字列に対して、一番マッチしているウェブサイトは?
- 今持っているコインだけで、$X$ 円をちょうど支払えるか?
- 結婚したい男女のペアのリストが分かっているとき、最大で何組のカップルの結婚を実現させられるか?
- $10^{20}$ 以下の素数はいくつあるか?
上に挙げた問題は、コンピューターによる計算を使ってこそ解ける問題なのです!
コンピューターの力を借りることができなかった時代、人間だけの計算では、上に挙げたような問題を解くことがとても難しかったです。例えば、現在になっては 31 兆桁(!)1 も計算されている円周率も、コンピューターがなかった 19 世紀は、William Shanks という人が円周率を 527 桁求めるのに 15 年もかかった、というのは有名な話です。
これだけ「コンピューターの計算能力」と、これに伴った「アルゴリズムの力」が、世界を変えたのです!
今回解く数学オリンピックの問題
今回の記事では、2019 年日本数学オリンピック予選 の問題をプログラミングで解いてみます。
もちろん、数学オリンピック本番ではパソコンを使うことは禁止されているので、プログラミングは使えません! ですので、注意ですが、数学オリンピック対策目的でこの記事を読まないでください。
ぜひみなさんに、問題を解いていくという側面で、コンピューター・プログラミングがいかに強大な力を発揮することができるのかを、実感してくれればと思います!
2. 実際に問題を解いてみる!
これから解く 12 問は、このページ で見ることができます。
1 問ごとに、プログラミングを用いてどのように解いたのかを説明していきます。難しい数学的考察や数学的知識なしの縛りで解くので、気軽に読んでいってください。
2-0. 読んでいく上での前提
現代のコンピューターは,$1$ 秒に $10^8$ 回から $10^9$ 回程度の計算ができるといわれています。
今から挙げる問題を解いていく際に、全探索などをする場面とかがあるので、これを少し意識しながら読んでいってください。
計算量とプログラムの実行時間についてもっと詳しく知りたい方は、以下の記事を読むと良いです。
2-1. 問題 1
以下、問題文を書いておきます。
正の整数の組 $(x, y, z)$ であって,$x + xy + xyz = 31$,$x < y < z$ となるものをすべて求めよ.
明らかに、$1 \leq x \leq 31, 1 \leq y \leq 31, 1 \leq z \leq 31$ です。これで候補は $31^3 = 29,791$ 通りとなるので、これをコンピューターの力で全探索すれば解けます。
以下は、Python 3 で実装したプログラムになります。
n = 31
for x in range(1, n + 1):
for y in range(x + 1, n + 1):
for z in range(y + 1, n + 1):
if x + x * y + x * y * z == n:
print("(x, y, z) = ({0}, {1}, {2})".format(x, y, z))
実行すると、以下のように出力されます。
(x, y, z) = (1, 2, 14)
(x, y, z) = (1, 3, 9)
これで、問題 1 を解くことができました!
2-2. 問題 2
以下、問題文を書いておきます。
どの桁も素数であるような正の整数を「良い数」という.$3$ 桁の良い数であって,$2$ 乗すると $5$ 桁の良い数になるものをすべて求めよ.
一桁の素数は $2, 3, 5, 7$ だけですから、「良い数」な条件はどの桁も $2, 3, 5, 7$ のうちいずれかである,ということです。例えば、$527337$ とかは良い数になります。
ですので、$N$ が「良い数」であるかは、まず $N$ を文字列に直して、その中のどの文字も '2', '3', '5, '7' のいずれかであるかどうかで判定することができます。
$3$ 桁の正の整数は $900$ 個 ($100$ から $999$ まで) しかないので,あとはこれが
一つ一つ条件を満たしているか判定するだけです。人間にとっては $900$ 個は厳しいですが、コンピューターにとっては楽勝です。
以下は、Python 3 で実装したプログラムになります。
def is_nice(n, target_len):
s = str(n)
if len(s) != target_len:
return False
for i in s:
if i != '2' and i != '3' and i != '5' and i != '7':
return False
return True
for n in range(100, 1000):
if is_nice(n, 3) and is_nice(n * n, 5):
print(n)
出力結果は 235 となりますので、条件を満たす数は $235$ だけであることがわかりました!
これで簡単に問題 2 も解いてしまいました。
2-3. 問題 3
以下、問題文を書いておきます。
$3 \times 3$ のマス目の各マスに $1$ 以上 $9$ 以下の整数が重複しないように $1$ つずつ書き込む.辺を共有して隣り合うどの $3$ マスについても書き込まれた $2$ マスも書き込まれた整数の差が $3$ 以下にように書き込む方法は何通りあるか.
ただし,回転や裏返しにより一致する書き込み方も異なるものとして数える.
以下、条件を満たす書き込み方の例と条件を満たさない書き込み方の例です。
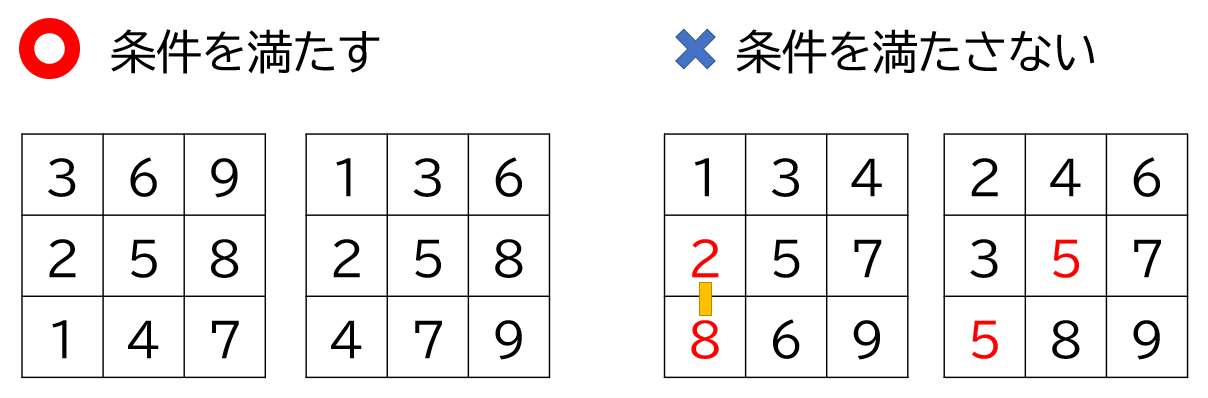
条件を満たすマス目は、$1, 2, 3, 4, 5, 6, 7, 8, 9$ がひとつずつ出てきます。このような方法は「$1$ から $9$ までを並び替える方法の数」だけ、つまり $9! = 362 \ 880$ 通りの候補があります。このくらいだったら、コンピューターを使うと全探索することができます。
以下は、Python 3 で実装したプログラムになります。Python 3 には、順列をすべて生成する関数 itertools.permutations があるので、比較的楽に実装できます。
import itertools
seq = [ 1, 2, 3, 4, 5, 6, 7, 8, 9 ]
candidates = list(itertools.permutations(seq)) # これで 1~9 の順列をすべて生成!
answers = 0
for v in candidates:
# v はマス目の状態の候補 (上図の一番左の例だと [3, 6, 9, 2, 5, 8, 1, 4, 7])
ok = True
for i in range(0, 9):
if i % 3 != 2 and abs(v[i] - v[i + 1]) >= 4:
ok = False
if i <= 5 and abs(v[i] - v[i + 3]) >= 4:
ok = False
if ok:
print("v = {0}".format(v))
answers += 1
print("Answer: {0}".format(answers))
出力結果は以下のようになり、たった $1$~$2$ 秒の実行で、答えである「$32$ 通り」が求まりました!
v = (1, 2, 3, 4, 5, 6, 7, 8, 9)
v = (1, 2, 4, 3, 5, 7, 6, 8, 9)
v = (1, 3, 2, 4, 6, 5, 7, 9, 8)
: : :
v = (9, 8, 7, 6, 5, 4, 3, 2, 1)
Answer: 32
2-4. 問題 4
ついに数学オリンピックの難関、「初等幾何」の問題の登場です!以下、問題文を書いておきます。
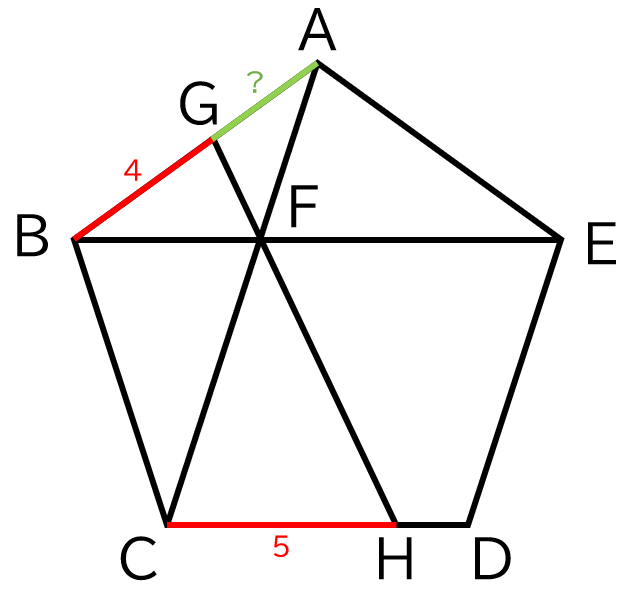
正五角形 $ABCDE$ があり,線分 $BE$ と線分 $AC$ の交点を $F$ とする.また点 $F$ を通る直線が辺 $AB$,$CD$ とそれぞれ点 $G, H$ で交わり,$BG = 4$,$CH = 5$ が成り立つ.このとき線分 $AG$ の長さを求めよ.ただし,$XY$ で線分 $XY$ の長さを表すものとする.
つまり、下のような図での $AG$ の長さを求める、といった問題です。
実は、**幾何的な問題もプログラミングを使うと数値的に解けることがあります!**だからこそ、実務でもプログラミングを用いて 3D モデルなどを処理することがあるとか。
しかし、今の時点では、正五角形の一辺の長さすら分かっていません!ですので、どこから手を付ければよいのでしょうか?
ここで、正五角形の大きさを決め打ちして、実際これより大きいか小さいかを求めて、探索範囲を狭めていくという方法を考えてみましょう!
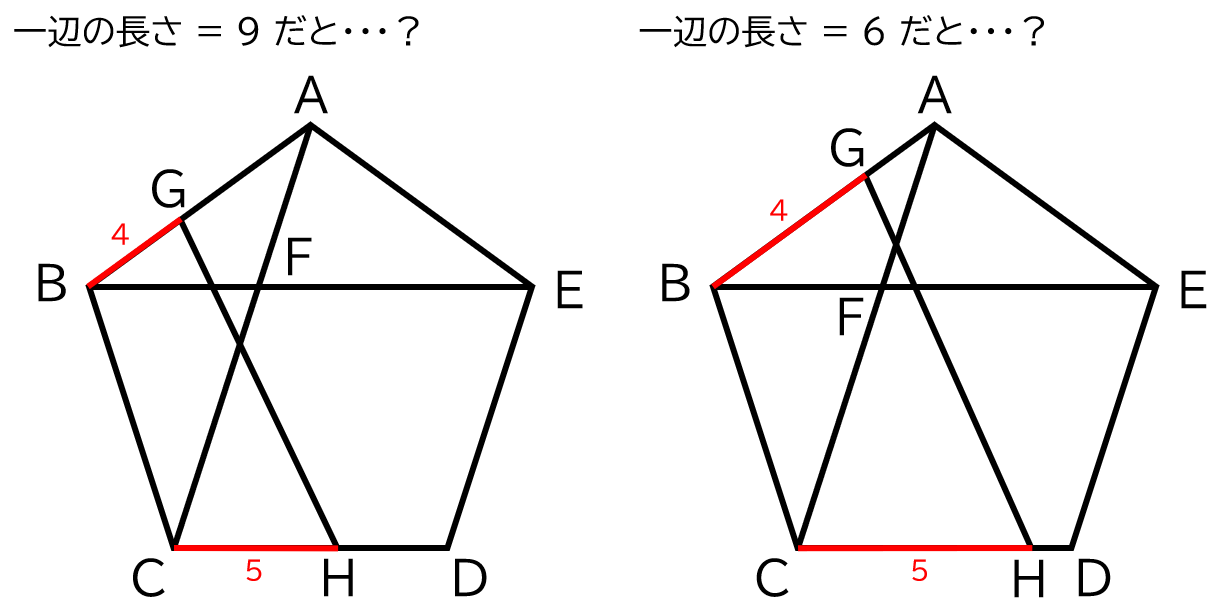
- 例えば、一辺の長さが $6$ だと、線分 $GH$ が $F$ より下に来るので、実際は一辺の長さは $6$ より大きい!
- 例えば、一辺の長さが $9$ だと、線分 $GH$ が $F$ より上に来るので、実際は一辺の長さは $9$ より小さい!
一辺の長さが分かっていれば、各点の座標も数値的に求めることができます。これで、$X$ が入力されたとき、「正五角形の一辺の長さが $X$ より大きいかどうか」を判定するプログラムが書けます!
すると、あとは実際の一辺の長さを二分探索によって求めることができます!
「二分探索」は、以下のようなイメージのアルゴリズムです。
1. 一辺の長さは明らかに 5 以上なので、例えば 5~125 と適当に見積もって L = 5, R = 15 と見積もる
2. M = (L + R) / 2 する
3. もし「一辺の長さが M より大きい」なら次の R を M にする
4. もし「一辺の長さが M より小さい」なら次の L を M にする
5. 2. ~ 4. を、R-L が十分小さくなるまで繰り返す
実際にやってみると、以下の表のように動作します。
| $L$ | $R$ | $M$ | 判定 |
|---|---|---|---|
| 5 | 15 | 10 | 一辺の長さは 10 より小さい! |
| 5 | 10 | 7.5 | 一辺の長さは 7.5 より小さい! |
| 5 | 7.5 | 6.25 | 一辺の長さは 6.25 より大きい! |
| 6.25 | 7.5 | 6.875 | 一辺の長さは 6.875 より大きい! |
| : | : | : | : |
このようにして、「答えの範囲」は最初の 1/2, 1/4, 1/8, 1/16,... になっていき、50 回程度の繰り返しで十分な精度の答えを求めることができます!
以下は、Python 3 で実装したプログラムになります。
import math
L = 5.0; R = 15.0
golden_ratio = (1 + math.sqrt(5)) / 2
for i in range(58):
M = (L + R) / 2
# C(0, 0)、D(M, 0) として各点の座標を計算
Bx = M * math.cos(108 / 180 * math.pi); By = M * math.sin(108 / 180 * math.pi)
Fx = -Bx; Fy = By
Gx = Bx + 4 * math.cos(36 / 180 * math.pi); Gy = By + 4 * math.sin(36 / 180 * math.pi)
Hx = 5; Hy = 0
if (Fx - Gx) * (Hy - Gy) - (Fy - Gy) * (Hx - Gx) < 0:
R = M
else:
L = M
print("Answer: {0}".format(L))
実行すると、Answer: 6.8989794855663575 のように出力されますから、一辺の長さが $2\sqrt{6} + 2$ であることは推測がつくでしょう。よって、答えである $AG$ の長さは $2\sqrt{6} - 2$ と分かります。
2-5. 問題 5
以下、問題文を書いておきます。
$97, 100, 103$ で割った余りがそれぞれ $32, 33, 34$ である正の整数のうち最小のものを求めよ.
実際に数学オリンピックでこの問題を解いたときは、うまい性質を見つけなければなりませんでした。しかし、コンピューターの力を使うと、こんな問題なんて一瞬です!
次のような方法で、答えが求まります。
- $1$ は OK か? → $97, 100, 103$ で割った余りが $1, 1, 1$ なので NG
- $2$ は OK か? → $97, 100, 103$ で割った余りが $2, 2, 2$ なので NG
- $3$ は OK か? → $97, 100, 103$ で割った余りが $3, 3, 3$ なので NG
- (中略)
- $10000$ は OK か? → $97, 100, 103$ で割った余りが $9, 0, 9$ なので NG
- (中略)
- $333033$ は OK か? → $97, 100, 103$ で割った余りが $32, 33, 34$ なので OK!!!
要するに、$1, 2, 3, ...$ の順に「$97, 100, 103$ で割った余りがそれぞれ $32, 33, 34$ かどうか」を判定して、見つかったらプログラムを終了させればよいです。2
答えは 333033 と、コンピューターにとっては小さな数なので、すぐに答えが求まります!
以下は、Python 3 で実装したプログラムになります。
n = 1
while n % 97 != 32 or n % 100 != 33 or n % 103 != 34:
n += 1
print("Answer: {0}".format(n))
2-6. 問題 6
以下、問題文を書いておきます。
正 $120$ 角形のいくつかの頂点に印がついている.印のついた $3$ つの頂点の組であって,頂角が $18°$ の二等辺三角形の $3$ 頂点をなすものが存在しないとき,印のついた頂点の個数としてありうる最大値を求めよ.
正 $120$ 角形の頂点を $0, 1, 2, 3, ..., 119$ と時計回りに番号づけることを考えましょう。すると、頂角が $18°$ の二等辺三角形をなす点の組は、$(0, 54, 66)$,$(1, 55, 67)$,$(2, 56, 68)$,$(3, 57, 69)$,... などがあります.
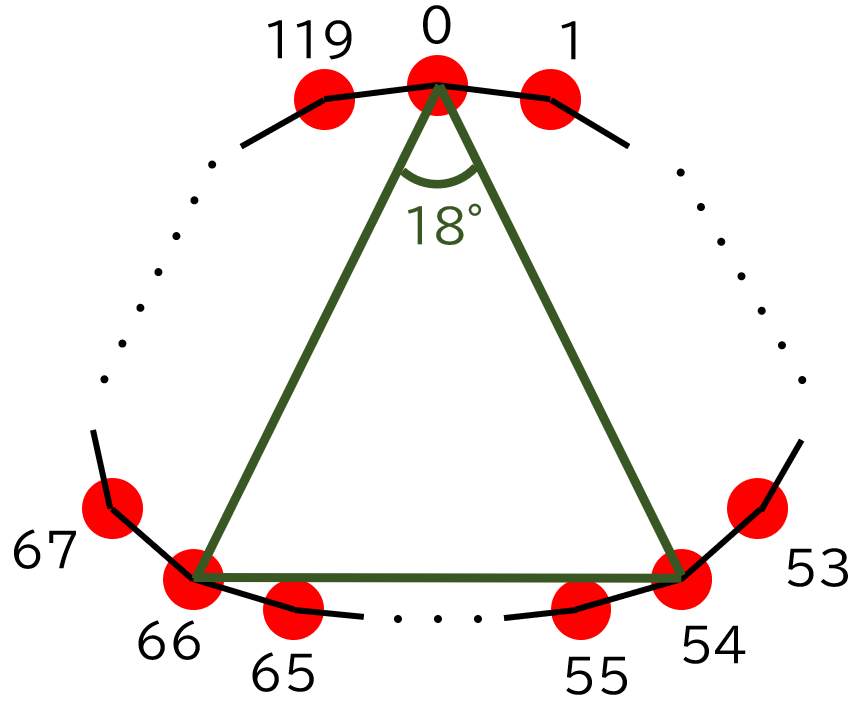
これは,幾何の知識を使って見つけることもできますが,$3$ 点の選び方は $_{120}C_3 = 280 \ 840$ 通りしかないので,コンピューターで全探索してもよさそうです。
これによって,頂角が $18°$ の二等辺三角形の $3$ つの頂点番号は i, (i+54)%120, (i+66)%120 のように表せることがわかります。これより 「頂角が $18°$ の二等辺三角形」の頂点番号を $6$ で割った余りは全部同じ であることが分かります!
だから、例えば「番号 $5$ の頂点に印がつけられているか」は「番号 $12$ の頂点に印がつけられているか」には直接的にも間接的にも関係ありません!
したがって、「番号 $0, 6, 12, \dots, 114$ の頂点のグループ」「番号 $1, 7, 13, \dots, 115$ の頂点のグループ」・・・「番号 $5, 11, 17, \dots, 119$ の頂点のグループ」の $6$ つに分けて考えることができます。
ここでなんと!$6$ つのうちどのグループの頂点の数も $20$ 個です!競技プログラミングをやっている人は、「$N \leq 20$」という制約に見覚えがあるかもしれません。そう!$2^N$ 通り全探索です!
それぞれの頂点は「印をつけるかつけないか」の $2$ 通りです。各グループには $20$ 個の頂点があるので、グループの「印のつけ方」は $2^{20} = 1 \ 048 \ 576$ 通りしかありません!
先ほど書いたことを思い出してください。コンピューターは $1$ 秒に $10^9$ 回程度の計算ができます。ですので、$1 \ 048 \ 576$ 通り全探索しても高々数秒しか実行にかからないと思えます。
さあ,実際にコードを書いてみましょう!
以下は、Python 3 で実装したプログラムになります。
ans = 0
for i in range(2**20):
A = []
x = i
for j in range(20):
A.append(x % 2)
x //= 2
# A[k] = 1 なら番号 6k の頂点は印をつけられている
ok = True
for j in range(20):
if A[j] == 1 and A[(j+9)%20] == 1 and A[(j+11)%20] == 1:
ok = False
break
if ok:
cnt = 0
for j in range(20):
cnt += A[j]
ans = max(ans, cnt)
print("Answer: {0}".format(ans))
数秒の実行で Answer: 13 と出ました。これで、「頂点 $0, 6, 12, \dots, 114$ のグループ」では、最大で $13$ 個の印がつけられることが分かりました。他のグループでも同じなので、最大で $13 \times 6 = 78$ 個の印がつけられるのが分かります。
2-7. 問題 7
今回解き方を解説(?)する問題の中で、おそらくこれが一番 (解き方的には) 複雑だと思います。
以下、問題文を書いておきます。
整数係数 $2$ 次多項式 $P(x), Q(x), R(x)$ は以下の条件を満たすとする.このとき $R(x)$ として考えられるものをすべて求めよ.
- $P(1) = P(2) = Q(3) = 0$
- 任意の実数 $x$ に対して $P(x)^2 + Q(x)^2 = R(x)^2$ が成り立つ.
- $P, Q, R$ のすべての係数を割り切る $2$ 以上の整数はない.
- $P, Q$ の $2$ 次の係数は $0$ ではなく,$R$ の $2$ 次の係数は正である.
一番目、三番目、四番目の条件から、$P(x), Q(x)$ は次のように表されることがわかります.
- $P(x) = a(x-1)(x-2) = ax^2 - 3ax + 2a$
- $Q(x) = b(x-3)(cx-d) = bcx^2 - (3c+d)bx + 3bd$
- ただし,$a, b$ は $0$ でない整数,$c, d$ は整数
- $a$ と $b$ の最大公約数は $1$
- $c$ と $d$ の最大公約数は $1$
残すは二番目の条件だけです!
しかし、実際に数学オリンピックでこの問題を解く際は、$a, b, c$ の値を $P(x)^2 + Q(x)^2 = R(x)^2$ を満たすように、つまり $P(x)^2 + Q(x)^2$ が「整数係数多項式の $2$ 乗」になるように、数学的な手法を用いて決定しなければなりません。
しかしこの問題は、答えさえ合えば正解です。実際、$P(x), Q(x)$ の係数が一万とか十万とかになるのは常識的に考えてありえないので、係数が大体 $\pm 100$ くらいに収まるもの絞って考えることにします。
ですので、$a, bc, bd$ が $-100$ 以上 $100$ 以下のものだけ候補にしましょう!直感的に、このような $(a, b, c, d)$ の組は数百万通りくらいしかないことは分かるでしょう。これは、コンピューターで全探索できるレベルの組み合わせの数です。(実際は $3 \ 355 \ 120$ 通りです)
以下、決め打ちした $P(x), Q(x)$ に対して、$P(x)^2 + Q(x)^2$ が「整数係数多項式 $R(x)$ の $2$ 乗」で表されるかどうかを判定するだけです。この判定もそこまで難しくないです。3
では、いざ実装です!以下は、Python 3 で実装したプログラムです。
import math
import fractions # using gcd for version < 3.5
def polynomial_add(f, g):
n = max(len(f), len(g)) - 1
a = [0] * (n + 1)
for i in range(len(f)):
a[i] += f[i]
for i in range(len(g)):
a[i] += g[i]
return a
def polynomial_square(f):
n = len(f) - 1
a = [0] * (2 * n + 1)
for i in range(n + 1):
for j in range(n + 1):
a[i + j] += f[i] * f[j]
return a
def polynomial_square_root(f):
z = len(f) - 1
if z % 2 != 0 or f[z] < 0:
return []
n = z // 2
a = [0] * (n + 1)
a[n] = int(math.sqrt(f[2 * n]))
if a[n] * a[n] != f[2 * n]:
return []
for i in range(n - 1, -1, -1):
a2 = polynomial_square(a)
rem = f[n + i] - a2[n + i]
if abs(rem) % (2 * a[n]) != 0:
return []
a[i] = rem // (2 * a[n])
if polynomial_square(a) != f:
return []
return a
X = 100
for a in range(-X, X + 1):
for b in range(-X, X + 1):
if a == 0 or b == 0 or fractions.gcd(a, b) != 1:
continue
limit = X // abs(b)
for c in range(-limit, limit + 1):
for d in range(-limit, limit + 1):
if fractions.gcd(c, d) != 1:
continue
p = [ 2 * a, -3 * a, a ]
q = [ 3 * b * d, -(3 * c + d) * b, b * c ]
p2 = polynomial_square(p)
q2 = polynomial_square(q)
r2 = polynomial_add(p2, q2)
r = polynomial_square_root(r2)
if r != []:
print("a = {0}, b = {1}, c = {2}, d = {3}, p = {4}, q = {5}, r = {6}".format(a, b, c, d, p, q, r))
すると、実行結果は以下のようになり、$R(x) = 5x^2 - 18x + 17$ のみが解になりそうなことが分かりました!
a = -4, b = 1, c = 3, d = 5, p = [-8, 12, -4], q = [15, -14, 3], r = [17, -18, 5]
a = 4, b = 1, c = 3, d = 5, p = [8, -12, 4], q = [15, -14, 3], r = [17, -18, 5]
2-9. 問題 9
「条件をみたすものは何通りあるか」という問題は、コンピューターの力を使うのと相性の良い問題が多く、競技プログラミングにおいてもたびたび出題されています。実は、この問題もコンピューターとの相性が良い問題のひとつです。
以下、問題文を書いておきます。
$4 \times 4$ のマス目の各マスを,赤,青,黄,緑のいずれか $1$ 色で塗る方法のうち,どの行と列についても,次の $3$ つの条件のうちいずれかを満たすものは何通りあるか.
- $1$ 色で $4$ 個のマスすべてを塗る.
- 異なる $2$ 色でそれぞれ $2$ 個のマスを塗る.
- $4$ 色すべてでそれぞれ $1$ 個のマスを塗る.
ただし,回転や裏返しにより一致する塗り方も異なるものとして数える.
マス目は $16$ 個のマスからなるので、これを $4$ 色のうちいずれかで塗る方法は $4^{16} = 4 \ 294 \ 967 \ 296$ 通りあります。しかし、これだとコンピューターでも相当な時間がかかってしまいます。
ここで、列ごとに考えてみましょう。
一列を塗る方法は $4^4 = 256$ 通りありますが、その中で条件を満たすものはそこまで多くないはずです。プログラムを書いて確かめてみると、$64$ 通りしかないことが分かると思います。
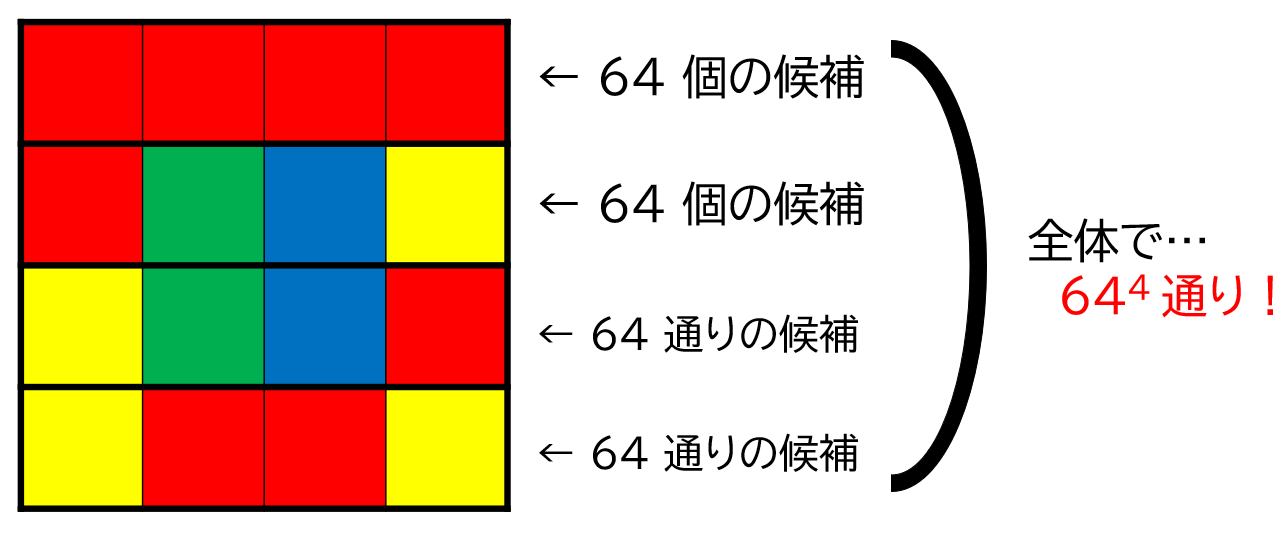
ですので、全体で $64^4 = 16 \ 777 \ 216$ 通りの候補しか探索する必要がありません!これで、現実的な計算時間で答えが求まりそうです。
このように、「フィルター」をかけて候補を絞り込むのは、コンピューターを使って問題を解いていく上で大事な一手でもあります。4 多くのチェスや将棋などの AI でも、探索範囲を絞り込む工夫が施されています。
さあ、実装をしてみましょう!ここでも Python の itertools が大活躍します!
import itertools
def is_valid_row(a, b, c, d):
cnt = [0] * 4
cnt[a] += 1; cnt[b] += 1; cnt[c] += 1; cnt[d] += 1
cnt.sort()
return (cnt == [1, 1, 1, 1] or cnt == [0, 0, 2, 2] or cnt == [0, 0, 0, 4])
valid_row = []
for a in range(0, 4):
for b in range(0, 4):
for c in range(0, 4):
for d in range(0, 4):
if is_valid_row(a, b, c, d):
valid_row.append([a, b, c, d])
valid_board = list(itertools.product(valid_row, repeat=4))
answer = 0
for board in valid_board:
ok = True
for i in range(4):
if not is_valid_row(board[0][i], board[1][i], board[2][i], board[3][i]):
ok = False
break
if ok:
answer += 1
print("Answer: {0}".format(answer))
PyPy 3 で 8 秒程度で実行できました。出力結果は Answer: 262144 なので、答えは $262,144$ 通り、正解です!
2-10. 問題 10
初等幾何の超難問です!以下、問題文を書いておきます。
三角形 $ABC$ と辺 $AB, AC$ 上の点 $D, E$ について,$AB = 6$,$AC = 9$,$AD = 4$,$AE = 6$ が成り立っている.また,三角形 $ADE$ の外接円が辺 $BC$ と $2$ 点 $F, G$ で交わっている.ただし,$4$ 点 $B, F, G, C$ はこの順に並んでいる.直線 $DF$ と $EG$ が三角形 $ABC$ の外接円上で交わるとき、$FG \div BC$ の値を求めよ.なお,$XY$ で線分 $XY$ の長さを表すものとする.
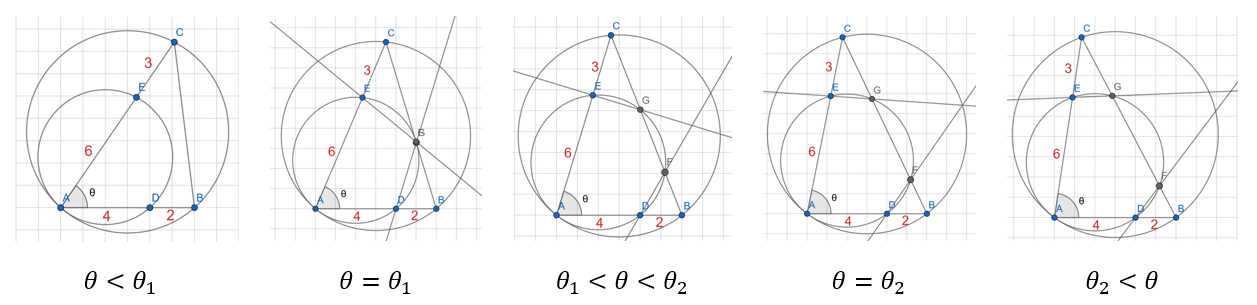
図で表すと、下のような感じになります。(Geogebra を用いて図を作成しました)
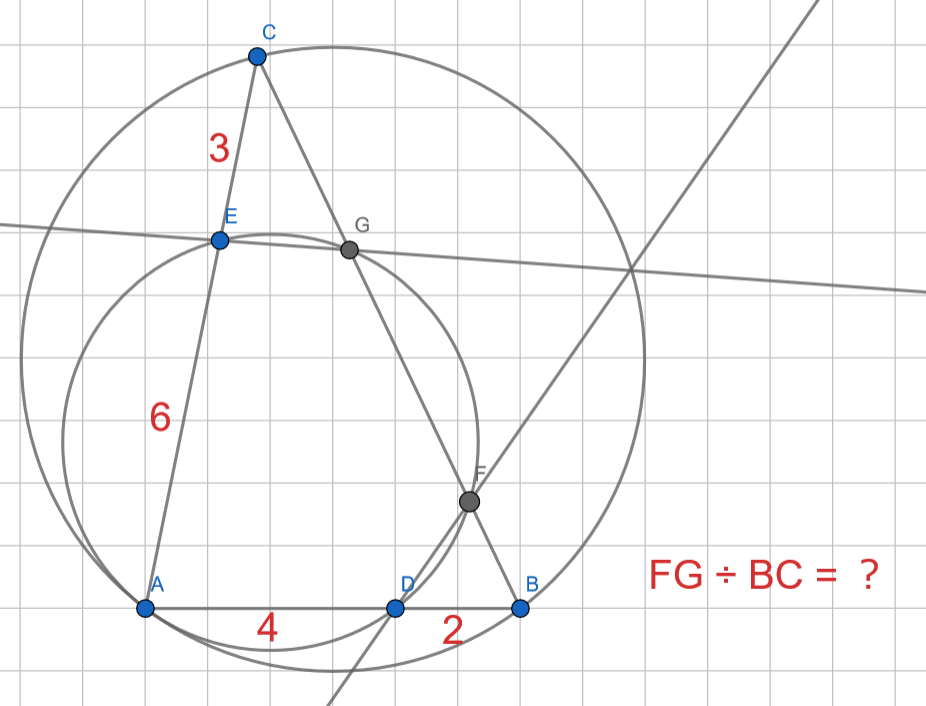
予選の 10 番となると、数学的に解こうとするととても難しい問題になります。
しかし、コンピューターを使って数値的に解けば、実はかなりシンプルに答えが出せてしまうのです!なぜなら...?
- $∠BAC = \theta$ が決まれば、点 $A, B, C, D, E, F, G$ の位置関係がすべて決まる!
ですから、$DF$ と $EG$ の交点と三角形 $ABC$ の外接円が交わるようにうまく $\theta$ を決めればよいです。より具体的には、次のようになっています。
- $\theta < \theta_1$ なら、$ADE$ の外接円と $BC$ は交わらない (つまり、点 $F, G$ は存在しない)
- $\theta = \theta_1$ なら、$ADE$ の外接円と $BC$ は一点で交わる
- $\theta_1 < \theta < \theta_2$ なら、$DF$ と $EG$ の交点は $ABC$ の外接円の内部
- $\theta = \theta_2$ なら、$DF$ と $EG$ の交点は $ABC$ の外接円上にある
- $\theta_2 < \theta$ なら、$DF$ と $EG$ の交点は $ABC$ の外接円の外部にある
もし $\theta_2$ を正確に求めることができるなら、そのまますべての点の位置を求めることができ、答えが求まります。
ここで、問題 4 と同じような感じで、$\theta_2$ という "境界線" を二分探索によって求めることができます!このようにして、この問題を解くことができるのです。
(実装プログラムは「3 点を通る円を求める」部分などが少し複雑なので、ここでは省略しておきます)
3. 結果 ~コンピューターで解ける問題の幅は広かった~
結果的に、プログラミングの力で、問題 1, 2, 3, 4, 5, 6, 7, 9, 10 を解くことができ、なんと 9 問を正解することができました!実際の数学オリンピック本番での最高点は 8 問正解なので、なんとこれを超してしまいました。
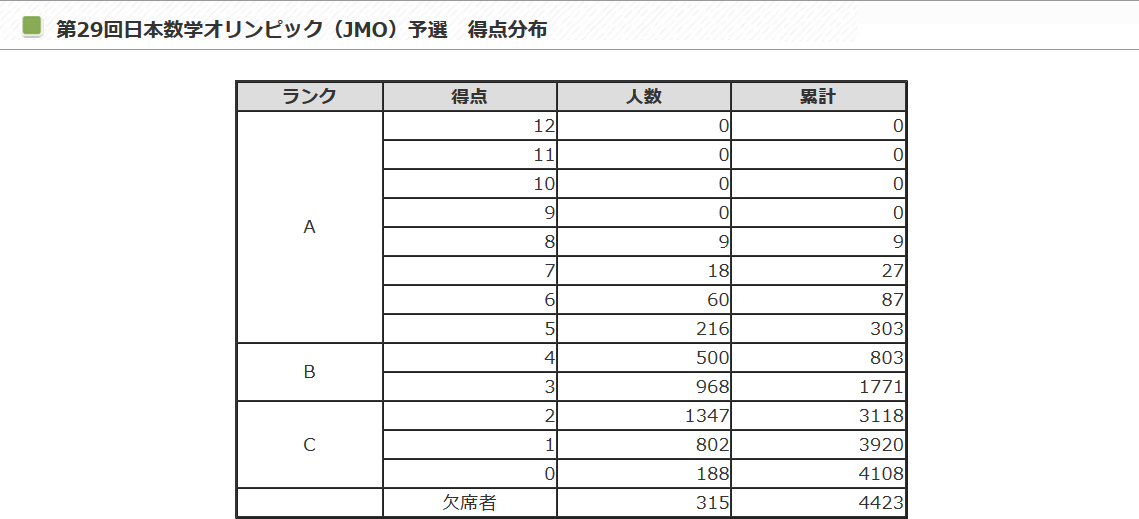
(画像は 日本数学オリンピックのページ より)
「コンピューターの高い計算能力」と「アルゴリズムの力」が組み合わさると、現実世界の問題も含め、解ける問題の幅が一気に広がります!
3-1. Project Euler をやりましょう!
この記事は面白かったですか?数学的な問題をプログラミングの力と組み合わせて解いていくのは、とても面白いですが、このような問題が解けるサイトは、実はすでにあります!
- Project Euler という世界的に有名なサイトです!
このサービスは 2001 年に始まり、毎週 1~2 問ずつ問題が増えていきます。現在、700 問近くの問題が出題されています。ちなみに私は 2020/1/20 時点で 224 問解いており、問題作成の側にも関わったことがあります。
どのような問題が出題されているのでしょうか?下がこの一例です:
次のような数列 $a_0, a_1, a_2, \dots$ がある.
- $a_0 = 1$
- $a_{n+1} =$ ($a_0, a_1, a_2, \dots, a_n$ の各桁の数字の和の合計)
これは,$1, 1, 2, 4, 8, 16, 23, 28, 38, 49, \dots$ と続きます。
数列の第 $10^{15}$ 項、すなわち $a_{10^{15}}$ を計算してください。
(Project Euler 551 - Sum of Digits Sequence より)
普通に計算しようとすると、現実的な時間で実行が終了しないので、一工夫する必要があります。ぜひ考えてみましょう!(ちなみに、これは約 700 問の中でも難しい方の問題です)
3-2. 競技プログラミングをやりましょう!
競技プログラミングは、プログラミングを使って問題を解いていく競技です!もちろん、上に挙げた「Project Euler」も競技プログラミングの一例です。
みなさんお分かりかもしれませんが、競技プログラミングではもちろん速いコーディングも重要ですが、これだけではありません!問題を解くためのアルゴリズムの考察がとても重要になっています。
Project Euler 以外にもおすすめの競技プログラミングのサイトはたくさんあります。すべて世界的なウェブサイトとなっており、世界中のプロなプログラマーたちと直接対決することができます!
- AtCoder:高橋直大さん (@chokudai) らが運営している、日本発だが世界的な競技プログラミングのサイト。日本中で有名で、新聞記事として載ることも。日本で運営されているので、コンテストでは日本語の問題文も提供されている。
- TopCoder:競技プログラミングの黎明期 2001 年に始まって今もなお続いている、アメリカ発の世界的な競技プログラミングのサイト。問題文は英語だが、面白いと思うのでかなりおすすめ。
- CodeForces:ロシア発の競技プログラミングのサイト。多くのコンテストが開かれている。
今挙げた 3 つの競技プログラミングのサイトには、参加者に「レーティング」というものがついていて、コンテストの結果によって上下します。また、レーティングによって色 (例えば TopCoder だと灰<緑<青<黄<赤) がついており、赤色がついた人は「レッドコーダー」とよばれ、実力者の象徴となっています。
競技プログラミングはとても楽しいです!まだ始めていない人は、ぜひやってみましょう!
以下、競技プログラミングに関しての参考資料です。
- 数学得意じゃない系の社会人エンジニアに競プロとAtCoderを全力で布教したい。あるいは競プロのよくある誤解と楽しむコツ by @kirimin
- AtCoder に登録したら次にやること ~ これだけ解けば十分闘える!過去問精選 10 問 ~ by @drken
- 競技プログラミングって何? (はじめての高校生向け) by @sifue
- 競プロはいいぞ by @ysugiyama12
4. おわりに
これで記事は以上です。記事作成で色々なアドバイスをしてくださった @e869120 さん、ありがとうございました。高校生が書く記事なので読みにくいところも多かったかもしれませんが、最後まで読んでいただきありがとうございます!
-
2019 年 3 月 14 日に、Emma Haruka Iwao さんが Google 社のクラウドコンピューティングサービスを使い、31,415,926,535,897 桁の円周率が計算されました。これが現在の世界記録です。 ↩
-
「拡張ユークリッド互除法」を使うと、さらに高速に計算することができます。参考資料:拡張ユークリッドの互除法 〜 一次不定方程式 ax + by = c の解き方 〜 by @drken ↩
-
$2n$ 次の整数係数多項式 $f(x)$ が「$n$ 次の整数係数多項式の 2 乗」で表されるかどうかは、$f(x) = g(x)^2$ として $g(x)$ の $x^n$ の係数から順に求めていくと良いです。例えば $f(x) = 4x^4 - 8x^3 + 8x^2 - 4x + 1$ のとき、$g(x)$ の $x^2$ の係数は明らかに $2$ です。すると、$x^3$ の係数が $-8$ なことより $x^1$ の係数も $-2$ であることも分かる、みたいなイメージです。 ↩
-
具体例として、「ルービックキューブはどんな場合でも 20 手以内で揃えられる」ことを Tomas Rokicki さん (radeye さん) らが証明するとき、パターンをできるだけ絞り込む方法が使われています。参考資料:cube20.org ↩