時系列データの時間差を発見する:相互相関係数の活用
時系列データでは、何らかのアクションを行ってから実際にその効果が現れるまでにタイムラグが生じることがあります。この記事では、SPSS Modelerを使って相互相関係数を計算し、2つの時系列データ間にどれだけの時間差があるかを発見する方法をご紹介します。
1.想定される利用目的
・機械に設定した値が何秒後に実際の値に反映されるか
・マーケティングで発行したメールが何日後に開封されるか
・マーケティング・キャンペーンが何日後に効果がでるか
2.サンプルストリームのダウンロード
- テスト環境
- Modeler 18.6
- Windows 11
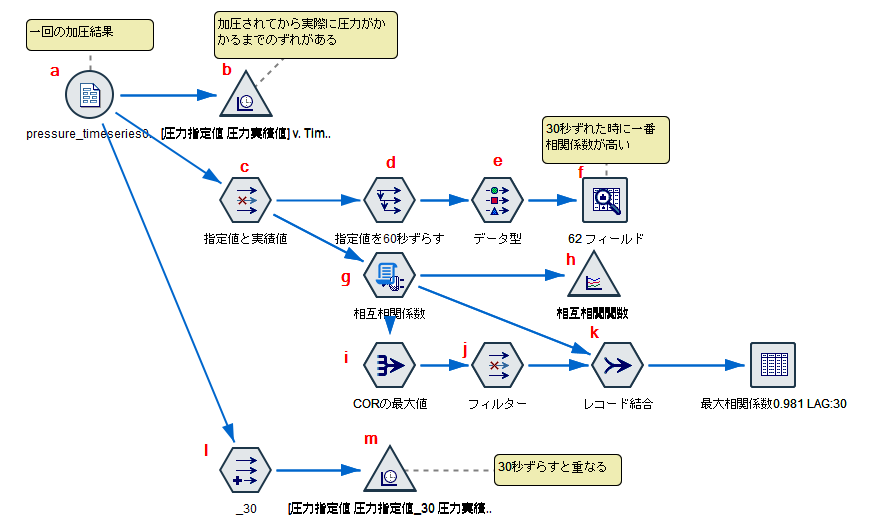
3.サンプルストリームの説明
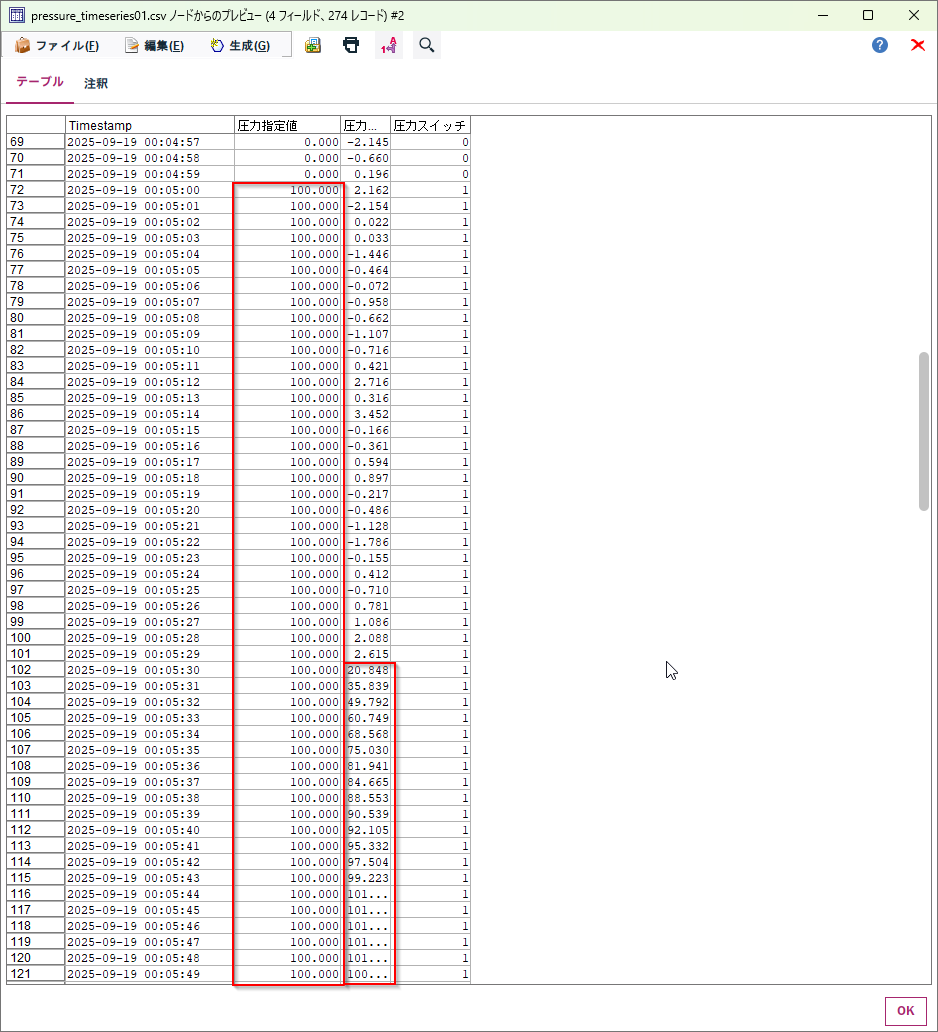
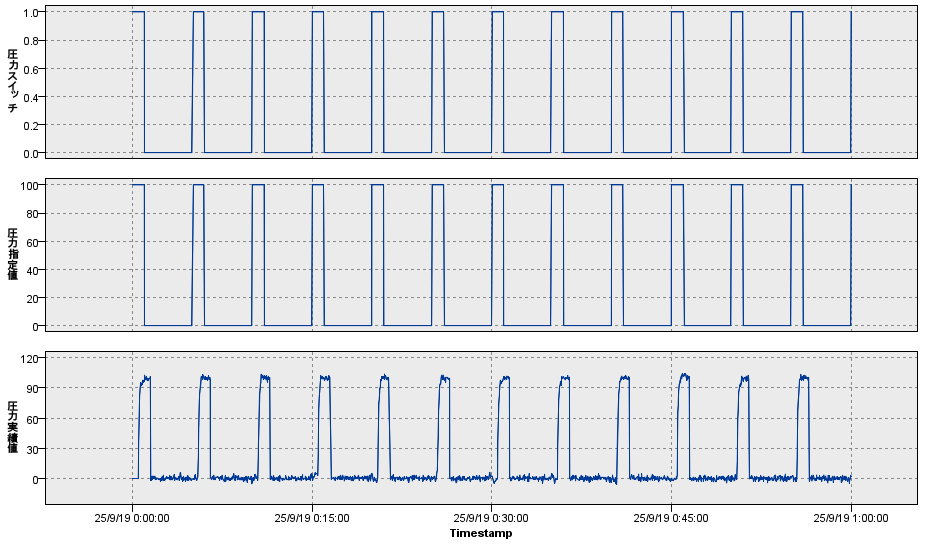
a.入力するデータは以下の通りです。
00:05:00から100の圧力が指定されて、00:05:30くらいから圧力がかかっています。この30秒の差があることを求めていきます。
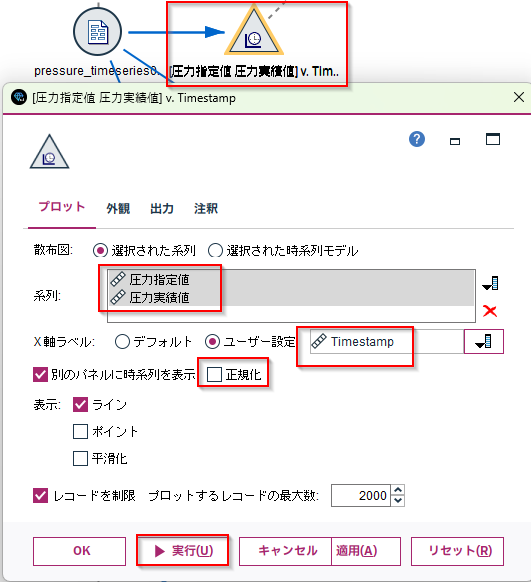
b.[時系列グラフ]ノードでグフフを書きます。
系列に 「圧力指定値」と「 圧力実績値」をセットします X 軸には「タイムスタンプ」を設定します。 「正規化」のチェックボックスを外し、 実行します。
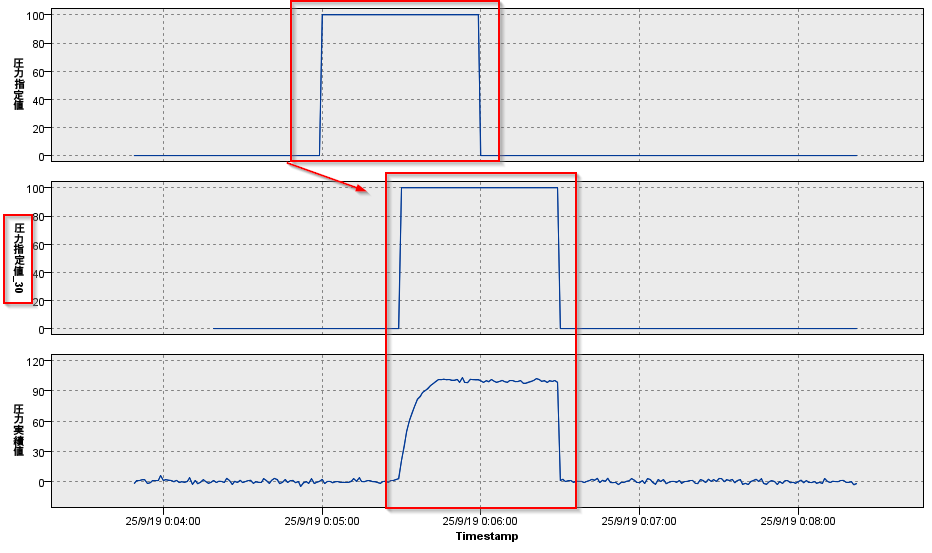
以下のように圧力を指定してから実際に圧力かかるまで30秒ぐらいかかっていることがわかります。
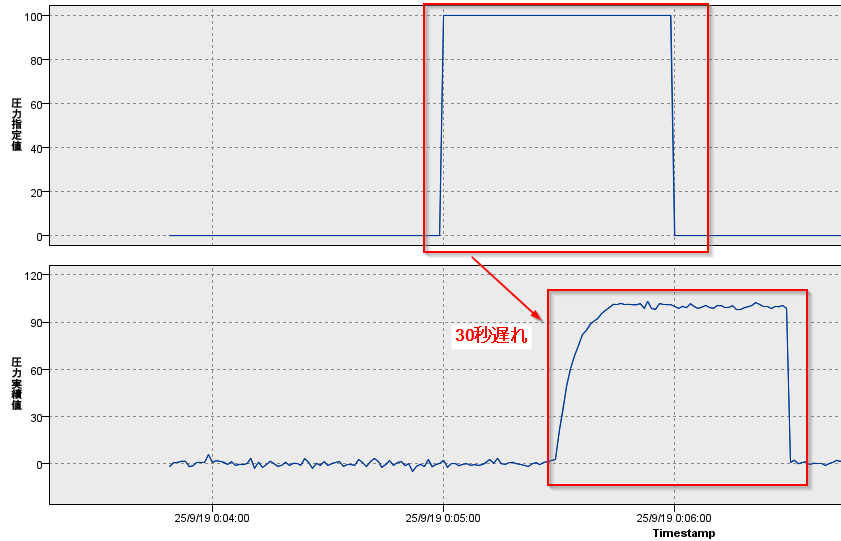
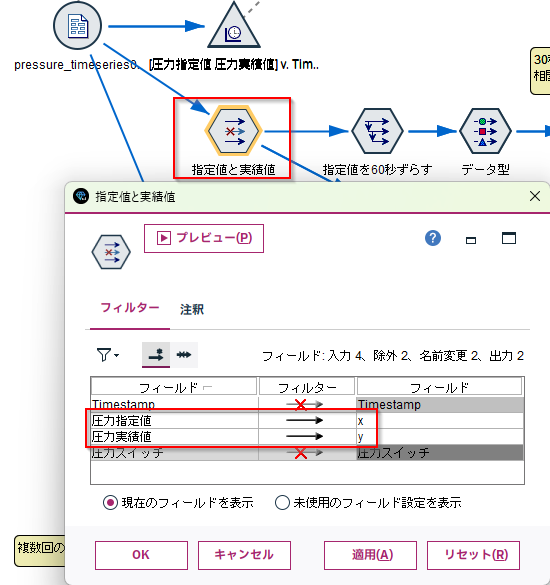
c.[フィルター]ノードを編集します。「圧力指定値」と「 圧力実績値」をそれぞれ「x」と「y」に変更しています。これはどんなデータにでも使えるように汎用的な変数名にしています。このxとyに対して相互相関係数を計算します。
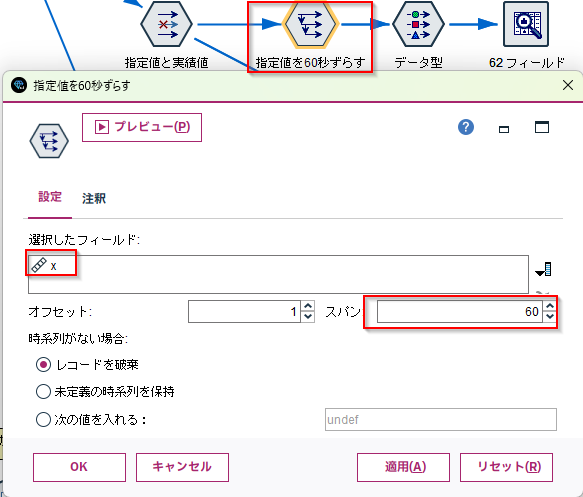
d.[時系列]ノードで60秒 分 データをずらします。
xのフィールドに選びます。 そしてスパンを60にします。
この時点で以下のようなデータになります。xの値が1秒ごとに ずれたデータが60個できています。
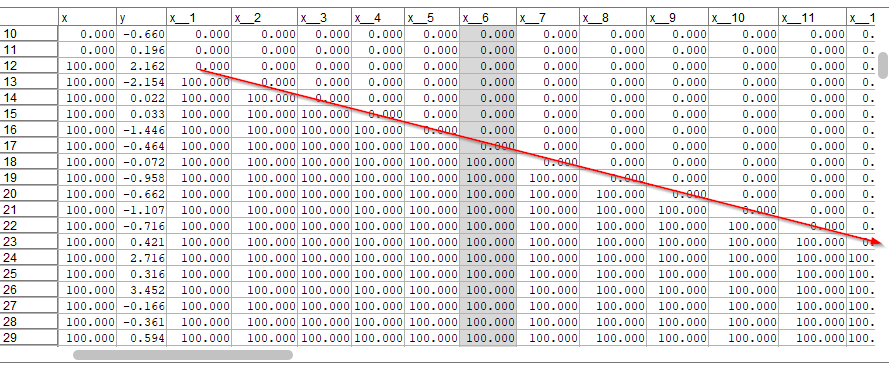
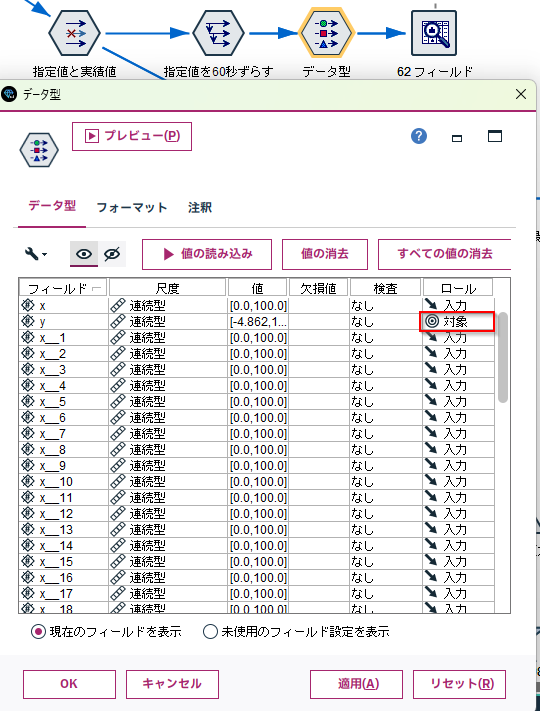
e.[データ型]ノードで yのロールを「対象」にします。
f.[データ検査]ノードを実行します。
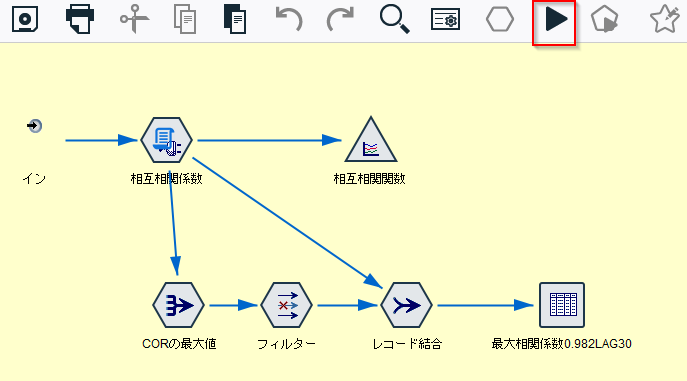
「相関」係数で並べ替えます。一番相関係数が高いのは「x_30」でした。つまりx「圧力指定値」とを30秒ずらした時にy「 圧力実績値」と最も相関があるということになります。

Pythonで相互相関係数を計算する
上の[時系列]ノードと[データ検査]ノードをつかった方法では、60秒ずらした中での相互相関係数を求めましたが、データ全体での相互相関係数を求めたい場合、相互相関係数を可視化したい場合には[拡張の変換]ノードをつかってPythonで算出するのが便利です。
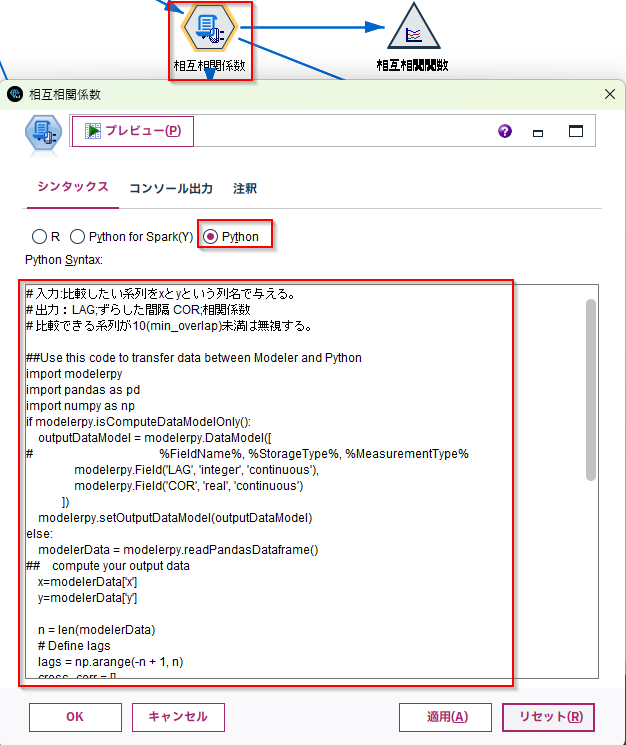
g.[拡張の変換]ノードを編集します。
言語を Python にして以下のプログラムをペーストします。
最初と最後の10件を切り取ってデータを全て ずらし 相関係数を取っています。比較したい系列をxとyという列名で与えます。結果としては LAG(ずらした間隔) COR(相関係数)の2列が返ります。
# 入力:比較したい系列をxとyという列名で与える。
# 出力:LAG;ずらした間隔 COR;相関係数
# 比較できる系列が10(min_overlap)未満は無視する。
##Use this code to transfer data between Modeler and Python
import modelerpy
import pandas as pd
import numpy as np
if modelerpy.isComputeDataModelOnly():
outputDataModel = modelerpy.DataModel([
# %FieldName%, %StorageType%, %MeasurementType%
modelerpy.Field('LAG', 'integer', 'continuous'),
modelerpy.Field('COR', 'real', 'continuous')
])
modelerpy.setOutputDataModel(outputDataModel)
else:
modelerData = modelerpy.readPandasDataframe()
## compute your output data
x=modelerData['x']
y=modelerData['y']
n = len(modelerData)
# Define lags
lags = np.arange(-n + 1, n)
cross_corr = []
# Compute cross-correlation using np.corrcoef, excluding lags with low overlap
min_overlap = 10
for lag in lags:
if lag < 0:
x_seg = x[-lag:]
y_seg = y[:n + lag]
else:
x_seg = x[:n - lag]
y_seg = y[lag:]
if len(x_seg) >= min_overlap:
corr = np.corrcoef(x_seg, y_seg)[0, 1]
else:
corr = np.nan
cross_corr.append(corr)
#print(cross_corr)
df = pd.DataFrame({'LAG': lags,'COR': cross_corr})
outputData = df
modelerpy.writePandasDataframe(outputData)
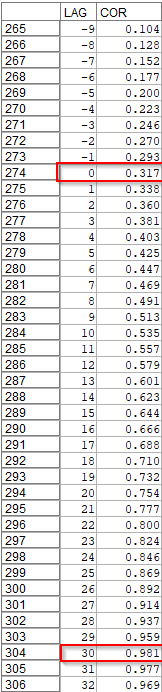
以下のような結果が返ります。
LAGがマイナスー273から0をはさんで273まであり、ここでは30秒ずらしたところが0.981で最も高い相互相関係数になっています。
h.[線グラフ]ノードで相互相関係数を可視化します。
x フィールドにラLAGyフィールドにCORをセットして、 実行します。
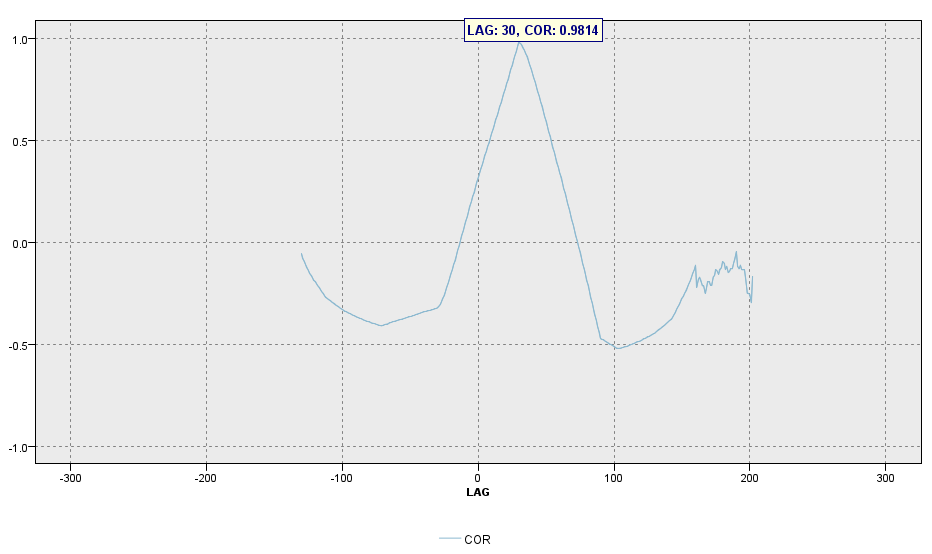
やはりピークは30秒だということがグラフからもわかります。
なお、山が複数できるような場合などは何か周期があるかもしれません。
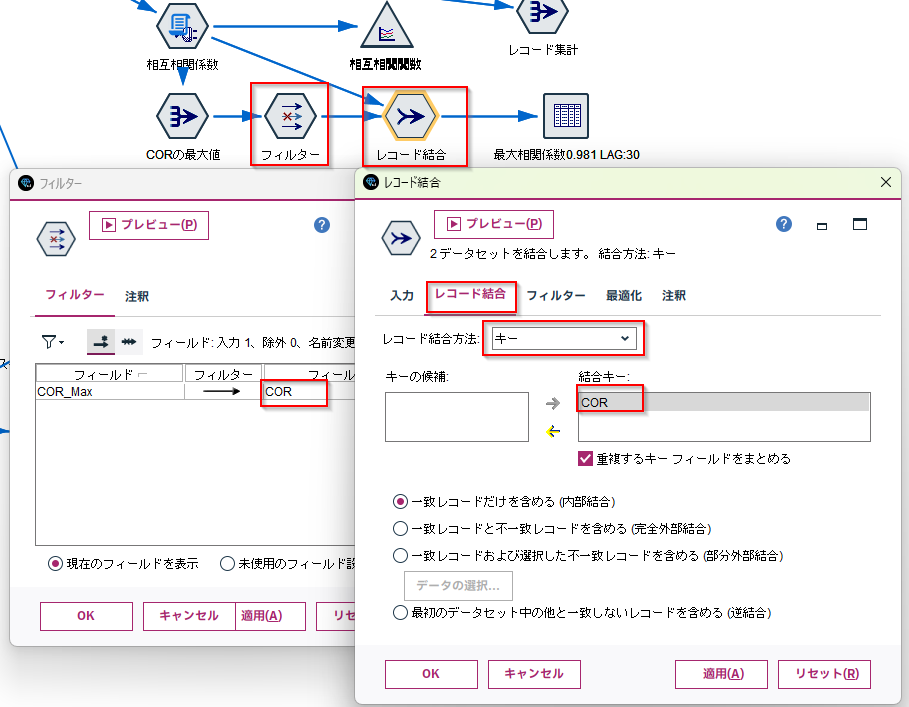
i.[集計]ノードを編集します。
集計フィールドにCORを選び 最大にチェックをつけます。レコード度数のチェックは外しておきます。

jk.[フィルター]ノードでCOR_MaxをCORに変更し レコード結合モードでCORをキーに結合します。これで最大の相関係数のLAGが抽出できます。
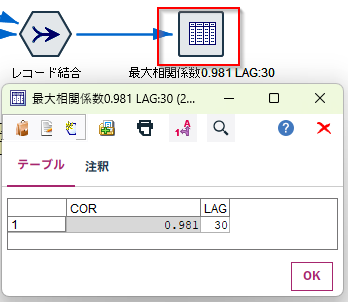
[テーブル]を実行します。
30秒ずらしたところが0.981で最も高い相互相関係数です。
30秒のずれの妥当性を可視化して確認する
30秒のずれという結果が妥当かどうかを可視化して確認してみます。
l.[フィールド作成]ノードで30秒ずらした「圧力指定値」を@OFFSET(@FIELD,30)作ります。
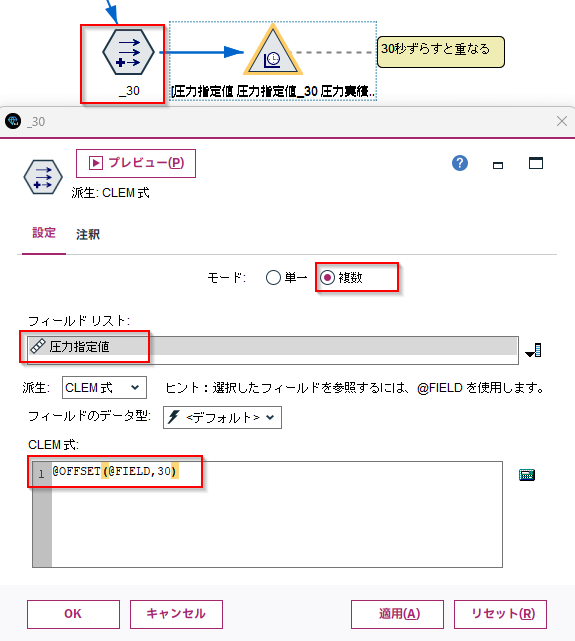
m. [時系列グラフ]ノードでグフフを書きます。
系列に 「圧力指定値」、「圧力指定値_30」と「圧力実績値」をセットします X 軸には「タイムスタンプ」を設定します。 「正規化」のチェックボックスを外し、 実行します。
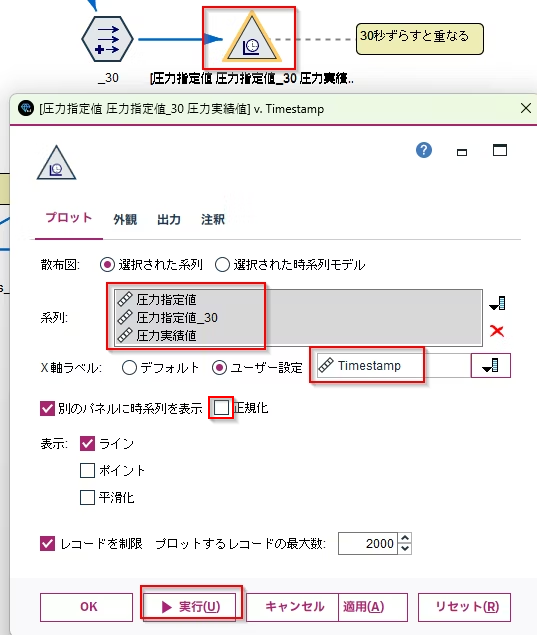
確かに「圧力指定値」の30秒後のデータと「圧力実績値」がほぼ重なることがわかります。
複数回サイクルの相互相関係数を算出
今までは、1回サイクルの相互相関係数をもとめて、その時間差を求めてきました。
次に以下のように複数回加圧した場合の時間差の平均を求めてみます。
[フィールド作成]ノードでサイクルのインデックスCIDEXとサイクル内の圧力をかけてからの時間のインデックスPIDXを作ります。

[集計]ノードでPIDXをキーフィールドに設定し 「圧力指定値」と「圧力実績値」の平均を出します 。
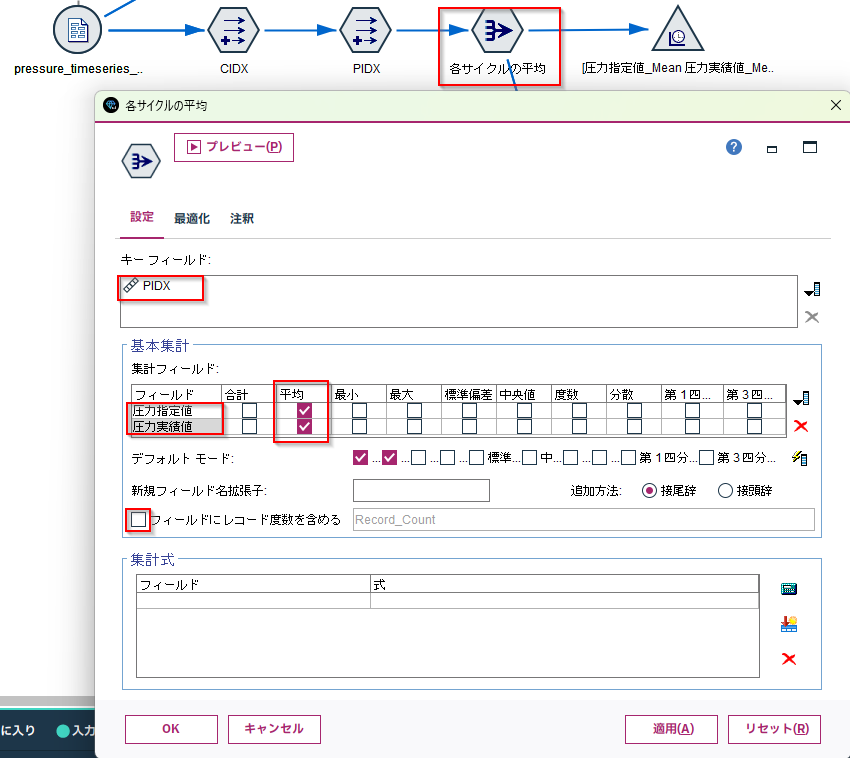
[時系列グラフ]ノードでグフフを書きます。全サイクルの平均の「圧力指定値」と「圧力実績値」が可視化されました。
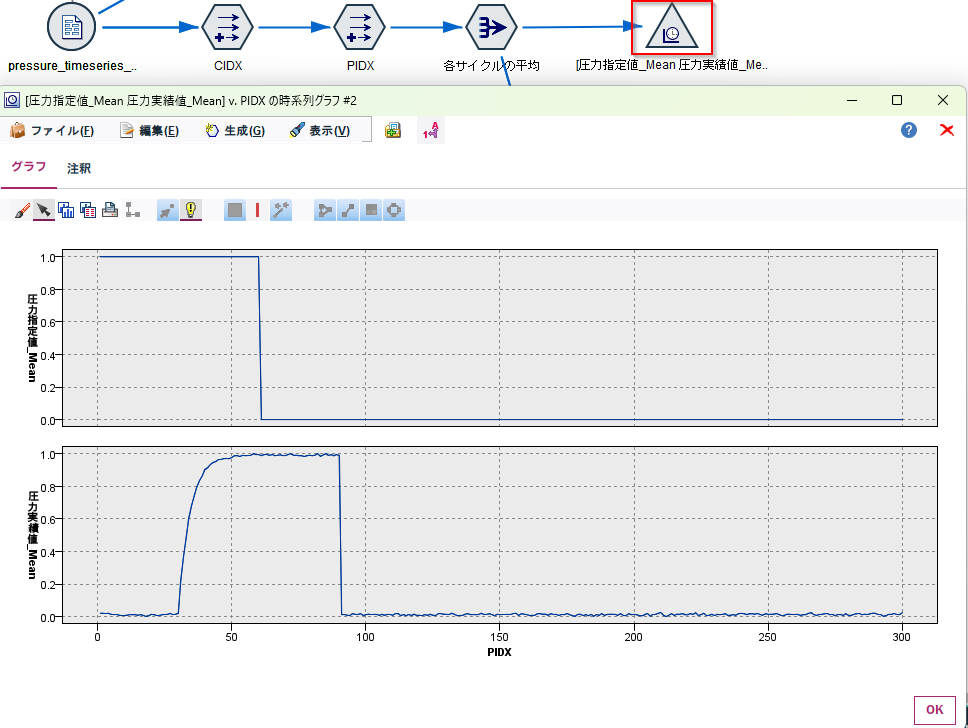
[フィルター]ノードで「圧力指定値_Mean」と「圧力実績値_Mean」をそれぞれ「x」と「y」に変更し、「PIDX」はフィルタリングしています。
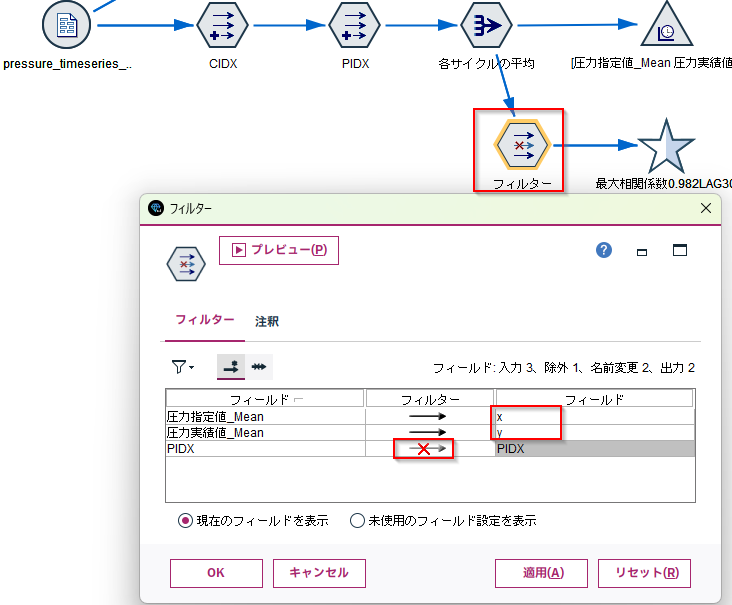
スーパーノードの中には上記のgノード以降が入っています。これを実行します。
やはり、30秒ずらしたところが最大の相互相関係数です。0.982でした。

4.参考情報
SPSS Modeler ノードリファレンス目次
SPSS Modeler 逆引きストリーム集(データ加工)