きちんと理解する Graph Convolution Networks (2)

目次

前の記事で扱った内容
1.グラフ深層学習とは
2.グラフ深層学習ができること
3.グラフフーリエ変換を理解する

この記事で扱う内容
4.グラフ信号のフィルタリング
5.GCN
6.終わりに

4. グラフ信号のフィルタリング

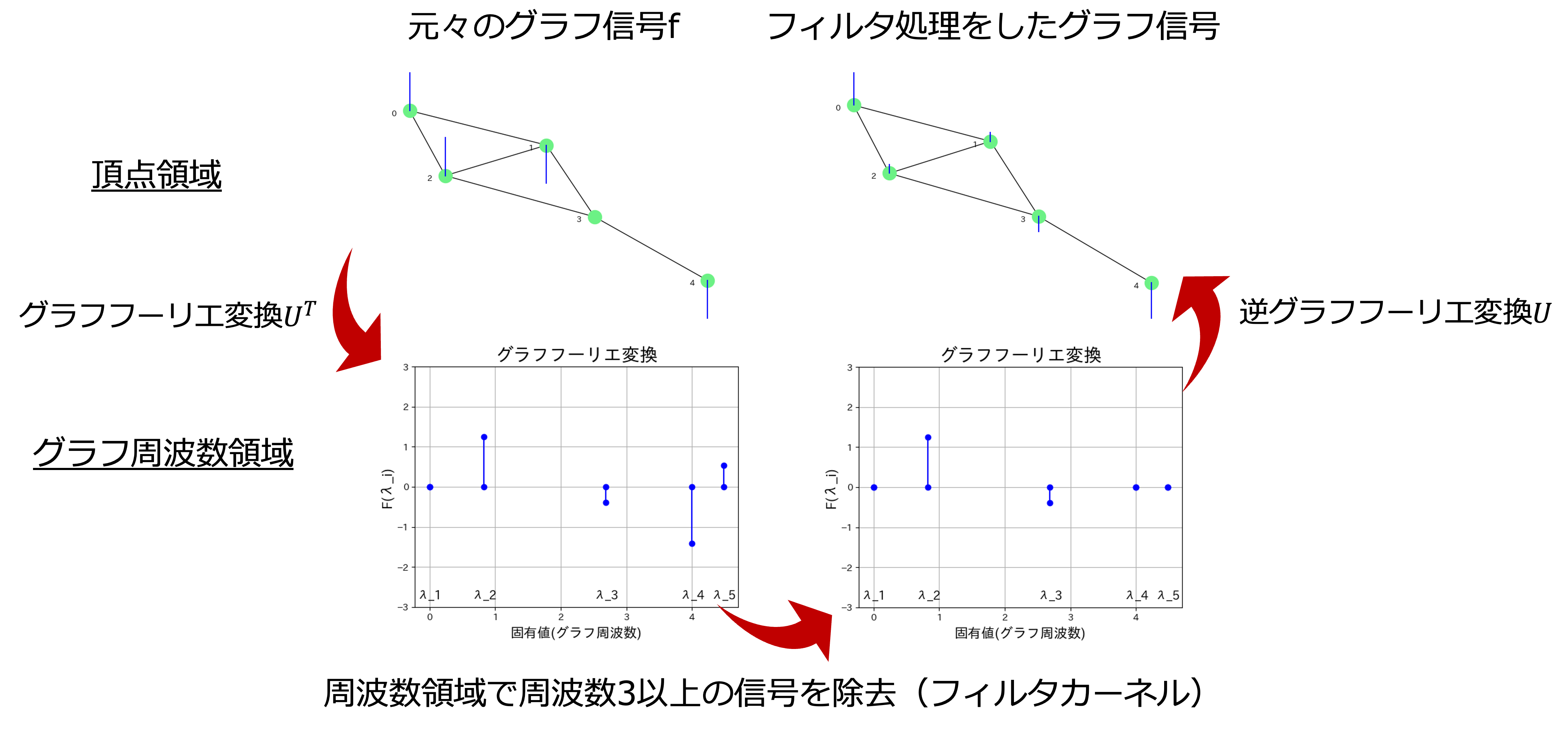
グラフフーリエ変換によって，グラフ信号を周波数領域に変換することができました．
では，3.1.2のように周波数領域でフィルタリングを試してみましょう．

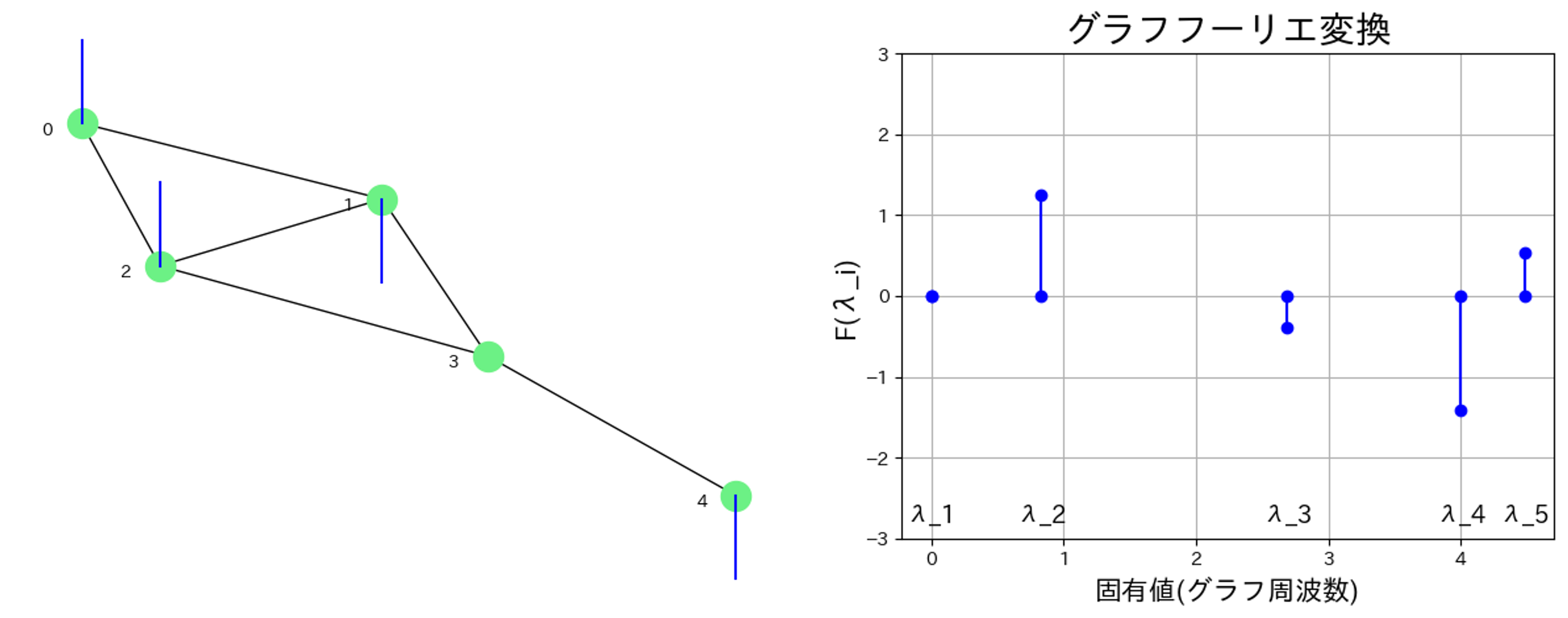
4.1 フィルタリングの例

前の記事の例1の図をもう一度載せます．

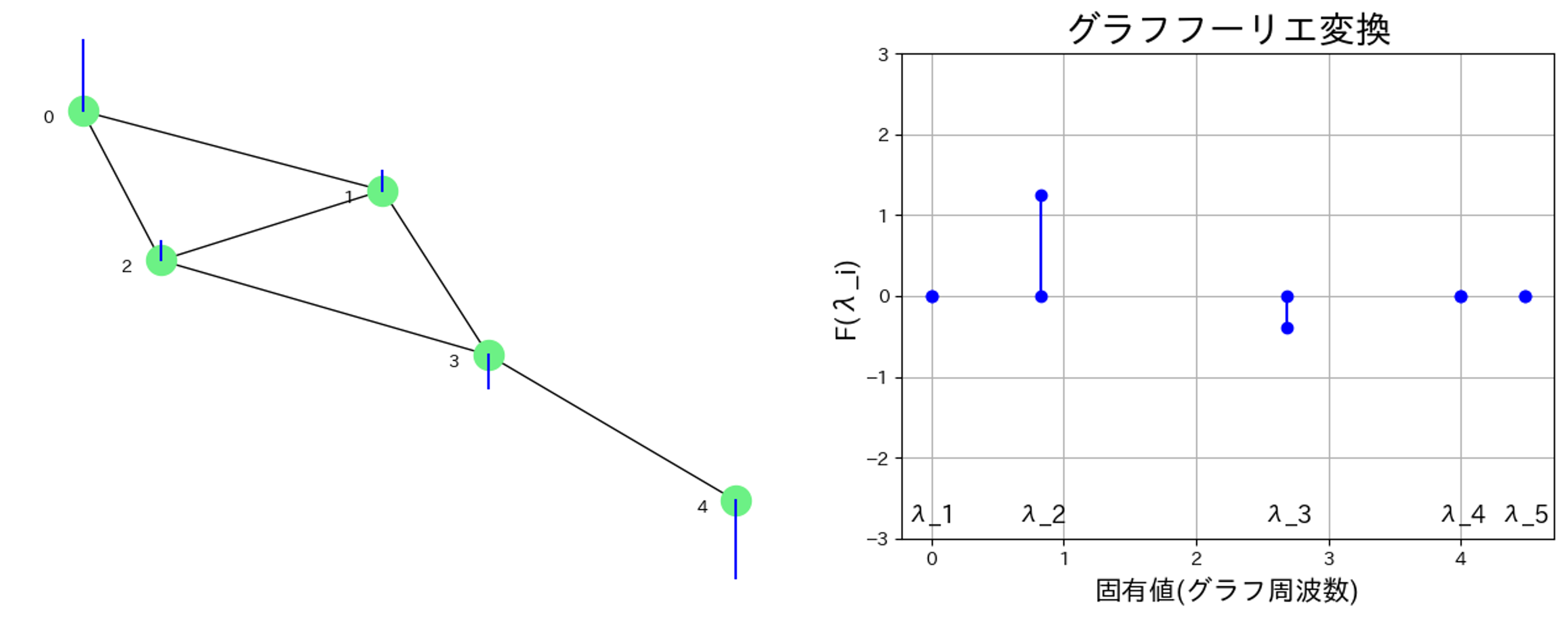
このグラフ信号にローパスフィルタを適用してみましょう．
グラフ周波数が3より大きいところの成分を0，，つまり$F(\lambda_4)=F(\lambda_5)=0$とします．
その後，逆グラフフーリエ変換によってグラフ信号を再構成します．
$$
f(k) = \sum_{i=0}^{N-1} {F}(\lambda_i) \cdot u_{\lambda_i}(k)
$$

高周波成分を取り除いたことで，フィルタを適用する前に比べ，グラフが滑らかになったのがわかりますね．

4.2 グラフフーリエ変換の行列表記

今後のために，グラフフーリエ変換を行列で表記します．
グラフラプラシアン$L$の固有値分解
$$
L = U\Lambda U^T
$$
ただし，
$$
U = [u_1,u_2,...,u_N]， \Lambda=diag([\lambda_1,\lambda_2,...,\lambda_N])
$$
です

グラフフーリエ変換

$$
{F}(\lambda_i) = \sum_{k=0}^{N-1} f(k) \cdot u_{\lambda_i} (k)
$$
は行列で書くと，
$$
F = U^Tf
$$

メモ：$u_{\lambda_i}$は$U$の列ベクトルなので，行列でまとめて計算する際は$U^Tf$となリます．

逆グラフフーリエ変換

$$
f(k) = \sum_{i=0}^{N-1} {F}(\lambda_i) \cdot u_{\lambda_i}(k)
$$
は行列で書くと，
$$
f = UF
$$
となります．

次に，フィルタリングの操作を行列で表すことを考えます．1,2,3のステップに分けて説明します．

1.グラフ信号を周波数領域に変換
$$
F = U^Tf
$$
2.周波数領域でフィルタリングなどの処理を行う．
　フィルタカーネルと呼ばれる以下の行列をFに左から掛けることでフィルタリングを行う．
　各周波数の成分に対して処理をするだけです．

\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1) & 0 & \ldots & 0 \\\
0 & H(\lambda_2) & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & H(\lambda_N)
\end{array}
\right)
\end{eqnarray}

F_{filtered} = 
\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1) & 0 & \ldots & 0 \\\
0 & H(\lambda_2) & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & H(\lambda_N)
\end{array}
\right)
\end{eqnarray}
F

　先ほどの3.3.3のローパスフィルタでは，$F(\lambda_4)=F(\lambda_5)=0$としましたが，これをフィルタカーネルで表現すると，以下のようになります．

\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1)=1 & 0 & 0 & 0  & 0\\\
0 & H(\lambda_2)=1 & 0 & 0  & 0\\\
0 & 0 & H(\lambda_3)=1 & 0  & 0\\\
0  & 0 & 0 & H(\lambda_4)=0  & 0\\\
0  & 0 & 0 & 0 & H(\lambda_5)=0
\end{array}
\right)
\end{eqnarray}

3.逆グラフフーリエ変換で再構成を行う
$$
f_{filtered} = UF_{filtered}
$$

以上の1,2,3をまとめると，以下のように書くことができます．

f_{filtered} = U 
\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1) & 0 & \ldots & 0 \\\
0 & H(\lambda_2) & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & H(\lambda_N)
\end{array}
\right)
\end{eqnarray}
U^Tf

フィルタリングの流れを図にすると以下のようになります．

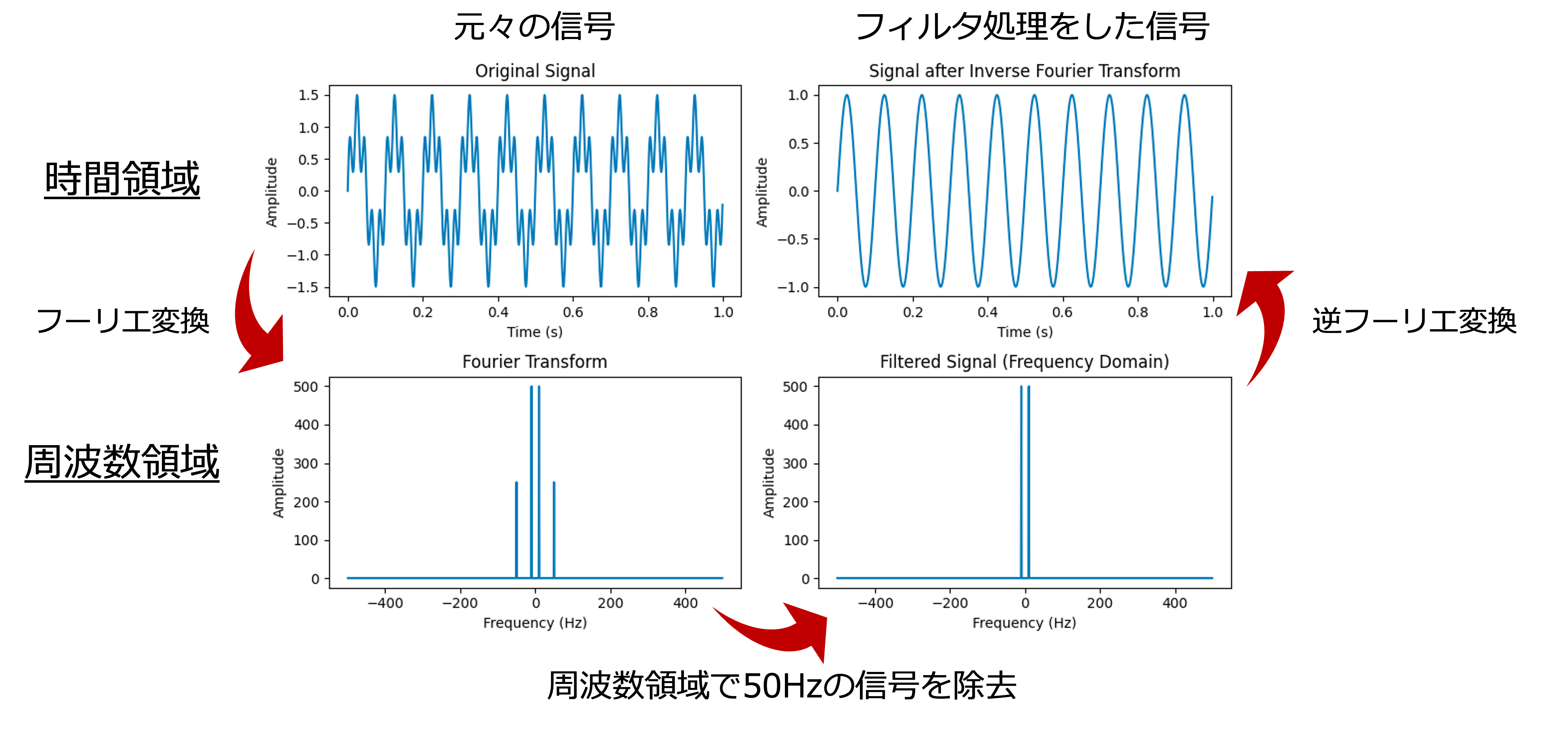
フーリエ変換の時とやってることは同じです.3.1.2の図を再掲します．

4.3 深層学習によるフィルタカーネルの最適化

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
後ほど詳しく紹介しますが，この論文を参考にしました，

4.3.1 フィルタカーネルのパラメータ化

グラフ信号のフィルタリングについてもう少し考えてみます．

f_{filtered} = U 
\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1) & 0 & \ldots & 0 \\\
0 & H(\lambda_2) & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & H(\lambda_N)
\end{array}
\right)
\end{eqnarray}
U^Tf

フィルタカーネル$diag([H(\lambda_1),H(\lambda_2)...,H(\lambda_n)])$を良い感じに設計すれば良い感じの$f_{filtered}$が得られそうです．

例えば，低周波成分が重要だ！となればローパスフィルタをかければ良いですし，逆に高周波成分が重要だ！となればハイパスフィルタを掛ければ良いです．

例えば，$H(\lambda_i)=\frac{1}{\lambda_i+1}$，つまり

\begin{eqnarray}
\left(
\begin{array}{cccc}
H(\lambda_1)=\frac{1}{\lambda_1+1} & 0 & \ldots & 0 \\\
0 & H(\lambda_2)=\frac{1}{\lambda_2+1} & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & H(\lambda_N)=\frac{1}{\lambda_N+1}
\end{array}
\right)
\end{eqnarray}

などとすることもできます．この場合は，$\lambda_i$が大きいほど$H(\lambda_i)$が小さくなるのでローパスフィルタになります．

試行錯誤して良い感じのフィルタカーネルを見つける必要があります．でもそれは大変そうですね...

しかし，深層学習を用いれば人手で設計せずとも，最適なフィルタカーネルを見つけられます！

フィルタカーネルを以下のようにパラメータとして最適化すれば良いのです．
例えば，分類タスクならクロスエントロピーロスを使用して，ロスを逆伝搬させれば良いでしょう．
（誤差逆伝搬法やロス関数の設計はここでは深く説明しません．）

f_{filtered} = U 
\begin{eqnarray}
\left(
\begin{array}{cccc}
\theta_1 & 0 & \ldots & 0 \\\
0 & \theta_2 & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & \theta_N
\end{array}
\right)
\end{eqnarray}
U^Tf

簡略化して，今後は以下のように記述します．

f_{filtered} = Ug_θ(Λ)U^Tf

今の場合は，$g_θ(Λ)=diag([\theta_1,\theta_2...,\theta_N])$と書けます．

ここで問題点があります．
グラフフーリエ変換では，グラフ全体の情報を使用するので，ノード$i$からみた時，ノード$j$が隣にあっても遠いところにあっても一緒です．
つまり，近くにどのような信号があるかは見ていないのです．

ということで，近傍の情報を活用するようにフィルタカーネル$g_θ(Λ)$を設計しましょう．

4.3.2 多項式フィルタカーネル

フィルタカーネルを以下のように設計します．
$$
g_θ(\Lambda) = \sum_{k=0}^{K-1}\theta_k\Lambda^{k}
$$

K=3の場合，
$$
g_θ(\Lambda) = \theta_0\Lambda^{0} + \theta_1\Lambda^{1} + \theta_2\Lambda^{2}
$$
$\Lambda=diag([\lambda_1,\lambda_2,...,\lambda_n])$なので，

g_θ(\Lambda) = \theta_0
\begin{eqnarray}
\left(
\begin{array}{cccc}
\lambda_1^0 & 0 & \ldots & 0 \\\
0 & \lambda_2^0 & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & \lambda_N^0\\\
\end{array}
\right)

+

\theta_1\left(
\begin{array}{cccc}
\lambda_1^1 & 0 & \ldots & 0 \\\
0 & \lambda_2^1 & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & \lambda_N^1\\\
\end{array}
\right)

+

\theta_2\left(
\begin{array}{cccc}
\lambda_1^2 & 0 & \ldots & 0 \\\
0 & \lambda_2^2 & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & \lambda_N^2\\\
\end{array}
\right)

\end{eqnarray}

全て足すと，

g_θ(\Lambda) =
\begin{eqnarray}
\left(
\begin{array}{cccc}
\theta_0\lambda_1^0  + \theta_1\lambda_1^1 + \theta_2\lambda_1^2 & 0 & \ldots & 0 \\\
0 & \theta_0\lambda_2^0  + \theta_1\lambda_2^1 + \theta_2\lambda_2^2  & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & ... & \theta_0\lambda_N^0  + \theta_1\lambda_N^1 + \theta_2\lambda_N^2 \\\
\end{array}
\right)
\end{eqnarray}

・$\Lambda^0$が0次近傍，つまり自分自身
・$\Lambda^1$が1次近傍，つまり1hop先のノード
・$\Lambda^2$が1次近傍，つまり2hop先のノード
一般に，$\Lambda^k$がk次近傍のノードから情報を集約することに繋がるそうです．
（この理由がわかっていません．詳しくは Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering の(3)式を見てください...）

$$
g_θ(\Lambda) = \theta_0\Lambda^{0} + \theta_1\Lambda^{1} + \theta_2\Lambda^{2}
$$
において，
・$\theta_0$は0次近傍（＝自分自身）の情報をどのくらい使うか
・$\theta_1$は1次近傍の情報をどのくらい使うか
・$\theta_2$は2次近傍の情報をどのくらい使うか
一般に，$\theta_k$はk次近傍の情報をどのくらい使うかを表します．

例えば，フィルタカーネルの最適化の結果が，
$$
\theta_0=0.3, \theta_0=0.5, \theta_0=0.1,
$$
となれば，重要度は 1次近傍＞0次近傍＞2次近傍 ということになります．

ただ，この多項式フィルタカーネルにも問題があります．
その問題が計算量です．

まずグラフラプラシアン$L$の固有値分解に$O(N^3)$の計算が必要です．
そして，フィルタリングの行列演算は$O(N^2)$の計算量であるため，大きなデータではものすごく時間がかかってしまいます．
固有値分解は1回だけで良いですが，フィルタリングはエポックごとに毎回行う必要があります．
ノード数が100くらいなら大丈夫ですが，数万，数十万ともなるとまともに動かないでしょう．

4.3.3 ChebNet（チェビシェフの多項式による多項式フィルタカーネルの近似）

多項式フィルタカーネルにおけるフィルタリングの計算量を$O(K|\mathcal{E}|)$に減らす手法があります．
$K$は近傍の$K$で，$|\mathcal{E}|$はエッジの本数です．多くのグラフでは，$N^2 > K|E|$であるため計算量の削減に繋がります．

その手法を提案している論文が先ほども紹介した， Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering です．（ChebNetとして知られており，Pytorch GeometricではChebConvとして実装されています．）

この手法では，以下のチェビシェフの多項式を利用します．

\mathcal{T}_k(x) = 2x\mathcal{T}_{k-1}(x)-\mathcal{T}_{k-2}\\\
, \mathcal{T}_0(x)=1\\\
, \mathcal{T}_1(x)=x\\\

チェビシェフの多項式は漸化形であるところがポイントです．

以下がChebNetの式です．
$$
g_θ(\Lambda) = \sum_{k=0}^{K}\theta_k \mathcal{T_k(\tilde{\Lambda)}}\
$$
$$
\tilde{\Lambda} = \frac{2}{\lambda_{max}}{\Lambda} - I
$$

まず，2つ目の式に注目します．$\lambda_{max}$は一番大きいグラフラプラシアンの固有値です．
固有値$\lambda_1,\lambda_2,...,\lambda_n$の値の範囲は，$[0,\lambda_{max}]$で， $\lambda_{max}$で割ると，$[0,1]$となります．次に2をかけると$[0,2]$に，そして1を引くと$[-1,1]$となります．
2つ目の式は再スケーリングと呼ばれ，この式を行うことで，固有値を$[-1,1]$にすることができます．
再スケーリングを行うことによって，学習の際に，値が爆発的に大きくなったり消失したりせず安定します．

多項式フィルタカーネルは以下の式でした．
$$
g_θ(\Lambda) = \sum_{k=0}^{K-1}\theta_k\Lambda^{k}
$$

ChebNetは，$\Lambda^{k}$を$\mathcal{T_k(\tilde{\Lambda)}}$に置き換えていることがわかります．

$\Lambda^{k}$と$\mathcal{T_k(\tilde{\Lambda)}}$の対応としては，
$\Lambda^{0}=I$，　$\mathcal{T_0(\Lambda)}=I$，
$\Lambda^{1}=\Lambda$，　$\mathcal{T_1(\Lambda)}=\tilde{\Lambda}$，
$\Lambda^{2}$，　$\mathcal{T_2(\Lambda)}=\tilde{\Lambda}^2-I$，
$\Lambda^{3}$，　$\mathcal{T_3(\Lambda)}=4\tilde{\Lambda}^3-3\tilde{\Lambda}$，
$\Lambda^{4}$，　$\mathcal{T_4(\Lambda)}=8\tilde{\Lambda}^4-8\tilde{\Lambda}^2+I$,
$...$

のように対応しています．そこそこ似てますね．

計算量の話をするために，ChebNetの式変形します．
フィルタリング全体の式で考えます．

行列表記したフィルタリングの式
$$
f_{filtered} = Ug_θ(Λ)U^Tf
$$

ChebNetの式
$$
g_θ(\Lambda) = \sum_{k=0}^{K}\theta_k \mathcal{T_k(\tilde{\Lambda)}}
$$

$$
\tilde{\Lambda} = \frac{2}{\lambda_{max}}{\Lambda} - I
$$

これらをまとめると，

f_{filtered} = U  \Biggl(\sum_{k=0}^{K}\theta_k \mathcal{T_k(\tilde{\Lambda)}}\Biggr)  U^T
= \sum_{k=0}^{K}\theta_k* U\mathcal{T_k(\tilde{\Lambda)}} U^T *f

$\tilde{L} = \frac{2L}{λ_{max}} − I$ を用いると，

f_{filtered} =\sum_{k=0}^{K}\theta_k \mathcal{T_k}(\tilde{L})f

ここの式変形は，上の論文に詳しく載っていませんが，$L=U\Lambda U^T$　から $\tilde{L}=U\tilde{\Lambda} U^T$， 及び， $\mathcal{T_k}(\tilde{L}) = U\mathcal{T_k(\tilde{\Lambda})} U^T$ がわかります．（証明略）

まとめると，ChebNetの計算の流れは以下の1,2,3になります．

1.$L$を固有値分解して，$\lambda_{max}$を求める．

2.$\tilde{L} = \frac{2L}{λ_{max}} − I$を計算する．

3.$f_{filtered} =\sum_{k=0}^{K}\theta_k \mathcal{T_k}(\tilde{L})f$でフィルタリングを行う．

では，なぜチェビシェフの多項式で近似することで計算量を削減できるかを考えます．
3の式を$\Sigma$を使わずに書きます．
$$
f_{filtered} =\sum_{k=0}^{K}\theta_k \mathcal{T_k}(\tilde{L})f = \theta_0 \mathcal{T_0}(\tilde{L})f + \theta_1\mathcal{T_1}(\tilde{L})f + \theta_2 \mathcal{T_2}(\tilde{L})f + ... + \theta_{K-1} \mathcal{T_{K-1}}(\tilde{L})f
$$

チェビシェフの多項式の定義式の$x$に，$\tilde{L}$を代入すると，以下のようになります．

\mathcal{T}_k(\tilde{L}) = 2\tilde{L}\mathcal{T}_{k-1}(\tilde{L})-\mathcal{T}_{k-2},\ \mathcal{T}_0(\tilde{L})=I\\\
, \mathcal{T}_1(\tilde{L})=\tilde{L}\\\

この関係を使用すると，計算結果を再利用することができます． これによって，行列計算が$O(K|\mathcal{E}|)$になります．
注意：sparse matrixを使用すると，行列の積が$O(|\mathcal{E}|)$なります．

簡単に擬似コードを書いてみました ．tilde_Lが$\tilde{L}$を表します．

# 擬似コード
def ChebNet(K, tilde_L, θ, f):

    # 初期化
    f_filetered = 0
    
    # T_k_2はT_k-2を， T_k_1はT_k-1を表す．
    T_k_2 = θ[0] * I @ f # 単位行列， T_0
    T_k_1 = θ[1] * tilde_L @ f # T_1

    # k = 2,3,...K-1
    for k in range(2,K):
        T_k = 2 * tilde_L @ T_k_1 - T_k_2 # 漸化式
        f_filterd += θ[k] * T_k @ f
    
        # 更新
        T_k_2 = T_k_1
        T_k_1 = T_k

    return f_fileterd

よって，ChebNetによるフィルタリングの計算量は，
・グラフラプラシアン$L$の固有値分解：$O(N^3)$　ただし，この計算は1回だけ
・フィルタリングの行列計算...$O(K|\mathcal{E}|)$ エポックごとに計算する

5. GCN

ようやくGCNの数式に入っていきます．

5.1 GCNのアイデア

ChebNetの式を再掲します．

$$
\tilde{L} = \frac{2L}{λ_{max}} − I
$$

$$
f_{filtered} =\sum_{k=0}^{K}\theta_k \mathcal{T_k}(\tilde{L})f
$$

GCNでは，これらの式をとにかく簡略化していきます．

ChebNetの式において，
グラフラプラシアン$L$を正規化グラフラプラシアン$\mathcal{L}$に変更し，
$λ_{max}=2$， $K=1$とします．
$λ_{max}=2$と決めてしまうことで，$O(n^3)$の固有値分解をせずに済み，$K=1$とすることで，自分自身と隣接ノードしか見ないようにします．

$$
\tilde{\mathcal{L}} = \mathcal{L} − I = D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
$$
メモ：これは $\mathcal{L}= I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$を変形することで得られます．

\displaylines{
f_{filtered} = \sum_{k=0}^{2}\theta_k \mathcal{T_k}(\tilde{\mathcal{L}})f \\
= \theta_0 \mathcal{T_0}(\tilde{\mathcal{L}})f + \theta_1 \mathcal{T_1}(\tilde{\mathcal{L}})f  \\
= \theta_0 I f + \theta_1 \tilde{L}f \\
= (\theta_0I + \theta_1 \tilde{\mathcal{L}})f \\
= (\theta_0I - \theta_1 D^{-\frac{1}{2}}AD^{-\frac{1}{2}})f
}

さらに，
$\theta = \theta_0 = -\theta_1 $とします．もっと簡略化します．
そうすると，
$$
f_{filtered} = \theta(I + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})f
$$
となります．

しかし， $I + D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$ はこのままでは固有値が$[0,2]$で数値的に不安定で，勾配が爆発したり消失する恐れがあるので，以下のトリックを使用します．

\displaylines{
I + D^{-\frac{1}{2}}AD^{-\frac{1}{2}} → \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} \\
\tilde{A} = A + I, \tilde{D}は\tilde{A}の次数行列
}

以上より，

$$
f_{filtered} = \theta \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} f
$$

となります．

5.2 グラフ信号の一般化

グラフ信号からスタートしたので，これまで$f$ 及び， $f_{filtered}$という表記を使用していました．
グラフ信号は各ノードが値（スカラー）を持っており，フィルタリングを行うことで，新たな値（スカラー）が得られました．

もっと一般の状況を考えましょう．グラフの各ノードがC次元の特徴量を持っているとします．
ここからは，$f$ではなく，$X$を使用します．

先ほどの式を書き換えると以下のようになります．

$X_i, X'_i$は共に$N$次元の列ベクトルです．
$$
X'_i = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X_i
$$

この式によって，特徴量を$X_i$から$X'_i$へ更新できます．

更新して得られた，以下のC次元の特徴量から，新たなF次元の特徴量を作成することを考えます．

(X'_0, X'_1, ...  X'_{C-1})

具体例で考えます．

下の図では，各ノードが赤，緑，青の3次元の特徴量を持ちます．
ノードごとに特徴をまとめたベクトル$X_{red},X_{green}, X_{blue}$を用意します．
ノード数が5なので，各ベクトルは5次元の列ベクトルになります．

こんな感じです．
$$
X = (X_{red},X_{green},X_{blue})
$$

\begin{eqnarray}
X_{red}=
\left(
\begin{array}{cccc}
X_{0,red} \\\
X_{1,red}  \\\
X_{2,red}  \\\
X_{3,red}  \\\
X_{4,red}  \\\
\end{array}
\right)
,
X_{green}=
\left(
\begin{array}{cccc}
X_{0,green} \\\
X_{1,green}  \\\
X_{2,green}  \\\
X_{3,green}  \\\
X_{4,green}  \\\
\end{array}
\right)
,
X_{blue}=
\left(
\begin{array}{cccc}
X_{0,blue} \\\
X_{1,blue}  \\\
X_{2,blue}  \\\
X_{3,blue}  \\\
X_{4,blue}  \\\
\end{array}
\right)

\end{eqnarray}

この特徴量を更新します．
$ X_{red}' = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X_{red}$
$ X_{red}' = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X_{red}$
$ X_{red}' = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X_{red}$

更新することで，以下の列ベクトルが得られるとします．

X'_{red}=
\begin{eqnarray}
\left(
\begin{array}{cccc}
X'_{0,red} \\\
X'_{1,red}  \\\
X'_{2,red}  \\\
X'_{3,red}  \\\
X'_{4,red}  \\\
\end{array}
\right)
,
X'_{green}=
\left(
\begin{array}{cccc}
X'_{0,green} \\\
X'_{1,green}  \\\
X'_{2,green}  \\\
X'_{3,green}  \\\
X'_{4,green}  \\\
\end{array}
\right)
,
X'_{blue}=
\left(
\begin{array}{cccc}
X'_{0,blue} \\\
X'_{1,blue}  \\\
X'_{2,blue}  \\\
X'_{3,blue}  \\\
X'_{4,blue}  \\\
\end{array}
\right)

\end{eqnarray}

これらの特徴量を線型結合で組み合わせて新たな特徴量を作ります．
例えば，こんな感じで作れます．

X_{new} =  0.7 \times X'_{red} + 0.9 \times X'_{green} + (-0.4) \times X'_{blue} 

新たな特徴量を10個作ってみましょう．どのように特徴量を作るかはパラメータとなります．

\displaylines{
Z_0 = \theta_{0,0} \times X'_{red} + \theta_{1,0} \times X'_{green} + \theta_{2,0} \times X'_{blue} \\
Z_1 = \theta_{0,1} \times X'_{red} + \theta_{1,1} \times X'_{green} + \theta_{2,1} \times X'_{blue} \\
\vdots \\
Z_9 = \theta_{0,9} \times X'_{red} + \theta_{1,9} \times X'_{green} + \theta_{2,9} \times X'_{blue} \\
}

これは行列で以下のように書けます．

\displaylines{
(Z_0,Z_1,...,Z_9) = (X'_{red}, X'_{green}, X'_{blue})
\begin{eqnarray}
\left(
\begin{array}{cccc}
\theta_{0,0} & \theta_{0,1}  & \ldots & \theta_{0,9}  \\\
\theta_{1,0} & \theta_{1,1}  & \ldots & \theta_{1,9}  \\\
\theta_{2,0} & \theta_{2,1}  & \ldots & \theta_{2,9}  
\end{array}
\right)
\end{eqnarray}
}

ここで，

\displaylines{
Z = (Z_0,Z_1,...,Z_9)\\\
X' = (X'_{red}, X'_{green}, X'_{blue})\\\
\begin{eqnarray}
\Theta = 
\left(
\begin{array}{cccc}
\theta_{0,0} & \theta_{0,1}  & \ldots & \theta_{0,9}  \\\
\theta_{1,0} & \theta_{1,1}  & \ldots & \theta_{1,9}  \\\
\theta_{2,0} & \theta_{2,1}  & \ldots & \theta_{2,9}  
\end{array}
\right)

\end{eqnarray}
}

と置くと，

Z = X'\Theta

と書けます．

さらに，

\displaylines{
X' = (X'_{red}, X'_{green}, X'_{blue}) \\\
   = (\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X_{red}, \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X_{green}, \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X_{blue})\\\
   = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}(X_{red}, X_{green}, X_{blue})\\
   = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X
}

であるので，

Z = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta

まとめると，
3次元の特徴量$X=(X_{red}, X_{green}, X_{blue})$を，$\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$という式で更新し，
そこに，$3\times 10$の重み行列$\Theta$をかけることで，3次元の特徴量を色々組み合わせて作った10次元の特徴量$Z=(Z_0,Z_1,...,Z_9)$が得られるということです．

もっと一般に，更新前の特徴量をC次元，更新後の特徴量をF次元とすることができ，
$X$は$N\times C$， $\Theta$は$C\times F$, $Z$は$N\times F$ の行列となります．

これにて，GCNの数式を理解することができました．

5.3 層の追加

GCNの更新式

Z = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta

GCNでは，ChebNetにおいて，$K=1$としていました．
この$K$は，どこまでの近傍の情報を使用するか，というパラメータなので，
$K=1$というのは自分自身と隣のノードの情報しか活用していないということです．

もう少し，多くの近傍を拾いたいところです．
GCNの層を重ねることでこれを実現できます．活性化関数を$\sigma$として，

\displaylines{
Z_1 = \sigma (\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta)\\
Z_2 = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}Z_1\Theta \\
}

このように層を重ねると， $Z_1$で自分自身と1次近傍の情報を捉え，$Z_2$で自分自身と1次近傍，2次近傍の情報を捉えることができるようになります．

必要に応じて，層の数を変更したり，$\sigma$を層ごとに変更したりと,層に分けることで，柔軟な設計ができるようになりました．

6. 終わりに

かなり長い記事となってしまいました😓

GCNを理解するために，グラフフーリエ変換とChebNetから学びました．

少しでも参考になれば幸いです．

余談：GCNはグラフ信号処理がベースの手法なのでSpectralな手法に該当します．
　　フーリエ変換せず，近傍ノードの特徴量を活用する手法はSpatialな手法と呼ばれています．GraphSAGEなどのSpatialな手法の方が直感的でわかりやすいので，GCNを学んだ後だと，簡単に思えるかもしれません．

おすすめの記事

グラフニューラルネットワーク(GNN)徹底解説！用途と仕組みからPyGでの実装まで...日本語でかなり詳しくGNNが解説されていておすすめ．

PyTorchで学ぶGraph Convolutional Networks...PyTorchによる実装が学べる．