この記事の目標

GCNの数式

Z = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta

をきちんと理解すること．

この数式が導かれる流れを追っていきます．
そのためにはグラフフーリエ変換やChebNetを学ぶ必要があります．

前提知識

・グラフに関する基本的な知識
　ノード，エッジ，隣接行列，次数行列
・行列の固有値分解
・フーリエ変換
・ニューラルネットワークに関する知識
　・活性化関数
　・誤差逆伝搬法　など...

1. グラフ深層学習とは

ざっくり言うと，グラフ構造から上手いこと情報を抽出する技術です．
様々なグラフ深層学習の手法が提案されていますが，この記事ではその中でも特別に重要なGCNを取り上げます．
GCNの論文：Kipf, T. et al. "Semi-Supervised Classification with Graph Convolutional Networks"(2017)

2. グラフ深層学習ができること

主要なタスクを紹介します．
以下の図では，ノードの特徴量を示していませんが，一般的にはグラフ構造と共にノード特徴量を入力します．
特徴量の例としては，次に紹介するCitation Networkの場合，論文に出てくる単語のword embeddingの平均などが考えられます．

・ノードの分類...ノードのラベルを当てる．
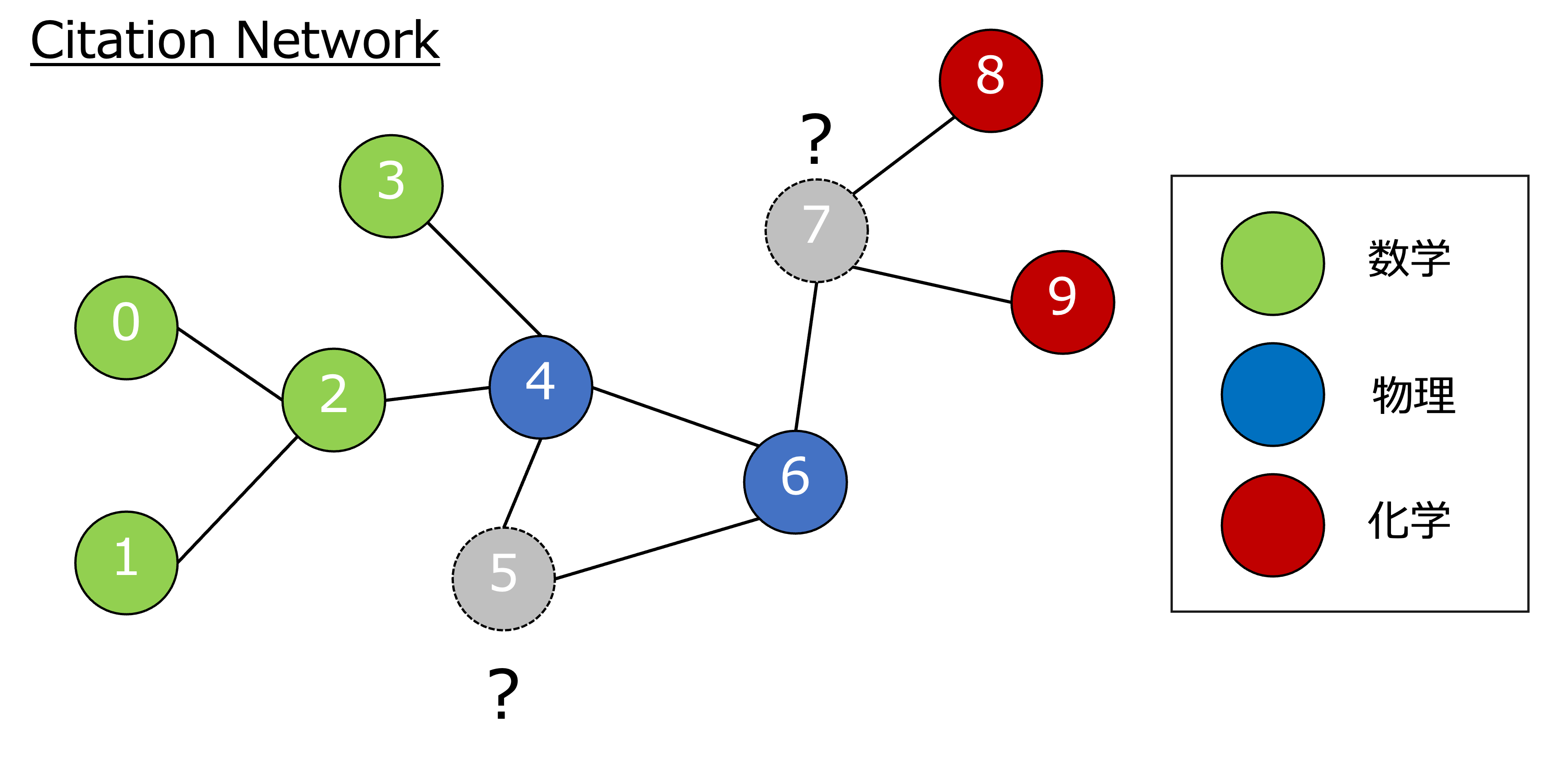
下図のCitation Network（論文をノード，論文の引用関係をエッジとしたグラフ）では，インデックス5,7のラベルが数学，物理，化学のどのジャンルに属するかを当てる問題

・link predciton...ノード間のエッジを当てる．
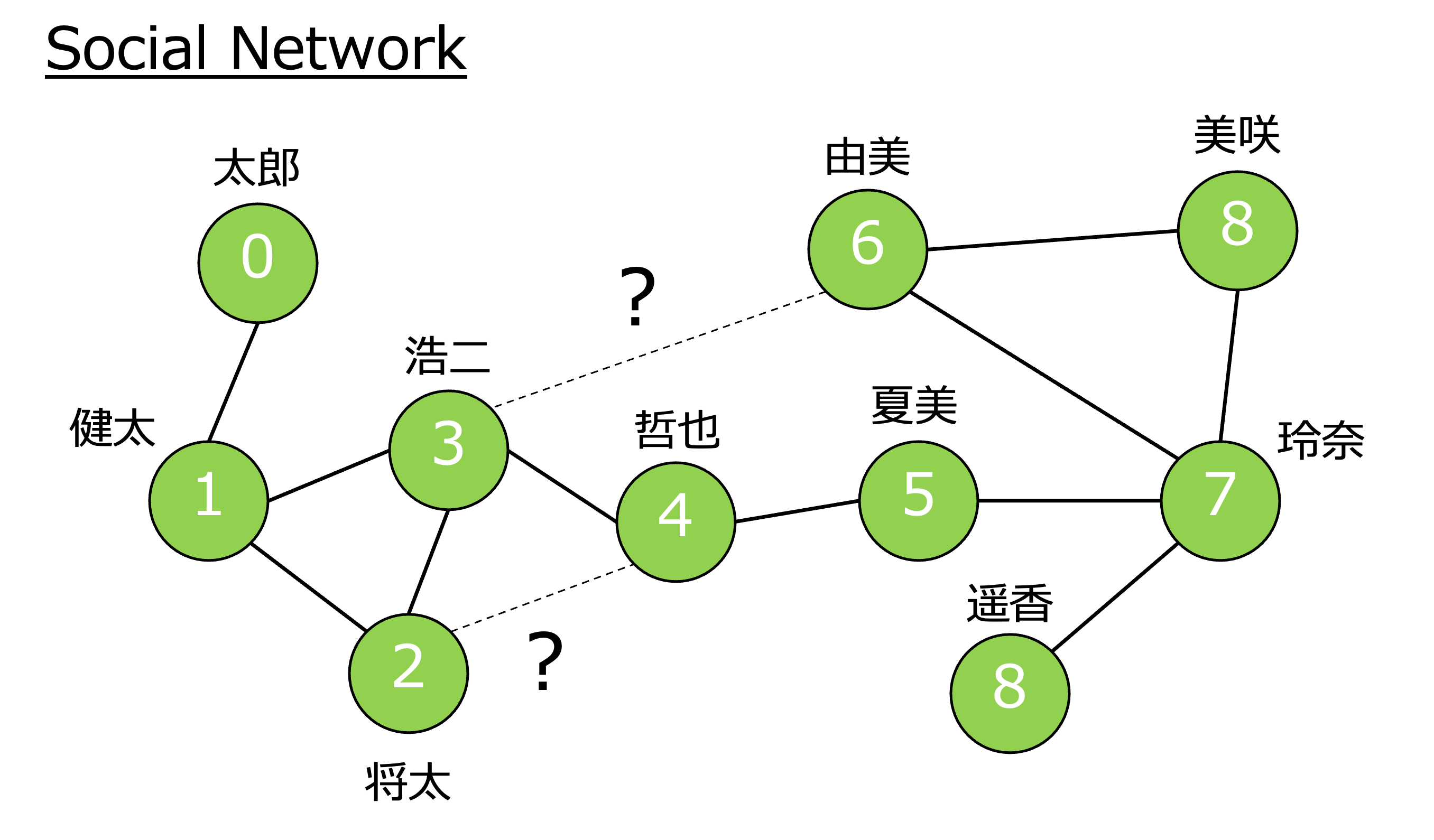
下図のSocial Network（ユーザーをノード，友人関係をエッジとしたグラフ）では，浩二さんと由美さん，将太さんと哲也さんが友人かそうでないかを判定する問題

・graph classfication...グラフのラベルを当てる．
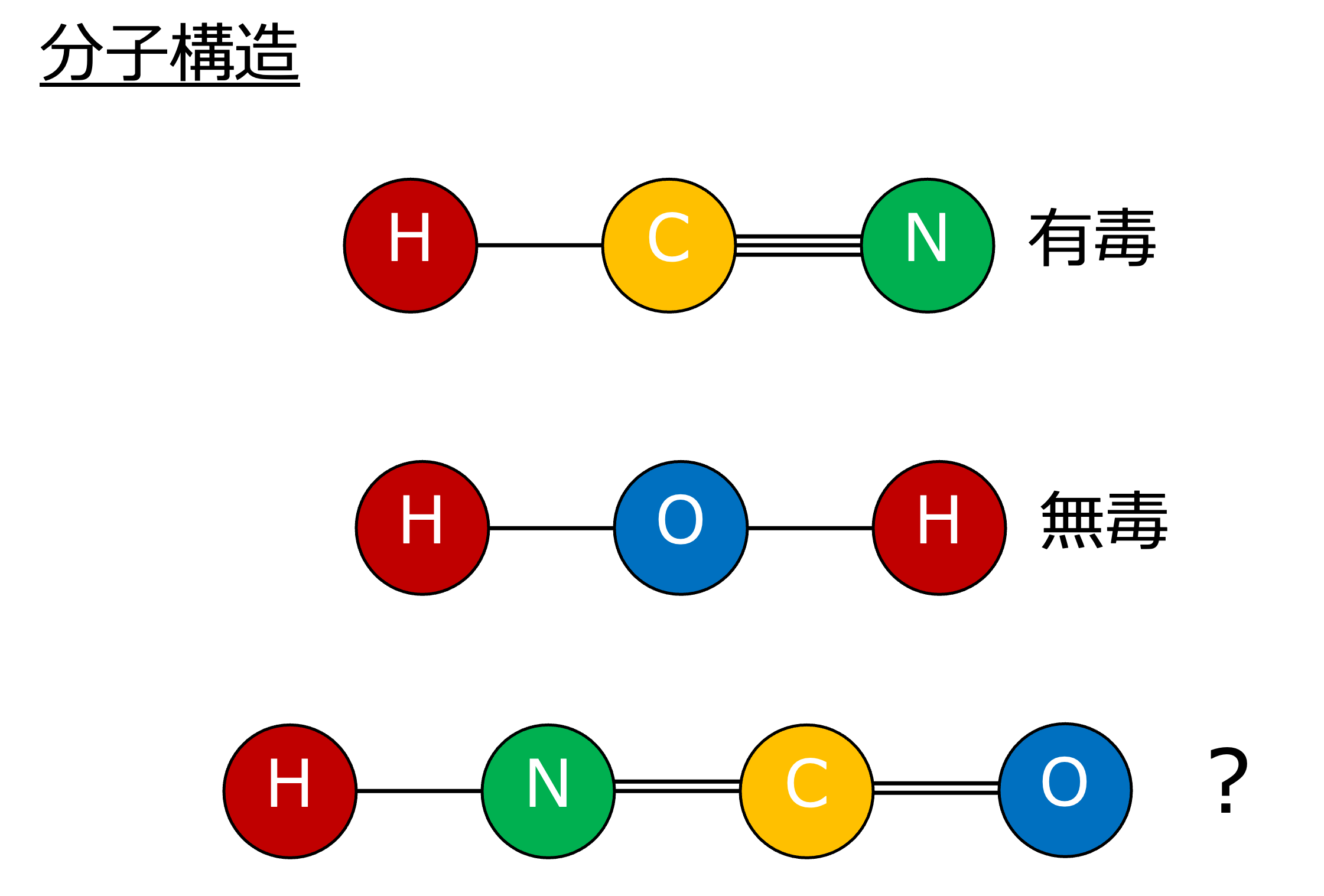
下図の分子構造では，HNCOが有毒か無毒かを当てる問題（実際には，もっと複雑な構造を持つ分子を扱います．）

3. グラフフーリエ変換を理解する

以下では，このグラフを例に考えます．

グラフフーリエ変換では，以下のようなグラフ信号を周波数に分解して解析することが目標です．

3.1 フーリエ変換

3.1.1 フーリエ変換の式

グラフフーリエ変換の前にフーリエ変換について簡単におさらいします．
連続時間信号のフーリエ変換と逆フーリエ変換は以下の式で表されます．
$$
\ F(\omega) = \int_{-\infty}^{\infty} f(t) \cdot e^{-j\omega t} dt
$$
$$
\ f(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) \cdot e^{j\omega t} d\omega
$$

この計算によって，時間領域から周波数領域に変換できます．
これによって周波数解析や信号のフィルタリングなどが可能になります．

3.1.2 フーリエ変換を利用したフィルタリング

フィルタリングの例を見てみます．
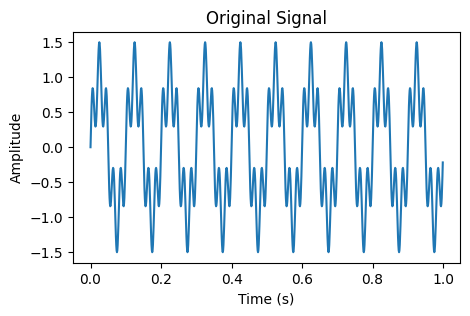
signal_1 = $sin(2\pi ×10t)$, signal_2 = $ sin(2\pi ×50t)$です．
それぞれ，周波数が10Hzと50Hzのsin波です．

これらの信号を足すとこのようになります．

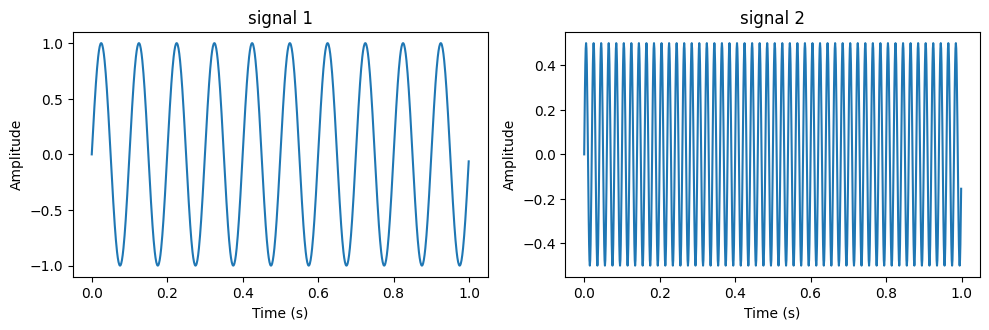
ローパスフィルタを通すことで，この信号から高周波(50Hz)の成分を除去し，低周波(10Hz)の成分を取り出すことができます．

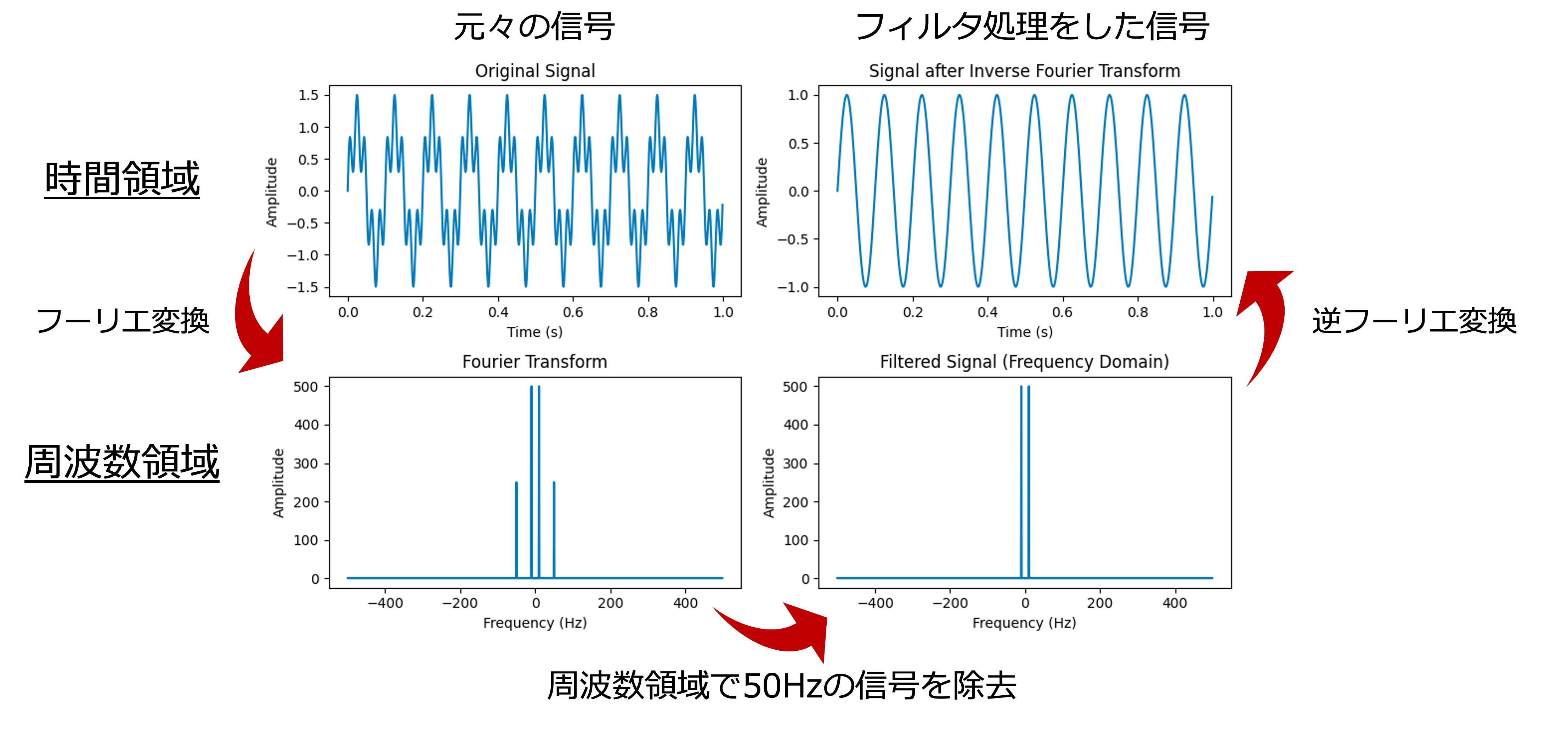
ここで，重要なのは時間領域でなく，周波数領域で処理を行っていることです．

3.2 グラフフーリエ変換への準備

3.2.1 グラフラプラシアン

隣接行列を$A$,次数行列を$D$としたとき，グラフラプラシアンLは
$$
L=D-A
$$
と定義されます．

このグラフラプラシアンにはグラフに関する情報が詰まっていると考えられます．

具体例を見てみましょう．

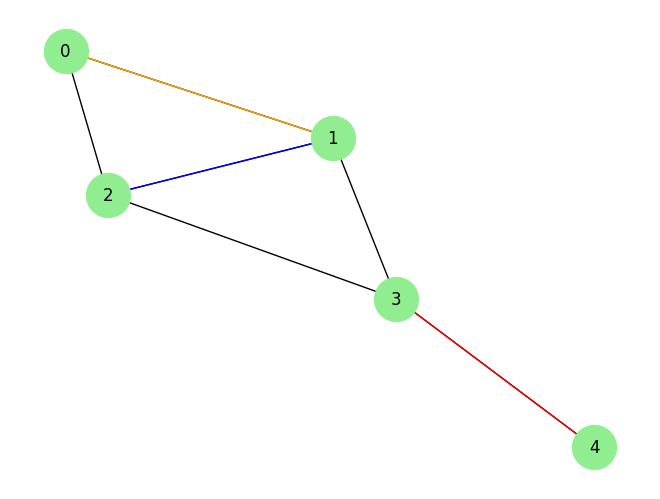
隣接行列$A$

[[0, 1, 1, 0, 0], 
 [1, 0, 1, 1, 0], 
 [1, 1, 0, 1, 0], 
 [0, 1, 1, 0, 1], 
 [0, 0, 0, 1, 0]])

次数行列$D$

[[2, 0, 0, 0, 0]
 [0, 3, 0, 0, 0]
 [0, 0, 3, 0, 0]
 [0, 0, 0, 3, 0]
 [0, 0, 0, 0, 1]]

グラフラプラシアン$L$ ．無向グラフの場合，$L$は対称行列となります．

[[ 2, -1, -1,  0,  0],
 [-1,  3, -1, -1,  0],
 [-1, -1,  3, -1,  0],
 [ 0, -1, -1,  3, -1],
 [ 0,  0,  0, -1,  1]]

ついでに，正規化グラフラプラシアン$\mathcal{L}$についても説明しておきます．
正規化グラフラプラシアン𝓛は，
$$
\mathcal{L} = D^{-\frac{1}{2}}LD^{-\frac{1}{2}} = I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
$$
で定義されます．

この計算を行うことで，エッジの重みを適切に調整することができます．
この意味を先ほどの例を使用して考えてみましょう．

次数行列$D$（再掲）

[[2, 0, 0, 0, 0]
 [0, 3, 0, 0, 0]
 [0, 0, 3, 0, 0]
 [0, 0, 0, 3, 0]
 [0, 0, 0, 0, 1]]

次数行列の$-\frac{1}{2}$乗$D^{-\frac{1}{2}}$
各対角要素$x$について，$x^{-\frac{1}{2}}=\frac{1}{\sqrt{x}}$を計算するだけです．
例えば，2なら$\frac{1}{\sqrt{2}}=0.707...$となり，3なら$\frac{1}{\sqrt{3}}=0.577...$となります．
値が大きいほど,${-\frac{1}{2}}$乗の値が小さくなることに注意しましょう．

[[0.70710678, 0.        , 0.        , 0.        , 0.        ],
 [0.        , 0.57735027, 0.        , 0.        , 0.        ],
 [0.        , 0.        , 0.57735027, 0.        , 0.        ],
 [0.        , 0.        , 0.        , 0.57735027, 0.        ],
 [0.        , 0.        , 0.        , 0.        , 1.        ]])

グラフラプラシアン$L$（再掲）

[[ 2, -1, -1,  0,  0],
 [-1,  3, -1, -1,  0],
 [-1, -1,  3, -1,  0],
 [ 0, -1, -1,  3, -1],
 [ 0,  0,  0, -1,  1]]

正規化グラフラプラシアン$\mathcal{L}$

[[ 1.        , -0.40824829, -0.40824829,  0.        ,  0.        ],
 [-0.40824829,  1.        , -0.33333333, -0.33333333,  0.        ],
 [-0.40824829, -0.33333333,  1.        , -0.33333333,  0.        ],
 [ 0.        , -0.33333333, -0.33333333,  1.        , -0.57735027],
 [ 0.        ,  0.        ,  0.        , -0.57735027,  1.        ]]

グラフラプラシアンと正規化グラフラプラシアンを見比べてみると，正規化グラフラプラシアンでは，対角成分が全て1になっており，非対角成分ではグラフラプラシアンでは−1だった値が変化していることに気づきます．

$$
\mathcal{L} = D^{-\frac{1}{2}}LD^{-\frac{1}{2}} = I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
$$

ノード$i,j (i \neq j)$にエッジがある場合，

$$
\mathcal{L}[i,j] = \mathcal{L}[j,i] = \frac{-1}{\sqrt{ノードiの次数}\sqrt{ノードjの次数}}
$$
となります．

よって，次数の高いノードに関係するエッジほど値が小さくなります．
つまり，次数の高いノード間を繋ぐエッジほど重みが小さく，次数の低いノード間を繋ぐエッジほど重みが大きくなります．

先ほどのグラフをもう一度見てみましょう．

ノード1（次数3）,ノード2（次数3）間のエッジは$\mathcal{L}[1,2]=-0.333...$で，
ノード0（次数2）,ノード1（次数3）間のエッジは$\mathcal{L}[0,1]=-0.408...$で，
ノード3（次数3）,ノード4（次数1）間のエッジは$\mathcal{L}[3,4]=-0.577...$となっており，
次数の高いノード間を繋ぐエッジほど重みが小さく，次数の低いノード間を繋ぐエッジほど重みが大きくなることが確認できました！

3.3 グラフフーリエ変換

・グラフ信号処理の基礎理論と最近の成果
・グラフ信号処理のすゝめ
・新しい信号処理の教科書 ―信号処理の基本から深層学習・グラフ信号処理まで―
これらの資料を参考にしました．

まず，グラフフーリエ変換と逆グラフフーリエ変換の式を載せます．
$$
{F}(\lambda_i) = \sum_{k=0}^{N-1} f(k) \cdot u^*_{\lambda_i} (k)
$$

$$
f(k) = \sum_{i=0}^{N-1} {F}(\lambda_i) \cdot u_{\lambda_i}(k)
$$

となります．

GCNの前にこの数式の意味を理解する必要があります．ゆっくり見ていきましょう．

3.3.1 グラフラプラシアンの固有値分解

ノードの数を$N$とします．
このグラフラプラシアン$L$を固有値分解すると，
固有ベクトル$u_1,u_2,...,u_N$と，固有値$\lambda_1,\lambda_2,...,\lambda_N$ が得られます．

グラフフーリエ変換ではグラフラプラシアンの固有値と固有ベクトルが重要になります．

具体例です．先ほどのグラフを使用します．

グラフラプラシアン$L$（再掲）

[[ 2, -1, -1,  0,  0],
 [-1,  3, -1, -1,  0],
 [-1, -1,  3, -1,  0],
 [ 0, -1, -1,  3, -1],
 [ 0,  0,  0, -1,  1]]

このグラフラプラシアンを固有値分解すると，
固有値は，

# λ_1      λ_2      λ_3      λ_4      λ_5     
 [0.     , 0.82991, 2.68889, 4.     , 4.48119 ]

となり，
固有値に対応する固有ベクトルは，

# U
# u_1       u_2      u_3      u_4      u_5      
[[-0.44721  0.43753 -0.70308 -0.       0.338  ]
 [-0.44721  0.25597  0.24217  0.70711 -0.41932]
 [-0.44721  0.25597  0.24217 -0.70711 -0.41932]
 [-0.44721 -0.13802  0.53625 -0.       0.70242]
 [-0.44721 -0.81146 -0.31752  0.      -0.20177]]

となります．

ちなみに，固有値分解は，numpy.linalg.eig(matrix)で簡単に行えます．numpy.linalg.eig

3.3.2 グラフフーリエ変換の考え方

グラフラプラシアンを固有値分解して得られた
固有ベクトル$u_1,u_2,...,u_N$と固有値$\lambda_1,\lambda_2,...,\lambda_N$が何を意味するかを考えていきます．

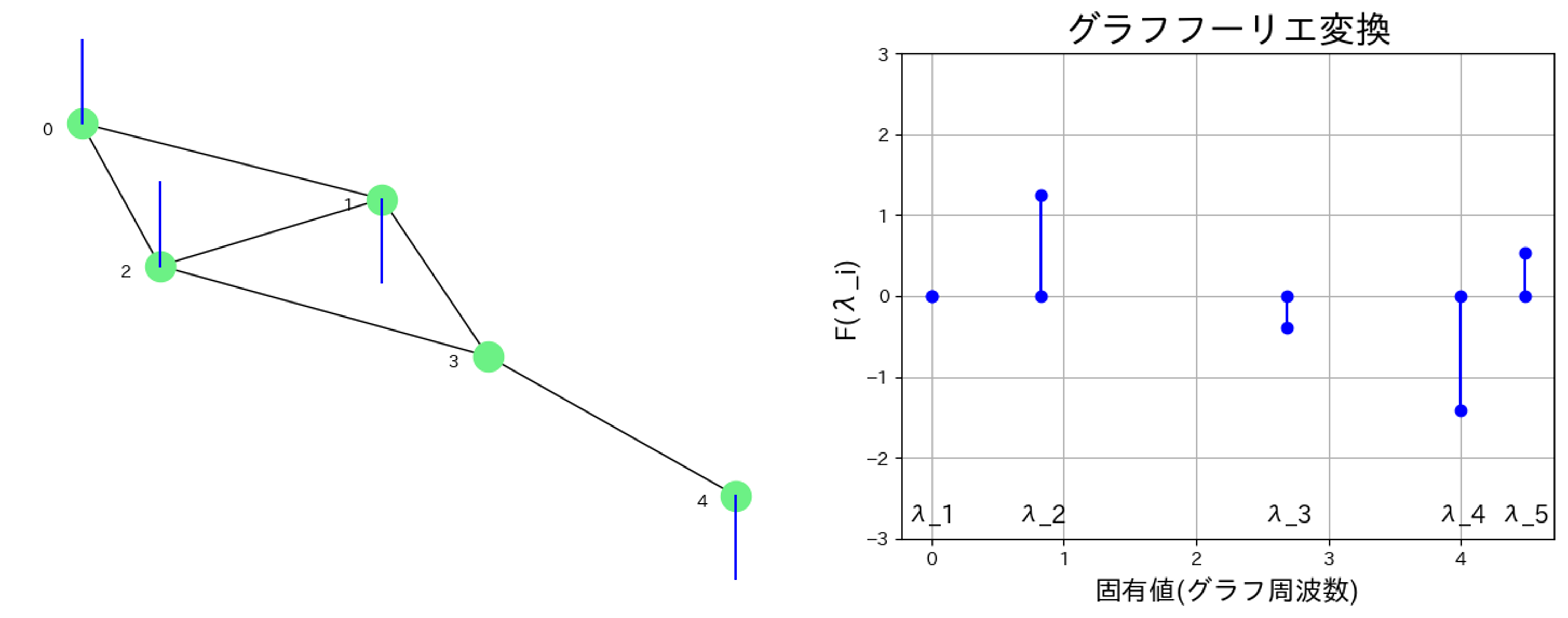
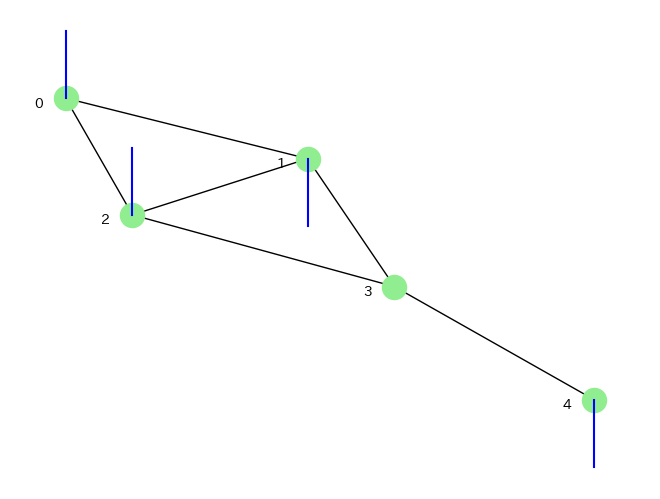
まず固有ベクトルを，グラフのノードに対応させてプロットしてみます．
グラフから上に伸びている信号は正，下に伸びている信号は負を表します．

エッジで繋がったノード間の成分の変化に注目して下さい．
固有値が小さいほど変化が小さく，固有値が大きいほど変化が大きいことがわかります．
特に，固有値$\lambda_1$では全ての成分が同じで変化がなく，固有値$\lambda_5$では正負の変化が激しいことがわかると思います．

＜重要＞
グラフラプラシアンの固有値$\lambda_1,\lambda_2,...,\lambda_N$ ...グラフ周波数
グラフラプラシアンの固有ベクトル$u_1,u_2,...,u_N$...フーリエ基底
とすることができます．　
無向グラフの場合，グラフラプラシアンは実対称行列であるため，固有ベクトル$u_1,u_2,...,u_N$は正規直交基底となリます．
つまり，内積$
\text{$u_i^T*u_j= $}
\begin{cases}
\text{1 ($i = j$)} \\
\text{0 ($i \ne j$)}
\end{cases}
$を満たします．
証明はここにあります．対称行列の固有値と固有ベクトルの性質の証明

これでグラフフーリエ変換の式を理解することができます．
$$
{F}(\lambda_i) = \sum_{k=0}^{N-1} f(k) \cdot u_{\lambda_i} (k)
$$

グラフフーリエ変換では，$u_1,u_2,...,u_N$というベクトルを基底としてグラフ信号を分解します．
つまり，解析したいグラフ信号が$u_1,u_2,...,u_N$という基底をそれぞれどの程度持っているかというのを調べます．

例えば，上の図において，$u_1$の割合が大きいグラフ信号は成分の変化が少なく滑らかで，$u_5$の割合が大きいグラフ信号は成分の変化が大きく滑らかでないといったことがわかるようになります．

実際に例を見た方がわかりやすいと思います．

グラフ信号とグラフフーリエ変換を施した結果を載せています．
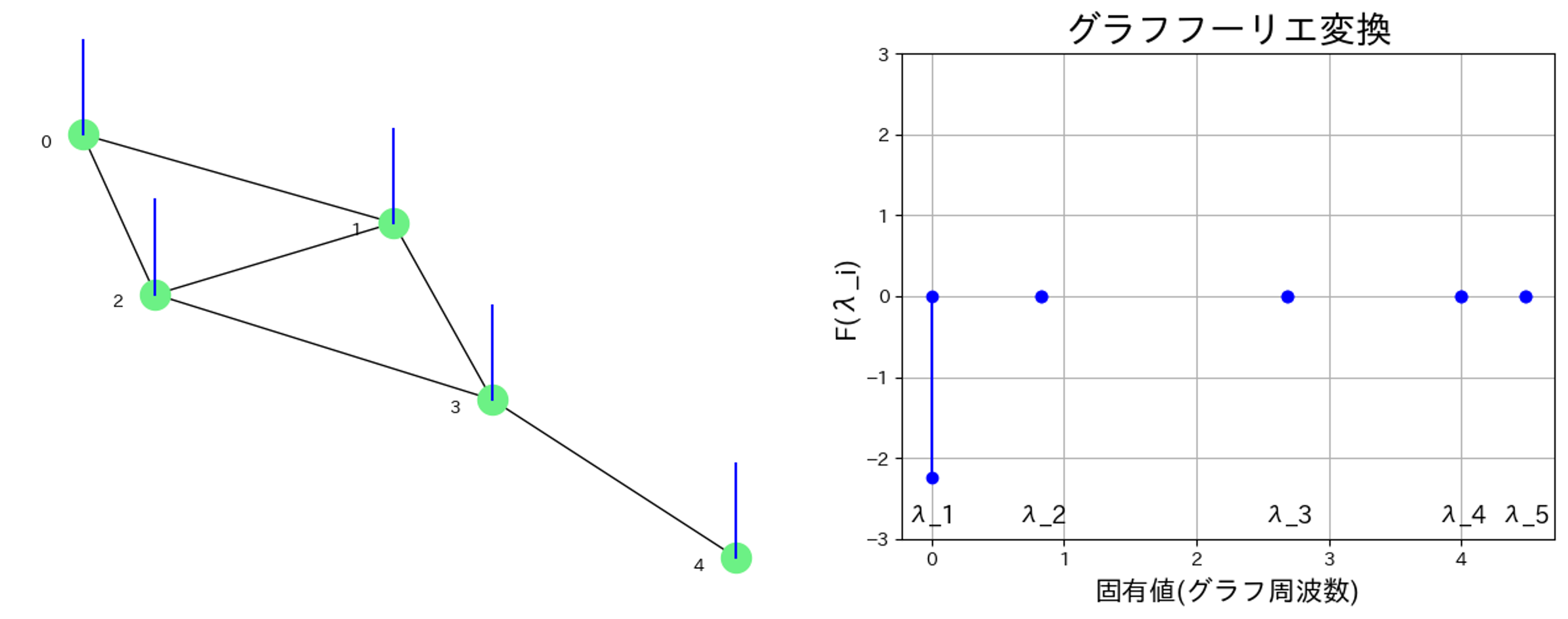
（信号の値は-1,0,1の3種類に制限しています．）

例1：このように変換を行うことができます．

例2：信号の値に変化がない場合，グラフ周波数が0の成分$F(\lambda_1)$以外は0になっています．

例3：信号の値の変化が激しい場合は，グラフ周波数が高い成分$F(\lambda_5)$が大きいことがわかります．

例4：もっと大きなグラフで試すとこんな感じです．

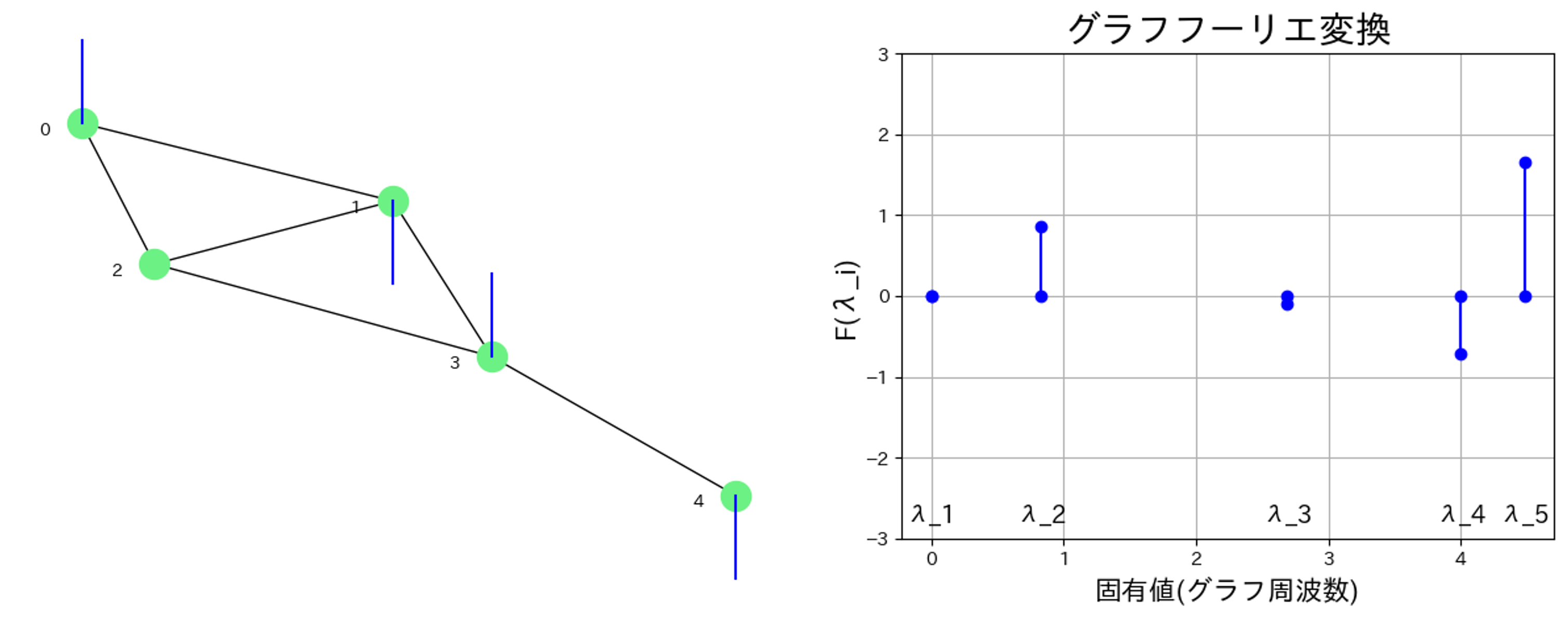
グラフフーリエ変換によって，グラフ信号を周波数解析することが可能になりました！

続き

こちらです→きちんと理解する Graph Convolution Networks (2)

きちんと理解する Graph Convolution Networks (1)