ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは気軽にフォローしてください！

PyTorchで学ぶGraph Convolutional Networks

この記事では近年グラフ構造をうまくベクトル化(埋め込み)できるニューラルネットワークとして、急速に注目されているGCNとGCNを簡単に使用できるライブラリPyTorch Geometricについて説明する。応用分野は生物学から、渋滞予測、レコメンダーシステムまで幅広い。
本記事はGCN生みの親のブログ記事とPyTorch Geometricの公式チュートリアルをかなり参考にしております。

読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります！よろしくお願いします！

1. Graph Convolutional Networksとは？

1.1 そもそもグラフとは？

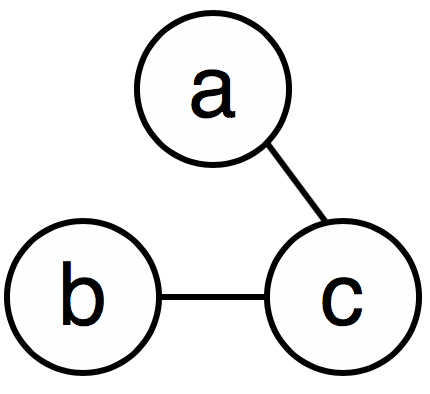
ノードとエッジで定義される。折れ線グラフやヒストグラムといった類のグラフではないことに注意。具体例では、Facebookの友達関係(人がノードで友人関係がエッジ)や酵素の構造(原子がノードで結合関係がエッジ)など。(ここでは重みなし無向グラフとします。)

それぞれがそれぞれの特性を持つ。
またグラフは数学的に行列で表すことができ、このGCNでは隣接行列と特徴行列の2つを用いる。

• 隣接行列: ノードとノードの結合関係を表す行列
• 特徴行列: 各ノードの特徴ベクトルを表す行列

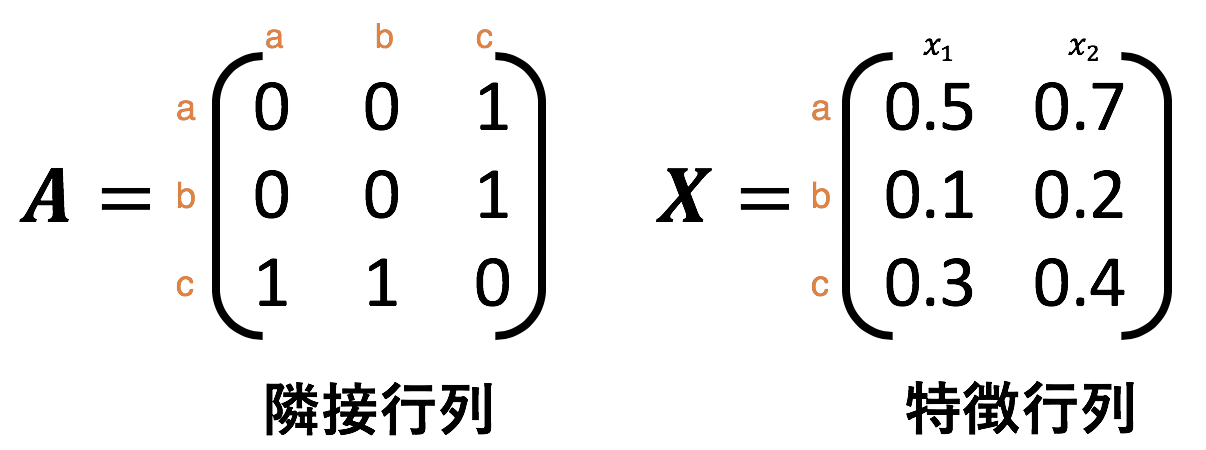
先ほどの図の例を隣接行列と特徴行列で表すと以下になる。
オレンジ色の文字が各ノードを表す。例えば、隣接行列において1行目の3列目はノードaとノードcが接続されているため1が入っている。特徴行列は $x_1, x_2$ がそれぞれ特徴を示している。

1.2 GCNとは？

1.2.1 概要

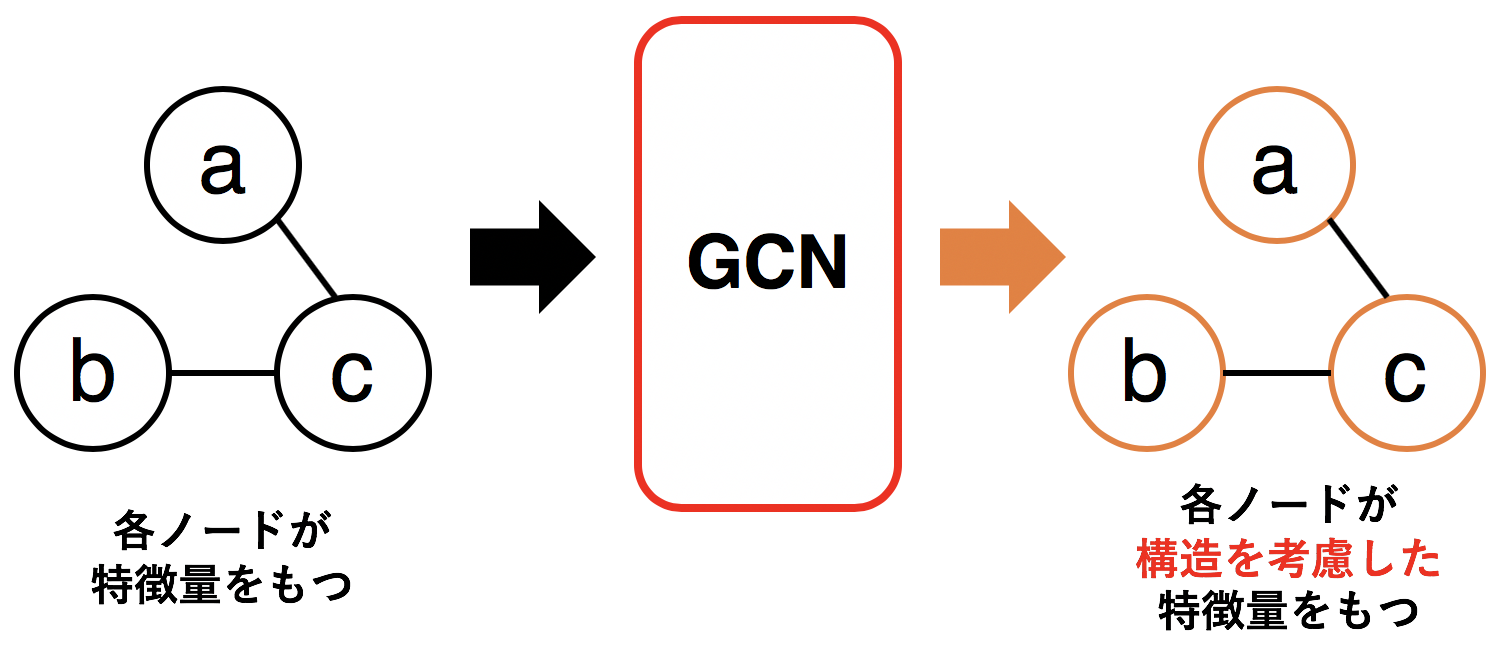
GCN(=Graph Neural Networks)とはグラフ構造をしっかりと加味しながら、各ノードを数値化(ベクトル化、埋め込み)するために作られたニューラルネットワーク。
GCNのゴールは 構造を加味して各ノードを数値化する というところにある。

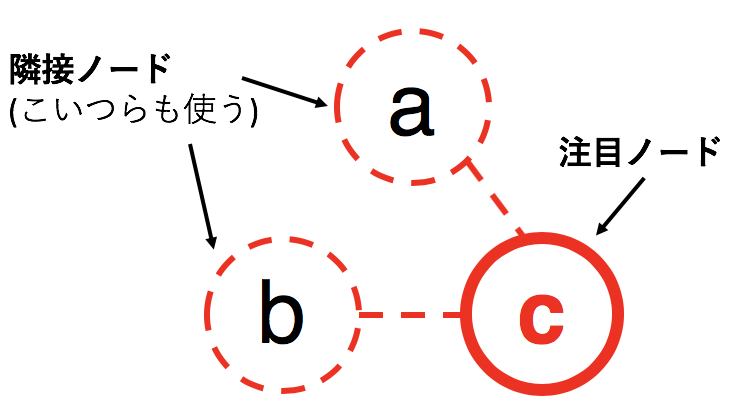
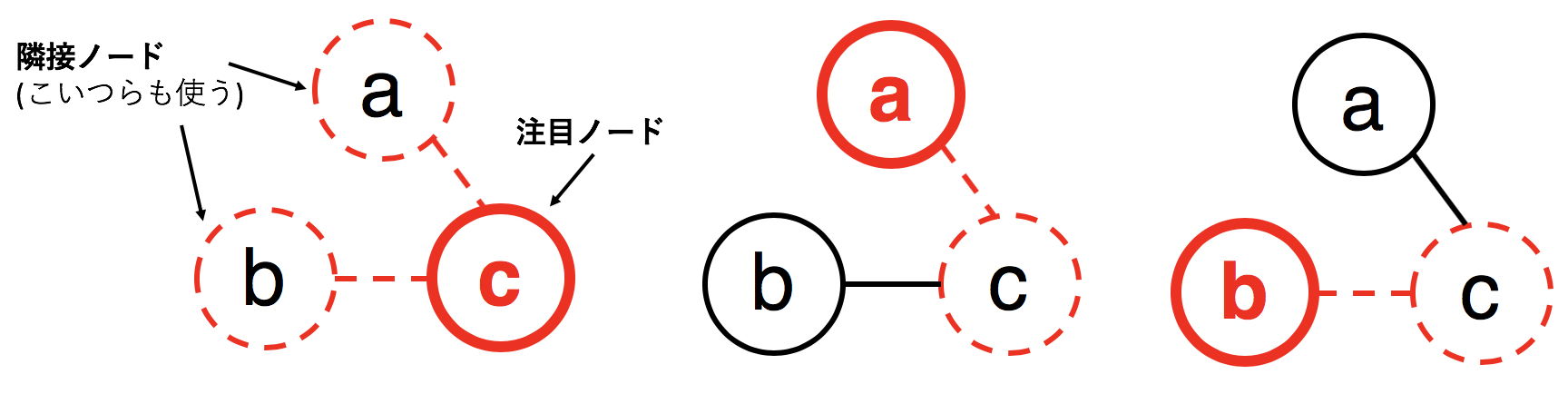
ここで、構造を加味しながらというのはつまり いま注目しているノード(数値化したいノード)がどういったノードとくっついているかを加味しながら 数値化していくと言える。
具体的にノードcについて考えると以下の図。

同様に他のノードに対しても色付けを行うと以下の図。

これを全ノードに対して行う。
GCNは一言で言えば、あるノードの隣接たちを見て埋め込むネットワーク と言える。

GCNは2種類の行列を入力とし、1つの行列を出力する。

• 入力
  • 隣接行列 $\mathbf{A} \in \mathbb{R}^{n\times n}$ : どのノードとどのノードが繋がっているかを表す行列。
  • 特徴行列 $\mathbf{F}_{in} \in \mathbb{R}^{n\times |F|}$: 各ノードの特徴ベクトルを表す行列。
• 出力
  • 潜在行列 $\mathbf{H}_{out} \in \mathbb{R}^{n\times |H|}$: 各ノードの潜在表現ベクトルを表す行列。(GCNによる変換済)

1.2.2 数式

早速だが、GCNを数式で表すと以下になる。

$$
\mathbf{H}^{(l+1)} = f(\mathbf{H}^{(l)}, \mathbf{A})
$$

ただし、$H^{(0)}=X$ である。

これでGCN自体の定義は終わりなのだが、ちょっと意味がわからないので具体例で見てみる。
ここで活性化関数をReLUとした1層のGCNを例にとってみる。先ほどのGCNの図を再掲する。ここで活性化関数はReLUが使われていると仮定している。

これを数式で表すと、

$$
f(H^{(0)}, A) = f(X, A) = \mathrm{ReLU}(AX\cdot W)
$$

となる。$W$ は通常のニューラルネットワークと同じく、重みである。 $A, X$ はそれぞれ隣接行列および特徴行列(入力)である。ここで $AX$の意味について考えてみよう 。
これは実際にAXを計算してみるとわかるのでやってみる。
再び以下のグラフを使う。

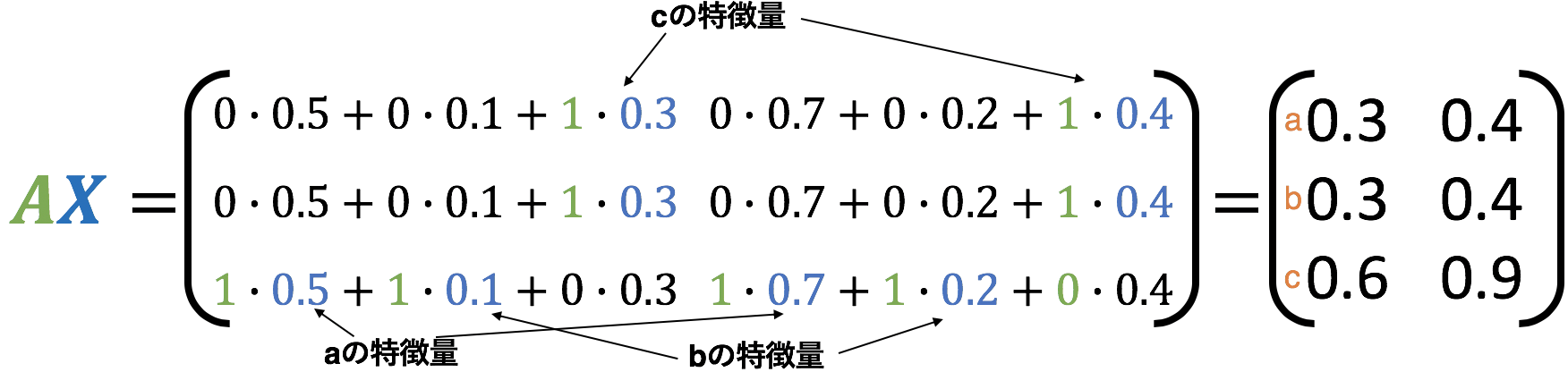
$AX$ を計算してみる。以下の図で隣接行列が1となっているところだけ色付けした。

たとえば、ノードcの計算結果を見てみると、隣接しているaとbの元々の特徴量を足し合わせた得られていることがわかる。
このことから、$AX$ つまり 隣接行列 $\times$ 特徴行列はあるノードと繋がっているノードたちの特徴量を足し算したもの　であることがわかる。$AX$によって周りのノードたちを考慮した特徴量を獲得でき、あとはそれに通常のニューラルネットワークのように重み$W$を掛け算し、非線形の活性化関数 $\mathrm{ReLU}$ を適用しているだけである。

現時点である程度強いのだが、実は問題点が2つある。その2つを解決したものこそが一般的に使われているGCNである。それでは問題点とその解決方法を見ていこう。

1.2.3 問題点と解決方法

1. 自身ノードの情報が入っていない。(近傍ノードの情報のみ)
2. $AX$ の行列の乗算のせいで 各ノードごとにスケールが大きく異なってしまう。

この2つの問題点を解決する方法はいたって簡単。

1. 隣接行列$A$に単位行列$I$を足して $\hat{A}=A+I$ とすることで自身ノードの情報も加える。ここで$I$とは対角成分が1でそれ以外0の行列のこと。
2. 隣接行列 $\hat{A}$ を $\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$ として正規化。つまり各行の合計値を1としている。ここで、$\hat{D}$ は $\hat{A}$ の次数行列。次数行列とは、対角成分が各ノードの次数でそれ以外0の行列のこと。

こうして最終的なGCNの式は以下の式となる。

$$
f(H^{(0)}, A) = \mathrm{ReLU}(\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}X\cdot W)
$$

1.3 GCNの例

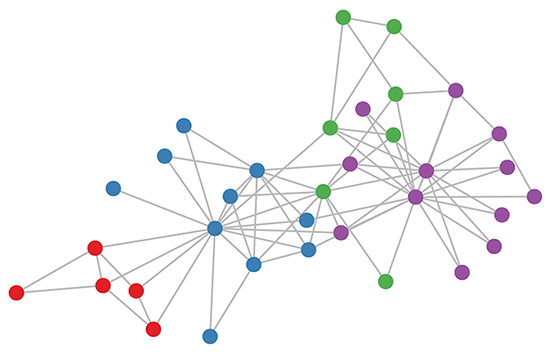
上の式で実現されたGCNを使って、複雑ネットワーク界隈のMNIST的存在である空手クラブネットワーク(Zachary (1977))の各ノードをベクトル空間に埋め込んでみる。まずは元々のネットワークは以下の図。ノードが空手クラブの部員、エッジが友人関係を示している。

Image Credit: Kipf, T. et al. (2017)

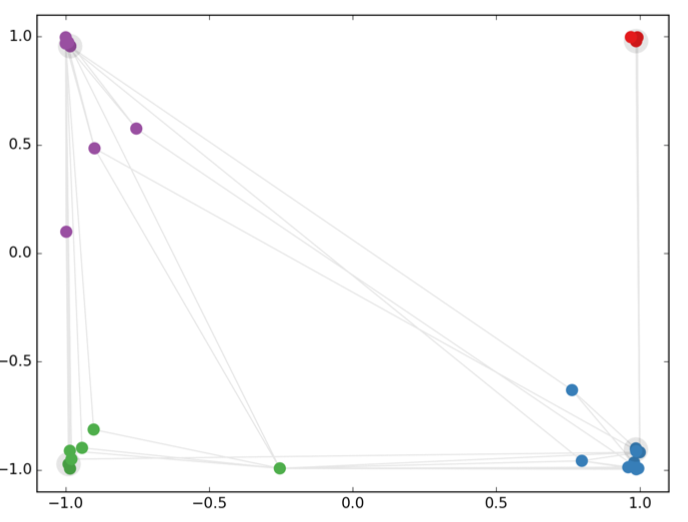
同一色は同一クラスターを表しており、4つのクラスターがあることがわかる。これを3層GCNを使って各ノードを二次元空間に埋め込んだ結果が以下。同じクラスター同士は近く、異なるクラスター同士は遠くに埋め込まれており、うまくいっている ことがわかる。

Image Credit: Kipf, T. et al. (2017)

1.4 なぜGCNがうまくいくのか。

ここは主題であるPyTorch Geometricから離れてしまうので、詳しくは参考文献を当たって欲しいが簡単にだけ説明すると、GCNは、Weisfeiler-Lehmanアルゴリズムに①パラメータを持たせ、②微分可能性を追加した特殊ケースと捉えることができるため うまくいっていると考えられる。

(Weisfeiler-Lehmanアルゴリズムではノードの潜在表現は $\mathrm{hash}(AX)$ という任意のハッシュ関数を用いて獲得するが、GCNでは $\mathrm{ReLU}(\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}X\cdot W)$ というパラメトリックでかつ微分可能な関数を用いていると考えられる。)

2. GCNを使ってみよう

PyTorch Geometric(PyG)で実際にGCNに触れてみる。PyGのチュートリアルを順にやっていく。
ノートブックを日本語のコメント豊富にこちらのGithubにあげましたのでお手元で実行しながらお読みいただければ、より理解が深まるかと思います。

ここでは インストール と実際に GCNレイヤーを使う ところのみ紹介。より詳しいデータの準備などはGithub先のノートブックを参照してください。

2.1 PyGのインストール

pytorchのバージョンが1.2.0以上であることを確かめてください。pytorchが入っていなければ

$ pip install torch

でインストールしましょう。

$ python -c "import torch; print(torch.__version__)"
>>> 1.2.0

続いてPyTorch Geometricをインストールしてみましょう。

$ pip install --verbose --no-cache-dir torch-scatter
$ pip install --verbose --no-cache-dir torch-sparse
$ pip install --verbose --no-cache-dir torch-cluster
$ pip install --verbose --no-cache-dir torch-spline-conv (optional)
$ pip install torch-geometric

2.2 グラフデータ

PyGにベンチマーク的なデータセットは用意されているので、今回は 論文の被引用ネットワークを示すCoraデータセット を使う。Coraは2708もの論文を含み、それぞれの論文が7つのクラスに分けられている。このデータセットを使って、各ノード(論文)のカテゴリを予測 する。

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/tmp/Cora', name='Cora')

2.3 GCNレイヤーを使ってみる。

基本的にPyTorchと同じ記法なので、PyTorchを触ったことある方なら特に問題はないかもしれない。PyTorchがわからない場合は公式チュートリアル(英語)がわかりやすい。

NetクラスにNNの構造とforwardメソッドを記入。その中で単純に GCNConv を呼び出すだけ。

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

2.4 GCNの学習

学習はPyTorchといたって同じだが、念のため丁寧に触れておく。
学習の時の手順は以下の5つをエポック回だけ繰り返す。

1. optimizerの勾配初期化
2. モデルからの予測値を得る
3. 予測値と正解値で損失をとる
4. 損失のパックプロップ
5. optimizerによるパラメータ更新

つまり、

1. 勾配初期化
2. 予測値
3. 損失
4. バックプロップ
5. 更新

で、コードで書けば、

1. optimizer.zero_grad()
2. output=model(input)
3. loss=Loss(output, target)
4. loss.backward()
5. optimizer.step()

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train() #モデルを訓練モードにする。
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

これにて学習が完成する。

2.5 評価

model.eval() #モデルを評価モードにする。
_, pred = model(data).max(dim=1)
correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print('Acc: {:.4f}' .format(acc))

>>> Accuracy: 0.8150

これで評価までできた。
このような簡単なネットワークでもノードのクラスをうまく推測できていることがわかる。

より詳しい説明はノートブックをご参照ください。

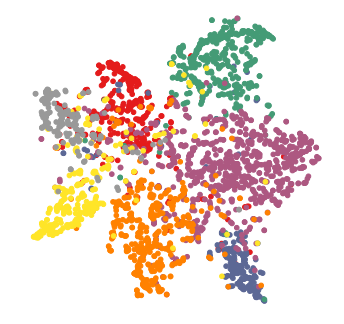
ちなみに、2層GCNを使ってCoraデータセットのノードをベクトル化させt-SNEで可視化すると以下の図のようになり、しっかりと同じクラスのデータたちは集まっていることがわかる。色が各クラスを表している。

Kipf, T. et al. "Semi-Supervised Classification with Graph Convolutional Networks" (2017)

3. まとめと所感

GCNの簡単な説明とPyTorch Geometricの簡単な使い方について紹介した。
さらなる可能性を秘めているであろうGCNについてこれからも注目していきたい。

読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります！よろしくお願いします！

4. 参考

• Kipf, T. et al. "Semi-Supervised Classification with Graph Convolutional Networks" (2017)
  (論文) 現在広く使われるGCNの原型となる論文.

• PyTorch Geometric Documentation
  (英語)PyTorch Geometricの公式ドキュメント

• GRAPH CONVOLUTIONAL NETWORKS
  (英語) GCN生みの親のブログ記事。とてつもなく参考にしています。

• 半教師あり学習_Semi-Supervised Learning (Vol.20)
  半教師あり学習についてわかりやすくまとめてくれている。