目次
以下のこれら記事はPyTorchを使って時系列データの予測をしたい方に向けて書きました.
理論は本や論文をじっくり読む方が良いかと思いましたので,特に実装方法について詳しく書きました.
使用するプログラムの一部は各記事の中で重複しているものもあり,重複した部分を毎回1から説明すると記事が長くなり読みにくいと思うので省略しています.
そのため以下の順番で読み進めていただけると読みやすいかと思います.
- [PyTorch 1.9.0] LSTMを使って時系列(単純な数式)予測してみた
- [PyTorch 1.9.0] LSTMを使っていくつ先の未来まで精度良く予測できるのか検証してみた <- 現在読んでいただいている記事
0. はじめに
LSTMについて勉強していると先の未来を予測すれば予測するほど精度が落ちるという記述をみました.
確かに1個先の未来を予測するよりも10個先の未来を予測する方が難しいというのは直感的にわかります.
ただ2,3個先の未来ならうまくいきそうですし,そのうまくいかない分水嶺ってどこにあるのかということを知りたくなりました.
そこで簡単な時系列データを用いていくつ先の未来までだったら精度良く予測できるのか検証してみました.
いくつか先の未来を予測する方法は主に2つあると考えられます.
1つ目は,学習時に正解ラベルを1つ先の未来の情報ではなく,いくつか先の未来の情報にして学習するという方法です.
2つ目は,正解ラベルを1つ先の未来の情報で学習したモデルを繰り返し使うという方法です.
比較のしやすさからこの記事では2つ目の方法を用いました.
これはmany to many のシーケンスモデルです.
問題設定
sin関数やcos関数のような単純な数式を使って時系列データを生成し,その数式のいくつかの出力を用いて1~9つ先の未来の値を予測する問題を設定しました.
イメージとしては以下の図の通りです.
オレンジ色の点から緑の点を求める問題を設定しました.
精度検証にはRMSEを使いました.
1つ先の未来を予測したときのRMSEの値を基準として,その基準から何パーセントずれているのかで精度を評価しました.
RMSEは,正解ラベルと予測値の二乗平均平方根誤差を計算しています.
この値が小さければ小さいほどうまく当てはまっているモデルを学習できていると言えます.
RMSEについて詳しく知りたい人は以下のサイトが参考になると思います.
1. プログラムの概要
プログラムのほとんどのコードが前回の記事で紹介したコードと同じです.
ただ前回のままだと1つ先の未来しか予測できないのでpred_result_pltの関数内の処理に改変を加えることで,任意の先の未来を予測できるようにしました.
この記事で説明するコードの全体(折りたたんでいるのでこれをクリックして頂けると全体が見られます)
2. プログラムの説明
プログラムの概要の方でも言いましたが,pred_result_pltの関数以外は前回と同じなのでこの関数だけ説明しようと思います.
この関数は,学習したモデルを使って1~任意の先の未来を予測し,正解ラベルと比較する処理を行っています.
`pred_result_plt`の関数のコードの全体(折りたたんでいるのでこれをクリックして頂けると全体が見られます)
def pred_result_plt(self, test_inputs, test_labels, test_times, sequence_length, input_size, pred_step_list):
print('-------------')
print("start predict test!!")
self.net.eval()
preds = [[] for num in range(len(pred_step_list))]
rmses = [0.0 for num in range(len(pred_step_list))]
for i in range(len(pred_step_list)):
for j in range(0, len(test_inputs), pred_step_list[i]):
input = np.array(test_inputs[j]).reshape(-1, sequence_length, input_size)
for k in range(pred_step_list[i]):
if j + k < test_labels.shape[0]:
input_tensor = torch.Tensor(input).to(self.device)
pred = self.net(input_tensor).data.cpu().numpy()
input = np.delete(input, 0, axis=1)
input = np.insert(input, 2, pred[0][0], axis=1)
preds[i].append(pred[0][0])
preds[i] = np.array(preds[i]).reshape(-1)
test_labels = test_labels.reshape(-1)
rmses[i] = np.sqrt(np.sum(np.power((test_labels - preds[i]), 2)) / float(test_labels.shape[0]))
print("pred_step = {}, rmse = {}, rmse_ratio = {}".format(i + 1, rmses[i], (rmses[i] - rmses[0]) / rmses[0]))
#以下グラフ描画
plt_legend_list = ['label']
for i in range(len(pred_step_list)):
plt.plot(test_times, preds[i])
plt_legend_list.append('pred_' + str(pred_step_list[i]))
plt.plot(test_times, test_labels, c='#00ff00')
plt.xlabel('t')
plt.ylabel('y')
plt.legend(plt_legend_list)
plt.title('compare label and preds')
plt.show()
以下のコードはこの引数でいくつ先の未来を予測したいか指定しています.
このプログラムでは1~9つ先の未来を予測したいので[0,1,2,3,4,5,6,7,8,9]の配列を引数として渡します.
前回と違うのは引数にpred_step_listが追加されているところです.
def pred_result_plt(self, test_inputs, test_labels, test_times, sequence_length, input_size, pred_step_list)
以下のコードは,予測した各出力と各RMSEを保存するためのリストを用意する処理を行っています.
preds = [[] for num in range(len(pred_step_list))]
rmses = [0.0 for num in range(len(pred_step_list))]
以下のコードは,先ほどの用意したリストに予測した出力を保存する処理を行っています.
for i in range(len(pred_step_list))のiの最大値は予測したい未来の数です.
1~9つ先の未来を予測したいので9回ループを回しpredsのリストに予測した出力を9回appendします.
for j in range(0, len(test_inputs), pred_step_list[i])のjの最大値はテスト用の入力データの数です.
また3つ目の引数のpred_step_list[i]は予測したい未来の先によって使うテスト用の入力データを変えるためのものです.
例えばi=0つまりpred_step_list[i]=1の時は,普通のforループのように1つ飛ばしでループを回します.
この時使うテスト用の入力データは,[[test0,test1,test2][test1,test2,test3]...[test47,test48,test49]]となります.
次にi=4つまりpred_step_list[i]=4の時は普通のforループとは違い3つ飛ばしでループを回します.
この時4つ飛ばしのため使うテスト用の入力データは,[[test0,test1,test2][test4,test5,test6]...[test43,test44,test45]]となります.
これはなぜこのようなforループの値を飛ばす処理をするのかというと4つ先の未来を予測するときは予測した出力を入力として使いまわすからです.
4つ先の未来を予測するときはまず[test0,test1,test2]の入力データから1つ先の未来のtest3を予測します.(予測したtest3をtest3_predと呼ぶことにします.)
test3_predを使い[test1,test2,test3_pred]という入力データを作り2つ先の未来のtest4を予測します.
これを繰り返し4つ先の未来のtest6まで予測します.
よって次に予測したいのはtest7であり,次に使うテスト用の入力データは[test4,test5,test6]が良く,forループの値を飛ばす処理が必要です.
for k in range(pred_step_list[i])のkの最大値はiの時の予測幅です.
このループの中で予測した値を使いまわす処理を行います.
予測した値を使いまわすため,まずnp.delete(input, 0, axis=1)で入力データの先頭を消去します.
そしてnp.insert(input, 2, pred[0][0], axis=1)で入力データの末尾に予測値を追加します.
for i in range(len(pred_step_list)):
for j in range(0, len(test_inputs), pred_step_list[i]):
input = np.array(test_inputs[j]).reshape(-1, sequence_length, input_size)
for k in range(pred_step_list[i]):
if j + k < test_labels.shape[0]:
input_tensor = torch.Tensor(input).to(self.device)
pred = self.net(input_tensor).data.cpu().numpy()
input = np.delete(input, 0, axis=1)
input = np.insert(input, 2, pred[0][0], axis=1)
preds[i].append(pred[0][0])
以下のコードは,RMSEを計算する処理を行っています.
reshape(-1)でpreds[i]とtest_labels の配列の形を揃えます.
preds[i] = np.array(preds[i]).reshape(-1)
test_labels = test_labels.reshape(-1)
rmses[i] = np.sqrt(np.sum(np.power((test_labels - preds[i]), 2)) / float(test_labels.shape[0]))
print("pred_step = {}, rmse = {}, rmse_ratio = {}".format(i + 1, rmses[i], (rmses[i] - rmses[0]) / rmses[0]))
以下のコードは,正解ラベルと予測した1~9つ先の値を重ねてグラフに表示する処理を行っています.
#以下グラフ描画
plt_legend_list = ['label']
for i in range(len(pred_step_list)):
plt.plot(test_times, preds[i])
plt_legend_list.append('pred_' + str(pred_step_list[i]))
plt.plot(test_times, test_labels, c='#00ff00')
plt.xlabel('t')
plt.ylabel('y')
plt.legend(plt_legend_list)
plt.title('compare label and preds')
plt.show()
3. 実行結果
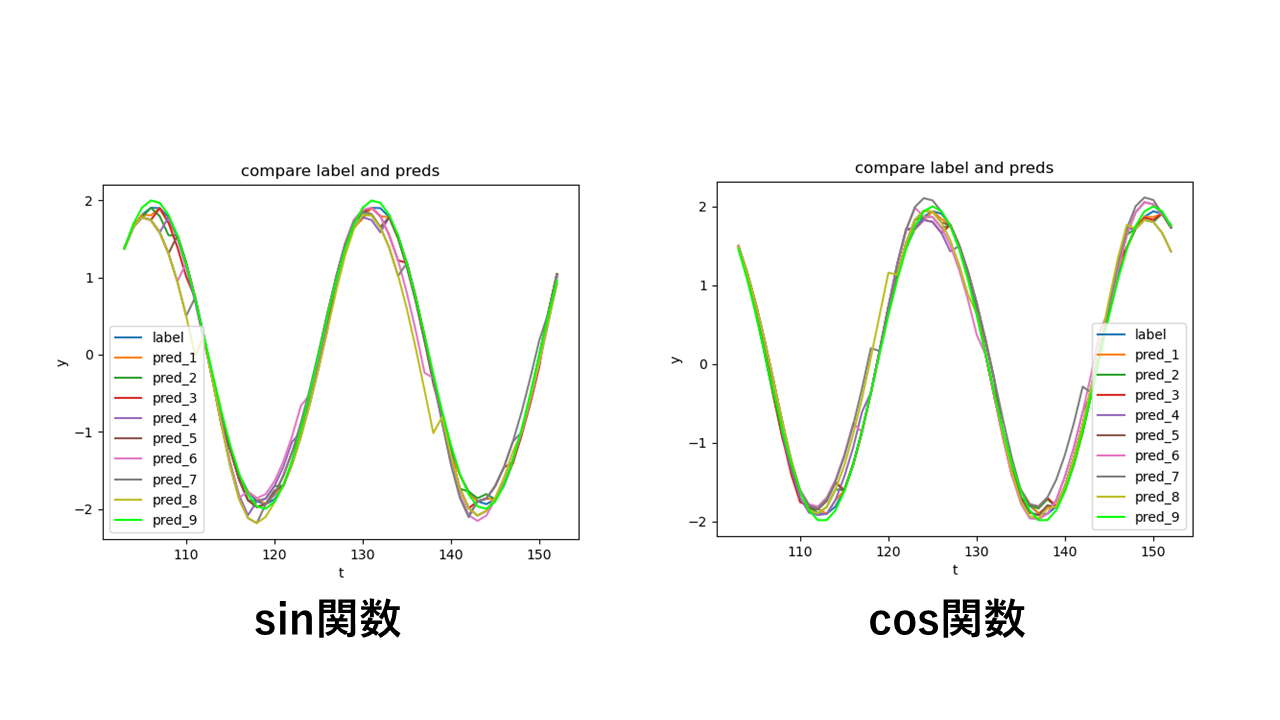
このプログラムを実行すると以下の図をプロットし,ターミナル上に予測した値から計算したRMSEの値を出力します.(calc_modeの変数でsin関数を予測するのかcos関数を予測するのか選択する必要があります)
図を見るとずれ大きく見えるものはいくつかあるが,振幅の2倍3倍ほど大きなずれはなく悪くない結果に見えます.
以下はsin関数の各予測した未来の幅ごとのRMSEと1つ先の未来を予測した時のRMSEを基準とした割合です.
RMSEの割合を見てみると,2つ先を予測した時点で+56.65479237021891%で,最大値は9つ予測した時の+578.8903915940437%でした.
また例外はあるものの割合は大体単調増加しています.
図を見ると悪くなさそうに見えますがRMSEの割合を見てみるとかなり悪そうに見えます.
数値で見ると人間の感覚では違いが良く判らないものも評価できるので良いです.
pred_step = 1, rmse = 0.0463193382933841, rmse_ratio = 0.0
pred_step = 2, rmse = 0.07256146323076017, rmse_ratio = 0.5665479237021891
pred_step = 3, rmse = 0.10495637762864339, rmse_ratio = 1.2659299872518808
pred_step = 4, rmse = 0.12224027240570762, rmse_ratio = 1.639076396805251
pred_step = 5, rmse = 0.16198444770642542, rmse_ratio = 2.4971235271200327
pred_step = 6, rmse = 0.13712321704460165, rmse_ratio = 1.9603880818864647
pred_step = 7, rmse = 0.22368511340234334, rmse_ratio = 3.829194924710157
pred_step = 8, rmse = 0.24009131197388198, rmse_ratio = 4.1833925271806995
pred_step = 9, rmse = 0.31445753712372515, rmse_ratio = 5.788903915940437
以下はcos関数の各予測した未来の幅ごとのRMSEと1つ先の未来を予測した時のRMSEを基準とした割合です.
sin関数の時と同様にRMSEの割合大体単調増加していて,割合のずれは大きく見えます.
pred_step = 1, rmse = 0.044212785920495934, rmse_ratio = 0.0
pred_step = 2, rmse = 0.06760037896588772, rmse_ratio = 0.5289780446644482
pred_step = 3, rmse = 0.0988830401746241, rmse_ratio = 1.2365258853499301
pred_step = 4, rmse = 0.13131762236247768, rmse_ratio = 1.9701277498915113
pred_step = 5, rmse = 0.1562937218522084, rmse_ratio = 2.535034461145652
pred_step = 6, rmse = 0.1124458296842421, rmse_ratio = 1.5432875884917954
pred_step = 7, rmse = 0.19061638995942234, rmse_ratio = 3.3113408483733977
pred_step = 8, rmse = 0.24447076357429492, rmse_ratio = 4.52941323385289
pred_step = 9, rmse = 0.2027480673314639, rmse_ratio = 3.585733812296931
6. おわりに
1つ先の未来を予測したときのRMSEの値を基準に考えると,精度良く予測できるのは+100%を超えていない2つ先までなのかなと思いました.
ただあくまでもこのプログラムの実験環境,パラメータの中でそうだというだけでもう少しパラメータをいじると結果は変わると思います.
理解が浅いところもあるので,いろいろ間違った理解や用語の使い方をしているかもしれないです.
遠慮なくご指摘頂けると幸いです.
またこの記事で説明したプログラムファイル(predict_simple_formula_train_m_to_m.py)やanacondaの環境ファイル(predict_simple_formula_env.yml)は以下のgithubにもあげているので良かったら見ていってください.
7. 参考にさせていただいたサイト