はじめに
今シーズンよりMLBのオリオールズに所属し,活躍が期待される菅野智之投手は,巨人時代に久保康生巡回投手コーチから,いわゆる「縦振り」中心の投球を強化する指導されたことより,2024年の活躍につながったと言われている.そして,今年も同様な指導で田中将大投手の活躍も期待されている.
縦振りとは一三塁方向(横方向)の回転軸とする投球の前後方向に動く回転を意味すると推測される.多くの人がもつ漠然とした縦振りのイメージは図1のようになるだろうか?
そして,それがもたらす投球への効果とはどのようなものだろうか?
ここでは,まずは身体の運動の回転軸を数理的に記述することを試み,回転軸の違いによる効果を明らかにする.この身体側の回転軸を可視化によって,投手の特徴とボールの回転への作用が見える.

図1:縦振りのイメージ?
ボールの運動から身体の回転軸を推定する
身体全体は多関節運動で,ボールの運動はその最終的な結果である.そのために身体各部位の運動の加算を行うのは面倒だ.そこで,全運動の加算結果はボールの運動に現れるため,ボールの運動から回転軸を計算するほうが手っ取り早くむしろ正確だ.ここでは,身体の回転を身体の運動を解析するのではなく,「ボールの運動から(ボールの運動に影響を与える)身体の回転軸を解析する」ことが狙いである.この記事では,さらにその身体全体の回転とボールの回転間の力学も考える.
なお,ここで強調したいことは,腕の角度や動きのような見た目の問題ではなく,ボールに対して所望の回転を与える身体の回転を力学的に考える.ボールの運動を変化させるのは,見かけの運動ではなくボールに作用する力である.恐らく良いコーチは,動きからよい力学を感じる能力があり,スキルを獲得するための多彩なドリルを持っているのだろう.

図2:多関節運動を一つの振り子運動で記述
ボールの回転軸と向心力
この記事で対象としている球種はストレートである.変化球となると少し事情が異なる部分もあるが,まずは自然な投げ方であるストレートを分析することで,身体とボールの回転の力学を考える.
なお,同じストレートでも投手によって「ボール」の回転軸は大きく異なる.回転軸の違いは握り方にも影響を受けるが,投げ方による影響が大きい.恐らく「握り方」と「投げ方」の両方のマッチングが重要だろう.
投球の力学メカニズム(1) -母指の離脱はバックスピンを誘発しない-で述べたように,ストレートの制御は転がりである.
つまり,ボールは転がっているが(回転しているが),力が作用する代表点(力の作用点)をボールの中心から眺めた外の方向(絶対座標系で見た方向)は,ボールの回転を制御している間(わずか20ms程度:ここで「ボール回転制御フェーズ」と呼ぶ.)は常にボールの外に向けて同じ方向を向き,回転制御フェーズ中の大半は同じ位置に留まる.図3の左の青色の大きめの点は,回転することで右のように移動するが,その間も力の作用点は同じ位置にある.
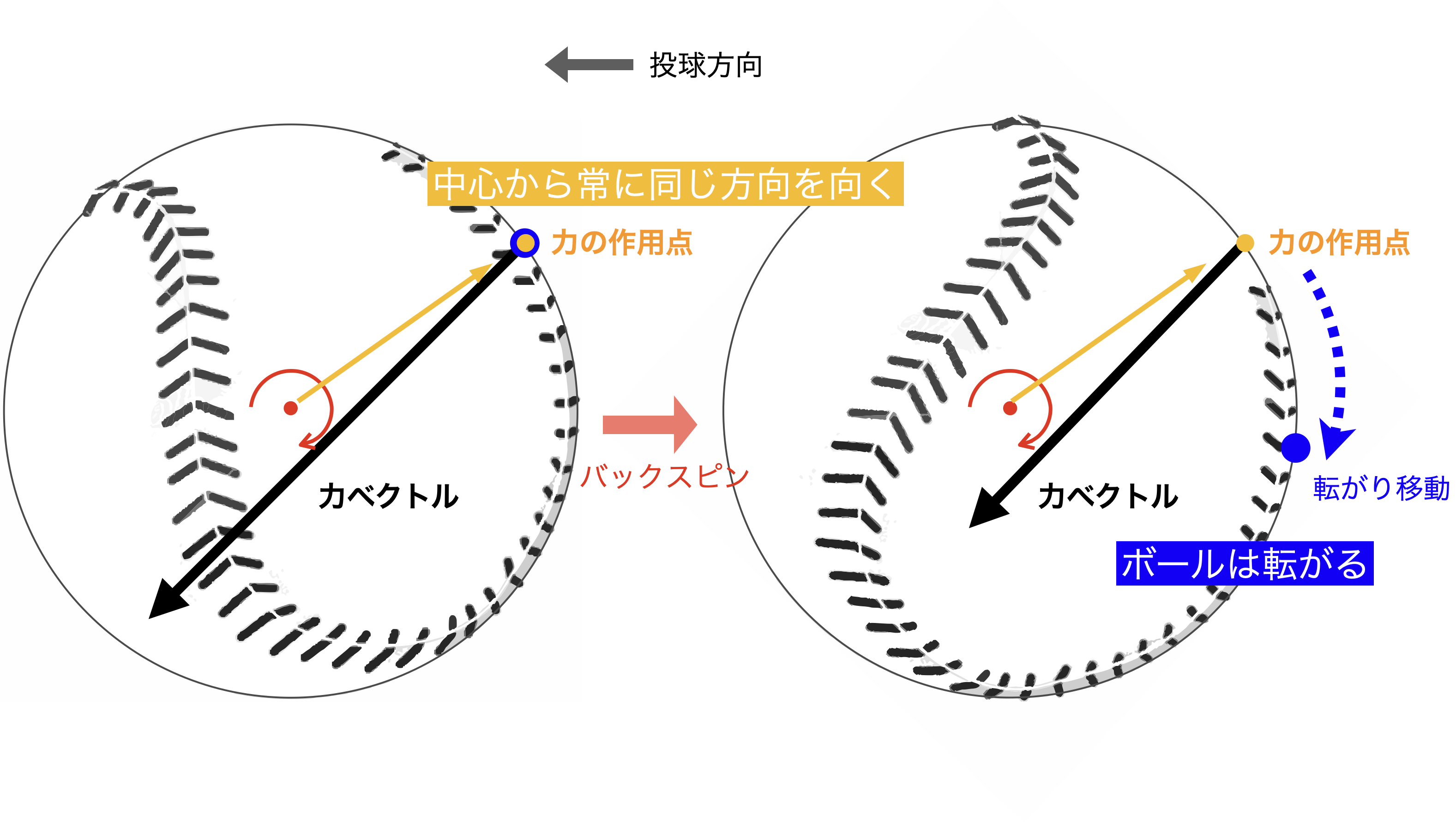
図3:回転制御フェーズ中に転がっている間でも,力の作用点は常に中心から同じ方向を向いている.
このように,同じ位置に力の作用点を留める(同じ位置に力が作用する)ことで,130~140km/hの投球においてこのリリース前のボール回転制御フェーズでは,20~30km/h程度速度が増加し,ボールの回転数(角速度の大きさ)の両方を増加させ,投球方向を定める重要なフェーズである.
また,この回転制御フェーズでボールに作用する力ベクトルの方向と,力の作用点の位置が,ボールの回転に影響を与える.しかし実際にはボールに与える力が,力の作用点の位置を強く拘束する.なぜなら,ボールに作用する力がボールの中心方向からそれることで異なる回転を引き起こすため,バックスピン以外の回転は起こってほしくないため,ヒトは自然に中心方向(詳細は後述)を押す制御を行うしかないというのが実態だろう.
バックスピン軸の定まり方
ここでは説明を簡単にするため,ストレートの投球で,おおよそ水平な軸まわりのバックスピンの投球を想定する.ただし,軸の方位(東西南北)の向きはどちらでもよい.
図4上はボールの真上から見たtop view,下の図は真後ろから見たback viewである.このとき,図3のように(side view),斜め下前方にボールを押していると状態を想像していただきたい.また左の(a)の場合,top & back viewで力はほぼボールの中心方向を向いているが,(b)では右側に力の作用点が位置する.
(b)のように中心からそれたやや右の位置に力の作用点が位置し,ボールを斜め前方にこのとき下向きの力は動揺にバックスピンの回転(赤)を引き起こすが,同時に他の軸の回転(青)も引き起こす.このような状態力の作用点が移動し転がりを実現できず,回転軸が一定とならないボールを不安定にさせるスピンが発生し,ボールに投球方向の力を与えることがすぐにできなくなるだろう.
つまりストレートのように転がりによってボールに回転を与え続ける場合,ボールの真上から見たTopViewや真後ろから見たBackViewで,おおよそボールの中心方向を向いている必要がある.さもないと,すぐに力を作用させられなくなる.バックスピンを与える時,横から見て力が下向きにそれることはよいが,残りのtop viewやback viewで,力ベクトルはおおよそ中心に向かう必要がある.
このことから,通常の投球ではtop viewとBackViewからみて,ボールに作用する力の方向と回転軸が「おおよそ」直交する方向を向く(ように投げるしかない).
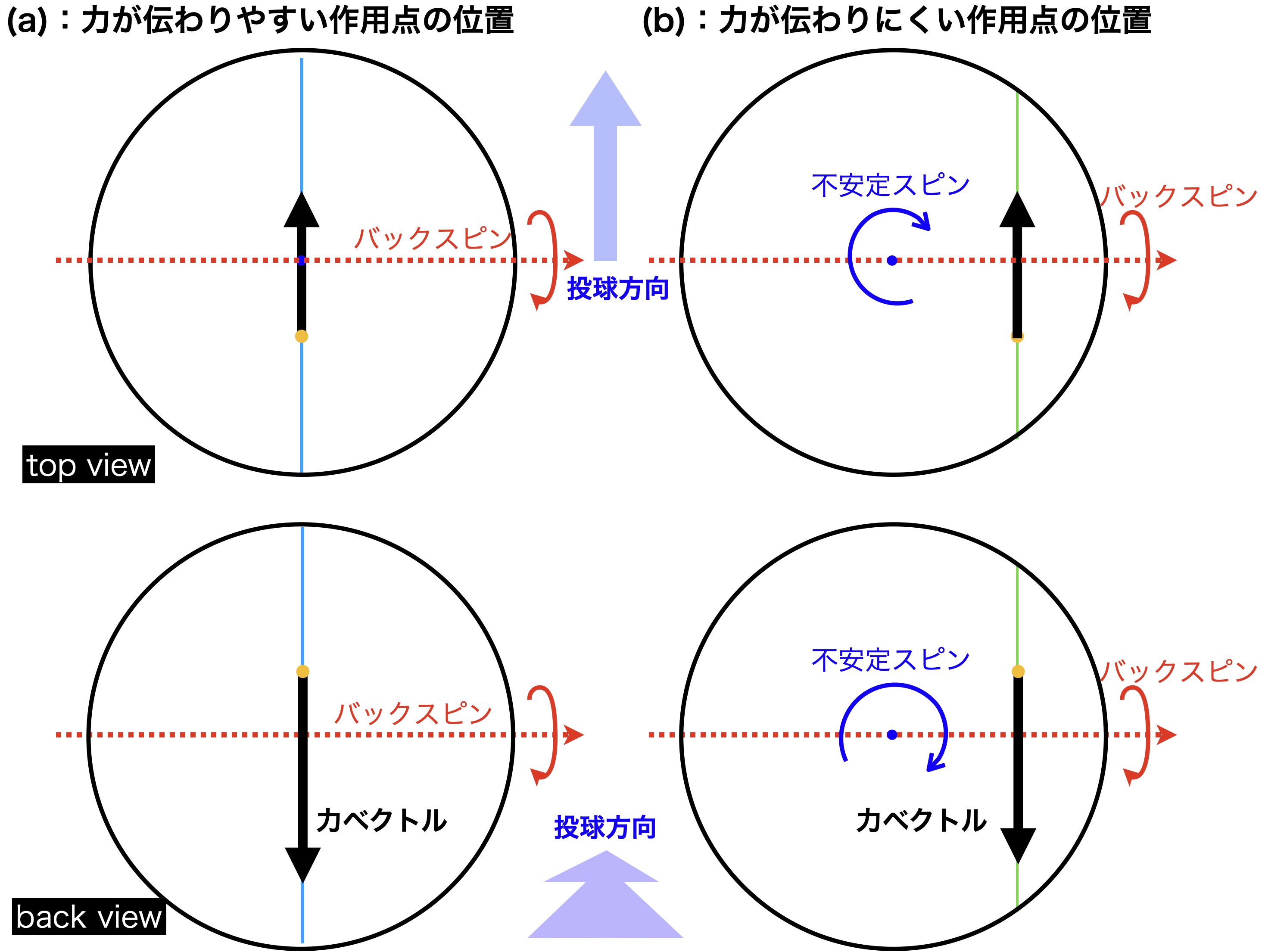
図4:top viewやback viewから見た時,(b)力が中心からそれることでバックスピン以外に
ジャイロスピンが発生し,ボールに力が伝わりにくい.
図5は,図4を斜め上後方から見た図である.
ボールに作用する力を水平軸と鉛直軸に分解し,その2つのベクトルで構成される(張られた)面が,ボール中心を大きくそれると不安定なスピンが発生する.

図5:図3の(a)(b)を斜め上方からみた図.ボールに作用する力(オレンジ)
それを水平方向の力と垂直方向の力に分解(黒)
また,図6のように,もしtop viewやback viewからみて力が斜め方向に作用すると,ボールのスピン軸も「おおよそ」図のように傾く(方位:東西南北の向きが変化する)ことになる.

図6: top viewやback viewから見た時,力の向きにおおよそ垂直な方向に回転軸が傾く.
図7で実際の投球データを見比べる.左右の異なる位置で投げているが,同じ座標系のデータである.少し見にくいが,y=0が,ホームプレートとピッチャープレートの中心を結ぶ線上に相当する.右の投球例はたまたまプレートの端の方に立って投げた例と考えれば良い.
左の投球例では回転軸(破線の軸:角速度ベクトルの軸)方向が,比較的真横(top viw)でかつ水平(back view)であることがわかる.これに対して右の投球例では,特に回転軸に前後方向成分が加わりtop viewで前後斜めに傾いている.このときボールに作用する力ベクトル(細い線.青いボールの位置にあるときの力ベクトルを代表して太く描画している)を,左右で比較すると,右の力ベクトルの左右($y$)成分が多く含まれ,回転軸がそれに直交するように斜めに傾いていることがわかる.また,back viewで比較しても,右の力ベクトルの$y$成分が多いことから,右下に回転軸が傾いている.
特にスピン開始の運動学的回転開始から,ボールに作用する力の向きが,ボールの回転軸に影響を与えていることがわかるだろう.これはスピンを開始する前(動力学的回転開始〜運動学的回転開始)はトップスピンの回転からボールの向きを大きく変えようとしているフェーズであるためである.
なお,必ずしも最適とか理想とまでは言えないが,揚力を生み出す上で効率の良い回転軸方向は,投球方向に向かって「真横」を向くのがよいスピンといえる.つまり,角速度ベクトル$\boldsymbol{\omega}=[\omega_x, \omega_y, \omega_z]^T$の$\omega_x= \omega_z=0$となる回転が効率よい回転軸えだる.そのような回転軸を生み出すためには,力ベクトル$\boldsymbol{f}=[f_x, f_y, f_z]$の$f_y=0$(力の左右成分を持たない力)が良い力の与え方と言える.つまり,図6のtop viewでは前後方向を向き,back viewでは真下を向くのがよいことになる.
実際には,図7で示したようにそのような方向に力が作用するとは限らないが,このボールの回転軸に影響を与えるボールに作用する力の向きは,どのようなことに影響を受けて変化する(傾く)のだろうか?

図7:回転制御フェーズ(動力学的回転開始:バックスピンのモーメント作用開始〜運動学的回転開始:
バックスピン開始〜リリース)におけるボールに作用する力(細い線)と,角速度ベクトル(破線)
角速度ベクトルはボールの回転軸を構成.上:真上から見たtop view.下:投球方向の後ろから見た
back view.時間間隔は1ms.
ボールのスピン回転軸は向心力の向きで定まる
少し復習する.
「投球の力学の基礎(1)-ボールに作用する力とボールの挙動:質点の力学-」で述べたように,ボールに作用する力ベクトルは互いに直交する「投球方向に作用する力」と,この紐の方向に作用する「向心力」とに分解できる(図8).向心力はボールの曲率中心方向を向いている.これは長さの変化する紐がボールにつながり,そのような振り子を回していると考えれば良く,その紐の方向は向心力が作用する方向である.ここで,このような仮想的な振り子を可変長振子と呼ぶが,その仮想的な紐に作用する張力を向心力と考えれば良い.この向心力が作用することには間違いないが,「ボールの回転運動を維持するための力」であって,運動中紐を切ってしまえば「投球方向にボールが飛ぶ」.
ここで図2を思い出しつつ,長さが変化する紐につながったボール(図8右)を想像していただきたい.曲率中心を原点とする特別な座標系でこのボールの運動を考えれば,ボールはひとつの回転運動で記述できる利点がある.つまり,ボールに作用する力を互いに直交する投球方向の力と向心力に分解できる.向心力は単に回転運動を維持するための力ではあるが,投球方向の力とともに黄色の矢印の力としてボールに作用し(図8),ボールの回転に影響する.なお,曲率半径(紐の長さ)が長いほど,ボールの運動が直線的になることを意味する.
そして身体全体の回転は,この紐とボールの運動(可変長振子)として考えることができる.曲率中心はボールに与える回転運動の中心である.つまり,縦振りなどを記述する際には,「ボールの曲率中心とボール間の直線」の運動として記述することで簡単に表現できる.

図8:ボールの運動の可変長振子モデル(長さを調節できる紐で回す運動)による表現.
投球の力と角速度を示した図7に,さらに曲率中心と可変長振子モデルの回転軸を図9に加筆した.この図は投手の後方から見たback viewである.向心力は曲率中心とボールを結ぶ直線上に作用し,投球方向の力はおおよそ前後方向に作用するので,真後ろからみると,総和のボールに作用する力(オレンジ)は,おおよそ向心力と同じ方向をむき同じ大きさとなる.
したがって図6(下:back view)で示したように,後方から見た曲率中心とボールを結ぶ線(可変長振子の軸)の傾きに応じて,ボールの回転軸も傾く.すなわち,回転軸を水平するためには,可変投振子の軸はボールから見て鉛直下方に近づく必要がある.
なお,図9の右の投球例のように,可変長振子の軸が大きく傾くほど,向心力の左右($y$)成分が大きくなる.
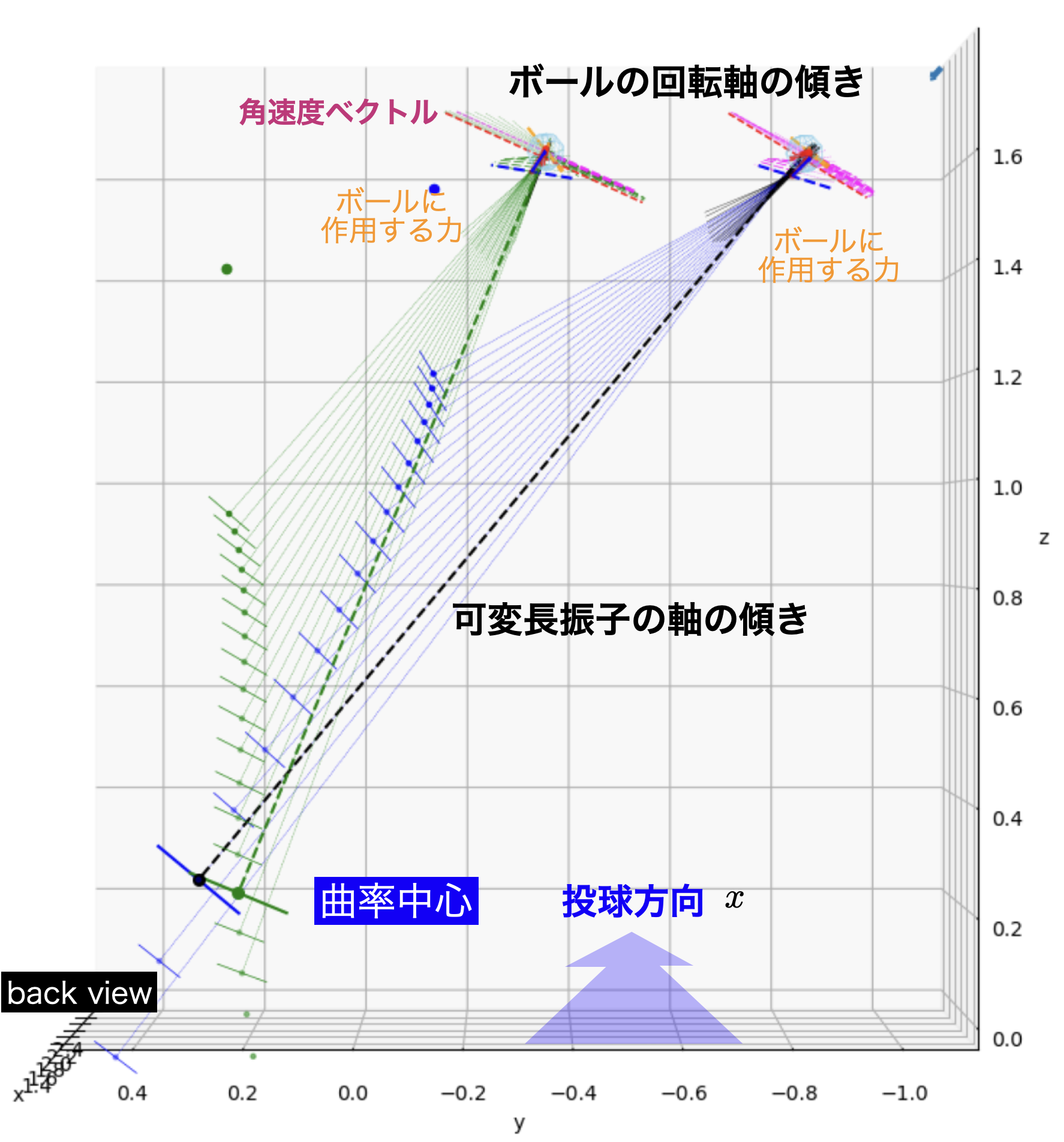
図9:後方から見た回転制御フェーズにおける,角速度ベクトルの傾き(破線)と可変長心の軸の傾き.
角速度ベクトルはボールの回転軸を構成.時間間隔は1ms.
図10は図9とおなじ投球を真上から見た図である.図中,力ベクトルの大きさが小さいのでわかりにくいが,右の投球では図7の可変長振子の傾きが大きいため,向心力の横($y$)成分が大きくなり,その影響でボールに作用する力(オレンジ色)が,前後方向から傾く.そして,この傾きが,図6上でも示したように,スピン回転軸が真横から前後方向への傾きを誘導する.
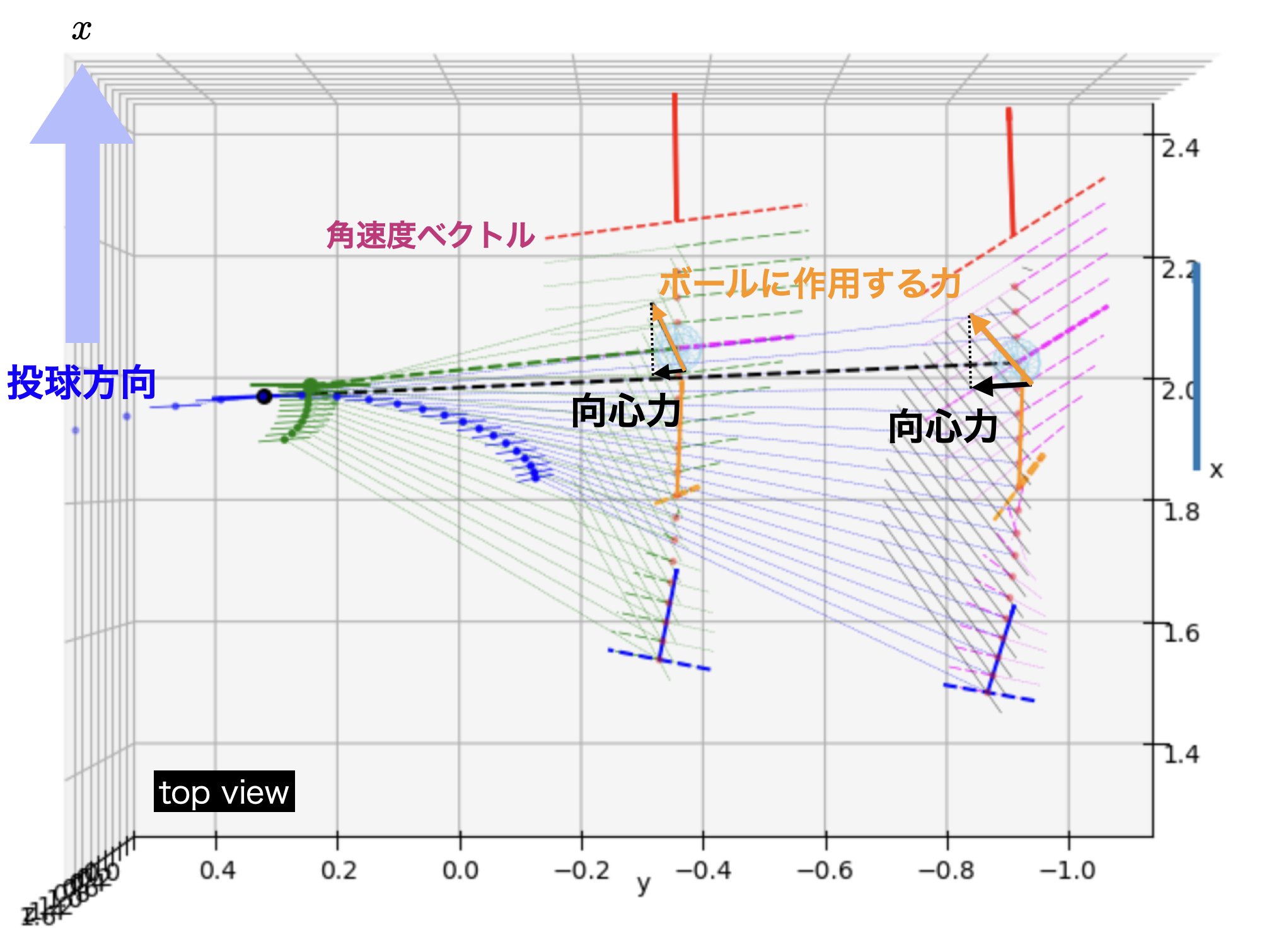
図10;真上からみた回転制御フェーズにおける,角速度ベクトルの傾き(破線)と可変長心の軸の傾き.
角速度ベクトルはボールの回転軸を構成.時間間隔は1ms.
これらの事実から,曲率中心がボールの真下から身体側(top viewの図9では左側の投球)に大きく移動することで,すなわち可変長振子の軸が斜めに傾き,そのことがボールのスピン回転軸の真横($\omega_x = \omega_z = 0$.理想?)からの傾きを誘導する.
もしボールの真下に曲率中心が存在するなら(向心力・紐の方向は上下方向),これがいわゆる力学的な身体側の「縦振り」に相当し,この縦振りがボールのスピン軸を真横に近づくように作用する.
なおボールのスピン軸が真横ということは,ボールの回転を効率よく揚力に作用させることを意味する.どれほど回転数が大きくても,回転軸が傾いてしまうことで,揚力などに効果的な回転成分を減少させることになる.
図7にボールの回転数を示したが,右の投球例では回転軸の傾きが少し大きく,揚力に貢献する角速度は$\omega_y=$1313 rpmまで減少する(角速度の大きさ$|\boldsymbol{\omega}|=$1722 rpm).左の例では$|\boldsymbol{\omega}|=$2019から$\omega_y=$1829rpmに減少するだけである.
したがって回転数の大きさだけでなく,ボールのスピン軸真横成分$\omega_y$が大きいこと(揚力を増加する実質的効果)や,スピン軸が真横(一三塁方向)を向くこと(回転数を最大限有効利用するという意味での効率)が重要だ.

図11:縦振りでは,ボールの真下近くに曲率中心が存在し,可変長振子の軸の傾きが少ない投球と考えられる.
図9,10では可変長振子の軸が傾くことで,向心力の水平成分が大きくなり,それが後方図におけるスピン軸の右下の傾き,真上図におけるスピン軸の前後への傾きを発生させることを示している.なお,厳密に,可変長振子の軸の傾き=スピン軸の傾きではな.あくまでも,そのような傾きを引き起こす回転力が作用するという意味である.
実際にそのような投球はできないと想像されるが,もし可変長振子の軸が水平になると,完全な横振りの投球になるが,実際には軸は斜めに傾いている.図8に示したが投手によってかなりこの傾きの違いは大きい.また,スイーパーの投球でお大きな効果を得るためには,軸は傾き横振りの割合が増えるかもしれない.
なお,サイドスローのような投げ方になるほど,横振りが大きいとは限らない.腕の傾きや運動方向ではなく,ボールに与える力が上下方向かどうかが重要だ.また,軸の傾きが必ずしも悪いとは限らない.
では,実際のどのような身体の使い方によって,縦振りの投球に近づけることができるかという問題は,前章の記事にヒントがある.肩はエネルギーの出入り口であり,同様に「腕を」可変長振子(長さの変わる振り子)として考えれば,腕回転運動の動力源は肩のトルクと,肩の加速度である.特に肩の加速度が身体全体で作られる加速度ということにも注意が必要だ.
縦振りとなるように,曲率中心が真下に近づけるようにボールに力を作用させるためには,腕の角度(arm slot)なども関与するが,ボールに下向きの力を発生させる身体全体の力発揮が重要で,サイドスローやスリークォーターでもある程度可能だろう.
最後に,可変長振子の後方から見た傾斜角度を図12に示した.同じぐらいの投球速度だが,かなりの角度差がわかる.この数値で,縦振り(完全な縦振りは90deg)の指標となる.
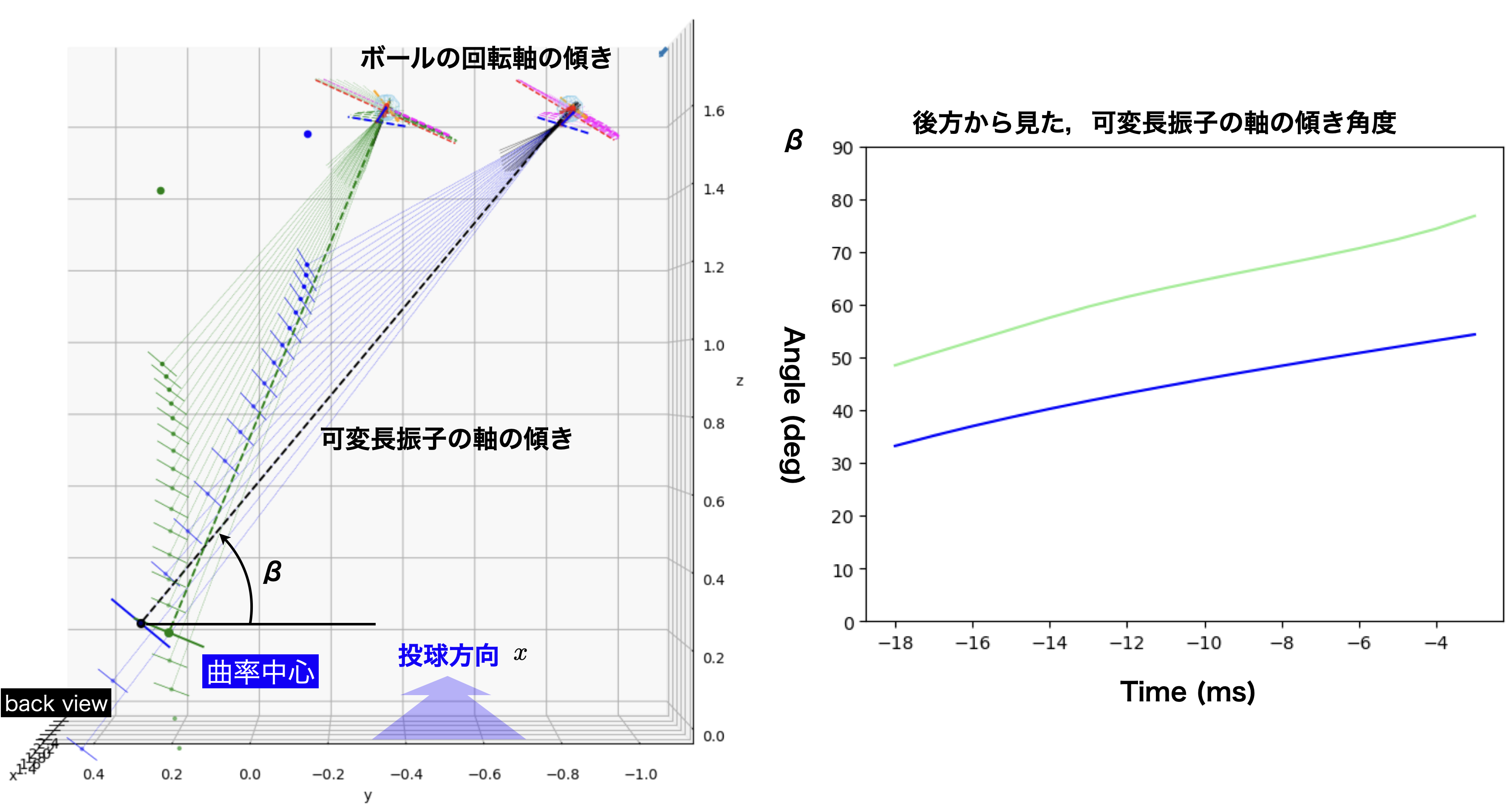
図12:図9の投球例における可変長振子の後方からみた傾き角度の推移(時間0がリリース)
リリース直前は曲率半径が大きくなり,かつ安定しないので除外している.
おわりに
恐らく多くの人がイメージする縦振りの正体は,見かけ上の回転の中心(曲率中心)をできるだけボールの真下方向に位置させ,ボールの真下方向に向心力を与えることだろう.腕を単に上に上げるだけでは,それを実現できず,前章でも述べたように,身体とボール間の押合いや引張り合いで作用する力を上下方向に近づけることを意味する.腰や体幹などの可動域は,必ずしもそのような上下の力を作用させるため適した方向に動くわけではないので,身体全体のねじれでエネルギーの漏れが発生しないような,下肢・体幹・上肢の使い方と強さが必要になるだろう.
もしここで述べた縦振りによって,ボールに作用する力の水平成分が小さくできれば,ボールの回転軸も投球方向に直交する水平軸(横方向)となり,効果的なボールのバックスピンを発生できるという効果が期待される.
前章の記事で述べたエネルギーの漏れが多くなり,ボールに力が伝わらなくなってしまった選手のトレーニングにおいて,「可変長振子の後方から見た傾斜角度」などは有効な指標となり得る.トレーニング前後で曲率中心とボールを結ぶ角度を比較することは有効かもしれない.