投球の力学の基礎(1) -ボールの力学挙動の概要：質点の力学-

はじめに

回転数や速度など，リリース後のボールの挙動はトラックマンやラプソードなどの計測機器で，簡単に投球直後に知ることができるようになった．問題はボールを「どのように制御するか？」であって，むしろリリース前のボールの力学が重要である．

このシリーズでは，投球におけるリリース前のボールの力学のメカニズムを明らかにし，たとえばストレートはなぜバックスピン回転となるのか？球種による回転のかけ方の違い，リリースのタイミングや制球などのメカニズムなどを明らかにする．

ここでは，それを理解するための力学の基本事項，特に，ストレートの投球における，リリース前のボールの並進と回転の力学的挙動の概要を述べる．

ボールに作用する力

図１：ボールに作用する力と，ボールの角速度（投手から見て左前方から見た図）（1kHzサンプリング）
　実際にファストボール（ストレート，約135km/h）を投球しているときの，ボールの軌道（赤点），
　ボールの回転軸（ピンクの破線，線の長さはボールの回転速度（角速度）の大きさを示す）を示す．

図１は，最大外旋位(MER)　と呼ばれる最も肩関節が外旋する（腕が最も後ろに引張られる）位置からリリース間の，ボールに作用する力ベクトル（オレンジ色）とボールの角速度ベクトル（回転軸）を描いている．これらは実際にモーションキャプチャで計測した投球データから計算された結果である（補足１）．またこれらは，1000Hzで計測されているので，1ms＝1/1000秒毎のデータが示されている．

回転（角速度）の表現方法については，補足２を参照されたい．

ボールが水色の位置にあるとき，ボールにはオレンジ色の力が作用し，この力は，投球方向（速度方向）に作用する力（赤）と向心力（青）の互いに直交する二つの力に分解できる．その二つの力の合力（オレンジ）が実際にボールに作用する力である．

図中の曲率中心などは後述する．

投球方向に作用する力：　ボールを加速する力（赤）

図１の「投球方向に作用する力」$\boldsymbol{f}_c$（赤）は，まさにボールの加速に寄与する力である．これは，ボールの速度（接線）方向に作用する力で，この矢印が長いほどボールはその瞬間それだけ加速する（補足３）．

向心力：　回転を維持するための力

向心力$\boldsymbol{f}_c$は，ボールが回転運動（円運動）しているときに，「回転運動を維持するための力」である．回転の中心（曲率中心$\text{C}$：補足４）に向かって，おおよそ曲率中心方向にボールを引張る力であり，遠心力（ボールが糸を介し，手に作用し，手を引張る力：$=-\boldsymbol{f}_c$）の反作用の力である（図２）．

ボールに紐をつけてくるくる回すことを想像してほしい．このとき糸に作用する張力（引張る力）のほとんどが向心力と考えて良い．張力には重力も含まれるが，向心力と比較すると無視できるほど小さい．なお，この糸で繋がれたボールは振り子とみなすことができ，長さ（曲率半径）が変化する振り子なので可変長振子と呼ばれる．

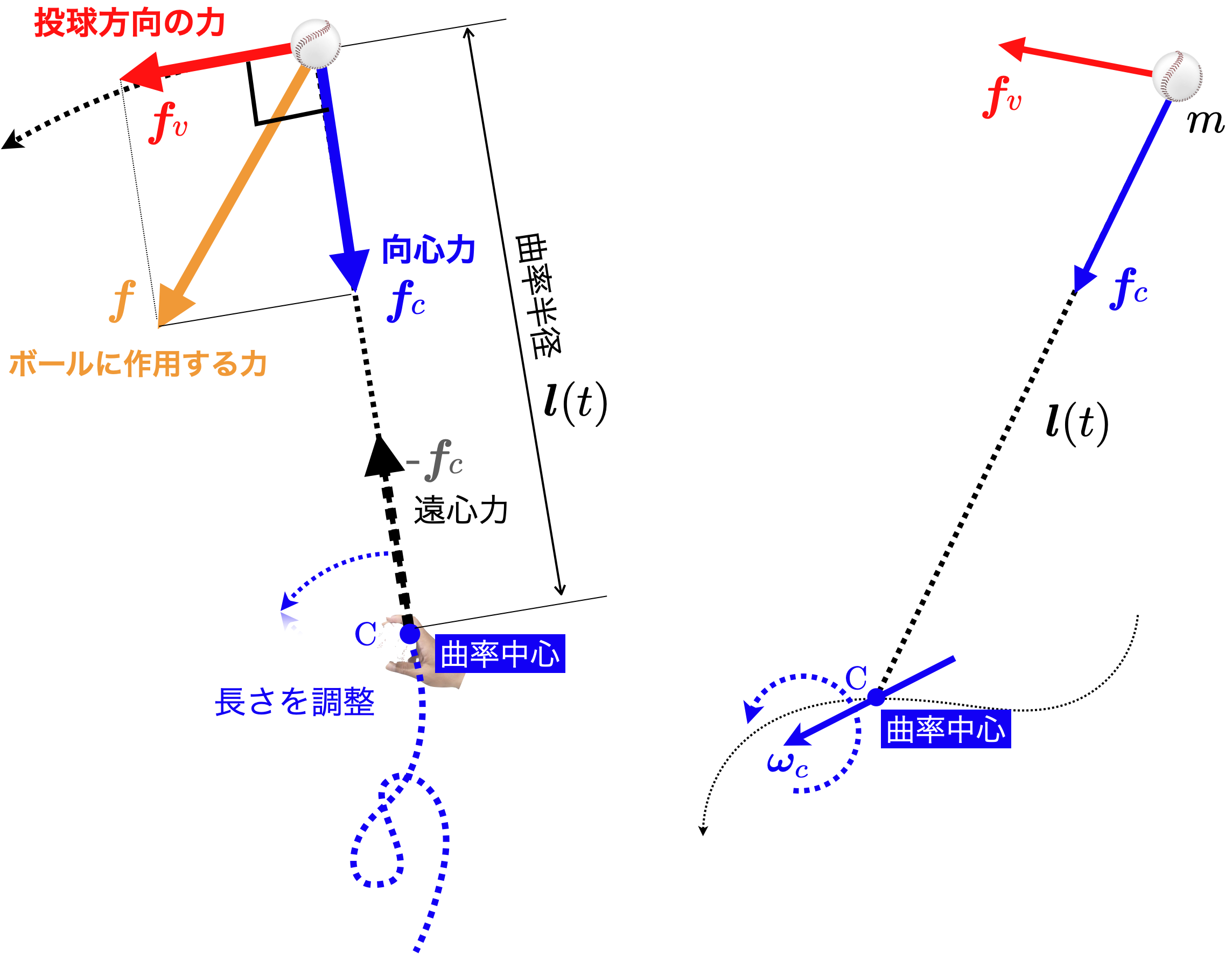
図２：糸でつないだボール(可変長振子）をぶんぶんまわす．

もし，その糸が切れたら，ボールは外側に逸れていくのではなく，あくまでも接線（投球）方向に飛んでいく．このことからも向心力は「回転運動を維持するための力」であることを認識していただきたい．曲率中心については補足４で述べるが，ボールの運動の回転中心と考えればよい．

向心力の大きさは，回転の中心（曲率中心）からボールまでの距離と，その中心から見た回転速度の二乗に比例する．

なお，「投球方向の力」と「向心力」の向きは直交している．

ここで，ボールには投球方向の力と向心力の両方が作用するので，合力として斜め下方向（おおよそ体幹に向かっていく方向．図１参照）に力が作用することに注意をされたい．

回転制御フェーズ

図３は図１を真上から眺めた図である．

図３：真上から見た図

ここで，バックスピンの開始を運動学的回転開始と呼ぶ．最大外旋位（MER）からこの運動学的回転開始までは，手全体でボールを握っていて，ボールは緩やかなトップスピンの状態で，ネジの向きは下向きである．したがって，MERからしばらくは緩やかなトップスピンのトルクが作用するが，途中でトップスピンのトルクが作用し始める．このトップスピンのトルクの作用開始を動力学的回転開始と呼ぶ．

バックスピン開始（運動学的回転開始）のとき，角速度は最小となり，その前後で回転軸の方向が変化するが，このタイミングで「母指がボールから離れ始める」．

図４の「動力学的回転開始」と書いている時点から，バックスピンを起こすトルクが作用し始め，実際にバックスピンの回転開始までには，この例では8msほど時間がかかっている．つまりこの間は，トップスピンの回転の勢いを，バックスピンのトルクで止めるフェーズである．

リリース後のボールの軌道や回転のは，動力学的開始からリリースまでのこの投球例では約20ms程度の間に定まる．この間を今後回転制御フェーズと呼ぶ．

おわりに

ここでは，質点とみなしたボールの運動を，曲率中心まわりの一つの回転運動で記述し，ボールに作用する力を，投球方向（接線方向）とそれに直交する並進力とに分解することで，ボールの力学的挙動を記述した．また，リリース前のボールの回転の挙動によって，フェーズ理由の定義を行った．このような運動の記述方法は，後ほどの章で活用される．

次回の記事「投球の力学の基礎(2)　-ボールに作用する力と力の作用線：剛体の回転の力学-」で，力の作用点について述べる．

ボールのダイナミクスの記述のために，ボールに作用する力とトルクがわかれば，剛体の運動を記述するうえで必要十分である．しかし，ボールの力学的挙動を理解するためには，力とトルクそのものでは，意味がわかりにく．そこで，曲率中心がわかればボールの運動の特徴が理解しやすい（？）ように，力の作用点を算出することで，ボールのダイナミクスがよく理解できる．たとえば，ストレートは転がりを活用して投げているなど．いったん転がりと理解できれば，それをどのように活用すれば，より良い投球の力学的戦略や，ノビという問題も見えてくる．

なお，この一連の記事で述べるボールの回転メカニズムは，バスケットボールや他の球技でも共通する重要な内容を含んでいる．それぞれに球技に合わせて考えていただければと思う．

補足

補足１

図A1のような８個ぐらい反射マーカを貼付し，剛体としてのボールの運動を計測している．
中心（重心）は非線形系の最小二乗法，ボールの姿勢は特異値分解を用いている．緻密な解析には，これらの精度が重要だが，さらなる改良を検討している．

図A1：ボール貼付した反射マーカ

補足２：角速度ベクトル

図１で回転軸を示したが，回転の速度（角速度）を表記する方法について説明する．図A2はネジの向きと回転の向きの関係を示す．

図A2：右ネジの方向と回転方向
　回転を表現する方法：矢印の方向を，右ネジが進む方向と考えれば，
 　右ネジの回転方向がボールの回転の向きを示す．

この線の長さが，角速度ベクトルの大きさを示している．ピンクの破線が長いほど，角速度は大きいことを示す．

補足３：投球方向に作用する力

ボールの位置ベクトルを$\boldsymbol{x}$とし，その加速度ベクトル$\ddot{\boldsymbol{x}}$を

$$
\boldsymbol{v} = \int \ddot{\boldsymbol{x}}dt + \boldsymbol{v}_0
$$
のように時間で積分すると速度ベクトル$\boldsymbol{v} = \dot{\boldsymbol{x}}$を計算できるが，ここでは少し変わった数値時間積分を行うことで，「投球方向に作用する力」の意味を理解する．

速度方向（接線方向とも呼ぶ）の加速度は

$$
\dot{\boldsymbol{x}}^T \ddot{\boldsymbol{x}}
$$

によって計算できる．この式の$\dot{\boldsymbol{x}}^T \ddot{\boldsymbol{x}}$は，速度ベクトル$\dot{\boldsymbol{x}}$と加速度ベクトル$\ddot{\boldsymbol{x}}$の内積で，つまりボールの加速度ベクトルのうち速度方向（接線方向）の成分だけを取り出している．つまり，「ボールを加速する力」とは，ボールの速度方向の力である．

そこで，これを積分すると，それはボールの接線方向の速度になることを示す．ので，ボールの加速度ベクトルを$\ddot{\boldsymbol{x}}$
とすると，その速度方向の成分の時間積分は
$$
a_i = \int \dot{\boldsymbol{x}}^T \ddot{\boldsymbol{x}} dt + v_0
$$
と書くことができる．これは，加速度の接線方向成分だけを抽出しているので，速度ベクトルではなく，速度だがスカラ（速度の大きさ）であることに注意されたい．これを実際に計算したのが，下記の図A3である．

図A3：投球方向の速度（青：速度ベクトルの大きさ，オレンジ：投球方向の加速度を積分 a_i）

青線は，単に速度の大きさ$|\dot{\boldsymbol{x}}|$を計算している．

ほぼ一致していることから，「投球方向に作用する力」$\dot{\boldsymbol{x}}^T\boldsymbol{f}$は，速度に寄与する成分という意味が理解できただろう．

残りの向心力成分は，回転を維持するための力で，ボールに作用する力は，この互いに直交する，「投球方向に作用する力」と「向心力」に分解できることがわかる．

補足４：曲率中心

ボールの運動を一つの回転運動だけで記述したいとき，曲率中心まわりの「ひとつの」回転運動だけでボールの運動を記述することができる．ただし，等速円運動をしていないかぎり，その中心は時々刻々移動する．

このときボールと曲率中心の距離を，曲率半径と呼ぶ（図A4参照）．道路標識でよく見かけるRのことである．Rが大きいほど半径が大きいのでそれは緩やかなカーブで，Rが小さいほど半径が短いのできついカーブとなる．直線運動をしているときは，半径は無限大となる．

図A4：曲率中心Cと曲率半径R

投球では半径は，時間経過とともに徐々に長くなる傾向にある（図A5）．肘関節を多少屈曲ぎみに，上腕の内旋運動のトルクを利用している投げ方の場合，曲率中心はよりボールの下に位置していく．

投球におけるボールの曲率中心の位置は，どこを中心にボールを回転しているかを示している．必ず，身体が形成する空間内になるとは限らないが，どこを中心にしてボールを回転させているかを示している．

すでに述べたが，投球方向に作用す力は，その半径方向と直交する方向である（図１参照）．

このように曲率中心を使って，ボールに作用する力を接線方向（投球方向）の力と，向心力に分解すれば，投球方向に加速する力と，回転を維持するための力に分解することができ，その意味がわかりやすくなる．

なお，曲率中心を計算しなくても，ニュートンの法則からボールに作用する力を，ボールの重心の二階微分と，重力加速度を考慮すればボールに作用する力が計算でき，そこから接線方向の力を引き算すれば，向心力は計算できる．

ただし，曲率中心の位置は物理的に特別な意味を持ち，その変化を観察することで，図1や図A3のように，その投球の特徴を示すことができる．選手間ではかなりその変化パターンは異なり特徴を示すし，選手の個人内でも調子の善し悪しの微妙な変化を観察することができる．３次元で投球の微妙な特徴を可視化するには非常に優れた方法である．お試しあれ．

図A5：投球中のボールの曲率中心の変化例
　最大外旋位近くではボールの曲率中心（回転の中心）は肩付近にあるが，次第に遠くなり回転の中心は
　左下の床近くまで伸びていく．基本的には右投手の場合，右肩から体幹付近の下に位置していく．
　球種でも全く異なるので，球種による違いをさとられない投球の練習にも使える情報だ．
 力強い投球をする場合は，リリース近くまで半径が短めで，急激に曲率半径が伸びていく．

剛体の運動の意味を知りたい場合は，瞬間回転軸を描くとよいだろう．

曲率中心の数学的な詳細は，note記事「Sports Biomechanics Geek #7　〜多関節運動の代表値　曲率の力学〜」も参照されたい．

補足５：ここでのアプローチ方法

「はじめに」でも述べたが，バイオメカニクスの分野で統計的な分析が多い．しかし，それは「たまたまそう見えているだけ」ということもある．複雑な解析を利用することもあるだろう，しかし，そこで力学は使って分析を行っていても，結局，量と量との関係性を述べる統計の世界だ．特徴がわかることはとても重要だ．しかし，それがボールの挙動を定めている「理（ことわり）」を理解することにつながらないケースも多い．

神経科学は，脳の中で何を行っているかをうかがい知るために，統計や量的な解析に頼るしかないだろう．しかし，身体運動は力学法則が厳密に成り立っている．理論的なアプローチが可能なのだから，分析だけではなく，もっと数理を活用することが懸命だ．ここではそのようなアプローチを示すことで，皆様のお役に立てるように努めたい．

なお，過去に書いた記事は，少し専門的であったので，ここでは，できるだけわかりやすく述べていきたいが，どうしても数理について述べるので，数学の力で説明することがあるかもしれない．その際はご容赦いただきたい．

数学的・物理的必然性

ここでは，基本的には精密な計測・解析データに基づき，単なるそれらの統計や物理量と物理量の関係だけから述べるのではなく，可能な限り数学的必然性（ロボティクスの杉原知道先生の言葉 1）に基づいたメカニズムについて述べていきたい．

ボールは自由に制御できるわけではない．スピンをかけたいから，下向きに簡単に力を作用できるわけではない．ボールから指を離せば回転し始めたり，リリースするわけではない．幾何学的・解剖学的な拘束や，力学拘束や幾何学拘束にかなり束縛されながら運動を行っている．たとえば球速を増加させようとすると，制球力が衰えるなど，ことは簡単でない．ただし，そのような理を理解せずとも，ヒトはその自由のなさ（束縛）を反対に活用しながら，あっさりと投球を行っている．下手ではあっても多くの人はボールを投げることは可能だ．しかし，ロボットにそれを実現させようとすると，それなりに大変だ．投球と呼べるような運動を数理的に理解し実現するのは，なかなか難しい課題である．

このような何か（たとえば速度）を増やそうとすると，何か（たとえば正確性）が劣るようになってしまうという構造（拘束）は，身体運動にとっては矛盾を引き起こす．そのバランスを取りながら，両方とも解決することが身体運動で求めらる．

そして，このような束縛は多くの場合，身体の「末端」や，末端での「道具と身体間」で拘束することが多い．そのような拘束を守らなければ運動がそもそも成立しない．したがって，その力学拘束を「身体全体に分配」する強い拘束が支配する．バイオメカニクスでは末端への伝達という逆方向の視点が中心で，その視点が欠けてしまうことが多い．

そのような理解は，単に投球や野球の理解だけにとどまらず，きっと他の運動の理解にも役立つことだろう．「理（ことわり）」に基づいてれば，どこまで言えるか，それが当てはまるか，理論的な正しさの範囲も教えてくれる．また，そのような理解はロボットなどの強化学習や機械学習では実現できないような運動の実現にも役立つだろう．

また，スポーツのような運動は身体運動の特徴を「顕在化」する．スポーツのような運動は，日常行うような運動ではないが，身体からするとスポーツは特別な制御を必要とする運動ではない．スポーツをするときに脳の回路が入れ替わったり，神経系が特別な制御を行うわけではない．あくまでも日常の身体運動の延長である．スポーツのような運動を通して，我々が行う運動のメカニズムを顕在化させることは，身体運動の理解のために，それはとても良い題材となる．

参考文献

1.　杉原知道，ロボット工学に基づく二足歩行制御の構成論的理解（第75回 ロボット工学セミナー 歩行の生理学／力学／制御理論と歩行支援ロボティクス），2012

2.　太田，福田，那須，木村,力の作用点による投球の回転制御の解析, 第45回バイオメカニズム学術講演会（SOBIM2024）2024.12