はじめに

記事「投球の力学メカニズム(2) −バックスピンは運動連鎖−」で,運動連鎖という観点からストレートの力学のメカニズムについて述べた.ここでは,その記事の内容を補足しながら,投球の力学を通し「ヒトらしい運動とは何か?」という身体運動の物理的意味を考える.
これは投球を通しての身体運動のメカニズムについての考察であるが,この問いに対する答えから,すぐに良い投げた方などの直接的な答えを導くことは難しいかもしれない.しかし,統計や経験などの局所的な理解に基づく指導の誤りなどを防ぎ,身体運動全体に当てはまる普遍的な理解を数理的に記述することで,将来的には新しい投げ方の提案や自動的な身体運動の生成技術などを可能とするだろう.
投球における運動の自然さ
運動パターン形成
投動作は日常生活では投げる動作を行う機会は少なく少し特殊な運動ともいえるが,他の動物は行わないという意味でヒト特有の運動である.
学習の程度によって巧みさや速度などの違いはあれど,プロ野球の投手の動作と単に物を投げる動作は同じ投げるという運動パターンに落ち着く.このことからヒトは物を投げる動作という共通の運動パターンを生成する理由があり,投動作はヒトらしい自然な運動のひとつである.そして野球の投手のように「投げる」動作の学習を極めることで,より「ヒトらしさ」や「自然さ」が顕在化する.
スポーツという特殊な運動を通して,身体運動における普遍的なヒトらしさを考えることは,適切な方法ではないと思えるかもしれない.しかし日常における身体運動においても,極限に近い結果を求めるスポーツのような運動でも,同じヒトが運動を行っている以上,制御原理が突然大きく変わるわけではない.変化しているのは運動の目的や拘束条件だ.スポーツの運動はヒトの運動の特徴をむしろ顕在化するため,ヒトの運動の制御原理を理解する上でむしろ都合が良い.野球に限らずその競技の特殊性を,身体運動(または生物の運動)の普遍性から俯瞰すれば,それを特殊性ではなくバリエーションと捉えることができる.ここでは投球動作の特殊と思われる特徴も,単に目的や境界条件によって変容したバリエーションにすぎないという立場だ.
動力伝達による運動パターン形成
この記事で述べていきたいことは,運動の目的(投球ならボールを正確に速く投げること)と,動力の伝達の仕方が,投げる運動パターンを形成するとということである.動力伝達が運動パターン形成の最も強く拘束することは,投球に限らず他の運動でも同様である.
ここでは,動力伝達は,身体間のエネルギーの伝達や移動に相当し,動力として,力ベクトルと速度ベクトルの内積で記述される仕事率(パワー)を考える.これは,単位時間あたりにどの程度エネルギーが変化するか(エネルギーの時間変化率)を意味する.
運動における自然さとは?

図2:バックスピンも自然な運動
野球の投球においてストレートは多くの球種の中で,最も自然な投げ方をする球種である.何も考えずにボールを投げれば通常バックスピン(図2.補足1)のストレートになるということもあるが,この自然さとは野球に限らずヒトの運動における自然さである.それはこれまで述べてきたようにヒトらしさとも言える.
「ヒトらしさ」「自然さ」とは曖昧な表現だが,同じルールで形成された運動パターンには大きなバリエーションがあり,下手くそな人や子どもが投げる動作も,プロ野球の選手が投げる投動作も同じ運動パターンとしてやんわりと分類され,曖昧な「自然さ」「ヒトらしさ」という表現を用いる.ただし,関節の速度などの見た目(出力)だけで(運動学的に),それがヒトらしい運動と厳密に判断することは難しいかもしれない.
では,ヒトらしい運動パターンを形成するルールはどのようなメカニズムに基づくのだろう?
関節に作用する力による動力伝達
そもそも投げる動作は日常ではあまり行わない運動で,どちらかというとスポーツ特有の運動であるが,まず投げる動作がなぜ「ヒトらしい自然な動作」か考える..
動力伝達は身体の各部位間の「エネルギー伝達(流れ)」と考えても良い(補足2).たとえば,図3の部位A,B間の関節には作用反作用の力$\boldsymbol{f}$と$-\boldsymbol{f}$が作用する.この作用反作用の力が部位A,B間のエネルギーの移動,すなわちエネルギーの流動を引き起こす.ここにおける作用反作用の力は力学では内力に相当する(補足3).
なお,動力伝達の媒体となるのは並進の力であって,関節に作用するトルク(回転力)ではないことに留意されたい.また,このことは力学的な要因が自然でヒトらしい運動を形成していることを意味する.ここでは深く述べないが,恐らく身体運動の特徴として取り上げられる「滑らかな運動」も,制御や神経科学的な都合ではなく力学的な理由から発生する現象だろう.

図3:関節に作用する力とトルクと動力伝達
肩はエネルギーの流出入口
手首などの末端の関節の筋力が発生するトルク(回転力)は極めて小さく,投球のような「高速な運動」では,速い球を投げるために手首の関節力(トルク)だけでボールに十分な力を与えることができないため,他の部位からの動力の供給が必要となる.また,大きな動力源は末端から離れた下肢や体幹など部位にあることも理由となる.なお,動力源は一箇所に存在するわけではなく,「動力は下肢・体幹などの複数の部位で協調しながら生成される」(図4).投球(投擲も)では,肩から腕側は振り子,体幹と下肢は動力を生成する部分と明確に分けられ,肩はエネルギー流出入の出入口である.

図4:体幹と下肢による動力生成.動力は身体各部位の全体の押し合いによって発生する.
他の運動における動力伝達の例
関節に作用する力の媒介によって実現する動力伝達がヒトの運動パターン形成を担っていることは,日常の身体運動を観察していては気が付かないかもしれない.
ハンマー投の運動をモーションキャプチャで計測すると,それがパラメータ励振のように振動的で,ハンマーと手間の作用反作用の力によってエネルギーが腕とハンマー間で行ったり来たりしながら伝達されている.ハンマーと腕間の作用反作用の力(=ワイヤーの張力)以外にハンマーへのエネルギーの伝達方法はない.ハンマーの力学的エネルギーは増減を繰り返すが平均的には増加する.ターン運動を行ってハンマーを加速している間,腕とハンマーはほぼ真っすぐに伸び,わずかに最大でも20deg程度変化するだけで,正確に計測を行わないと腕とハンマーの関係が振動であることはわからないだろう(文献1,2).
ゴルフスイングでは,スイング中に手とクラブ間にトルクも作用するが,それでも手とクラブ間に作用する力がエネルギー伝達の中心を担う.そして,運動によって質量などの違いから振幅などに大きな違いがあれど,どちらの運動もスイング運動を行い,関節に作用する力が運動パターンを形成している(文献3)(補足4).
この原理は,歩行や走行でも,キック動作にも当てはまる(文献4).
動画(名古屋工業大学,佐野研究室)のロボットの歩行(左)では,膝関節も含めてどの関節にもモータ(アクチュエータ)は存在しない.単に僅かに傾いた斜面を下っているだけである.このような歩行は受動歩行と呼ばれ,わずかな重力以外の動力供給はないが,右のヒトの歩行と同じような運動パターンを生成する.つまり関節に作用する力が動力伝達を担い,自然な運動パターンを形成していることを示している.制御を全く行っていないにもかかわらず,モータのない機構だけでまるで歩行のような運動を効率よく実現できることは驚くべく事実である.
これらの例からも,ハンマー投のようにこれらの運動は見かけ上異なると感じるかもしれないが,日常行う歩行運動を含めたスイング(振り子)運動という運動パターンは,関節に作用する作用反作用の力を媒介した末端への動力伝達で形成されることを示している.一方,投球における肩関節のトルクも,ゴルフスイングにおける手関節のトルクもスイング運動に貢献するが,スイング運動の運動パターン自体は,関節間に作用する力(バイオメカニクスでは,関節間力などと呼ばれることもある)による動力伝達に由来すると考えるのが妥当だ.
振り子(テコ)による動力伝達
スポーツに限らず,手先などの末端(end-effector:手先効果器)に作用する負荷が大きくなれば,その動力を離れた部位から獲得する必要がある.このとき動力の伝達を担う中心は,やはり関節に作用する力(作用反作用の力)である.これは骨と骨が押し合う力であって筋力や回転力(トルク)ではない.歩行や走行も動力を関節に作用する力を通じて体幹や下肢から足に伝達している.動力伝達は動力の分配と言い換えることもできる.
もし(手先などに)作用する負荷が小さく,比較的ゆっくり運動する場合には,他の部位からの動力伝達は必要なくなり,ローカルにまかなうことができる.指先を動かす程度あれば,腕を動かすまでもなく,指の関節や手関節だけを動かせば良い.しかし,日常生活でも少し手先の出力が大きくなると他の部位からの動力伝達は必要となる.
さらにスポーツのような高速な運動が求められ場合は,振り子(テコ)が用いられる.二重振り子の運動のメカニズムを考えると良い.振り子間の関節にモーターなどのアクチュエータがない機構で,先端の振り子に動力を伝達するためには,関節間に作用する並進の力(作用反作用の力)で伝達する以外に方法はなく,二重振り子では関節に作用する力が唯一の動力を伝達する手段となる.
二重振り子の動画みていただきたい.振り子間の関節にアクチュエータ(筋肉)がなくても,先端の振り子に動力を伝達し,先端の振り子を回すことができる.これは,関節間に作用する作用・反作用の力(バイオメカニクスでは,関節間力などと呼ばれる)が,動力を伝達していることを示している.根元側の振り子の運動の振幅や速度は小さいが,振り子は高速に回転していることにも注目されたい.なおゴルフスイングやハンマー投では,身体の腕が根元側の振り子,クラブやハンマーが先端側の振り子と考えれば良い.投球では体幹と下肢全体が根本側の振り子で,腕が先端側の振り子と考えれば良い.
根元の筋肉の動き(収縮速度)自体はさほど速くない.そこで,動力(力$\times$速度)を伝達する際に,力と速度の割合を梃子(テコ)が変換する.振り子も根元側の動きの振幅は小さく速度も小さいが,先端は高速な運動に変換される.
図6に示すように1:2の梃子は,根元で力1を与え速度1で動かすと,先端では力を2分の1に,速度を2倍に変換する.梃子は動力(力と速度の積)を一定に保ったまま力と速度の割合を変換するツールで,身体運動では腕や脚などがその役割を果たしている.

図6:梃子の力・速度変換.1:2の梃子は,力を2分の1に変換し,速度を2倍に変換する.
ただし,動力(力と速度の積)は一定である.
いずれにせよ,動力伝達の中心は「関節に作用する力」を媒介したエネルギーの伝達であることを示している.
この振り子運動は,投球に限らず,多くのスポーツでスイング運動(「ムチ運動」などとも呼ばれることもある)として観察される.運動連鎖とも呼ばれる.
ただし,投球時の肩から下の部位から発生する動力が,すべてボールに伝わるわけではない.伝達のメカニズムを考えると致し方ないのだが,振り子運動ではかなりの動力の伝達ロスが発生する.振り子運動で高速な運動に変換する際,どうしてもエネルギーは腕の運動エネルギーとして消散してしまう.そして遅延も発生する.これは避けられない.力レベルでは,たとえば地面反力の最大値が約2000Nとしても,ボールに作用する力最大値は200N以下にしかならない.速度に変換されるので,力ほどではないがエネルギーもかなり減少する.速度が大きくなれば末端では伝達効率は極めて悪い.
二重振り子による動力伝達と回転運動への変換
動画に示したように,ヒトは容易に二重振り子運動を操ることができるが,適当に動かしては制御することはできない.振り子を構成する梃子は,根元の小さな運動を先端で高速な運動に変換するツールとして有効であることを述べたが,ここでは関節に作用する力を,振り子の回転運動にどのように変換しているか概略を述べる.
なお,以下の議論は二重振り子の回転運動の加速中,根元と先端の振り子は両方で遠心力と向心力で引っ張り合いを行っている状況であることに注意されたい.
図7の左側に示したが,先端の振り子Aを左側に回転させる際,振り子Aの根元側にある関節部分に対して反対側に加速度をもたせることで,振り子Aは回転する.この根元部分の反対側の加速度は,実は図7右の下の振り子Bの向心力によってもたらされる.わかりやすく述べると,上の振り子Aの遠心力と,下の振り子Bの遠心力(正確には上の振り子に対して向心力として作用する)の引張り合いで,上下の振り子がまっすぐになろうとする性質が振り子の回転運動に大きな役割を果たしている.
したがって,この引張り合いは上下の振り子のなす角度$\theta$(図7左参照)に応じても変化し,$\theta$が90度に近いほど下の振り子から作用する向心力を有効利用できる.
これ以外の力(たとえば,向心力に対して直交する方向に作用する振り子Aの角加速度)も,振り子Bの回転運動に寄与するが,この遠心力と向心力の引っ張り合いが支配的であることを覚えていただきたい.このことは,後半の「自然な回転」や補足6で再度,詳しく述べる.

図7:二重振り子の力学的な加速メカニズム
動力生成
動力は地面から湧き出るわけではない
最近,ゴルフや野球でも地面反力の重要性が認識され,地面反力の伝達の重要性が選手レベルでも語られるようになってきた.このことは間違いではないが,動力は地面から末端へ一方通行で伝達されるわけではない.ボールに作用する力は力学問題を計算するうえで「見かけ上」,地面から下肢・体幹・腕と順次計算をして解いていく.この解き方が,地面から動力が湧き出てくると勘違いさせるのかもしれない.地面以外に相互作用がない限り,身体全体からみると地面反力は重力以外の唯一の外力であるが,地面に筋肉やモータなどのアクチュエータがあるわけでなない.
大きな動力は,地面と身体全体の押合いで発生する.地面反力はいわば身体全体の「おしくらまんじゅう」による成果である.動力を生成する部位では,押合いによる「動力生成と伝達を同時に行う」.なお,動力生成は複数の部位の協調によって生成するが,やはり動力の生成と伝達を担うのは関節に作用する力である.

図8:地面反力は身体の押合いの結果.力学的には身体各部位の加速度と重力加速度の総和である.
関節を動かさないようにすることで動力が生成される
関節に作用するトルク(筋力)は,動力生成と動力の伝達の両方に貢献するが,力は発揮しつつ,どちらの目的のためにもできるだけ「関節を動かさない」ことで,動力生成と動力伝達を促進する.エネルギーを逃がさない(漏らさない)目的でも,関節をできるだけ固定することが重要で,見かけ上トルク(筋力)は,関節に作用する力による伝達をアシストする役割を果たす.関節を動かしているのにもかかわらず動かさないようにするということは,アイソメトリックな運動に近づけると言い換えることができるだろう.身体全体を多くの油圧ポンプで押しながら強力なエネルギーを発生していると思えば(おしくらまんじゅうでも良い),1箇所でも弱いところがあればエネルギーはそこから漏れ出してしまう.
なお,このことを運動方程式で考えるならば,ニュートンの運動方程式が動力伝達の支配方程式となり,オイラーの運動方程式は動力伝達のアシストや漏れを記述することになる.
なお,アクチュエータである各筋肉が身体運動の動力源であることは間違いない.ここでの議論は筋力によって発生する(関節に作用する)トルクと関節に作用する力を,ひとつひとつの関節レベルやローカルに現象を観察するのではなく,身体全体での役割について議論していることに留意されたい.

図9:関節を動かさないようにすることで動力が効率よく生成され伝達する.
運動連鎖
バイオメカニクスでは,「下肢や体幹側の運動」と「腕側の運動」のメカニズムを区別せず,どちらも同じ運動連鎖としている.投球においても地面から運動の連鎖などで逐次動力を伝達していると考えがちだが,肩から下の部位では振り子運動は起こっていない.そもそも振り子運動はエネルギー伝達効率が悪い.体幹は細長い構造でもないので振り子運動に適さない.スイング運動は高速な運動に変換するために必要な運動で,伝達のために振り子間のなす角度(位相差)が必要だ.しかし,肩から下は腕と地面との押し合いによる動力生成部位である.
動力を生成するために,弓のように身体を反ることは必要だが,その部位間の角度差が末端の振り子運動を連想させるのかもしれないが,逐次運動(量?)が伝達すると考えるのはやめたほうがよい.多くの場合,各部位の速度ピークの遅延発生を理由に運動連鎖が起こっている証拠とされることが多いが,体幹や下肢では遅延は少ないし,必ずしもその順序性がつねに観察されるわけでもない.順序性や遅延を示した論文は多く存在するが,そもそも何が伝達するのかそのメカニズムを示した研究は筆者の知る限りない(ムチ運動や多段式ロケットに似ているという話は散見されるが:補足5).
したがって動力が地面から伝達すると考え,振り子運動の連鎖(ムチ運動)のように遅延を発生させながら,つまり下肢から運動を先に起こそうなどと決して考えてはいけない.このような指導は,むしろ極めて「不自然な運動を誘導する」.動力を生成する部分では,遅延や振り子運動は物理的に意味がない.このことは,またどこかで詳しく述べることとする.
動力を生成する部位(投球では下肢と体幹)では,高速に運動する必要もなければ,振り子運動する必要もない.
自然な回転開始
投球においては肩より遠位の腕とボールは振り子とみなすことができる.ストレートの投球の場合,ボールも振り子として考えれば,ボールも腕に続く振り子と機能し,それがバックスピンという自然な運動を発生していることである.二重振り子ではなく,身体運動では珍しいが三重振り子として機能している(投球の力学メカニズム(2) −バックスピンは運動連鎖−参照).
なおバックスピンも,投球に限らずボールを制御しようと思うと自然に発生する運動である.ナックルのようにバックスピンを起こさないで投げようとするほど難しく,カーブなどの他の変化球は,このボールの自然な回転に抗うように回転を与えているので,ボールという振り子に関しては「自然さに逆らう球種」と言え,自然さに抗うほど,球速が低くなるという特徴もある.キック動作でも同様で,自然に発生してしまう運動である.
どの投げ方(スイング運動)にも共通だが,スイング運動の前半は根元側の振り子を加速する.しかし,その加速は,先端側の振り子にとっては逆方向の回転力を与えることになる.しかし,後半開始にその根元側の回転を緩めることで,次に先端側の振り子の回転を促している.
投球では最大外旋位やボールのスピン開始のタイミングが,その逆方向から順方向への回転へ切り替わるタイミングに相当する.筆者はゴルフスイングにおいて,それをナチュラルアンコックと呼んでいる(文献3).詳細なメカニズムを補足6に示す.
分散・分配による効率向上
投球が自然な運動と述べた理由は,動力を関節に作用する作用反作用の力を媒介として伝達するところにある.この自然さは効率と言い換えることもできる.ただしそれは動力の伝達効率ではなく,「大きな動力を発生できる余力のある部位で動力を生成し,それを伝達することで身体全体で負担を分散する」という意味である.たとえば小さな筋肉が全力をだすことは局所的でも疲労につながり,すぐに運動はいろいろな意味で破綻する.たとえ軽く投げるときでも,大きな動力を発生できる部位から,その動力を伝達することで,末端の弱い筋力を使わずに投げることができる.ここで述べる効率とは動力の分配と述べたほうが良いかもしれないが,ボールと指間に作用する力を,いかに身体側に分配するかということが課題となる.全力で運動する場合は,動力生成をより多くの部位で協調しながら運動することになる.
これは関節に作用するトルクを筋力に分配する方法と似ている.すなわち一つの関節には複数の筋肉が貢献するが,トルクから筋力への1対多の関係は,各筋肉の横断面積の二乗や三乗などに比例することが知られている.つまり,筋肉の強さに応じてトルクを各筋肉に分散させている.末端の負荷を身体全体で負担するという同じ原理が作用していると考えられる.
スポーツは身体運動の鑑
日常生活でこのような全力運動を行うことは多くないだろうが,負荷が大きくなると我々は自然と同じ原理から運動を行うことになる.この腕のスイング運動はスポーツ特有の特殊な運動であるが,ここで述べてきた理由からやはり投球運動はヒトにとって自然な運動といえる.
スポーツは「身体運動の特徴を顕在化」させる身体運動の鑑である.エリート選手の運動を観察すると,「正確性」「速度」などを最大化した結果を観察することができる.自然さがより顕在化するところが,スポーツの運動の特徴である.日常の身体運動では「ゆらぎ」が多く,その特徴は観察しにくい.身体運動の原理を研究したいなら,スポーツを対象として研究するのもよい.
おわりに
これまでと大きく異なり,この記事では「ヒトらしい運動とは?」という問いを投球運動を通して考えた.ここでは投球や身体運動におけるヒトらしさの特徴を述べたが,共通する重要な事実は,身体の各部位を接続する関節に作用する力(関節間力,内力)が,動力の伝達や動力生成の中心を担うことである.つまり身体運動の運動パターン形成におけるヒトらしさは,関節に作用する力を媒介して生成されている.
ここでは数理的な説明を最小限にとどめたが,これらは数理的に記述できる内容で,その多くはモーションキャプチャなどを用いた解析によって裏付けられている.ここで得られた解析結果は,まだまだ未解明のこともあるが制御ルールなどに落とし込むことができる.
ヒトらしさのルールを数理で記述できれば,異分野との融合を可能とし,ヒトらしい運動を生成する技術にもつながる.このようなアプローチはいまのところ教師信号が必要なAIにはできないが,運動の数理的な理解とAIが結びつけば,より面白いツールになっていくだろう.教師信号を生成し,ヒトらしく,またヒトにとっても可能な,未知の新しい投げ方を提案したり,より現実的なAIコーチが誕生する時代はさほど遠くないかもしれないが,その実現のためにはこのような数理的な理解が不可欠である.
補足
補足1:バックスピン
バスケットボールのシュートも,普通にシュートを打てばバックスピンとなる.回転を与えないように投げることはむしろ難しい.これは共通するボールの回転のメカニズムが作用するからである.一見するとバスケットボールのシュートは,直線的にボールを押しているように見えるが,ボールの軌道は曲がっており,大きな曲率半径の回転運動を伴いながらボールを投げている.このことから,投球と同様にボールには向心力が作用し,リリースに向かって押す力が最大値を超えて小さくなることで,ボールに作用する力の向きが下向きに変化することから,バックスピンが作用する.スポーツに限らずバックスピンは投げる動作で発生する自然な回転である.
記事「投球の力学メカニズム(2) −バックスピンは運動連鎖−」も参照されたい.
補足2:関節に作用する力による動力伝達
図A1:に示したが,部位AとB間の関節には部位BがAを押す力$\boldsymbol{f}$が作用する.一方,部位BにはAから押す力$-\boldsymbol{f}$が作用する.これらは関節をまたいで互いに反対向きの力が作用する作用反作用の力で,それらを足せば0となり消える(補足3).また,この関節の速度ベクトルは$\boldsymbol{v}$で運動している.すると,部位Aのエネルギーの単位時間あたりの変化(パワー)は部位Aに作用する力ベクトル$\boldsymbol{f}$と関節の速度ベクトル$\boldsymbol{v}$との内積で与えられる.もし,この$\boldsymbol{f}$と$\boldsymbol{v}$の向きがおおよそ同じであるなら,部位Aのエネルギー変化は$\boldsymbol{f}^T\boldsymbol{v} > 0$となる.ベクトルの内積であるので,この値はスカラである.
一方,部位Bのエネルギー変化は$-\boldsymbol{f}^T\boldsymbol{v} < 0$となり,部位Bは同じ大きさだがエネルギーが同じ量だけ減少することになる.
このことから関節に力が作用し,運動が発生すると(速度を持つと),関節を通じてエネルギーの移動が起こる.具体的には単位時間あたりに$\boldsymbol{f}^T\boldsymbol{v}$だけ部位AからBへエネルギーが伝達することになる.

図A1:関節に作用する力による動力伝達
補足3:内力
図3や図A1のように関節に作用反作用の力が作用する.部位AとBの系内でこれらの力を加算すると0となる.仕事レベルで考えても,この部位AとBの系内では作用反作用の力の媒介によるエネルギーの移動があっても,AとBの系全体に対して何も仕事をしない力を内力と呼ぶ.一方,外力は系の外との相互作用で,系のエネルギー変化を引き起こす.もし部位Aだけを系として考える場合,系外の部位Bから系内の部位Aに作用する力は外力である.系の範囲の定義によって内力か外力が変化するので注意されたい.
補足4:アクチュエータの有無とスイング運動の関係
システムの観点から補足する.
ハンマーと手の間には筋肉(アクチュエータ)がなく,左右の腕全体とハンマーから構成される二重振り子とみなすことができる(文献・資料).制御工学ではこれを自由度よりもアクチュエータの数が少ないシステムという意味で劣駆動系(under-actuated system)と呼ぶ.過去の記事(身体における運動パターン形成 #3 〜ハンマー投〜)も参照されたい.
ゴルフスイングも,両腕(左右の手+前腕+上腕を一つの振り子と見立てる)とクラブを二重振り子と見立てることができ,クラブと手間に筋肉による回転力が加わり全ての自由度(関節)にアクチュエータが備わる(これをfull-acutuated systemと呼ぶ)が,それでも関節に作用する力が,クラブやハンマーを回転させる動力伝達の中心を担うことに変わりない).

図A2:(a)ハンマー投(劣駆動系).(b)ゴルフスイング(full-acutuated system)
補足5:多段式ロケットとムチ運動
運動連鎖のたとえとして,多段式ロケットやムチの運動とのアナロジーから各部位の運動の遅延が必要となるという議論がある.
しかしこれは誤りである.多段式ロケットは1段目のロケットの燃料を使い切り,その目的が終了してから,むだな1段目を切り離すことで,動力を上のロケットに伝達する.
ムチ運動の場合は,動力源は根元だけで,運動が完全に止まることで,次の部位に伝達している.
身体運動では動力発生時に運動を止める必要もない.常に全身で動力を末端に供給し続ければよい.ロケットやムチとは事情が全く異なる.
補足6:自然な回転開始
図A3(a)(b)にはAとBの振り子から構成される二重振り子を示した.この二重振り子運動を行っている最中,先端の振り子Bに作用する2つの反対方向の回転力が作用する.
(a)は根元側の振り子Aを順方向(投球方向)に回転させると,先端側のBでは逆方向に回転力が作用することを示している.すなわち回転力の接線方向成分はBの根元側では投球方向を向いているが,先端側では反対方向の加速を引き起こす.バットを回そうと腕を回すとバットは後ろに戻ろうとするの現象と同じである.投球では,前半手やボールは後方に引っ張られてしまうことに相当する.ただし,肩関節の可動域から最大外旋位を超えることはない.いわばストッパーの構造があり,筋力を発揮せずに固定することができる.
(b)はそれと直交する方向の力で振り子Aから振り子Bに向心力が作用することを示している.つまりAがBを引っ張る形になるが,この向心力の接線成分が順方向の加速を生成する.Bの先端の遠心力と,Aからの向心力で,2つの振り子がまっすぐになろうとしているだけである.
スイング運動中(a)(b)の2つの反対方向の加速力は比較的拮抗しているが,振り子A(投球では腕)を加速させている間は(a)の逆方向の力が優勢である.ところが,(a)の回転力を少し緩めて(止める必要はない)最大値を迎えると,(b)の順方向の回転力が優勢となる.最大外旋位は肩の加速度の投球方向成分の最大値とほぼ一致する.この切り替わるタイミングが最大外旋位である.ボールを含め,三重振り子と考えると,ボールの回転開始も同じ原理で説明される.つまり,ボールのスピンはボールに作用する投球方向の力が最大値をむかえることで開始する.ボールも力の作用点からぶら下がっている振り子と考えて良い.
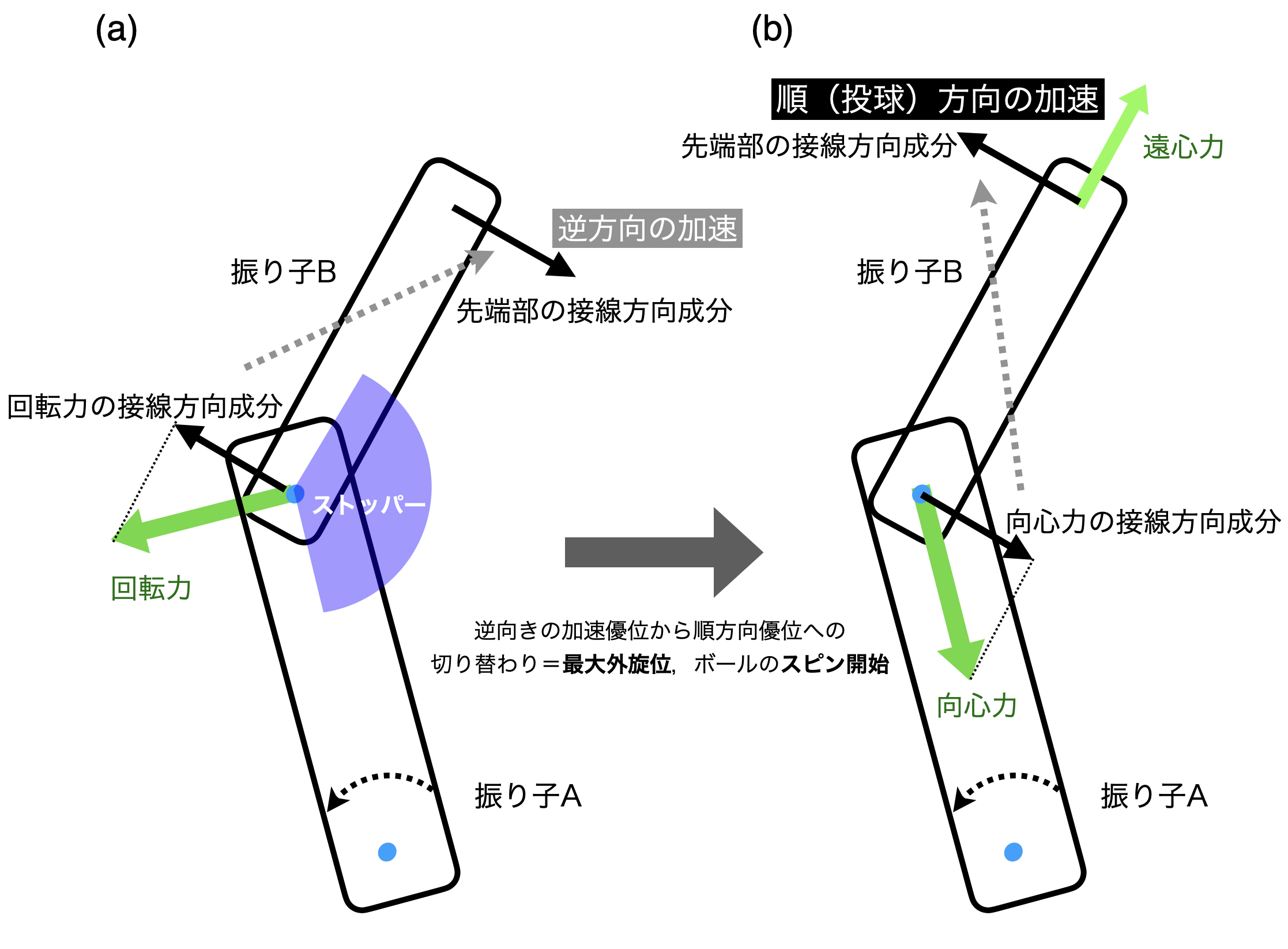
図A3:スイング運動中,振り子には順方向と逆方向の両方向の回転力が作用する.
(a)逆方向の加速:スイング前半この加速力が優位.振り子Aの角加速度がBの逆方向の回転を生成.
(b)順方向の加速:後半この加速が優位.振り子AがBに作用する向心力が順方向の加速を生成.
参考文献
1)太田,梅垣,室伏,羅,二重振子のパラメータ励振原理によるハンマー投運動の数理解析 ,日本機械学会シンポジウム:スポーツ・アンド・ヒューマンダイナミクス講演論文集,pp.319-324,2010
2)太田,梅垣,室伏,羅,ハンマー投のダイナミクスに基づくサイバネティック・トレーニング ,バイオメカニクス研究,Vol.17,No.1,pp.26-36,2013
3)太田,仰木,澁谷,ゴルフスイングにおける内力を利用したエネルギー伝達,シンポジウム: スポーツ・アンド・ヒューマン・ダイナミクス講演論文集,2012, pp.293-298
4)尾崎,太田,神事,二重振子モデルに基づいたキック動作の数理解析,日本機械学会シンポジウム: スポーツ・アンド・ヒューマン・ダイナミクス講演論文集,2011, pp.453-458