はじめに
これまで一般的な投球の力学について述べてきた.ここでは,特にストレート(4 seam, ファストボール)の投球の力学メカニズムの詳細について考えていきたい.その前に,これまで述べてきた投球の力学メカニズムを簡単にまとめるが,詳細は前章までの記事を参照していただきたい.
力学の話しでわかりにくい部分も多いかもしれないが,この記事の後半に示す計測結果のアニメーションは,実際にボールにどのように力を作用させて回転しているかを示しているので,それだけでも面白いのではないだろうか.
データの公開を許していただいた被験者の方に御礼申し上げる.
復習1:回転制御フェーズにおけるボールの力学挙動
そもそも,目的の方向に投げることができなくては運動の目的を達成できないため,末端のボールと手間の力学が身体全体の運動を強力に拘束する.したがって,野球に限らずバイオメカニクスの研究は,道具などを接触する末端から理解していくことが重要だ.というよりも,それを理解せずに全身の力学を理解することはできるのだろうか?
ここでは,まず,約130km/hのストレートの投球(投球1)の計測例を見ながら,投球の力学メカニズムを復習する.

図1:真上から見た投球1のボールの軌跡(1kHz)(最大外旋位〜リリース)
回転制御フェ−ズ(バックスピンの回転力発生〜スピン開始〜リリース:紫色の領域)
角速度ベクトルは長さが角速度の大きさを示し,太い軸方向が右ネジ方向
ストレートのリリース前のボールの制御は,ボールにバックスピン(BS)の回転力(モーメント)が作用し始めてからリリースまでの回転制御フェーズの間に行われる.さらに回転制御フェーズはバックスピン開始を境にして前後に分けることができる(図1).
回転制御フェーズ前半(BSモーメント発生〜スピン開始:5ms程度):
前半は「トップスピンの勢いをとめるフェーズ」である.後半にバックスピンが始まるが,前半も重要なフェーズである.ハイスピードカメラなどで観察してもボールはあまり回転していないので,見過ごされるだろう.130 km/hの投球では,この間に約10km/h球速が増加する.
回転制御フェーズ後半(10ms程度):
「母指が離脱」し(親指がボールから離れ),実際に「スピン回転」を始めることで後半が始まる.この間に2000rpm程度までに一気に増加し,リリース前の後半も球速が約10km/h増加する.「バックスピンのフェーズ」である.
回転開始とリリースのトリガー
回転制御フェーズは,「バックスピンの回転力(モーメント)を与え始める」ことで始まる(後ほど図6のグラフでも確認されたい).図1のBSモーメント発生の時間である.回転制御フェーズ前半では緩やかなトップスピンの状態が続く.このため前半の間にトップスピンの勢いを相殺することで,後半のバックスピンスピン回転が始まる.バックスピン(BS)開始は母指の離脱とほぼ同時である.

図2:バックスピンの回転力(モーメント)は力の向きの変化によって発生
力ベクトルが中心を向く場合,トルクは発生しない.
中心よりも上を向く場合,トップスピンのトルクが作用する.

図3:投球方向の力の減少が下向きの力に変化することで,バックスピンの力が発生(b:投球1).
このバックスピンの回転力(モーメント)は図2のように,「ボールに作用する力が下向きに変化」することで作用する.さらに,この下向きの力への変化は,向心力はあまり変化しないが(むしろ少し増加する),「投球方向への加速力が最大値に達し,減少し始める」ことで発生する(図3).
投球方向に作用する力と向心力
バックスピン開始のトリガーは,投球方向の加速力の減少だが,投球方向に作用する力とは一体なんだろうか?
ボールに作用する力は投球方向に作用する力と向心力に分解できる(あまり一般的ではない座標系の取り方をするので,力学に関心のある方は,詳細は投球の力学の基礎(1) -ボールに作用する力とボールの挙動:質点の力学-や,補足1を参照されたい).
図3の投球方向の加速力は,ボールに作用する力$\boldsymbol{f}$のうち,投球方向(ボールの速度方向,接線方向)に作用する成分で,「球速を増加させる力」である.一方,向心力はこれに直交し,ボールの回転運動を維持するための力として機能する.青色のボールに作用する力$\boldsymbol{f}$は向心力と投球方向の力の合力で,この章の後半でも示すが,合力$\boldsymbol{f}$はボールを回転させる力として作用し,この力が下向きに作用することでバックスピンの回転力となる.回転制御フェーズから投球方向の加速力は減少しはじめるが,バックスピンの回転力も発生するので,『回転制御フェーズは「球速」と「回転数」ともに増加する重要なフェーズ』である.
この「投球方向の力が最大値に達する」ためには,ボールに与える力を緩めることで十分であって,ブレーキをかける必要はない.また,手先の操作で始まるわけではない.ただし,把持力の与え方・握り方がボールの制御に重要な影響を与えるが,母指を離すというよりは,摩擦でボールを把持する力よりもバックスピンのモーメントが大きくなり,「自然と母指からボールが離脱していく」と表現するほうが適切だろう.
なお,ボールの回転開始がリリースを促すが,リリースへとつながるその回転開始は,手先ではなく全身の力学で引き起こされていることに注意をしていただきたい.恐らくこのときに地面反力が極大となっているはずだ.今回はボールの力学を中心に述べているため,このことについてはまたどこかで述べる.
復習2:バックスピンは転がり

図4:ストレートは回転制御フェーズにおいて「転がり」を行う
「投球の力学メカニズム(1) ー母指の離脱はバックスピンを誘発しない−」で述べたように,回転制御中のバックスピンの回転は転がりが主体である.投球中,ボールの外から力の作用点(接触点と考えてよい)を眺めると,ボールの中心から常に同じ方向(斜め上)を向いている.このような現象をここで転がりと呼んでいる.ここで述べる転がりとは,板の上をボールが転がっているイメージで,板の代わりに指の上を転がっていると考えればよい(図4).ただし,指の長さという拘束が発生し,転がす時間・距離に上限が発生する.
転がりは球速と回転数ともに増加させる
ストレートは,ボールが「転がる」がゆえに,前述の『「球速」と「回転数」ともに増加させる』ことができる.
これらの理解のもと,次にストレートの制球(投球方向の制御)と回転の制御について考えていきたい.
ストレートの回転制御フェーズ中の力学挙動
速度と角速度

図5:ボールの速度と角速度(回転速度).黒の実線は各ベクトルのノルム(大きさ)(投球1).
図5は,投球1のボールの速度と角速度を示したグラフである.わずか18 ms程度の短い時間の回転制御フェーズで速度が110から130 km/hまで増加し,スピン開始のところから,左右($y$)軸まわりの回転の向きが変化し,バックスピンが開始し,一気に2000rpm(約200 rad/s)まで増加している.
なお,リリース前後の角速度は一定値に収束するはずだが,ゆらいでおり若干精度が低い.
力とトルク

図6:ボールに作用する力とトルク.黒の実線は各ベクトルのノルム(大きさ)(投球1).
図6は,投球1のボールに作用する力とトルクを示したグラフである.BSモーメント発生(回転制御フェーズの開始)の時点で力のノルム(大きさ:実線)が最大値となっている,このときxy成分は減少しているが,z成分(下向き成分)の大きさはさらに大きくなり,力ベクトルの向きが変化している.$\tau$(ねじりモーメント)についてはカーブ(次章)で説明する.
一方,トルクは回転制御フェーズの開始(BSモーメント発生)時点から急激に大きくなり,バックスピンの開始時点で最大値を迎えている.
ただし,たとえこれらのデータを3次元空間にベクトルとして表現しても,ボールをどのように制御しているかメカニズムを理解することは困難で.次に示す力の作用点で力ベクトルを可視化することによって,制御メカニズムの理解をより容易にする.
なお,図5のリリース前後の角速度の精度の低さがトルクにも現れ,本来はリリース前のトルクはより小さい値のはずで,その影響は次の力の作用点の位置の精度にも影響する.
力の作用点
力の作用点と転がり
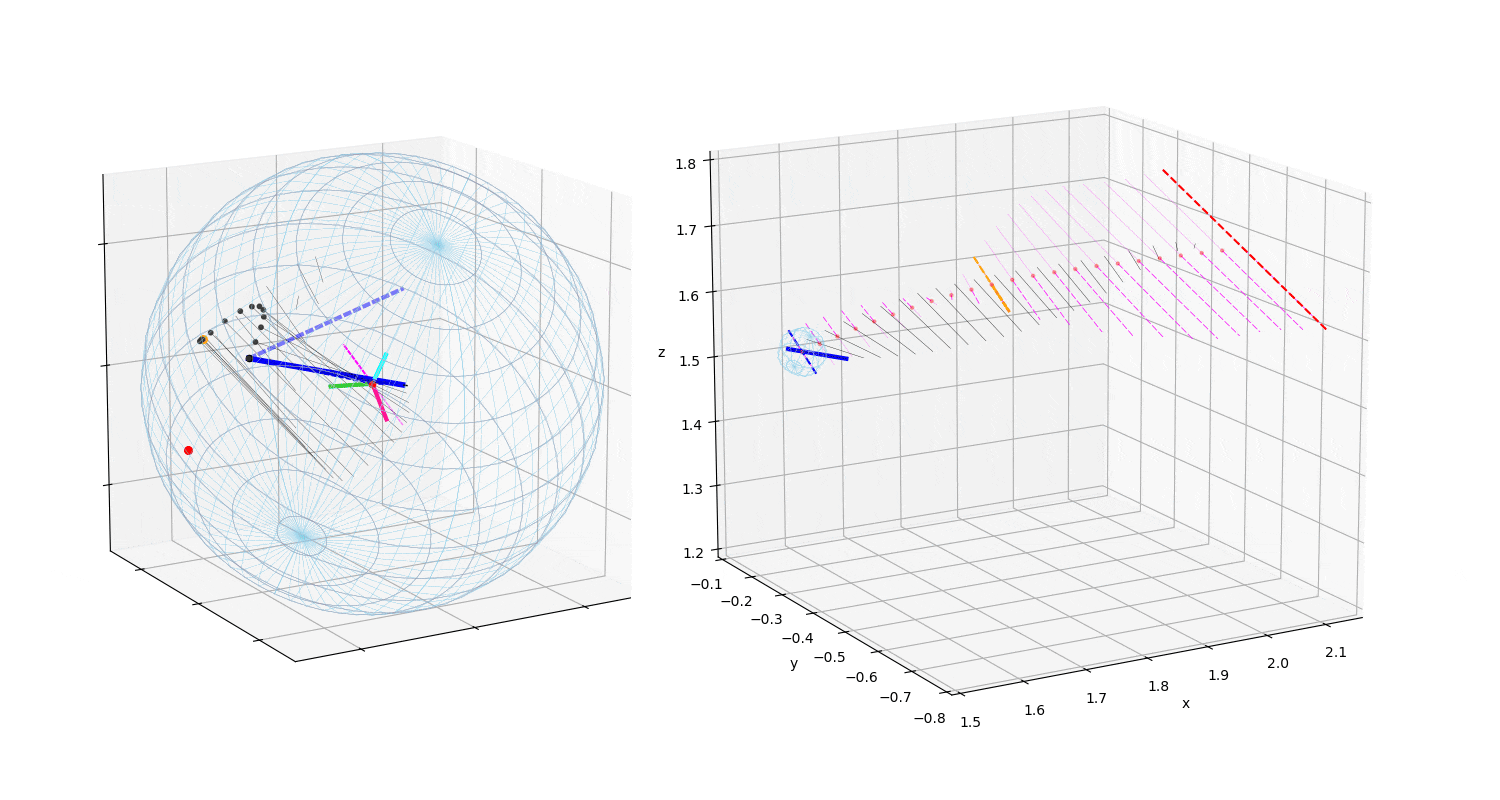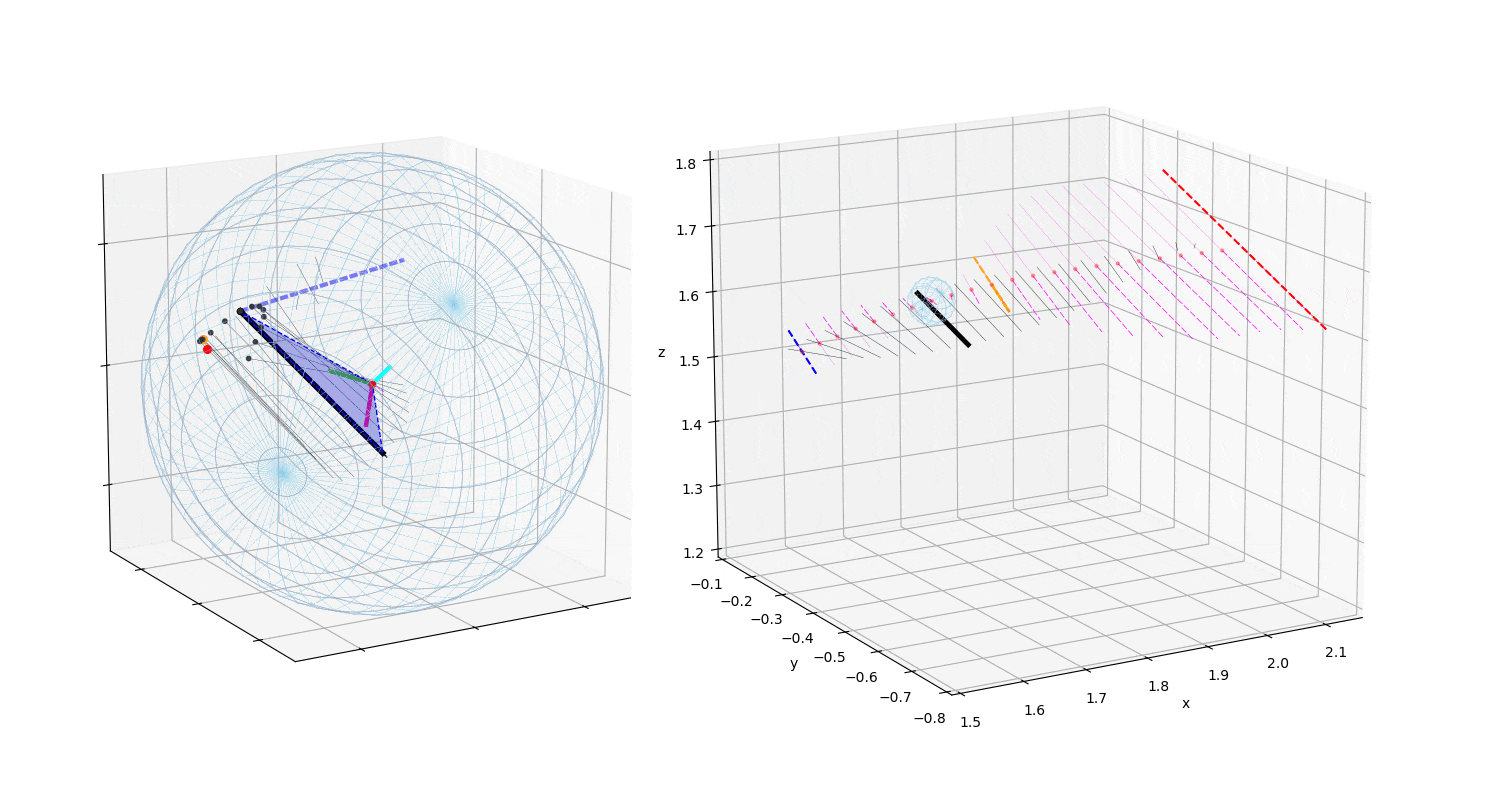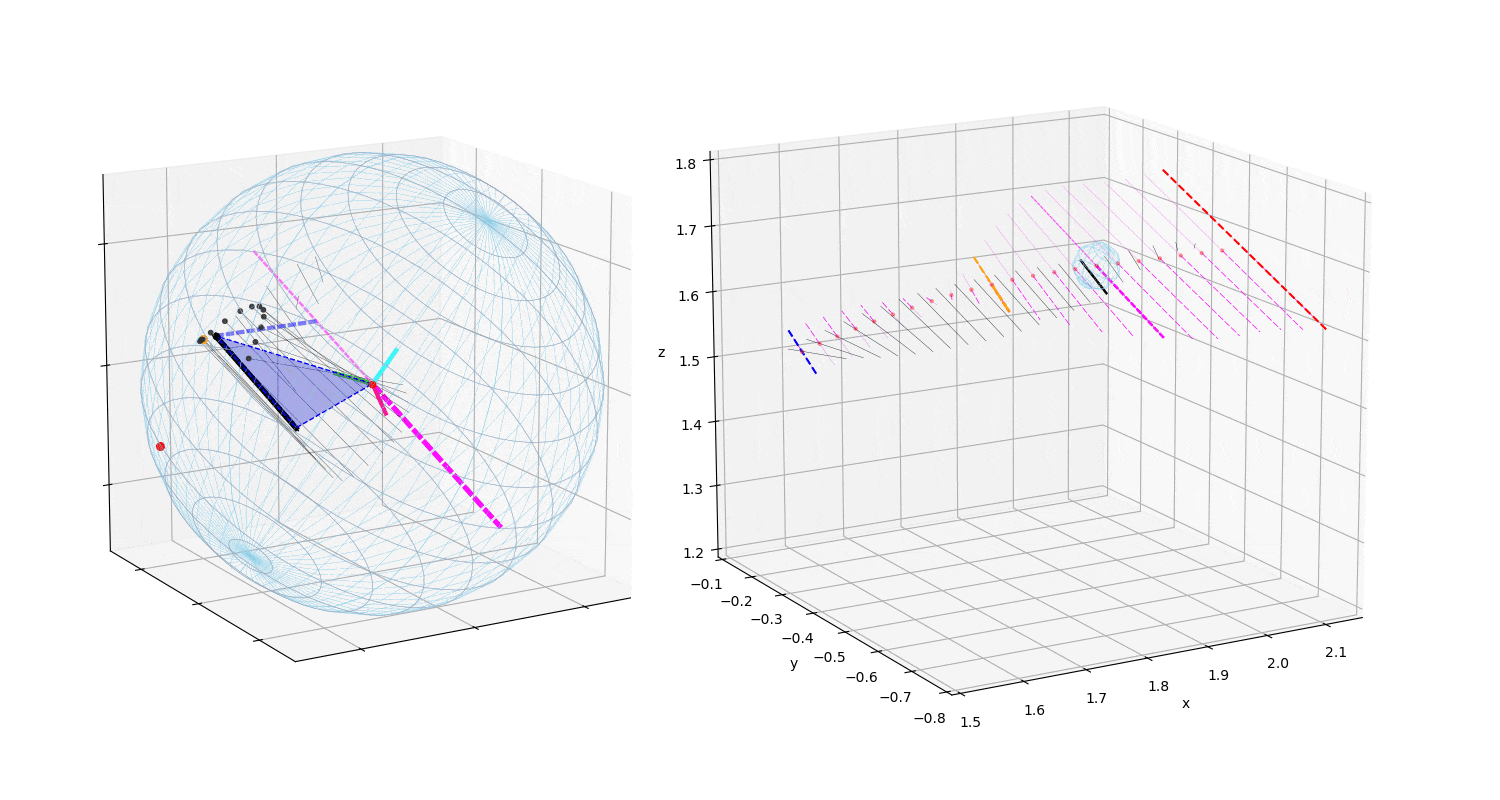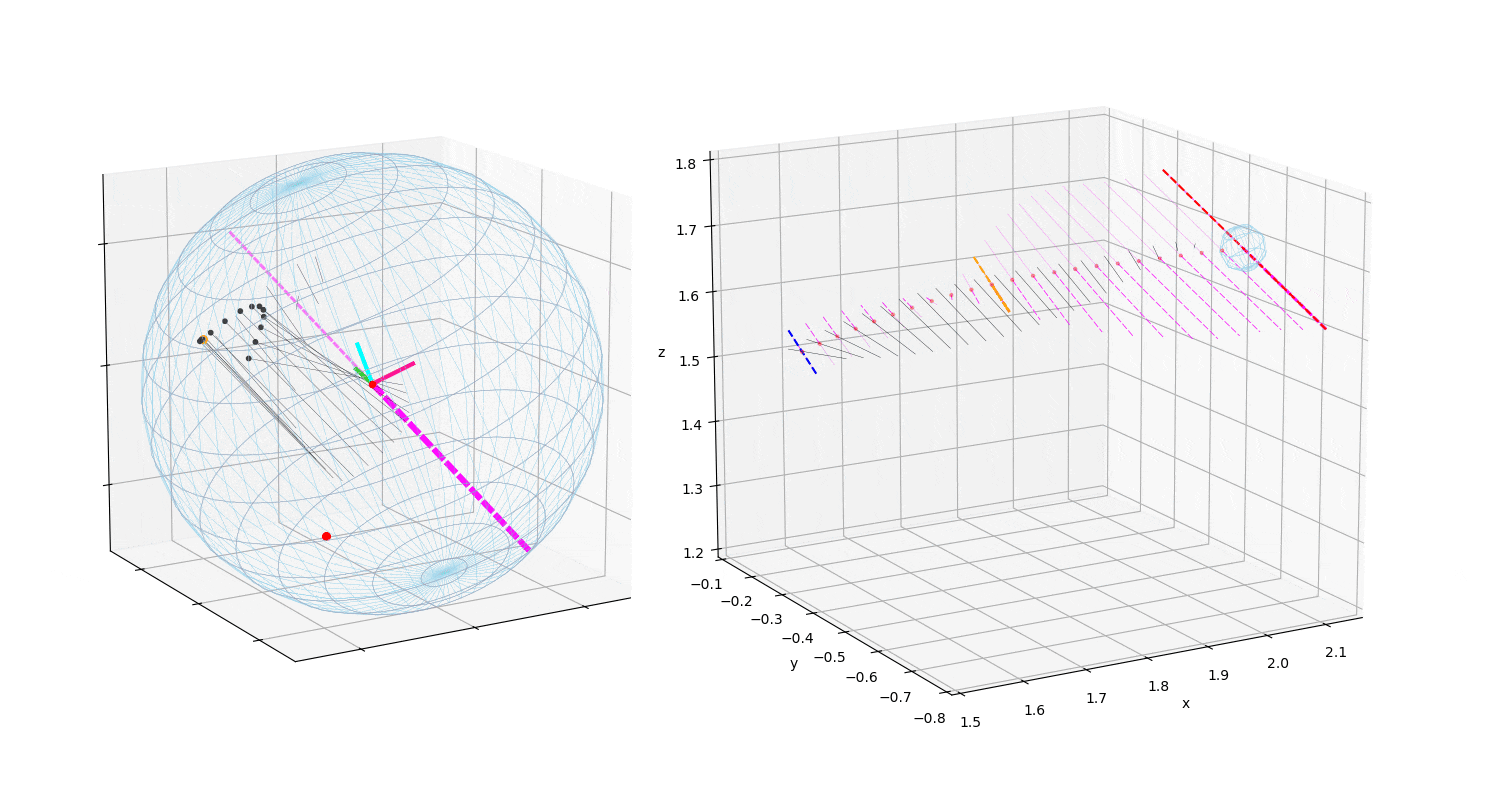
ストレートの投球の制御の特徴は転がりである.まずこの様子をアニメーションで示す(投球1).
なお,リリース近く(動画の最後の数フレーム)なると,力の作用点の位置が上側に移動しているが,指の位置を考えれば恐らく実際の力の作用点は下側に移動している.これはリリース前のトルクの計算精度の低さに起因する.
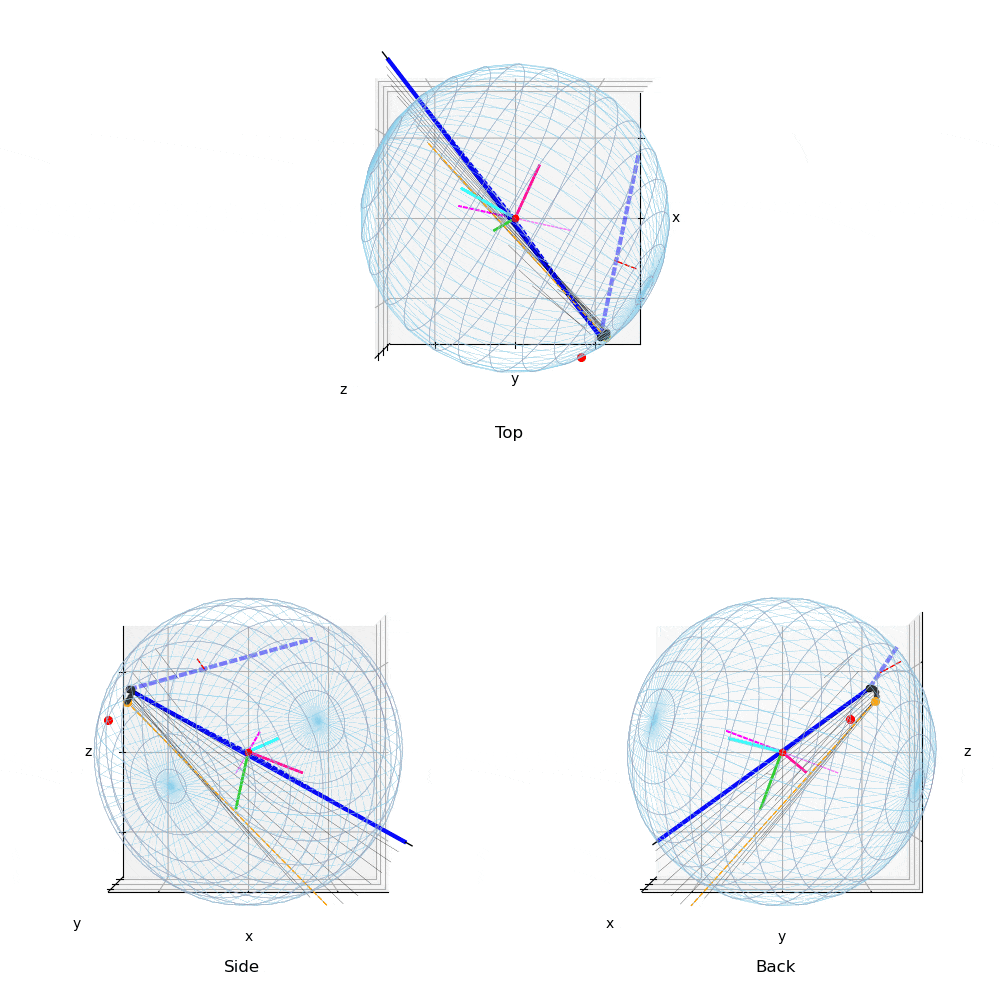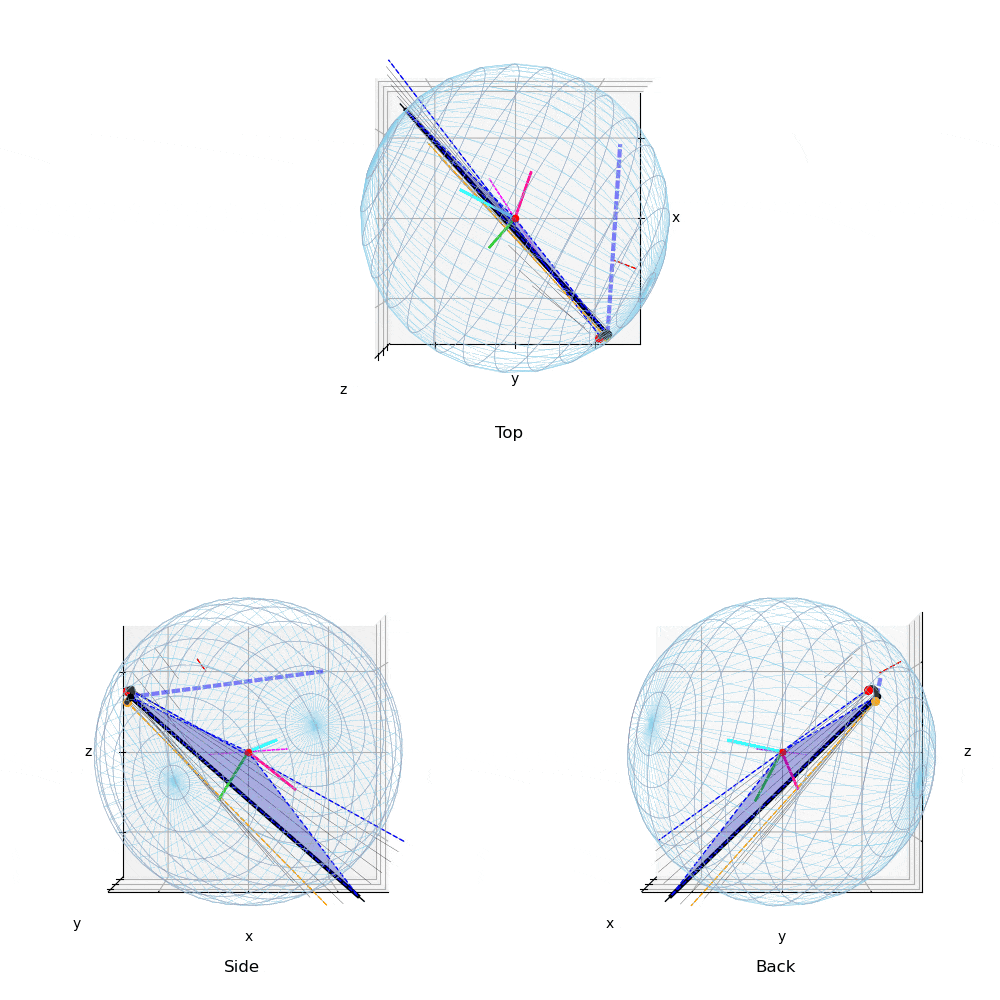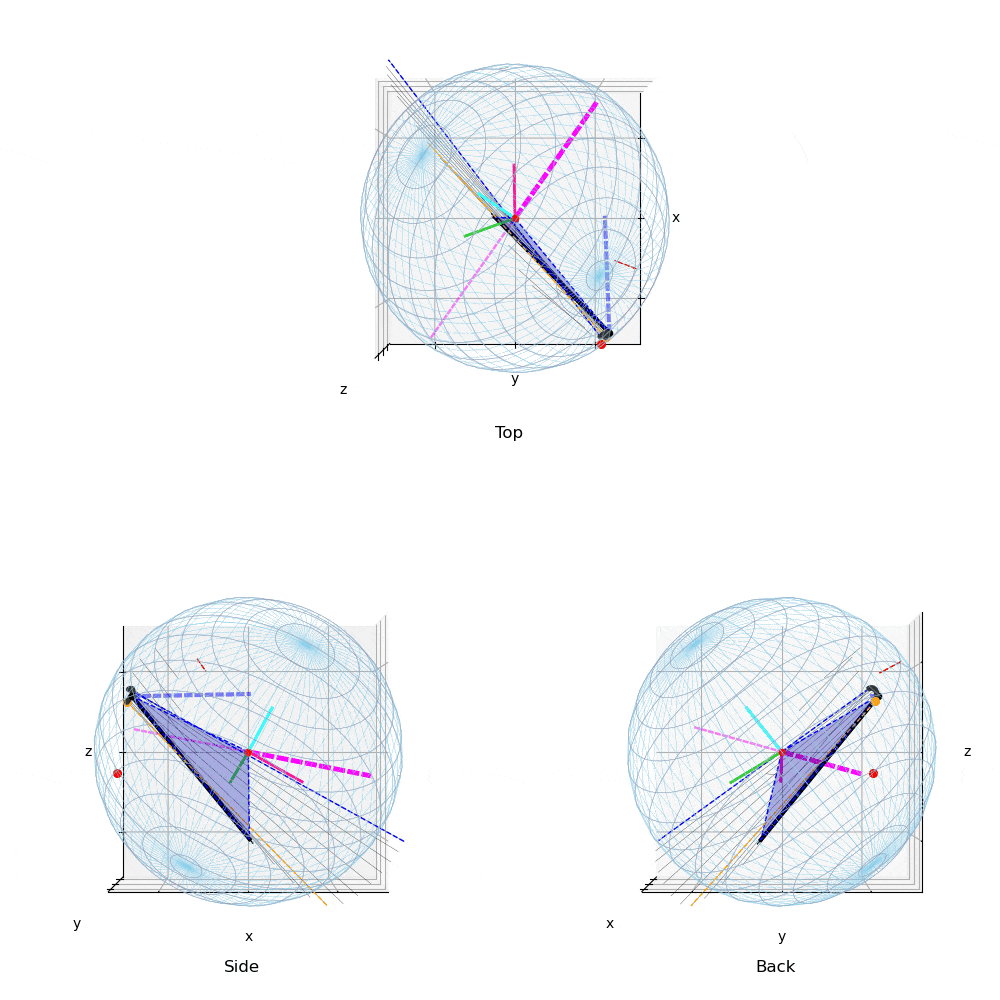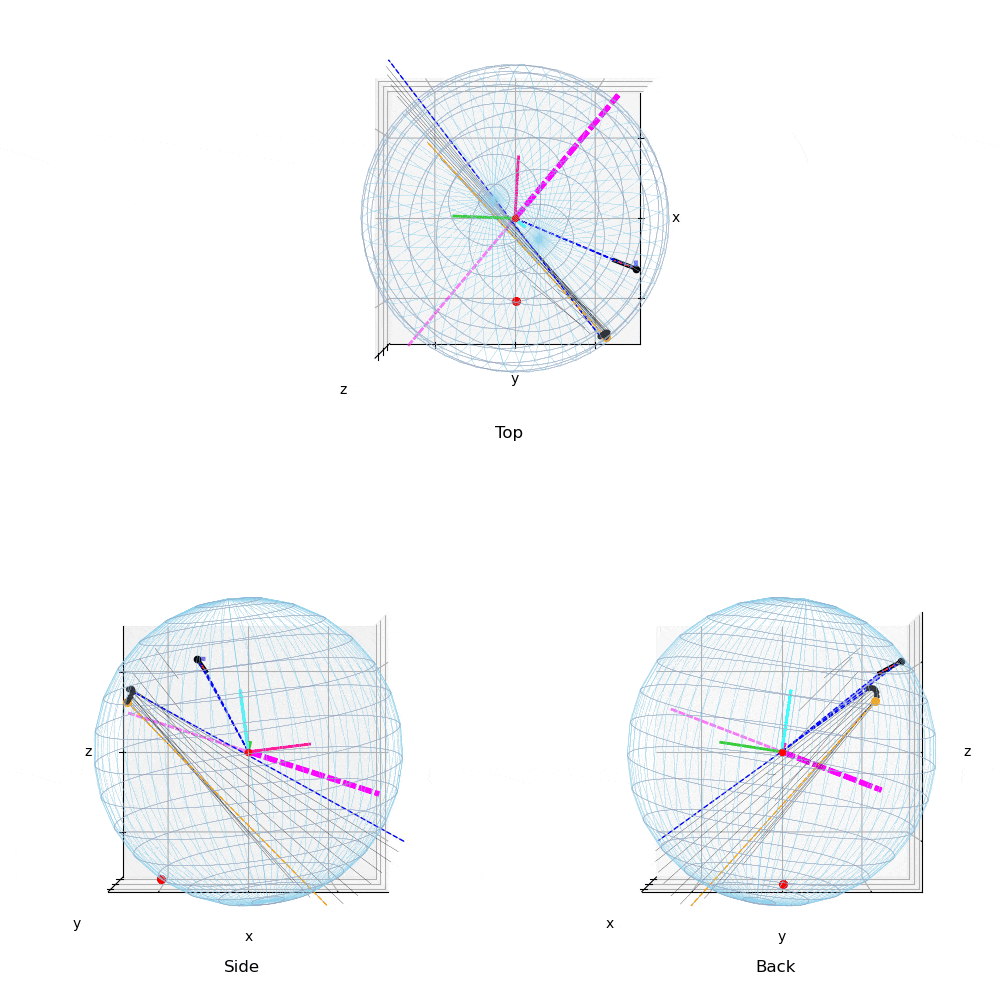
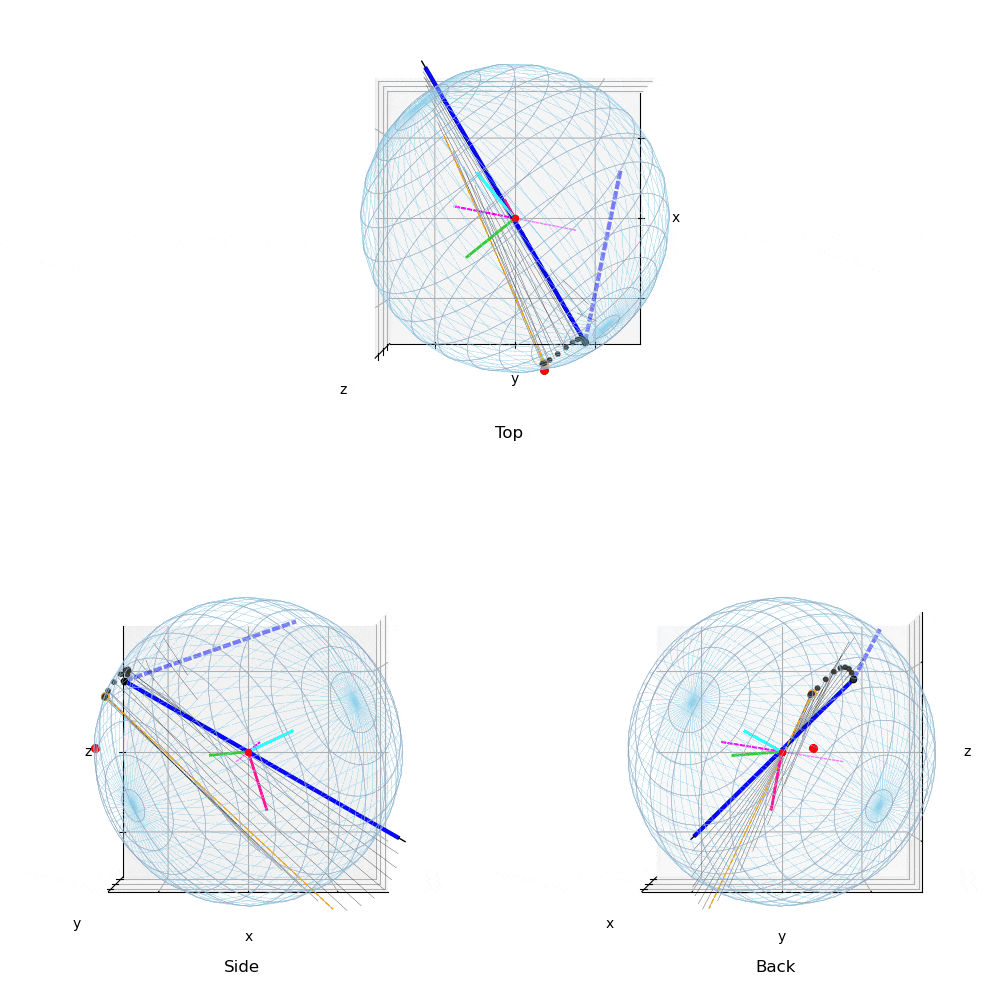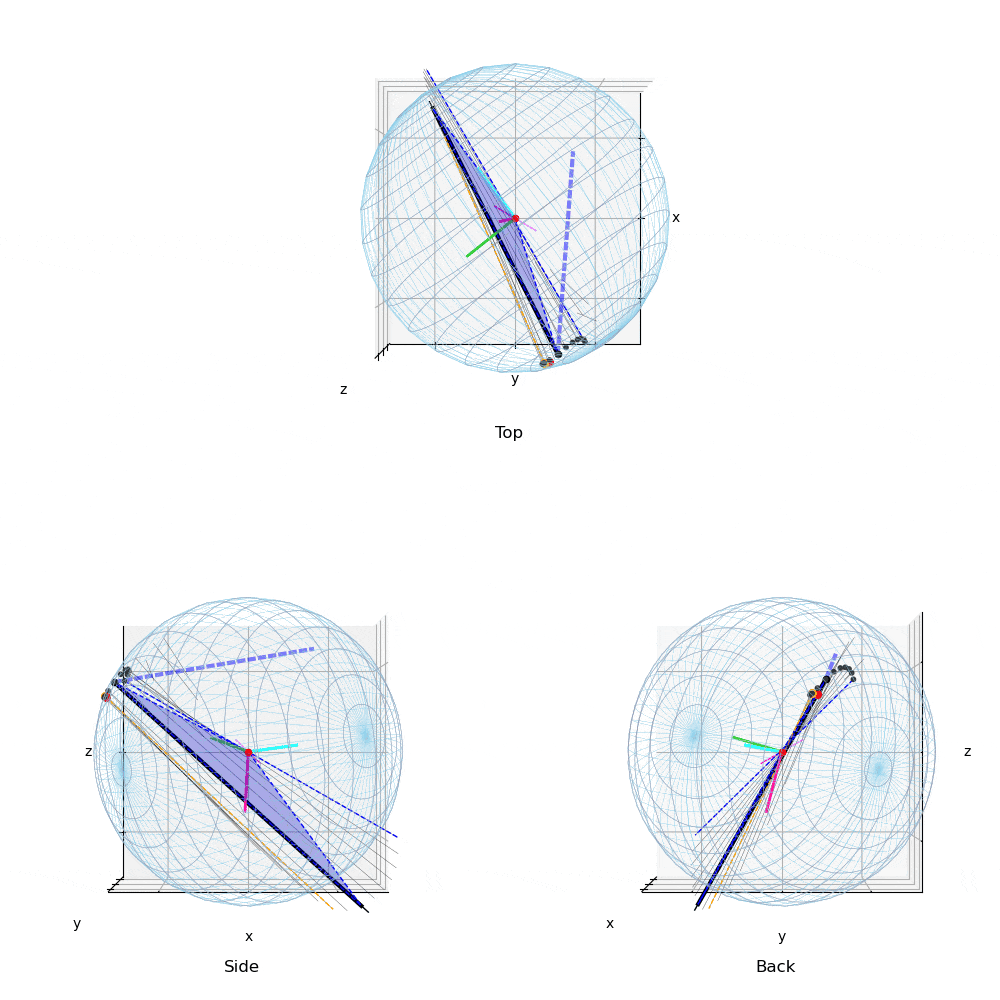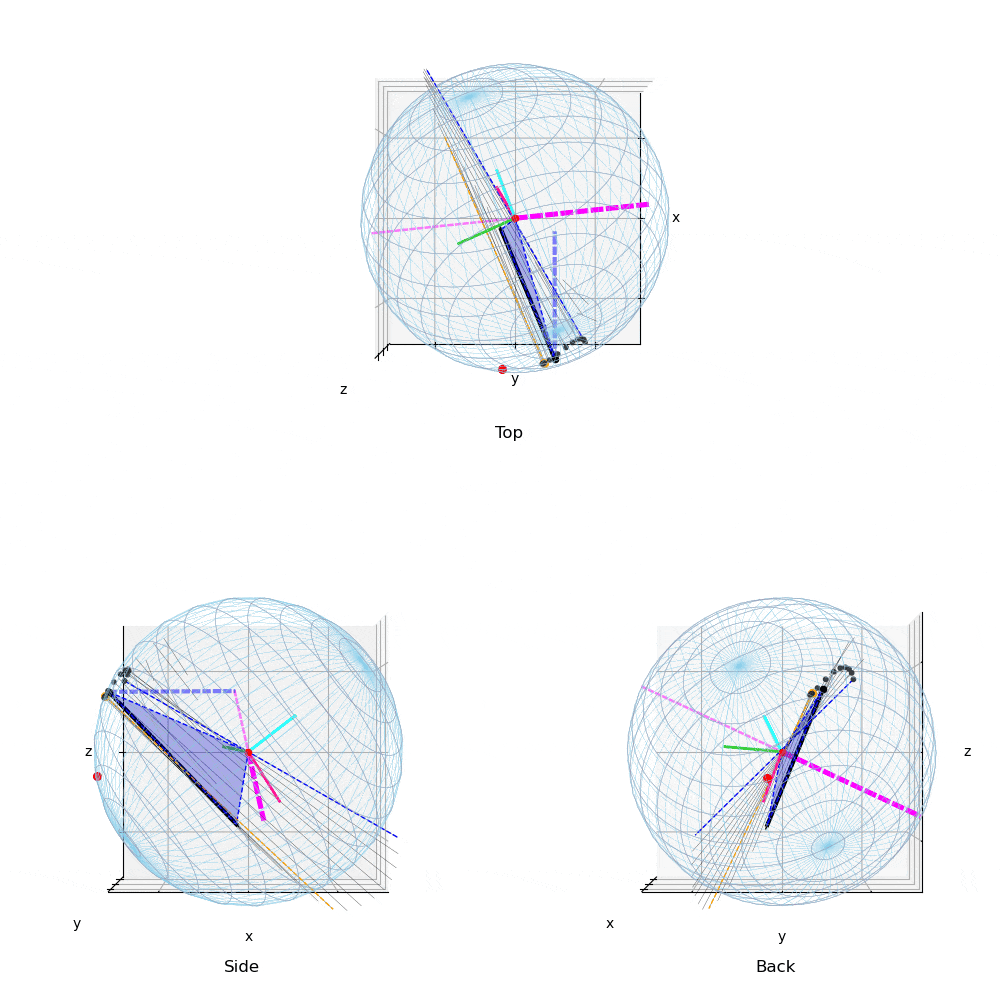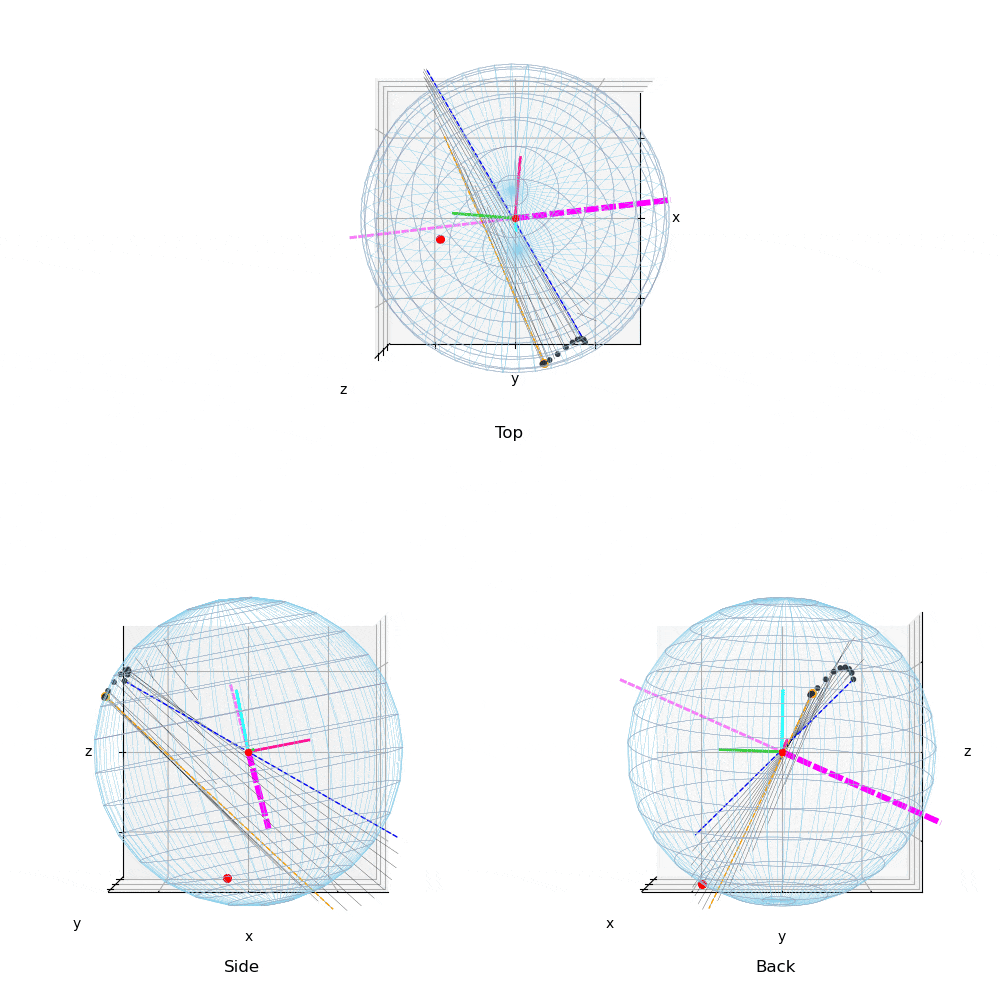
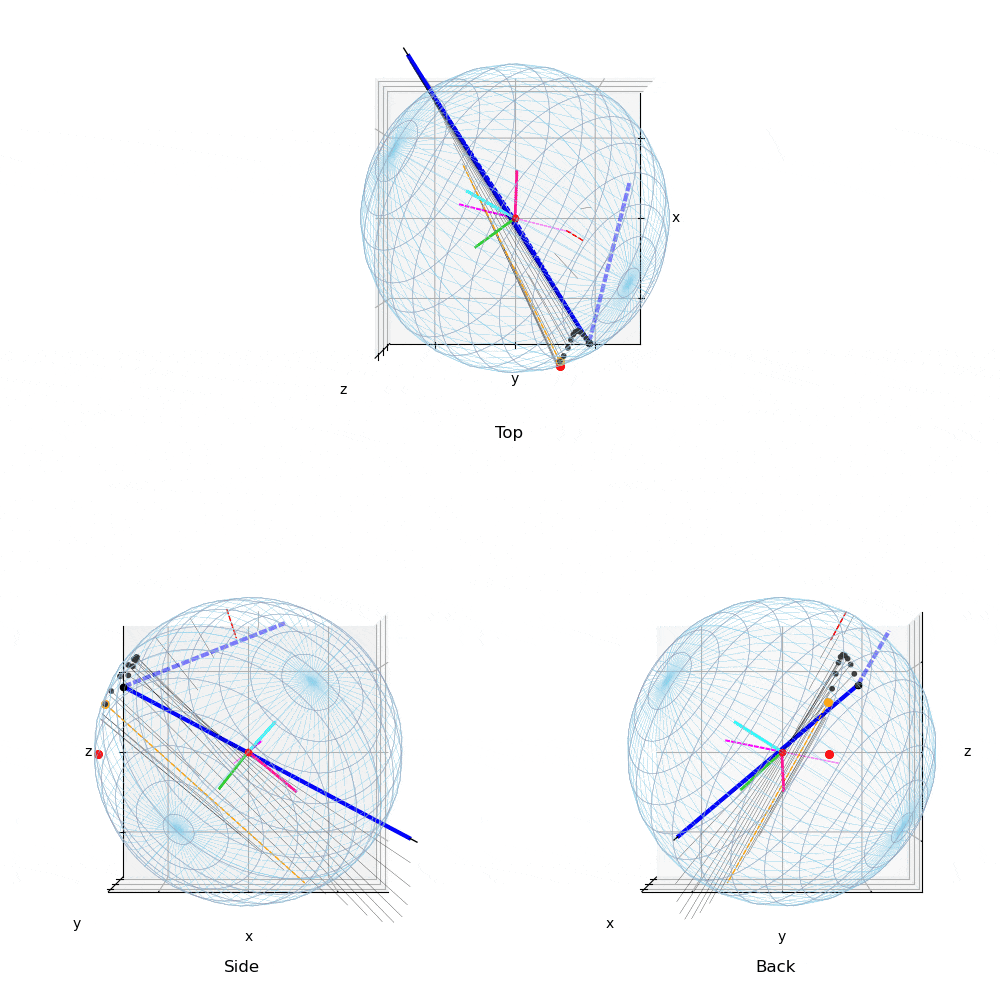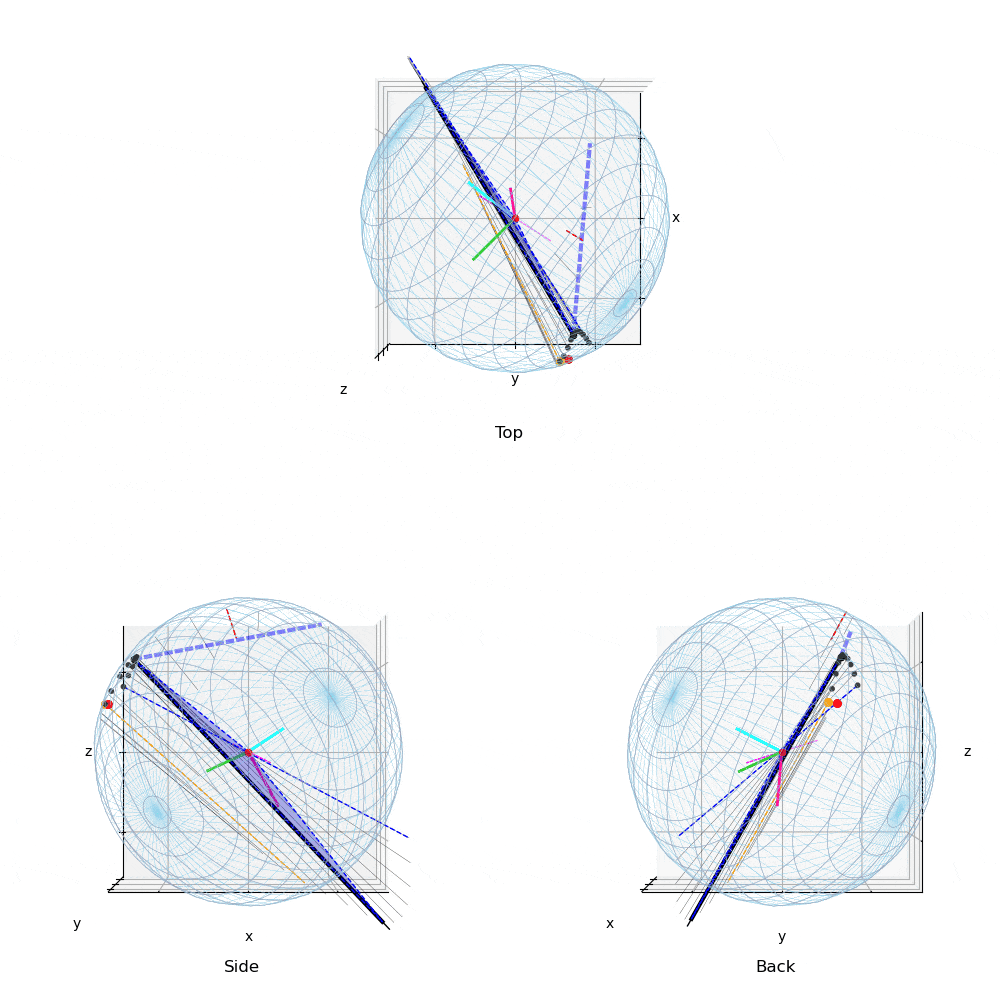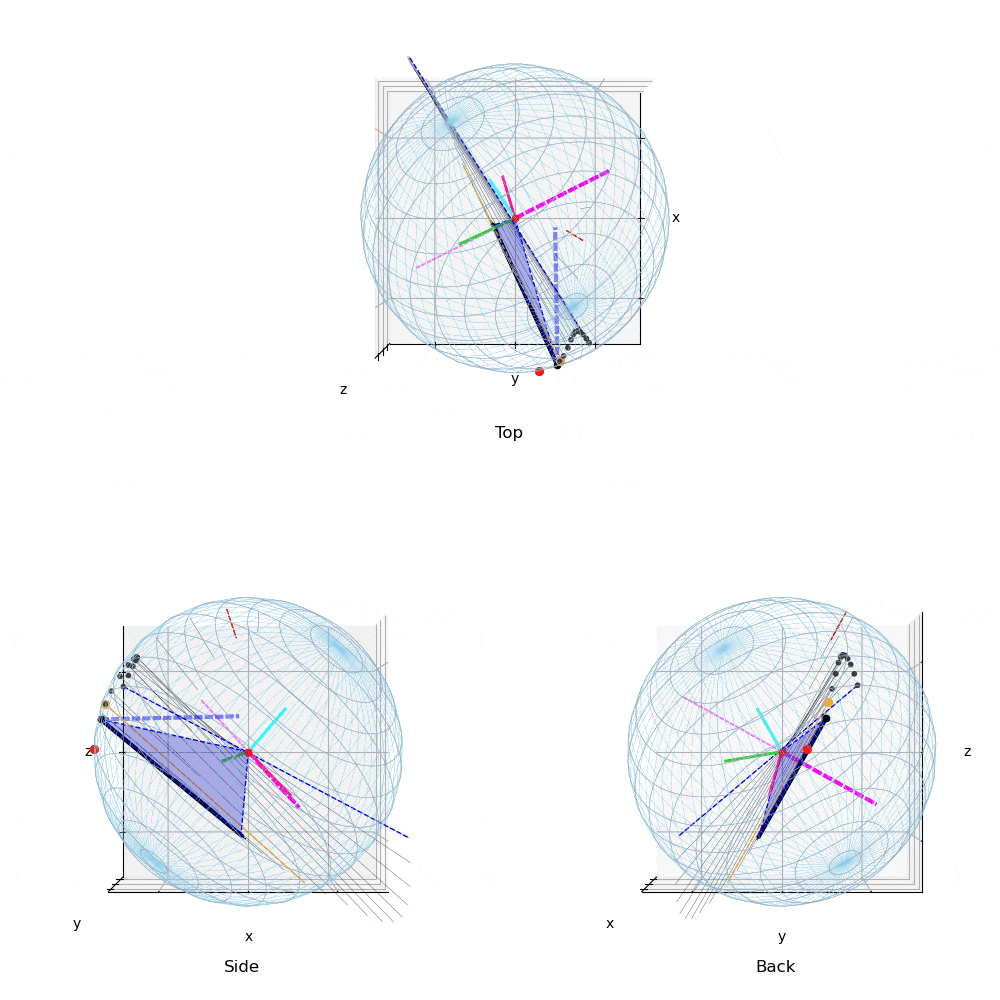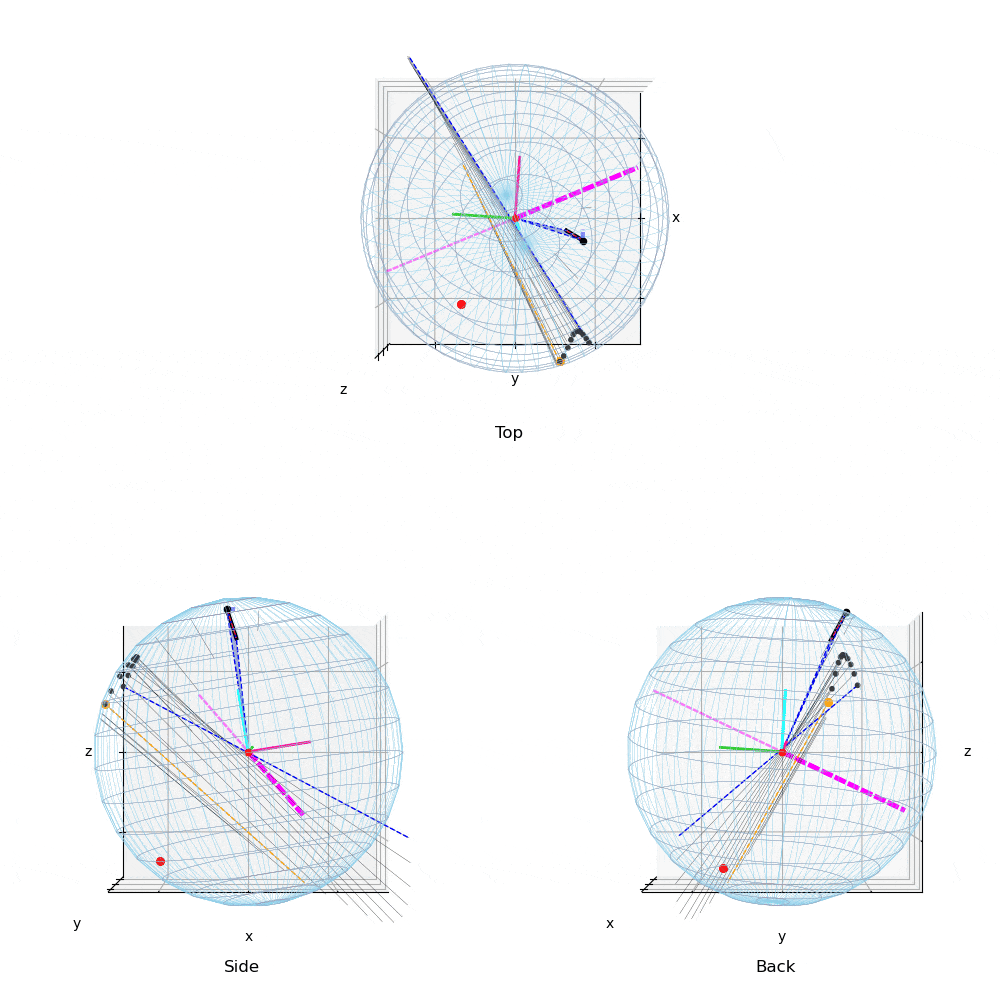
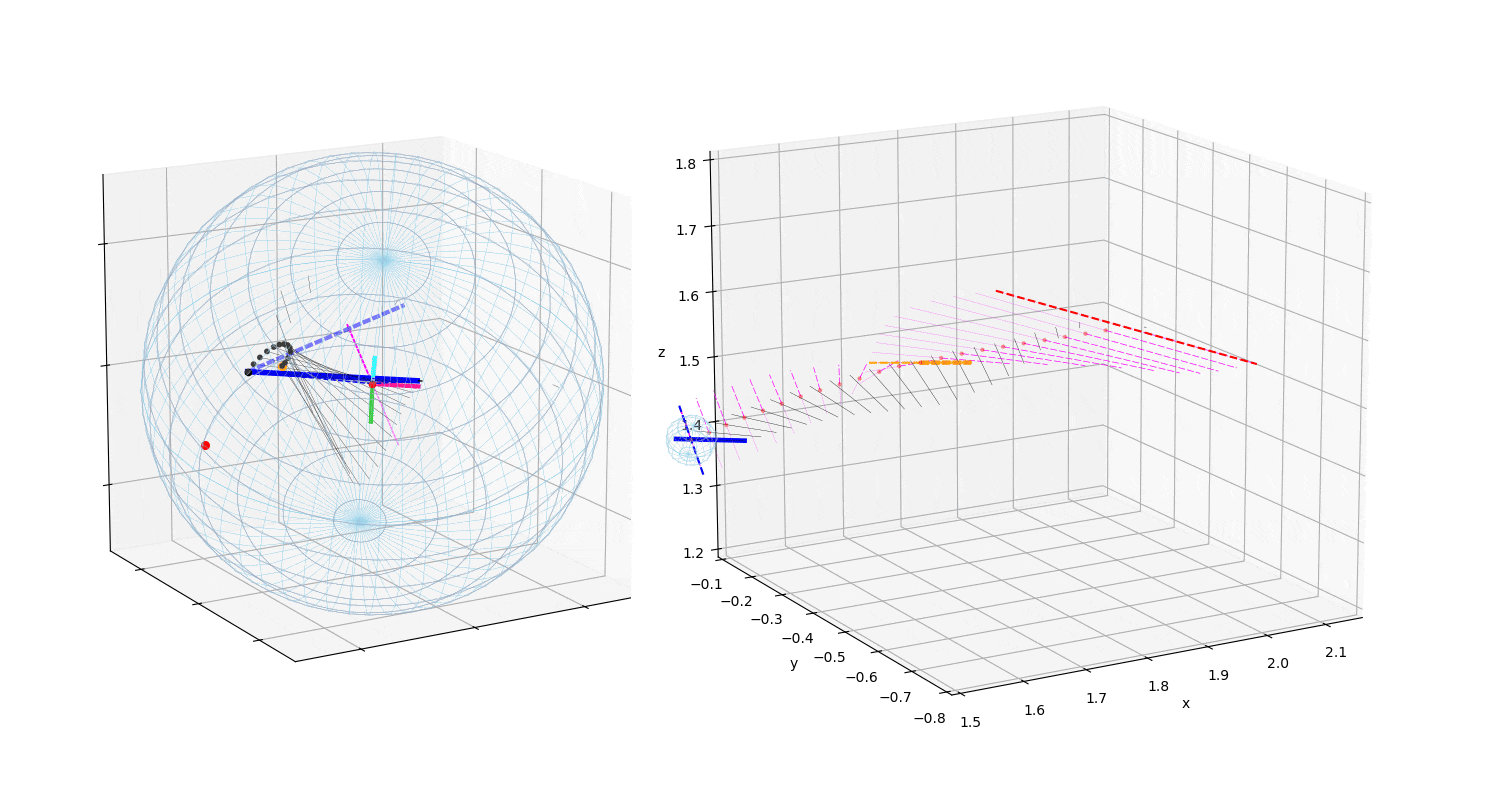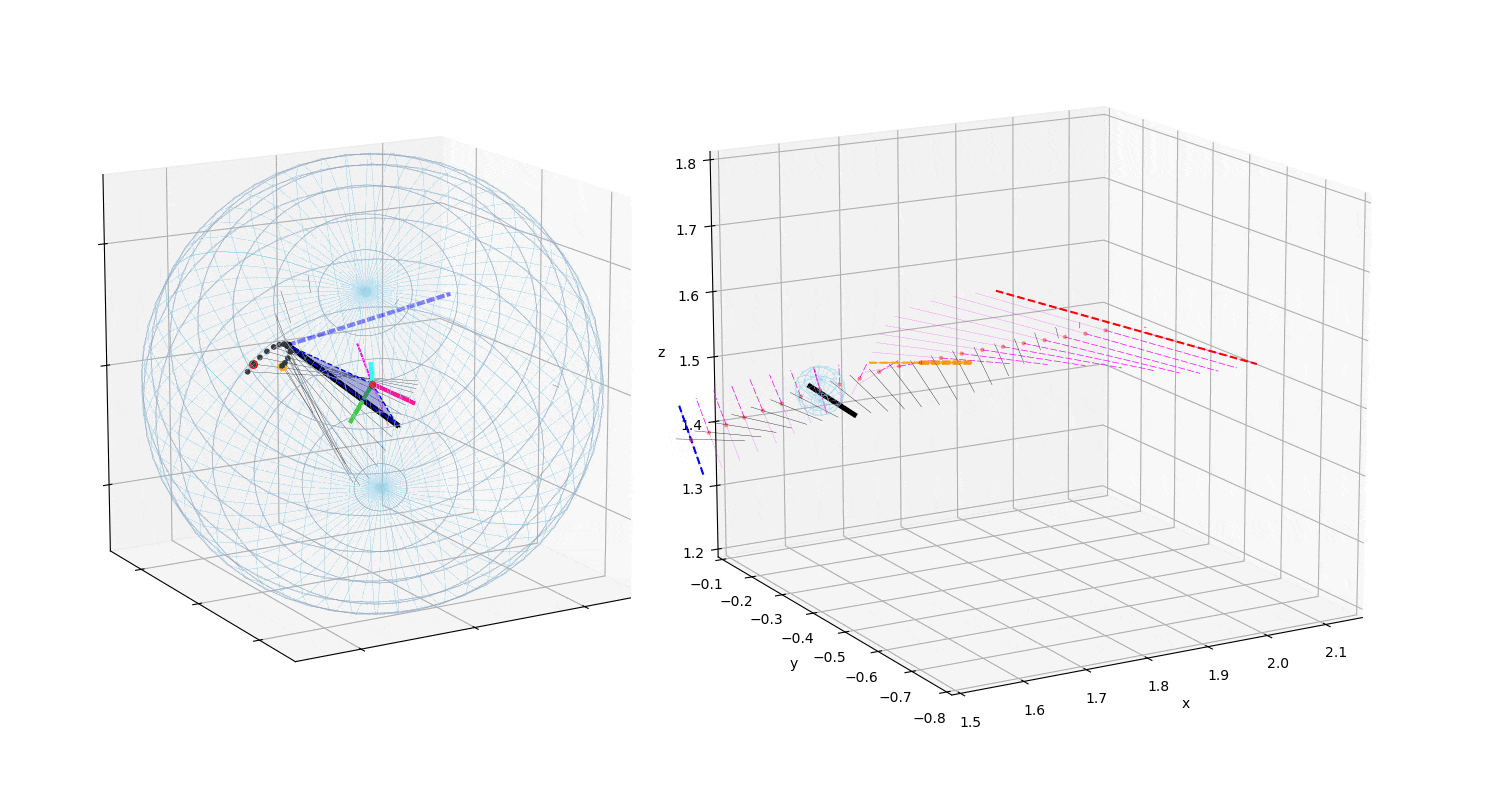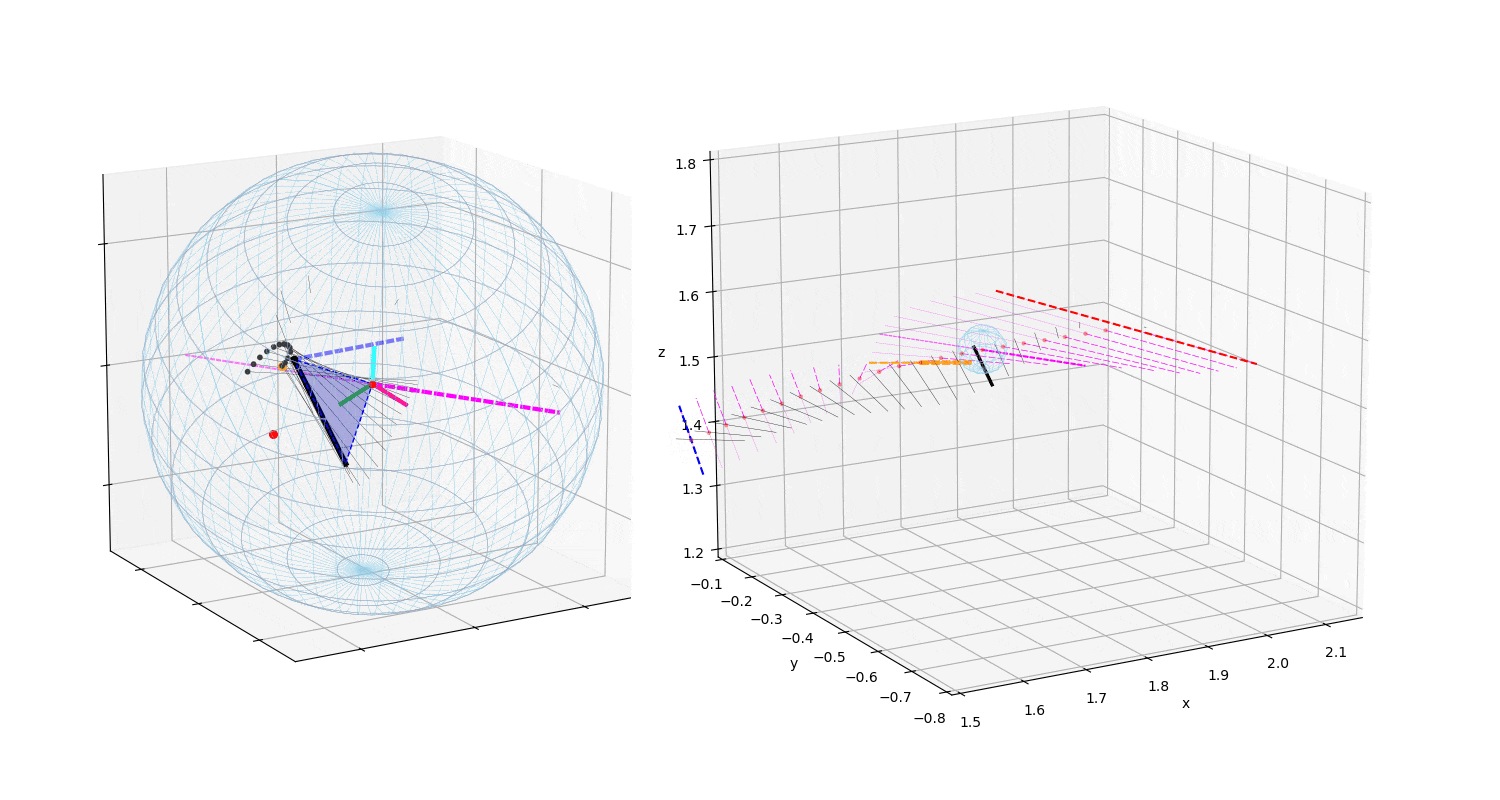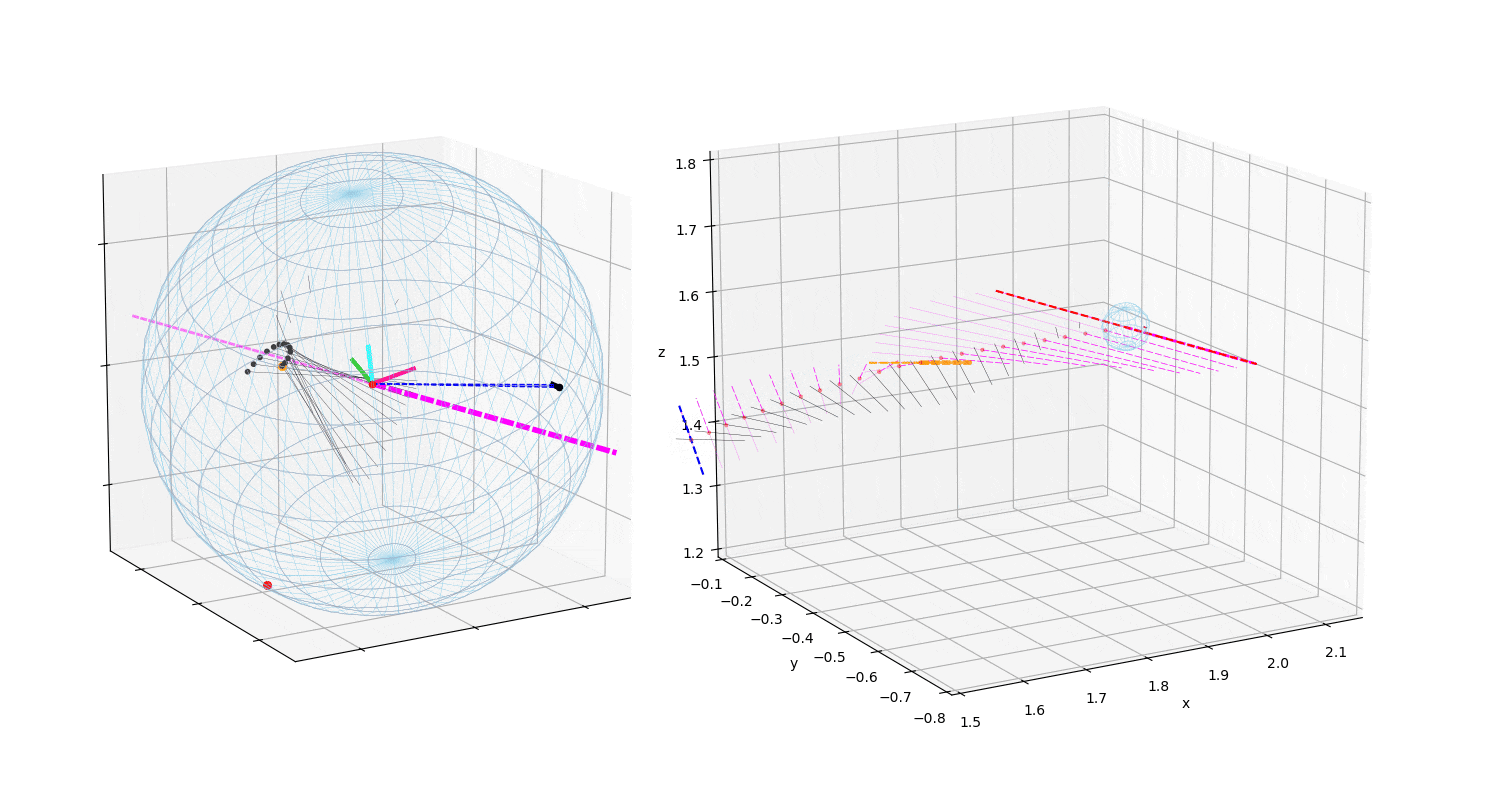
動画1:投球1
動画は回転制御フェーズ(BSモーメント発生〜BS開始〜リリース)のボールに作用する
力ベクトルの変化の様子を示す.Topは真上から見た図で投球方向は下から上方向,
Sideは真横(1塁側)から見た図で投球方向は右方向,Backは真後ろ(投手視点)
から見た図で投球方向は正面方向である.
マジェンタ色の破線は角速度ベクトルで,太い方向が右ネジ方向である.
黒太線がボールに作用する力ベクトル,その始点が力の作用点.青線がBSモーメント発生,
黄色い線がバックスピン開始を示す.
薄青の破線は投球方向に作用する力.ボールに固定した座標系を中心にRGBの色の線で示した.
「力の作用点–ボールの中心–力ベクトルの先端」を結んだ三角形の面積が,画面に垂直な方向を
軸とする力のモーメントの大きさを示す.
赤点は,BS開始の力の作用点の位置が,ボール表面を移動している様子を示す.
ボールに地球の相当する緯度線と経度線を描き,座標系の各軸をRGBの線で示した.
次の図7も参照.

図7:動画の補足説明図
回転制御フェーズにおけるボールに作用する力の作用点(接触点と考えて良い,力ベクトルの始点)は,動画のようにボールのどの方向から観察しても,ほぼ一定の位置にとどまっている.この間ボールは回転しているので,ボールは示指や中指の先端あたりで転がっている(補足2).このとき,指先からボールを観察すると(ボールの座標系から見た力の作用点は)約3cm移動している.いまのところ,その力の作用点がシームに対してどのように移動しているかはわからないが,ストレートの場合,示指や中指の指先あたりでボールを転がしているので「同じ指の位置で,またはシームを常に押しているわけではない」ことを意味している.また,それは面接触で,接触している領域はおおよそ1箇所にまとまっている.
回転力を増加させるために,回転力を与える接触点の移動距離や時間を長くすることには限界があるが,深く握ることでそれらを多少長くすることができるかもしれない.また,それ以外にも押す力を増大させるなどの戦略が考えられるが,検証が必要だ.
力の作用点と回転

図8:力ベクトルがつくる回転力(モーメント)
複数の指によるピンチング(把持)ではなく,ストレートのように一箇所に力を集中させるとき,ボールに作用する力ベクトルとボール中心とで構成される三角形の面に対して垂直な方向(法線方向)の軸まわりの回転力がほぼ支配的となる(図8).
動画2:投球2
133km/hの異なる投球の力の作用点と角速度ベクトルの変化
動画3:投球3
132km/hの異なる投球の力の作用点と角速度ベクトルの変化
投球2(動画2)や投球3(動画3)のTop(真上)からみた図を,投球1(動画1)と比較すると,力の作用点はボール中心の真後に近い位置に存在する.このため投球2,3の回転軸(マジェンタ破線)は真横(左右方向)に近い.すなわち上下方向の変化量を引き起こす回転成分を有効に利用している.
動画4:投手の斜め右後方からみた力ベクトルと角速度ベクトルの変化(投球1)
ボールの中心に固定された座標系(左)と絶対座標系からみた図(右)
動画5:投手の斜め右後方からみた力ベクトルと角速度ベクトルの変化(投球2)
ボールの中心に固定された座標系(左)と絶対座標系からみた図(右)
動画6:投手の斜め右後方からみた力ベクトルと角速度ベクトルの変化(投球3)
ボールの中心に固定された座標系(左)と絶対座標系からみた図(右)
投球1と2,3を比較すると,投球1(動画1,4)では角速度ベクトルは水平だが,前後方向に傾きジャイロ(回転軸の前後)成分の多い投球である.これは,ボールを押している位置(力の作用点)と力ベクトルの方向が影響している.投球2,3の力の作用点は投手の視線(Top,Back view)でボールの中央付近に近いところを下方に押しているのに対して,投球1ではやや右後方から斜めに押しているため,ジャイロ成分の多い投球となっている.
また,投球2(動画2,5),投球3(動画3,6)は,投球1(動画1,4)と比較し角速度ベクトルの大きさ(ベクトルの長さ)は少し小さいが,投手から見て左右方向の成分が大きく,結果,投球1と比較し上下の変化量の多い投球である.また下向きの力成分が大きい投球である.
なお,力の作用点は絶対座標系であまり移動しないが,小さいベル型の軌道を描いており,投球2や3ではやや大きめのベル型の軌跡を描く.
ここでは,3つの投球の回転軸と力の作用点の示したが,力の作用点などの違いが回転軸などに与える影響や,そのメカニズムやこれ以外のデータも含めて,制御の詳細について,またどこかで述べたい.
角速度ベクトルによるリリース後の回転量の評価
Rapsodoなどのスピン軸の水平軸の長さの比で計算する方法と異なり,ここではspin efficiencyを角度ベースの定義で示す.Top View(真上)やBack View(真後)の2つで定義し,スピンの効果量を分解する(図9参照).真上と真後からみた2つの角度で定義することで,スピンの特徴がより明確になるだろう.

図9:スピンの効率を真上と真横からみた成分に分解.
回転軸の傾き角度と角度ベースの効率を計算

図10:スピンのxyz成分.特にy,z軸成分が上下左右の実質的なスピンの効果を反映.
spin angle $\alpha, \beta$:水平軸と左右軸に対する角度.top viewとside viewのそれぞれの角度をそれぞれ$\alpha, \beta$とする.具体的な角度でスピンの効率を判断する指標である(図9参照).
spin angle efficiency $\eta_{\alpha}, \eta_{\beta}$:90degに対する割合で計算(真横に近いと100%).top viewの効率を$\eta_{\alpha}$,back viewの効率を$\eta_{\beta}$とする.spin angleをもとに真横が最も効率良いと考えた場合の,割合で示す指標である(図9参照).
effective spin:0.01$\times$ (spin angle efficiency)$\times$ (spin rate).角速度の大きさ$\times$上記の割合
spin rate component $\omega_x, \omega_y, \omega_z$:角速度ベクトルの各軸成分.$\omega_x$:投球方向成分,ジャイロ成分.$\omega_y$:左右方向成分.$\omega_z$:上下方向成分(図10参照).一般には,ストレートとカーブのようなスピンの球種の場合は$\omega_y$成分が,スイーパーのようなサイドスピンの球種では$\omega_z$が大きいほど変化量が大きいと考えればよいだろう.恐らくRapsodoのtrue spinと同義である.
なお,図9の角度ベースで効率を計算することは,三角関数ベースよりも厳しく評価することになるが,ボールの移動量の実質的な評価から乖離する.図10の角速度の成分で評価する方法はそれを補っている.
この定義で,先に示した投球1(図1,4),投球2(図2,5),投球3(図3,6)のスピンの特徴を示す,
表1:各投球のスピン量の特徴量
| 投球1 | 投球2 | 投球3 | ||
|---|---|---|---|---|
| 球速 | [km/h] | 130 | 133 | 132 |
| 角速度の大きさ | $|\boldsymbol{\omega}|$ [rpm] | 1938 | 2098 | 1675 |
| spin angle | $\alpha$ [deg] | 49.0 | 7.4 | 22.4 |
| spin angle | $\beta$ [deg] | -19.3 | -24.7 | -25.1 |
| spin angle efficiency | $\eta_\alpha$ [%] | 45.6 | 91.8 | 75.1 |
| spin angle efficiency | $\eta_\beta$ [%] | 78.5 | 72.6 | 72.1 |
| effective spin | $.01 \eta_\alpha |\boldsymbol{\omega}|$ [rpm] | 883 | 1925 | 1257 |
| effective spin | $.01 \eta_\beta |\boldsymbol{\omega}|$ [rpm] | 1522 | 1522 | 1207 |
| spin rate components | $\omega_x$ [rpm] | 1446 | 213 | 613 |
| spin rate components | $\omega_y$ [rpm] | -1220 | -1850 | -1449 |
| spin rate components | $\omega_z$ [rpm] | -415 | -845 | -698 |
投球1,2,3の例を比較すると,同程度の回転数(角速度の大きさ)であっても,回転軸(角速度ベクトルの方向)の向きの違いから,ボールの移動をもたらす実質的な効果はかなり異なる.
ストレートの特徴
ストレートの力学的特徴は転がりに代表される.
運動の自然さ
ストレートは,ある意味もっとも「自然な」投球である.その自然さは運動連鎖によって生じるバックスピンの回転に象徴される(投球の力学メカニズム(2) −バックスピンは運動連鎖−を参照されたい).たとえば反対にボールを無回転で投げようとすると,それが至難の業であることは直感的に理解できるだろう.ボールの中心に向かって力を作用させることができれば,ボールに回転力(モーメント)を与えないことができる.しかし,ストレートのようにボールを把持せず投げる場合は,無回転の投球はかなり難しい.なぜなら,ボールはわずかに力が中心方向からそれるだけで,簡単にボールが回転してしまう性質があるからだ.
しかし,普通のキャッチボールの投球の場合,回転のことを気にせず投げれば,目的の方向にボールを投げられる.投球方向に作用する力成分だけがボールを加速してくれるので,その力を増やすようにだけ制御すればよい.ボールには向心力も作用するが,それは回転を維持するための力で,手に自然に作用する力である.そして,そのように制御していれば,中心から外れた成分がボールに回転運動を与えるが,その回転運動は特にボールのコントロールには影響を与えない「自然に」発生するだけの都合の良い回転である.
また,その回転方向は通常バックスピンとなる力学が作用することはすでに述べた.つまり,ボールの回転開始がリリースを促し,投球方向の加速の減少がトリガーとなる.この結果,ボールに作用する力は変化球を投げようと制御しない限り必ず下向きとなり,必ずバックスピンの回転を起こす.ストレートでは,バックスピンは必ず発生する運動と考えるのがよい.
ストレートが自然な投げ方とすると,それ以外の変化球は多少,多少無理で不自然な投げ方をする特異的な投球とも言えるが,打者にさとられないように,回転軸や回転量をここまで制御できるのかという超絶技巧とも言えよう.
回転の制御
ストレートの特徴は「球速」と「バックスピンの回転数」の両方を増加させることを可能とする球種で,それはボールの転がり制御で可能とする.ボールに作用する力を中心より少し下向きにすることで,ボールの加速成分と回転させる成分を与えられる.

図11:(a) 力の作用点が中心を通る破線(y=0)に近く,力の前後方向(y)成分が大きいほど,
角速度ベクトルが真横を向く(ωy成分が大)
(b) 力作用点が右にそれると,回転軸(角速度ベクトルの方向)が傾く.
一般に,ストレートの場合,特に上下の変化量を生成する左右方向($y$方向)の軸まわり回転数の多い投球がよいとされる.そのような回転方向を生み出すためには,投球2,3の動画2,3に示したように,投球の後方($-x$軸方向)から見て,ボールの中心($y=0$)近くの位置に力の作用点が位置し,前方($+x$方向)に大きな力成分を保つ必要がある(図11参照).
また,回転数自体を大きくするためには,ボールのピンチングの力を増やすことや,回内や内旋運動を増やすことが重要とされているが,今後検証していきたい.
握りの重要性

図12:示指と中指間の力の作用点の移動
ストレートは転がりと述べているが,動画4,5,6の力の作用点の推移を観察するとわかるが,その軌跡は小さい「ベル型」の曲線となる.これは,恐らく力の作用点が示指と中指間で移動し,特に投球2,3では回転制御フェーズで中指から示指に移動し,投球1では反対に示指から中指に移動している.また,このことが投球2,3の回転軸の向きが真横($\omega_y$が優勢)を向いている理由と考えられる.また,実際,投球2,3の示指と中指の間隔は広く,大きな左右の軌跡の移動量を裏付けている.指の位置はこれらに加えて作用点は上下の運動を行っており,結果,ベル型の軌跡となるが,この上下運動のメカニズムは今後検証していきたい.なお,この事実は,少なくとも横方向では精密に作用点の移動を計測していることを示していると考えている.
ここでは,示指と中指の位置に注目したが,母指側の位置や方向なども重要である(最近は母指を曲げてシームに添える方法も選択肢の一つらしい).
当たり前だが,このことは握り方が,ボールの制御に大きな影響を与えていることを示唆している.回転制御フェーズは短い時間で終わるので,事前の準備が重要である.
おわりに
Rapsodoの登場で,ボールのリリース後の回転の挙動は,多くの人が比較的容易に計測できるようになった(補足3).しかし,回転の挙動を定めるのはリリース前のボールと手間の力学で,ボールの回転制御メカニズム(補足4)を理解するためには,リリース前のボールの力学挙動を調べる必要がある.そして,その理解に基づき,投手に重要な情報を投球直後にフィードバックし介入するトレーニングができれば,変化球や投球技術の習得に役立つかれない.まだ課題が多いが,ここで述べる情報を投球直後にフィードバックする環境が実験室レベルだが整いつつある.
また,ボールに慣性センサを組み込むことで,力とトルクを計測することができるが,恐らく正確に力の作用点を示した例は他にない(補足5).
これまで,スピンの挙動を示す基本的なメカニズムは明らかにしたつもりだが,まだまだ理解できていない細かい象も多い.例えば,転がりの位置が変化しないことは,安定した制球に繋がり,作用点の移動が反対に「抜け」という現象とにつながるのかもしれないが,さらなる数理的な理解が必要だ.
これまで,握り方や投げ方の指南が,経験や統計,または力学による推論から述べられてきた.それらの多くは,このボールの力学解析によって根拠を与えることができる.今後,投球のメカニズムの詳細が次第に明らかになってくるだろう(補足6).
補足
補足1:
投球の力学の基礎(1)でも説明したが,ボールに作用する力は,投球方向に作用する力と向心力に分解できると述べた.しかし,このことはあまり力学の教科書には出てこない分解の仕方なので少し補足する.
物体に作用する力を記述する際,いろいろな座標系の取り方が存在する.たとえば,図5,6のグラフは絶対座標系で表したデータである.ただし,代表的な絶対座標系も原点や方向の定め方で,力の成分は異なる.
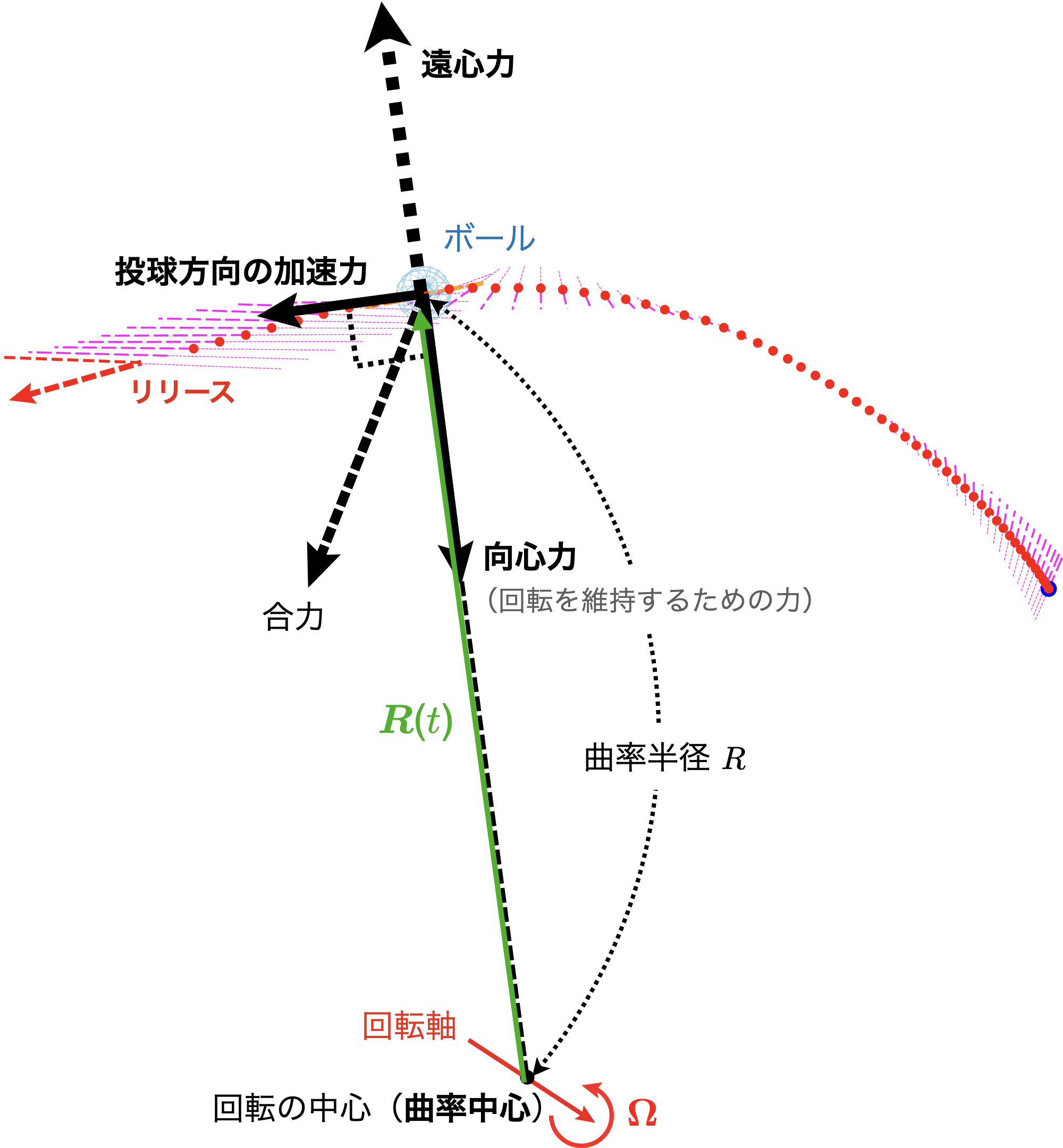
図13:曲率中心を原点とする極座標系からみた,ボールに作用する力
ボールの重心の運動を「一つの回転運動」だけで記述することができるが,その回転の中心を曲率中心と呼ぶ.そして,ここでは曲率中心を原点とする座標系も採用している.この座標系の原点である曲率中心は,等速回転運動(半径と回転速度が一定)を行っていない限り運動中,移動することに留意されたい.曲率中心からボールまでの長さを曲率半径$R$と呼ぶ.なお,曲率$\kappa$は半径$R$の逆数$\kappa=1/R$である(図13).
ボールの重心の運動を,曲率中心を原点とする座標系で考えると,「ボールには」曲率中心に向かう向心力が作用する.向心力は遠心力の力の反作用の力である.遠心力は「ヒトに」作用する力で,ボールがヒトを外側に引張る力である.単に見ている立場で異なるだけだ.
向心力は見かけの力などとも呼ばれるが,重要なことは円運動を行っているときに作用する力で,実際にボールに作用しているので誤解しないでいただきたい.
曲率中心からボールまでの位置ベクトルを$\boldsymbol{R}$としよう.また,曲率中心から見たボールの中心点の運動の角速度ベクトルをここで,$\boldsymbol{\Omega}$としよう.この$\boldsymbol{\Omega}$は,ボールを剛体としてみた角速度ベクトル$\boldsymbol{\omega}$ではなく,曲率中心まわりのボールの進行方向の運動を記述する角速度ベクトルであるので注意をされたい.するとボールの速度ベクトルは
$$
\boldsymbol{v} = \boldsymbol{\Omega} \times \boldsymbol{R}
$$
と記述される.このような座標系の取り方を行うと,曲率中心は移動するにもかかわらず,式に並進運動の成分は現れない.つまり,曲率中心を計算できると,一つの回転運動で記述することができる.ただし,投球方向の力を計算するだけなら,ボールの接線方向に作用する力成分を計算すればよいので,曲率中心を定める必要はない.
なお,角速度ベクトル$\boldsymbol{\Omega}$には,半径の軸$\boldsymbol{R}$方向の成分は含まないことにも注意されたい.
これは一般に極座標系と呼ばれる座標系だが,移動する曲率中心を原点とする極座標系で,力学の教科書には恐らく出てこない少し特別な座標系である.
さて,向心力の意味をもう少し考える.ここから妄想になるが,移動する曲率中心からボールまで伸びる糸を考え,ボールが回転運動をすることを考える.ただし,糸の長さ$R(t)$は時々刻々変化し($t$は時間で,$R$は時間の関数という意味),伸縮する.対象とする運動は糸で繋がれたボールの回転運動だが,これをボールと糸から構成される振り子と考え,ここで,これを可変長振子と呼ぶ.
可変長振子であるボールには回転の中心である曲率中心に向かう向心力が作用する.残りはボールを加速する投球方向の力だけとなる.つまり,ボールには「投球方向に作用する力」と「向心力」に分解できる.繰り返しになるが向心力は回転を維持するための力なので,糸が切れるとボールは投球方向(接線方向)に飛んで行くだけである.向心力はボールに作用するが,回転を維持するための自然発生的な力で,投手の立場からすると,投球方向に投げようと力を制御すればよいだけで,加速するために向心力を増やそうなどと下手に考えないほうがよい.
補足2:
リリース前の力の作用点は,少し上方向へ移動しているのは,力の作用点を計算する際に,角速度やトルクの誤差と小さな力で割り算を行っていることによる計算誤差と考えて良い.
補足3:
我々の方法は比較的正確な計測方法だが,RapsodoやTrackmanも基本的には1方向からの計測なので精度の低い方向が存在する.Rapsodoなどの計測器がどの程度正確かはまだ確認していないが,そのうち行う予定である.
補足4:
バイオメカニクスにおける,多くのメカニズムは力学現象の幾何学的(ベクトル的)な理解が重要だ.統計や機械学習やデータを見比べてもわからないことが多いだろう.
補足5:
Fussらは,IMUを組み込んだクリケットボールでCOPを計測し,COPは力の作用点と同一と述べているが,それらは別物である.そもそも曲面に作用するCOPを定義できないだろう.
補足6:
ボールの投げ方を最も拘束するのはヒトとボールの力学的構造である.例えば,ここで述べたようにボールに作用する力が最大値となることが,ボールのリリースのトリガーとなる.しかし,このような拘束は多様な投げ方の一部を拘束するが,その拘束が許す回転制御の自由度は大きいので,投手のアイデア次第で多様な投げ方が可能である.一方で,力学的理解が進み,強化学習などによって科学の力で新しい球種が開発されることもあるかもしれないが,現状,そこまで研究は進んでいない.現状の科学やデータサイエンスは,ヒトが行う行動の後追いであって,特に平均的な行動の後追いである.ヒトの創造性ははるかにそれを上回っている.データサイエンスなどに基づくMLBの野球がつまらなくなってきたという話に筆者は共感する.科学の重要性を否定するつもりは全くないが,スポーツ科学は,ひどい誤りも多いし,まだまだ狭い世界を見ているのではないだろうか.
ひとつだけ加えておくと,現在のデータサイエンスと,物理には大きな違いがある.物理は理(ことわり)を探求する学問で,その探求が進めば予測から創造へとつながる余地がある.つまり新しい投球方法を開発する道具として機能する可能性は十分にある.しかし現状,機械学習は理を学習することはない.分析とか解析とか狭いところを見るのではなく,予測や創造を可能とする俯瞰できる理の理解が求められていると筆者は考える.