はじめに
大リーグ(MLB: Major League Baseball)はStatcastというデータのトラッキングシステムを通して,全試合のデータを公開していることを多くの方はご存知でしょう.このため,データサイエンス(統計や機械学習)の観点から多くのMLBのデータの分析がなされています.分析方法などはそれらの先駆的な方々から学ぶのが良いと思います.
公開されているデータには,力学分析に関連する項目は少なく限られていますので,できることも僅かですが,単にグラフ描くのではなく,そこから「背後にある物理ルール」,つまり「メカニズム」を考えてデータを眺めることが今回の記事の狙いです.
また,データを統計や機械学習だけの観点から分析し理解できることは限られ,その物理現象を支配する力学拘束などの「先行理解なしの理解は困難」というのが筆者の考え方です.ただしここで行っている分析は簡単な統計です.
この記事では解析したPythonコードも念の為,示しました.コードの大半はAIが指南しているので,解析に使用したコードはひどくないでしょうが,エンジニアが見ると素人と思う部分もあるかと思いますが,その場合はお許しください.あくまでも力学の観点の記事です.
Pythonなどを利用すれば,誰でも簡単にMLBのデータを入手できます.Pythonも動かすだけなら,簡単です.力学はともかく,自分でグラフを描いてみたいという方も,下記の「Google Colabでお試し」で動かしてみるとよいでしょう.わからないことは,AIに聞けば教えてくれます.
球速と回転数:比例と反比例の両立
結果を示すのが少し先になりますので,先に結論を述べておきます.
ストレート(4-seam fastball)の球速と回転数の間には,「比例」と「反比例」の矛盾する両方の性質を持ちます.
ボールを加速する運動として身体全体の回転運動を考えると,その身体全体の角速度という変数に対し,球速と回転数の両方とも増加するため球速と回転数はラフに比例します.球速の異なる投手が投球すると,または同じ投手が球速を変化させて投球すると,それに応じてボールの回転数も増加します.
一方,「ボールに与える力を一定とする拘束」を与えると,たとえば力の作用点のちらばりに応じて,球速と回転数の割合が変化します.たとえば同じ投手が投げる場合は,ボールに与える力の大きさにさほど違いがないと考えると,力の作用点が少しずれることで,球速と回転数のどちらかに重みが偏ります.投手が異なると戦略も異なり,その重みが異なってきます.この性質により,球速と回転数が反比例する特徴も統計的に現れます.
ここでは,そのメカニズムについて考えていきます.
Python環境について
エンジニアの方,アナリストの方はここを読み飛ばしてください.
使用するのはPythonですが,筆者はプログラミングやアナリストとしては素人ですので,Pythonなどの説明を私が行うのはやめておきます.適切なPython環境はその人によってかなり異なり,素人がとやかく述べてもと考えています.
もし,それでもPython環境の構築のヒントが必要でしたら,素人のコメントですが以下にまとめました.
1.Python環境を導入するのが大変と思う方,今後Pythonを使用するかわからない方は,Google Colabなどを利用すると良いでしょう.クラウドで計算してくれます.
Google Colabについては,せあぶらさんの記事や,バイオメカニクスにご興味がある方は昔に前職で書いたnote記事も役立つかもしれません.
筆者が書いた記事から,Google Colabもかなり変化しており,記事の内容が古くなっておりますが基本は同じです.
2.筆者の最近手離せない環境はCursorです.
これに普通にPythonをインストールし使用しています1 .Cursorの有料版も十分価値もあると感じます.他にも良い環境があるでしょうが,次にタイプすべき内容をAIが推測し,作業効率が格段にアップします.時として間違いますが,結構まともなコメントまでも作成してくれます.
3.そもそもPythonを学びたい方.エンジニアではなく,科学目線でプログラミングのPythonのことを学びたいなら,個人的には三谷先生の「Python ゼロからはじめるプログラミング」
が好きです.しかし,大きな本屋に行くことができるなら,ひとつひとつ手にとって自分に馴染む本を選ぶとよいでしょう.
とにかく動かすということであれば,野球データでやさしく学べるPython入門という書籍もあります.
Google Colabでお試し
手っ取り早く動かしたい方は,下記のリンクで試しください.コードのコピペも不要で,すぐに実行できます.ただし,Googleでのログインが必要です.
MLBデータの入手
Python環境が構築されているという前提で,以下,話を進めます.
MLBのデータの入手方法は,せあぶらさんの記事の記事などを参照していただければと思います.
Python環境が構築して,まずMLBのデータ(ここではStatcast)を取り込むためのライブラリをインストールします.
!pip install pybaseball
または,jupyter環境なら
pip install pybaseball
を実行します.
pybaseballはMLBのStatdataを含むデータサイトからデータを取得するライブラリです.通常のPython環境には,このようなライブラリはPython環境には含まれないので,このインストールが1度だけ必要となります.
以下のように,必要なライブラリを呼び込みます.
# Code 1
from pybaseball import statcast_pitcher
from pybaseball.playerid_lookup import playerid_lookup
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np
import os
pybaseball以外でも,たとえばsklearnなどがインストールされていない場合は,エラーが出ますので,その場合は,
pip install sklearn
または
!pip install sklearn
などのように,不足しているライブラリを適宜インストールしてください.
対象選手
取得対象の日本人投手は以下の選手としました.ただし,ダルビッシュ投手は2024年の,大谷投手は2023年のデータを使用します.他の選手は,今年のデータです.
players = {
"Yamamoto": ("Yoshinobu", "2025"),
"Sasaki": ("Roki", "2025"),
"Imanaga": ("Shota", "2025"),
"Senga": ("Kodai", "2025"),
"Matsui": ("Yuki", "2025"),
"Sugano": ("Tomoyuki", "2025"),
"Kikuchi": ("Yusei", "2025"),
"Darvish": ("Yu", "2024"), # 2024
"Ohtani": ("Shohei", "2023"), # 2023
}
データ取得と前処理
全選手のデータをダウンロードするとかなり時間がかかります.一度取得したデータは保存し,データが保存されている場合は,それを再利用すると良いでしょう.
ここでは,対象とする選手だけデータを取得することとします.この場合,データのダウンロードにかかる時間は比較的短いです.
下記コードでは,各個人のデータは上記の選手だけ取り込み,Statcastの全データ項目をcsvファルに保存します.そのうち,
'release_speed', 'release_spin_rate', 'plate_x', 'plate_z',
'release_pos_x', 'release_pos_z', 'arm_angle', 'spin_axis',
'vx0', 'vy0', 'vz0', 'p_throws'
だけをここで,使用します.
これらは,
リリース速度(mph),回転数(rpm),ホームプレート上の投球位置x(左右 feet),ホームプレート上の投球位置z(上下 feet)
リリース位置のx(左右 feet),リリース位置のz(上下 feet),腕の角度(deg),スピン軸の角度(deg)
リリース時の速度x(mph),リリース時の速度y(mph),リリース時の速度z(mph),投球に使用する腕(左右 'L' or 'R')
を示しています.この章では'release_speed', 'release_spin_rate'だけ利用します.他の項目は,別の記事で利用する予定です.
詳細は,
Statcastで取得しているデータの定義(英語)をご参照ください.
ここでは,これらのデータをDataFrame(df)という二次元の表形式のデータ(テーブルデータ)に格納しますが,それを利用するためのPandasというライブラリも必要になります.DataFrameについては,nkmkの記事などをご覧になるとよいでしょう.個人的にはPandasの利用は苦手で,行列やベクトル的なnumpyという配列に置き換えるほうが好きなのですが,ここではChatGPTが示した例に従います.
なお,以下のコードでは
・4 seam fastball(ストレート)
・1800 rpm以上の回転の投球
を抽出し,単位はfeetからmに,MPH (mile/hour)からKMH (km/hour)に変換しています.
次のCode 2をご覧になるとわかりますが,計算はDataFrameを使用する際,たとえば
MPH_TO_KMH = 1.60934
df['release_speed'] = df['release_speed'] * MPH_TO_KMH
のように,df['項目'] を変数のように扱い,計算を行うことができます.
また,別の処理の都合で,左投手の'plate_x'と'release_pos_x'の左右の位置を入れ替えて(符号を反転して)います.また,NANデータも"dropna()"関数で除去しています.
# Code 2
# データを保存するディレクトリの確認と作成
data_dir = "statcast_data"
if not os.path.exists(data_dir):
os.makedirs(data_dir)
# 対象選手(First Name, Year)
players = {
"Yamamoto": ("Yoshinobu", "2025"),
"Sasaki": ("Roki", "2025"),
"Imanaga": ("Shota", "2025"),
"Senga": ("Kodai", "2025"),
"Matsui": ("Yuki", "2025"),
"Sugano": ("Tomoyuki", "2025"),
"Kikuchi": ("Yusei", "2025"),
"Darvish": ("Yu", "2024"), # 2024年データ
"Ohtani": ("Shohei", "2023"), # 2023年データ
}
# データ格納
all_data = pd.DataFrame()
# 各選手のデータ取得(2023〜2025)
for last_name, (first_name, year) in players.items():
file_path = os.path.join(data_dir, f"{last_name}_{year}.csv")
# ファイルが存在する場合はロード、なければダウンロード
if os.path.exists(file_path):
print(f"Loading {last_name} ({year}) from file")
df = pd.read_csv(file_path)
else:
try:
pid = playerid_lookup(last_name.replace("_2023", ""), first_name).iloc[0]["key_mlbam"]
print(f"Fetching {last_name} ({year}) - ID: {pid}")
df = statcast_pitcher(f"{year}-01-01", f"{year}-12-31", pid)
# データを保存
df.to_csv(file_path, index=False)
except Exception as e:
print(f"Error with {last_name}: {e}")
continue
# データの加工
df = df[df["pitch_type"] == "FF"] # fastballだけを選択
df = df[df["release_spin_rate"] > 1800] # 1800rpm以上の回転数
df = df[['release_speed', 'release_spin_rate', 'plate_x', 'plate_z', 'release_pos_x', 'release_pos_z', 'arm_angle', 'spin_axis', 'vx0', 'vy0', 'vz0', 'p_throws']].dropna()
# 単位変換:mph → km/h, feet → m
MPH_TO_KMH = 1.60934
FEET_TO_M = 0.3048
df['release_speed'] = df['release_speed'] * MPH_TO_KMH
if df['p_throws'].iloc[0] == 'L':
df['plate_x'] = -df['plate_x']
df['release_pos_x'] = -df['release_pos_x']
df['vx0'] = -df['vx0']
df['vy0'] = -df['vy0']
df['vz0'] = -df['vz0']
df['plate_x'] = df['plate_x'] * FEET_TO_M
df['plate_z'] = df['plate_z'] * FEET_TO_M
df['release_pos_x'] = df['release_pos_x'] * FEET_TO_M
df['release_pos_z'] = df['release_pos_z'] * FEET_TO_M
df["player"] = last_name
all_data = pd.concat([all_data, df], ignore_index=True)
これで,もしこのコードが存在するディレクトリ(フォルダ)に"statcast_data"というフォルダがない場合は,"statcast_data"フォルダに各個人のデータを保存します.
"statcast_data"フォルダがある場合は,ダウンロードせず,一度保存したファイルからデータを読み込みます.新規にデータをstatcastからダウンロードする場合は,このフォルダごと消去してください.
球速と回転数の散布図とPCAと最小二乗回帰
球速と回転数の比例と反比例構造の両立
# Code 3
# プロット
plt.figure(figsize=(12, 8))
colors = plt.cm.get_cmap("tab10")
for i, player in enumerate(all_data["player"].unique()):
subset = all_data[all_data["player"] == player]
x = subset["release_speed"].values
y = subset["release_spin_rate"].values
plt.scatter(x, y, alpha=0.9, color=colors(i % 10), s=2.5) # , label=player
# 最小二乗法回帰
coeffs = np.polyfit(x, y, 1)
x_line = np.linspace(min(x), max(x), 100)
y_line = coeffs[0] * x_line + coeffs[1]
plt.plot(x_line, y_line, linestyle="--", color=colors(i % 10), linewidth=1.5)#, label=f"{player} LS")
# PCA回帰線
X = np.column_stack((x, y))
pca = PCA(n_components=2)
pca.fit(X)
center = X.mean(axis=0)
vec = pca.components_[0]
scale = 30
line_pca_x = center[0] + np.array([-5, 5]) * scale * vec[0]
line_pca_y = center[1] + np.array([-5, 5]) * scale * vec[1]
plt.plot(line_pca_x, line_pca_y, linestyle="-", color=colors(i % 10), linewidth=1.5, label=f"{player}")
plt.xlabel("Velocity (km/h)", fontsize=12)
plt.ylabel("Spin Rate (rpm)", fontsize=12)
plt.title("4-Seam Fastball: Spin Rate vs Velocity (>1800 rpm)", fontsize=14)
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
上記の# Code 1~3を実行すると,下記のようなグラフが描けると思います.
他の選手などを加筆するなど,各自変更を加えて実行してみてはいかがでしょうか(このファイルに変更は保存されないで,各自のColab環境にファイルをコピーして,修正をしてください).
図1:MLBの日本時投手のストレートの全投球の球速と回転数の散布図
「球速と回転数の関係に,比例と反比例の構造が混在する」ということは,一体どのようなことかと思われるでしょう.理由は,以下で少しずつ説明していくことになります.
ここでひとつだけ注目したいことがあります.たまたまかもしれませんが,回転数の大きな投手ほど,分散が比較的小さいということです.回転数を増やす投球は,自然さから(自然な投球から)離れる傾向にありますので,回転数を増やす制御をすることで分散も小さめになるのかもしれません.
なお大谷投手の散らばりが大きいのは,2023シーズン全体の統計という理由もあるかもしれませんのでご注意ください.
また千賀投手と大谷投手のPCAの傾きが少し異なります.これはまた異なる分析で現れる傾向で,またどこかで述べます.
MLBの全投球分布(2024と2025)
MLB全体の全投手の全投球の散布図はかなりの点で埋め尽くされますが,最小自乗回帰とPCAの傾きは日本人投手とほぼ同じです.2025年(オレンジ)は6月の途中までですので,サンプルは少なく,これからサンプル数増えると,2025年のように平均値(線が交差する点)から周辺に増えていきます.
つまり,相当な数が点で埋め尽くされていて,めったに投げられないような暴投などが周辺で目立っているのかもしれないことに注意してください.
図2:MLBの全投手のストレートの全投球の球速と回転数の散布図
ここに先程の日本人投手のグラフをラフに貼り付けたのが,下記の図です.日本人の9投手はおおよそ平均的なところを分布していることがわかります.
このぐらいの数のほうが,実際の分布をイメージしやすくなります.
図3:MLBの全投手と日本時投手のストレートの全投球の球速と回転数の散布図の重ね書き(図はラフに重ねているので注意)
図2を一見すると,なぜ最小二乗とPCAの傾きが10倍近く異なる理由がわかりません.しかし実際には図1のような分散の分布が理由でした2.
球速と回転数の間の力学構造
MLB全体でも,選手個人でも,ストレートの全投球の球速と回転数間の分布図の,最小自乗(二乗)とPCA(第一主成分の軸)の傾きは大きく異なります.線形近似するなら最小自乗(二乗)近似の直線となり,このことは平均的には「球速と回転数間に比例関係が存在する」ことを意味しています.
このことを,以前の記事投球の力学メカニズム(5) −スピン回転軸は向心力で定まる−で説明した可変長振子3を用いて説明するならば,
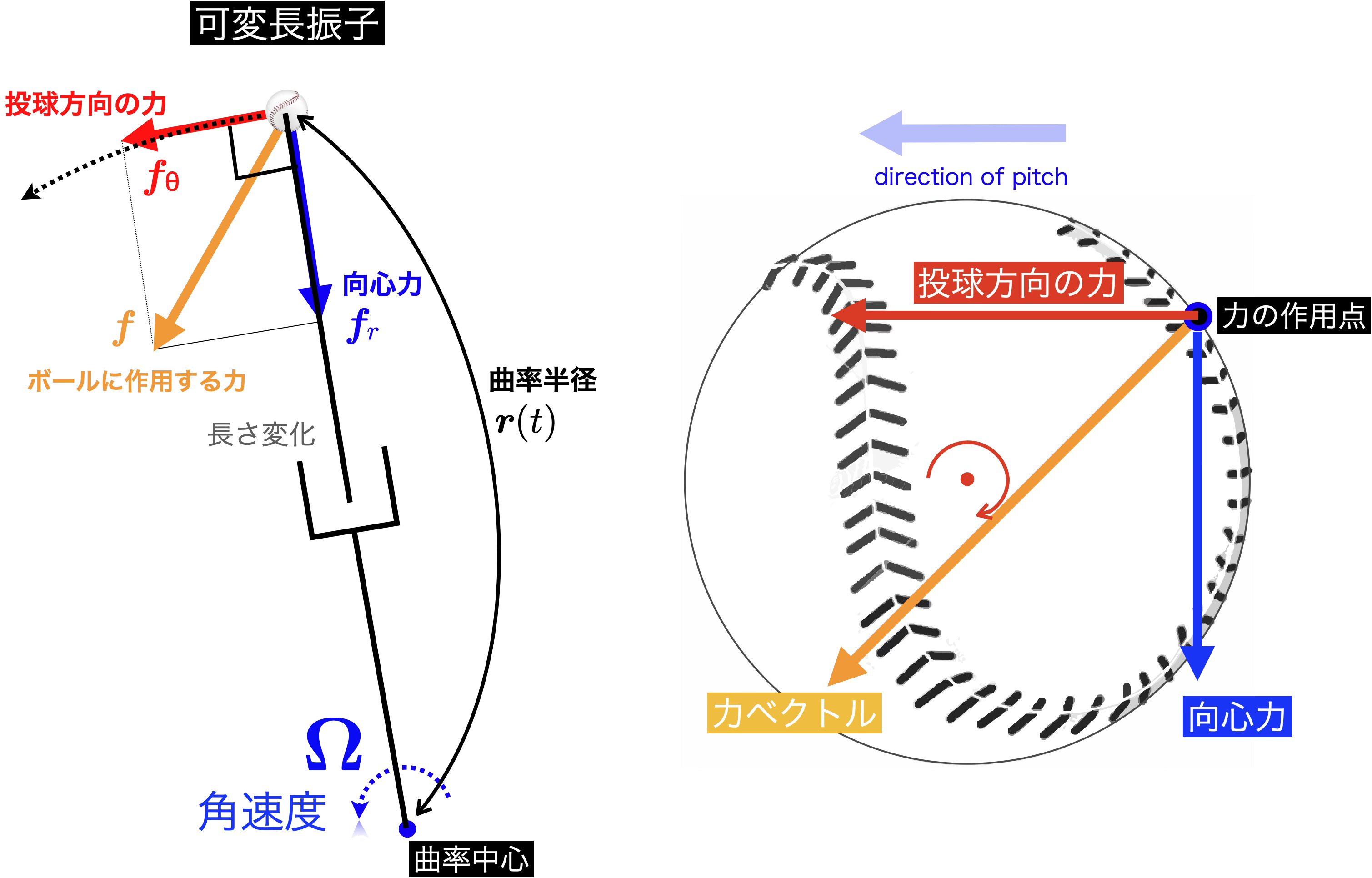
図4:可変長振子とボールに作用する力
ボールには互いに直交する,ボールの速度(投球)方向に作用する力と向心力とに分解でき(図4),投球方向に作用する力はボールの速度にそのまま寄与し,向心力は「おおよそ」ボールの回転力(バックスピンを生成する力)に寄与します.ボールの回転力(スピンを発生する力)はボール表面の接線方向に作用する力ですが,向心力は投球時におおよそ接線方向を向きます.
また,ボールのバックスピンの回転数に寄与する向心力はボールの運動軌道から計算される曲率中心方向を向き,その半径が曲率中心です.この曲率中心からボールまでを長さが変化する振り子と考え,ここでは可変長振子と呼びます.向心力の大きさ$|\boldsymbol{f}_r|$はこの可変長振子の半径である曲率半径$r$と振り子の角速度(回転速度)$\boldsymbol{\Omega}$の二乗に比例し
$$
|\boldsymbol{f}_r| = m r |\boldsymbol{\Omega}|^2
$$
となります.
また,ボールの速度ベクトル$\boldsymbol{v}$は
$$
\boldsymbol{v} = \boldsymbol{\Omega} \times \boldsymbol{r}
$$
となることから,球速も回転数も,可変長振子の角速度$\boldsymbol{\Omega}$に依存し,ストレートではバックスピンは必ず発生する自然な回転であることからも,球速と回転数はラフに比例関係があることを裏付けています.
ばらつきを説明する二つのストーリー
MLB全体,さらには日本の高校球児まで含めて,ありとあらゆる球速と回転数の散布図を描くと,図2の分布はおおよそ最小二乗方向に増えていきます.そこでここでは,「ボールに作用する合力(図4のオレンジ色の合力)が同じ大きさ」という拘束を与えることを考えます.つまり,おおよそ同じ球速や全力で投球する状況を考えます.よほどのときでない限り,100kmh程度のファストボールを投げることはないはずです.
力の向きの変化
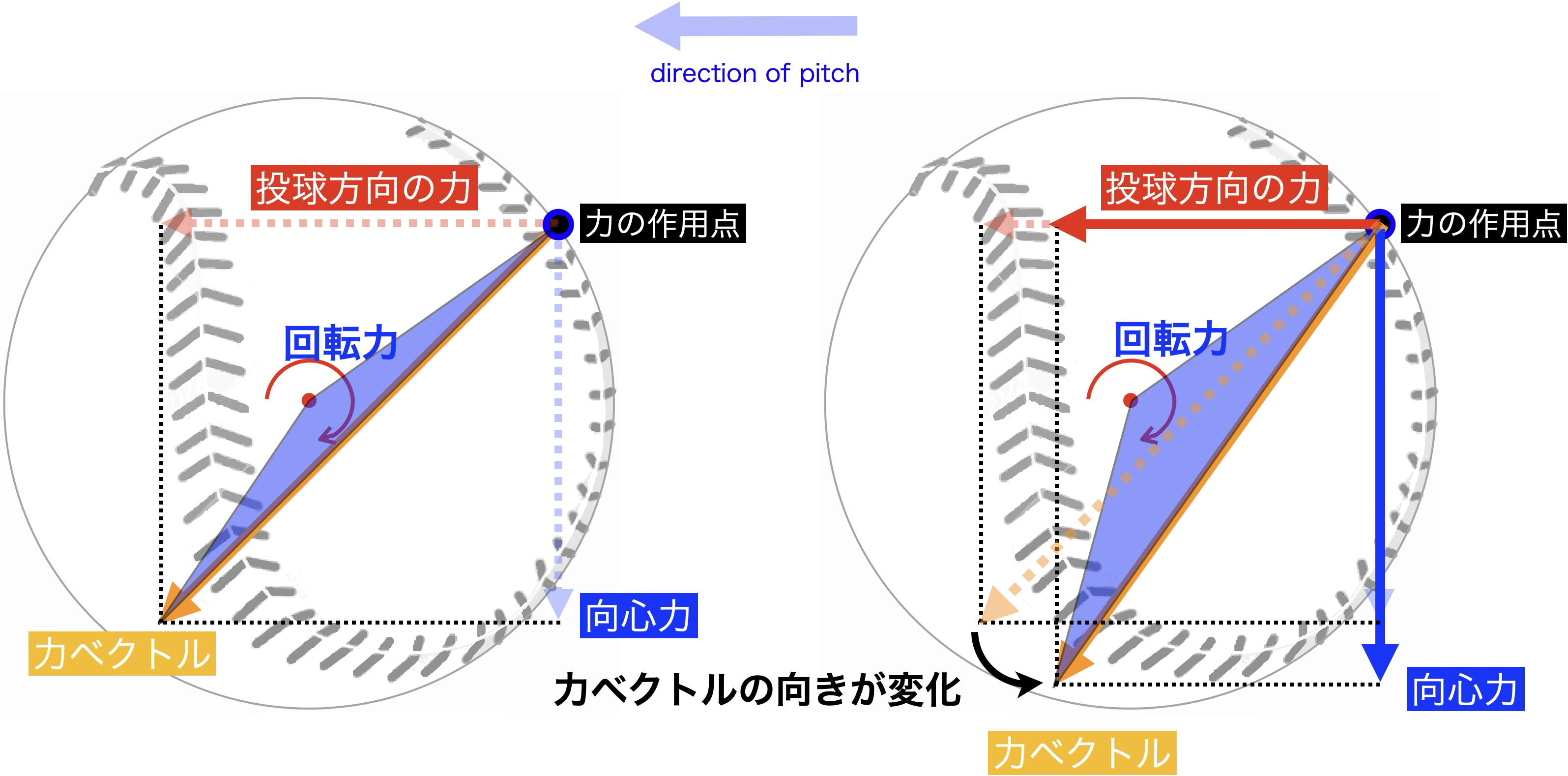
図5:力ベクトルの向きの変化による,投球方向の力と回転力の変化
そこで,「ボールに作用する合力(図4のオレンジ色の合力)が同じ大きさ」という拘束を与え,さらに,オレンジ色の合力ベクトルの方向が少し変化することを考えます.すると,球速と回転力の割合が少し変化し(図5),結果球速と回転数が変化することになります.このようなばらつきが発生するなら,球速と回転数間には反比例構造があることが推察され,PCAの分散や日本人投手9名の分布(図1)は,そのことを裏付けているかもしれません.
力の作用点(接触点)の位置の変化

図6:力の作用点の位置の変化による,回転力の変化
次にもう少し異なる状況を考えます.「ボールに作用する合力(図4のオレンジ色の合力)が同じ大きさ」という拘束は同じですが,力ベクトルの向きの変化ではなく,力の作用点の位置の変化を考えます.力の作用点が少し下に位置すると,投球方向の力に変化はあまりありませんが,回転力の大きさに影響を与えます.実際には,ストレートが転がり接触であることを考えると,力の作用点を変化させることは接触点(力の作用点)の位置を維持しづらいことが予想され,投球方向の力や回転力を減らす作用があるかもしれません.
なお,ボールに与える回転力(スピンを起こす力)は,この図では青色の三角形の面積で示しています.回転力は力のモーメントで,それはベクトルの外積の計算ですので,本来その大きさは平行四辺形の面積で表すべきですが,簡易的に三角形の面積で示しています.
このようなばらつきが,力の作用点,または力ベクトルの向きの変化のばらつきに依存するのかは,実際の実験データによる検証が必要となりますが,力の向きはその人の投げ方でかなり拘束されるので,筆者は後者(力作用点の変化)がばらつきの主な理由ではないかと考えています.
なお,図2のように全投手の分布を描くと数が多すぎて,このような反比例構造は見えにくいにですが,分散はこの反比例構造を裏付けています.もちろん図1の空白領域にも分布する選手が存在する可能性はあります.
個人間変動と個人内変動
データサイエンス的に図1のような分布は,個人間変動(interindividual variability)と個人内変動(intraindividual variability)が異なる構造を持つ例と考えることができるでしょう.
基本的に投手は,あまり球速を変化させることが少なく,おおよそ一定の速度で投げることが多いため,このような分布を示すと言えますが,力学的に球速と回転数は反比例する構造も存在し,このような比例と反比例の相矛盾する構造が両立します.統計はほとんど計算しないのでわかりませんが,ひょっとすると統計やデータサイエンス的に面白い例かもしれません.
おわりに
ここではストレートにおける球速と回転数の関係を,MLBのStatcastのデータを用いて検証しました.
筆者の専門は力学で,メカニズムに興味があります.ここで示してきたように,MLB全体のデータを眺めるだけでは,反比例構造はわからなかったかもしれません.まず「力学拘束を考え」,次に「日本人投手だけのグラフを描く」ことで,このような考察ができたということに注目してください.データの分析はこのような(特に力学的)先行的な理解なしに,理解しようとすることは難しいということを裏付ける一つになったかと思います.これは背後にあるルールが複雑であるほど,このようなことが発生します.
データサイエンスでは,多くの場合,Nを武器に機械学習や統計などいろいろな方法で分析が行われますが,先行的な理解とデータ解析の融合は重要です.この場合N=1でも理解できることも多いです.
またデータ解析から,複雑なルールを推測することは至難の業です.ここでは,図4のような力学構造(力の作用点)や,「可変長振子の角速度」を介すことで「球速」と「回転数」間の力学関係を理解したわけですが,データ分析だけは,せいぜい相関関係が理解できるだけで,比例と反比例的な関係が混在する理由を見つけることは,かなり困難でしょう.
「相関」で記述する「関係性」とは「風が吹けば桶屋が儲かる」程度のことしか言えないと理解するとよいでしょう.テンソル解析など複雑な解析を通せば,背後のブラックボックスがわかると期待する人もいますが,それは次元を増やすしただけで,それは複雑な構造を見つけることにはならず,所詮「関係性」で,因果関係も関係性の延長にすぎません.メカニズムとは多くの場合数理で記述できますが,単なる関数近似でもありません.
図4,5,6で示した力学関係を,速度と回転数の分析だけから読み取ることは,まずできないでしょう(10年後のAIはわかりませんが).
今回の分析からもうひとつ述べたかったことは,このようなばらつきが指の開閉のタイミング調整や,手先の動きで定まるものではなく,全身の力学が強く拘束し定まっていることです.このようなばらつきは投球に限った問題ではありません.今回の例は,単純にデータを分析するだけでなく,背後にある拘束を考えるきっかけになると幸いです.
我々の身体運動は,神経系(脳)が自由に運動を制御していると考えがちですが,みなさんが想像する以上にまず身体や道具の力学に拘束されており,その理解なしに神経系の理解は困難というのが筆者の主張です.さもないと何でも神経系の制御ルールの結果,このような運動を行っていると勘違いをしてしまいます.ボールのリリースが,指の開閉で定まると信じている人がいますが,これは力学条件の変化によって定まることは,まさにそのことを示しています.
次回もStatcastのデータを利用し,異なる力学視点で分析を試みる予定です.


