TL;DR
- k-meansは計算が軽く、stacking用の特徴量生成なんかでも使える。
- でもクラスタ数を決めるのが悩ましい。グリッドサーチ的なこともいいけど、どうやらクラスタ数を勝手に決めてくれるX-meansというものがあるらしいので試してみる。
- また、K-meansの可視化でちらほら見かけるボロノイ図のPythonでの描画の仕方について試してみる。
まえおき
統計とか数学とか機械学習とかの専門家ではないので、勘違いやミスなどあるかもしれませんがご容赦ください![]() (勉強目的の記事です)
(勉強目的の記事です)
K-meansは計算が早く便利だけど・・
K-means自体はシンプルで計算が早く、またその値を別のシンプルなモデルでstackingさせることで、最終的なモデルをシンプルなものにして、ある程度の精度を維持しつつAPIなんかでの遂次での処理に役立てたりもできます。
教師無しでも扱えるという点も、使いやすいモデルとしては魅力的な点です。
しかし一方で、最適なKの数を決めづらいという問題があります。
少なすぎても精度面で良くないですし、多すぎても困ってしまいます。
2次元や3次元であれば可視化して適切なKを選択できますが、さらに高次元になってくると難しくなってきます。
また、システムを組んで自動で回したりを検討する際にも、なるべくは人の手を介さずに自動で扱いたいものです。
様々なハイパーパラメーター調整用の手法を用いて適切なKを算出することもできますが、そこに至るまでの計算コストを考えると、K-meansの軽さの魅力が薄れてしまいます。
そこで、適切なKの数を高いパフォーマンスで決めてくれるX-meansというものがあるらしいので調べたりスクリプトを書いて試してみました。
X-meansの論文内容のメモ
- X-means: Extending K-means with Efficient Estimation of the Number of Clusters(論文PDFリンク)
- クラスター数を自動決定するk-meansアルゴリズムの拡張について(PDF論文リンク)
- 論文自体は約20年くらい前のもの。
- K-meansを何度も実行して最適化していくよりも大分早く対応ができる。
- 少ない数のクラスター分割からはじめて、それらをさらに分割してみて、分割が妥当であれば分割、そうでなければそこで止めてKの数が決定される。
- 判定時にはBIC(Bayesian Information Criterion: ベイズ情報量基準)という情報量基準が使われる。
- 後者の日本語の論文の方が少し後発で、前者の論文をさらに改善した内容になっている。
- K-means単体の計算コストの2倍強程の計算コストで、X-meansの計算が行える。
Pythonで動かしてみる
ネットで調べた感じ、自前で組んでいらっしゃる方と、ライブラリを使っている方がいらっしゃるようです。
まずは手っ取り早く試すために、ライブラリを使ってみましょう。
どうやらpyclusteringというライブラリで使えるそうで。
pipでインストールします。
$ pip install pyclustering
以下のような環境を今回使っています。
- Windows10
- Python3.7
- pyclustering==0.8.2
- numpy==1.15.4
- matplotlib==3.0.2
ダミーデータとして、4種類の分布のランダムな値を用意します。
まずは可視化しやすい2次元(x, y)で設定します。
import pyclustering
from pyclustering.cluster import xmeans
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
arr_1 = np.random.normal(scale=1.0, size=(1000, 2))
arr_2 = np.random.normal(scale=2.0, size=(3000, 2))
arr_3 = np.random.normal(scale=1.5, size=(2000, 2))
arr_4 = np.random.normal(scale=1.2, size=(500, 2))
arr_2[:, 0] += 10
arr_3[:, 0] += 4
arr_3[:, 1] += -7
arr_4[:, 0] += 11
arr_4[:, 1] += -9
X = np.concatenate([
arr_1,
arr_2,
arr_3,
arr_4,
])
X.shape
(6500, 2)
6500個の、ランダムなxとyの座標を持った行列です。
プロットすると以下のようになっています。
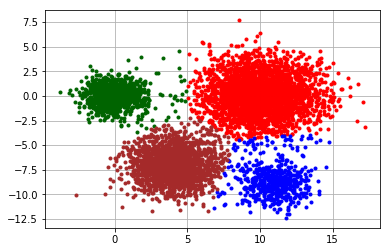
plt.scatter(x=X[:, 0], y=X[:, 1])
人が見れば4つのクラスターが必要そうだ、ということが分かります。
X-meansのモデルを組んでいきましょう。
initializer = xmeans.kmeans_plusplus_initializer(data=X, amount_centers=2)
初期化用のインスタンスを用意しました。
amount_centersの引数には、最初のクラスター数を設定します。
論文では普通に2で良さそうな記述があったので、特に理由がなければ2を設定します。
2から開始され、BICで妥当だと判定される限り分割されてクラスター数が増えていきます。
それらを使って処理します。
initial_centers = initializer.initialize()
xm = xmeans.xmeans(data=X, initial_centers=initial_centers)
xm.process()
xmeansの引数で、最大のKの制限や判定の閾値などを調整できるようです。今回はデフォルトのまま使います。
結果は、そのままライブラリでプロット用の機能が用意されているのでそちらを使います。
clusters = xm.get_clusters()
pyclustering.utils.draw_clusters(data=X, clusters=clusters)
Kを指定しなくても、よさげな感じにクラスを分けてくれました。
おまけで、3次元で試してみる
3次元まではそのままライブラリで同じような感じでプロットできるようなので試してみます。
arr_1 = np.random.normal(scale=1.0, size=(1000, 3))
arr_2 = np.random.normal(scale=2.0, size=(3000, 3))
arr_3 = np.random.normal(scale=1.5, size=(2000, 3))
arr_4 = np.random.normal(scale=1.2, size=(500, 3))
arr_1[:, 2] += 13
arr_2[:, 0] += 10
arr_2[:, 1] += 3
arr_2[:, 2] += -15
arr_3[:, 0] += 4
arr_3[:, 1] += -7
arr_3[:, 2] += 5
arr_4[:, 0] += 11
arr_4[:, 1] += -9
arr_4[:, 2] += 10
X = np.concatenate([
arr_1,
arr_2,
arr_3,
arr_4,
])
initializer = xmeans.kmeans_plusplus_initializer(data=X, amount_centers=2)
initial_centers = initializer.initialize()
xm = xmeans.xmeans(data=X, initial_centers=initial_centers)
xm.process()
clusters = xm.get_clusters()
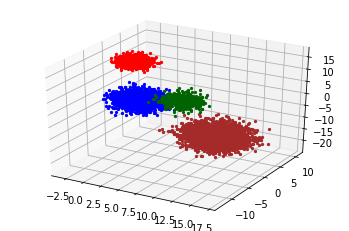
ax = pyclustering.utils.draw_clusters(data=X, clusters=clusters)
それっぽい感じに分けられました。
現実問題だと、特徴量を大分多く扱う必要があったりして、PCAなんかを使わないとうまいことK-meansやX-meansなどが動作してくれない気配もしていますが、そのあたりはちょっと今良さそうなデータセットがさくっと見つからなかったので今回は見送ります。仕事でも少し試しているので、もし有益そうなら後日記事にします。
いままで知らなかったのだが、常套手段らしい。
...
どう解決するか?
あらかじめ、別の空間に射影しておき、その空間でクラスターに分離してしまえばよい。
つまり、PCAで新しい軸ではられる空間に射影しておき、その空間上でkmeansクラスタリングを行うのだ。
PCAとkmeansを組み合わせた分析
ボロノイ図
こちらもおまけ気味ですが、少しボロノイ図について調べたり動かしてみたりしていたのでメモとして記載しておきます。
ボロノイ図ってなんだ
平面においては、複数個の点に対して、それ以外の他の点がどの点に近いかによって領域分けされた図がボロノイ図。領域の境界線は各々の点の二等分線の一部となる。
Python, SciPy, Matplotlibでドロネー図・ボロノイ図をプロット
ボロノイ分割はK-meansなんかのアルゴリズムで使われ、それぞれのクラスターの中心点同士の境界線を表したのがボロノイ図となります。
Pythonで描いてみる
SciPyを使うと簡単に描写できるようです。
使う環境(都合により先ほどとは別の環境で試しています) :
- Ubuntu環境
- Python 3.6.1 :: Anaconda 4.4.0 (64-bit)
- numpy==1.16.2
- scipy==1.2.1
- matplotlib==2.0.2
適当な6個のxとyの座標を格納した行列を用意します。
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import scipy
from scipy.spatial import voronoi_plot_2d, Voronoi
%matplotlib inline
plt.style.use('ggplot')
point_arr = np.array([
[10, 10],
[50, 30],
[60, 40],
[30, 80],
[20, 40],
[80, 40],
])
point_arr.shape
(6, 2)
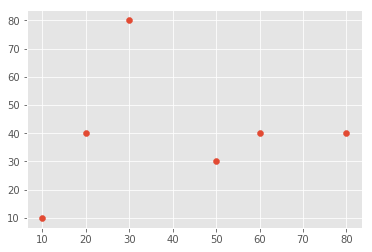
散布図でプロットすると以下のようになっています。
_ = plt.scatter(x=point_arr[:, 0], y=point_arr[:, 1])
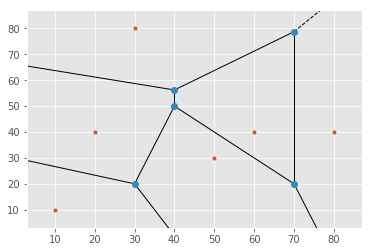
ボロノイ図を描写します。
といっても、座標の行列をSciPyのVornoiクラスに放り込んで、vornoi_plot_2d関数に入れるだけでプロットは終わりです。
vor = Voronoi(points=point_arr)
_ = voronoi_plot_2d(vor=vor)
図の青い点の座標は、vertices属性に行列で格納されています。
vor.vertices
array([[ 150. , -220. ],
[-435. , 175. ],
[ 30. , 20. ],
[ 70. , 78.75],
[ 70. , 20. ],
[ 40. , 56.25],
[ 40. , 50. ]])
※最初の2行の座標は、プロット外の見えないところにあります。
特に悩むこともなく、シンプルでいいですね。
参考
- 機械学習のための特徴量エンジニアリング ―その原理とPythonによる実践の本を参考にさせていただきました。別のドメインからやってきた人間なので、知らない古典的な手法など、いろいろ知ることができました。
- X-means: Extending K-means with Efficient Estimation of the Number of Clusters(論文PDFリンク)
- クラスタ数を自動推定するX-means法を調べてみた
- クラスター数を自動決定するk-meansアルゴリズムの拡張について(PDF論文リンク)
- x-meansでクラスタリング【python】
- PCAとkmeansを組み合わせた分析
- Python, SciPy, Matplotlibでドロネー図・ボロノイ図をプロット