背景
前回、k-meansの最適なk数ってどうやって探すの?って記事を書きました
↓
コメント欄

というわけで、『X-means』を調べました
クラスタ数を自動推定するX-means法について
- Pelleg and Moore (2000)が提案したK-meansの拡張アルゴリズム。
- クラスター数Kを自動決定する
- k-meansをデータ数が多くても高速に動くようなアルゴリズムに工夫する
という点が、従来のk-meansとの差分。
"x-means"でググると最初に出てくる2本のpopularっぽい論文
-
- x-meansの提案論文
-
クラスター数を自動決定するk-meansアルゴリズムの拡張について | 大学入試センター 研究開発部 (2000)
- 日本人作
- 上記の元祖論文と同年に出された x-meansの改良版についての論文
- こちらは著者によるRでの実装コードが公開されている
x-means概要
-
k-meansの逐次繰り返しとBICによる分割停止基準を用いて最適なクラスター数を決定する
-
BICの計算方法にバリエーションがある
- 基本的なアイデアは「データは、重心の近くにガウス分布している」ということを仮定して、
- 確率分布の概念を導入し、そこから尤度という概念が生まれるので、
- BICが計算できるという流れ
-
x-meansではk-meansを再帰的に呼び出し利用をしている
- k-meansの欠点(初期値依存性)をひきづっている
- クラスターは計算毎に少しづつ変わる
- しかし、クラスターサイズは安定してので最適なクラスター数の目安にはなる
- k-meansの欠点(初期値依存性)をひきづっている
-
先験情報が全く無い時に、発見的な方法に拠らずk-meansのおおよそ2倍強の計算量で最適なクラスター数を求めることができる
計算の流れ
大雑把な流れは、
- 少ないクラスター数でk-meansして、
- 出来たクラスターを2-meansして、クラスターを分割し、
- もしBICが大きくなったら、採用
- 2に戻る
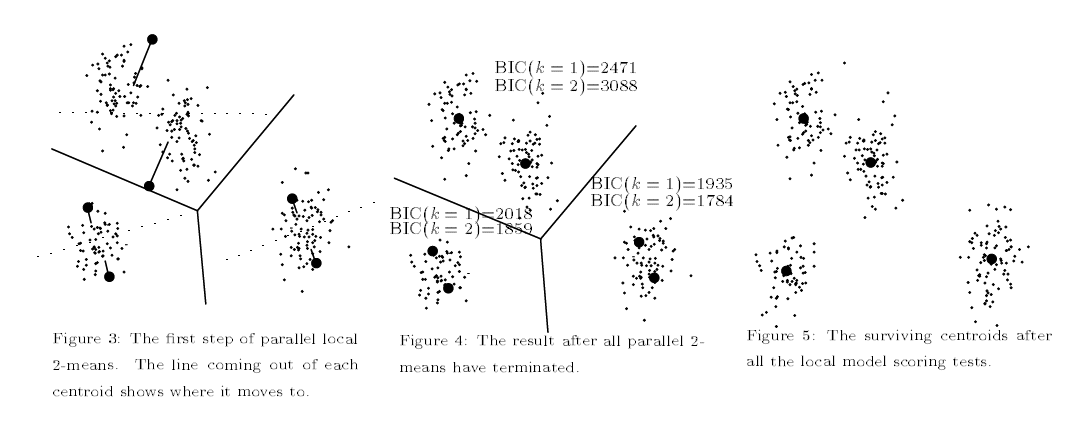
1の論文からFig引用
- (論文から引用)正解のクラスター数が5個の時の精度比較
- AICよりもBICで評価させた時のほうが正解クラスター数を多く出す
- AICでは比較的大きめのクラスター数を出す傾向がある
- 発見的方法(k-meansで手動でk数を指定していく方法)の結果がBICの結果と近い(手動で出した結果と同じならそれを自動で行うx-meanの方が優秀!)
2つの論文のロジックの違い
1 の元祖論文の概要
- 全てのクラスターで同じ分散でデータが散らばっていることを暗黙のうちに仮定している
2 の改良ロジック論文の概要
- クラスターの大きさによって重心が違うはずなので、そこも推定するようにロジックを作っている
その他、x-meansに関するブログ記事:
- Pythonでx-means法を実装した
- x-means (OpenCVのサンプルにおいて、k-meansを使った減色/画像分割処理をx-meansで置き換えた記事)
- x-means法
- Rでk-means法とその拡張2 x-means編 | サボタージュ禁止のおさぼり日記
PythonでのX-meansスクリプト
Pythonでx-means法を実装した [Gistコード] をコピペ
# -*- coding: utf-8 -*-
import numpy as np
from scipy import stats
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from IPython.display import display, HTML # Jupyter notebook用
%matplotlib inline
class XMeans:
"""
x-means法を行うクラス
"""
def __init__(self, k_init = 2, **k_means_args):
"""
k_init : The initial number of clusters applied to KMeans()
"""
self.k_init = k_init
self.k_means_args = k_means_args
def fit(self, X):
"""
x-means法を使ってデータXをクラスタリングする
X : array-like or sparse matrix, shape=(n_samples, n_features)
"""
self.__clusters = []
clusters = self.Cluster.build(X, KMeans(self.k_init, **self.k_means_args).fit(X))
self.__recursively_split(clusters)
self.labels_ = np.empty(X.shape[0], dtype = np.intp)
for i, c in enumerate(self.__clusters):
self.labels_[c.index] = i
self.cluster_centers_ = np.array([c.center for c in self.__clusters])
self.cluster_log_likelihoods_ = np.array([c.log_likelihood() for c in self.__clusters])
self.cluster_sizes_ = np.array([c.size for c in self.__clusters])
return self
def __recursively_split(self, clusters):
"""
引数のclustersを再帰的に分割する
clusters : list-like object, which contains instances of 'XMeans.Cluster'
'XMeans.Cluster'のインスタンスを含むリスト型オブジェクト
"""
for cluster in clusters:
if cluster.size <= 3:
self.__clusters.append(cluster)
continue
k_means = KMeans(2, **self.k_means_args).fit(cluster.data)
c1, c2 = self.Cluster.build(cluster.data, k_means, cluster.index)
beta = np.linalg.norm(c1.center - c2.center) / np.sqrt(np.linalg.det(c1.cov) + np.linalg.det(c2.cov))
alpha = 0.5 / stats.norm.cdf(beta)
bic = -2 * (cluster.size * np.log(alpha) + c1.log_likelihood() + c2.log_likelihood()) + 2 * cluster.df * np.log(cluster.size)
if bic < cluster.bic():
self.__recursively_split([c1, c2])
else:
self.__clusters.append(cluster)
class Cluster:
"""
k-means法によって生成されたクラスタに関する情報を持ち、尤度やBICの計算を行うクラス
"""
@classmethod
def build(cls, X, k_means, index = None):
if index == None:
index = np.array(range(0, X.shape[0]))
labels = range(0, k_means.get_params()["n_clusters"])
return tuple(cls(X, index, k_means, label) for label in labels)
# index: Xの各行におけるサンプルが元データの何行目のものかを示すベクトル
def __init__(self, X, index, k_means, label):
self.data = X[k_means.labels_ == label]
self.index = index[k_means.labels_ == label]
self.size = self.data.shape[0]
self.df = self.data.shape[1] * (self.data.shape[1] + 3) / 2
self.center = k_means.cluster_centers_[label]
self.cov = np.cov(self.data.T)
def log_likelihood(self):
return sum(stats.multivariate_normal.logpdf(x, self.center, self.cov) for x in self.data)
def bic(self):
return -2 * self.log_likelihood() + self.df * np.log(self.size)
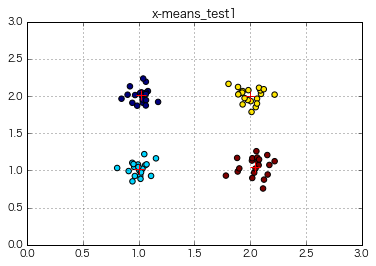
if __name__ == "__main__":
import matplotlib.pyplot as plt
# データの準備
x = np.array([np.random.normal(loc, 0.1, 20) for loc in np.repeat([1,2], 2)]).flatten() #ランダムな80個の数を生成
y = np.array([np.random.normal(loc, 0.1, 20) for loc in np.tile([1,2], 2)]).flatten() #ランダムな80個の数を生成
# クラスタリングの実行
x_means = XMeans(random_state = 1).fit(np.c_[x,y])
print(x_means.labels_)
print(x_means.cluster_centers_)
print(x_means.cluster_log_likelihoods_)
print(x_means.cluster_sizes_)
# 結果をプロット
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "+", s = 100)
plt.xlim(0, 3)
plt.ylim(0, 3)
plt.title("x-means_test1")
plt.legend()
plt.grid()
plt.show()
# plt.savefig("clustering.png", dpi = 200)
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2]
[[ 1.01854145 2.00982242]
[ 1.00199794 1.02110352]
[ 2.00022392 2.00435037]
[ 2.04408807 1.0518478 ]]
[ 42.91288569 44.48049658 37.32131967 29.6422041 ]
[20 20 20 20]
⇒ 4クラスターのデータに対してx-meansを行い、明示的なk数を指定しなくても確かに4クラスターに分けた!
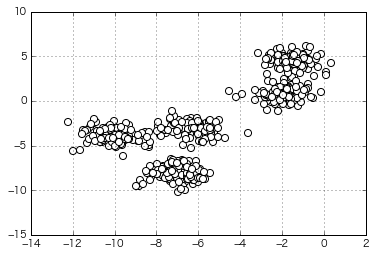
もう少しそれっぽいデータをクラスタリングさせてみる
(生成時のクラスター指定数は一応5)
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=5,
cluster_std=0.8,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
x =X[:,0]
y =X[:,1]
X=np.c_[x,y]
plt.scatter(x,y,c='white',marker='o',s=50)
plt.grid()
plt.show()
if __name__ == "__main__":
import matplotlib.pyplot as plt
# クラスタリングの実行
x_means = XMeans(random_state = 1).fit(np.c_[X])
# 結果をプロット
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
plt.title("x-means_test2")
plt.grid()
plt.show()
⇒ これもちゃんと分けた!
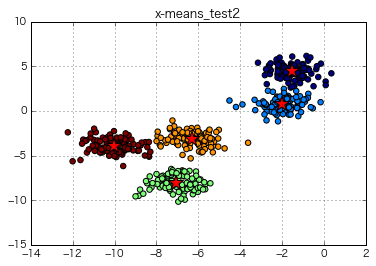
さらにモヤッとしたデータをクラスタリングさせてみる
(生成時のクラスター指定数は一応8)
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=8,
cluster_std=1.5,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
x =X[:,0]
y =X[:,1]
X=np.c_[x,y]
plt.scatter(X[:,0],X[:,1],c='white',marker='o',s=50)
plt.grid()
plt.show()
if __name__ == "__main__":
import matplotlib.pyplot as plt
# クラスタリングの実行
x_means = XMeans(random_state = 1).fit(np.c_[X])
# 結果をプロット
plt.rcParams["font.family"] = "Hiragino Kaku Gothic Pro"
plt.scatter(x, y, c = x_means.labels_, s = 30)
plt.scatter(x_means.cluster_centers_[:,0], x_means.cluster_centers_[:,1], c = "r", marker = "*", s = 250)
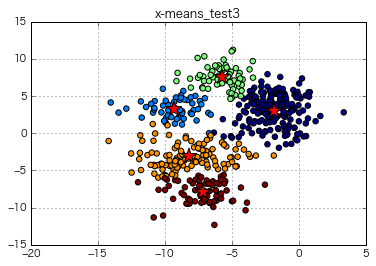
plt.title("x-means_test3")
plt.grid()
plt.show()
=> x-meansの自動クラスタリングでは、最適なクラスタ数を"5"として計算。それっぽく分けている感。
性懲りもなくまたエルボー図書いてみる
エルボー図の見方については前回の記事を参照
(クラスター1~10までのクラスター内誤差平方和をまとめて出力)
distortions = []
for i in range(1,11): # 1~10クラスタまで一気に計算
km = KMeans(n_clusters=i, # クラスターの個数
init='k-means++', # k-means++法によりクラスタ中心を選択
n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数 default: '10' 実行したうちもっとSSE値が小さいモデルを最終モデルとして選択
max_iter=300, # k-meansアルゴリズムの内部の最大イテレーション回数 default: '300'
random_state=0) # セントロイドの初期化に用いる乱数発生器の状態
km.fit(X) # クラスタリングの計算を実行
distortions.append(km.inertia_) # km.fitするとkm.inertia_が求まる
y_km = km.fit_predict(X)
plt.plot(range(1,11),distortions,marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
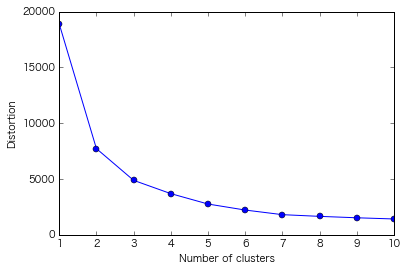
plt.show()
=> この図から最適なクラスタ数を"5"と判断するのはやはり難しい
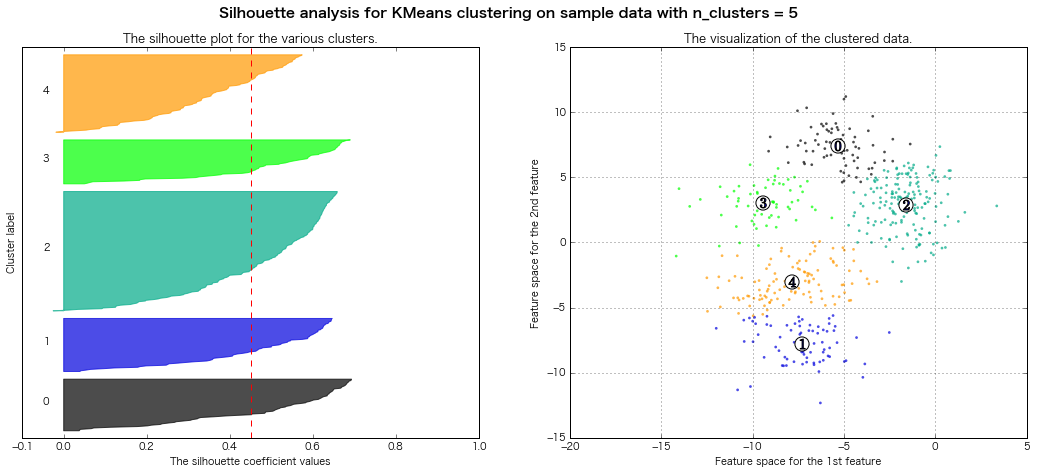
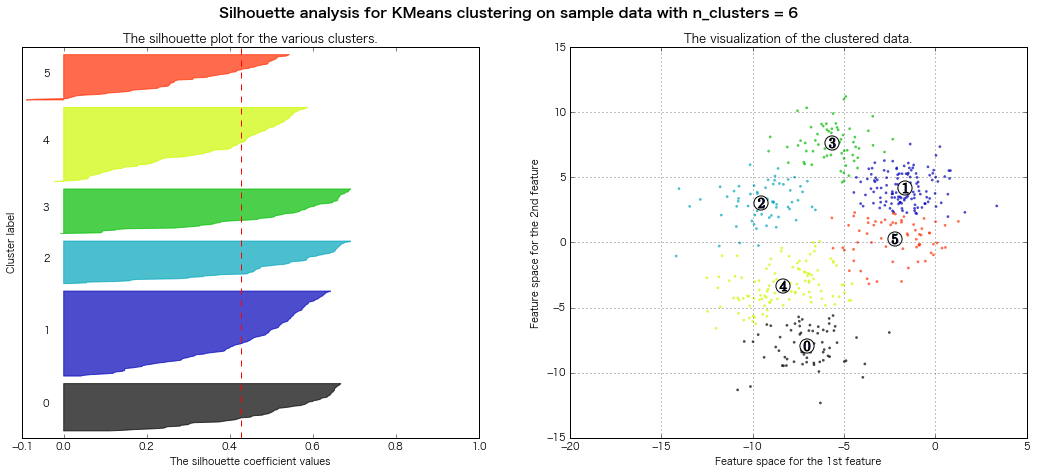
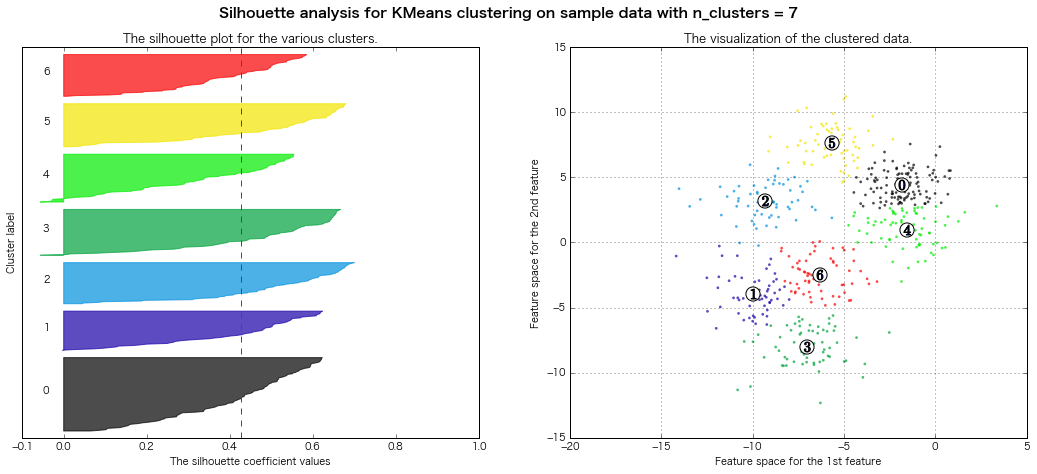
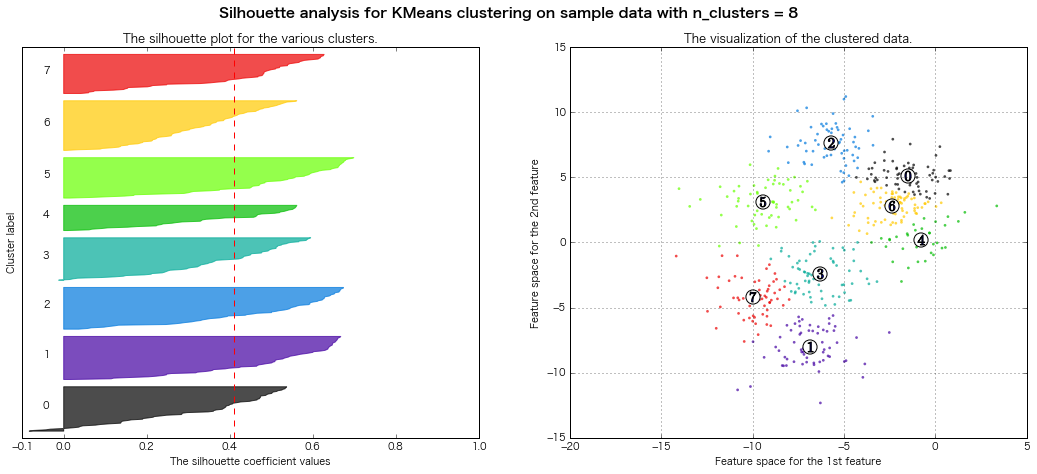
性懲りもなくまたシルエット図書いてみる
シルエット図の見方については前回の記事を参照
(クラスター3~8までのシルエット図をまとめて出力)
scikit-learn公式のページのコードを拝借(一部書き換え)
km = KMeans(n_clusters=5, # クラスターの個数
init='k-means++', # k-means++法によりクラスタ中心を選択
n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数 default: '10' 実行したうちもっとSSE値が小さいモデルを最終モデルとして選択
max_iter=300, # k-meansアルゴリズムの内部の最大イテレーション回数 default: '300'
random_state=0) # セントロイドの初期化に用いる乱数発生器の状態
y_km = km.fit_predict(X)
from __future__ import print_function
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
print(__doc__)
# Generating the sample data from make_blobs
X, y = make_blobs(n_samples=500,
n_features=2,
centers=8,
cluster_std=1.5,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
range_n_clusters = [3, 4, 5, 6, 7, 8]
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=1)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels,metric='euclidean')
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhoutte score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors)
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1],
marker='o', c="white", alpha=1, s=200)
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1, s=100)
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.grid()
plt.show()
Automatically created module for IPython interactive environment
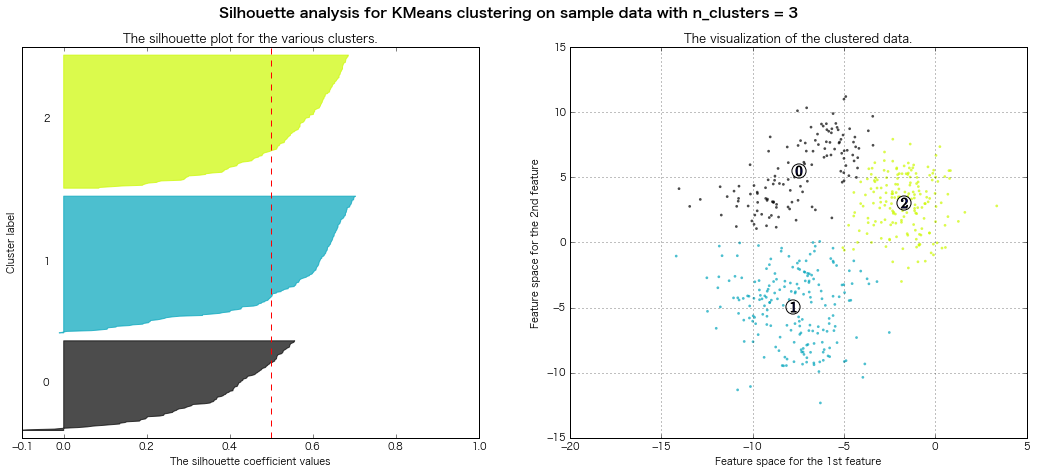
For n_clusters = 3 The average silhouette_score is : 0.500273979793
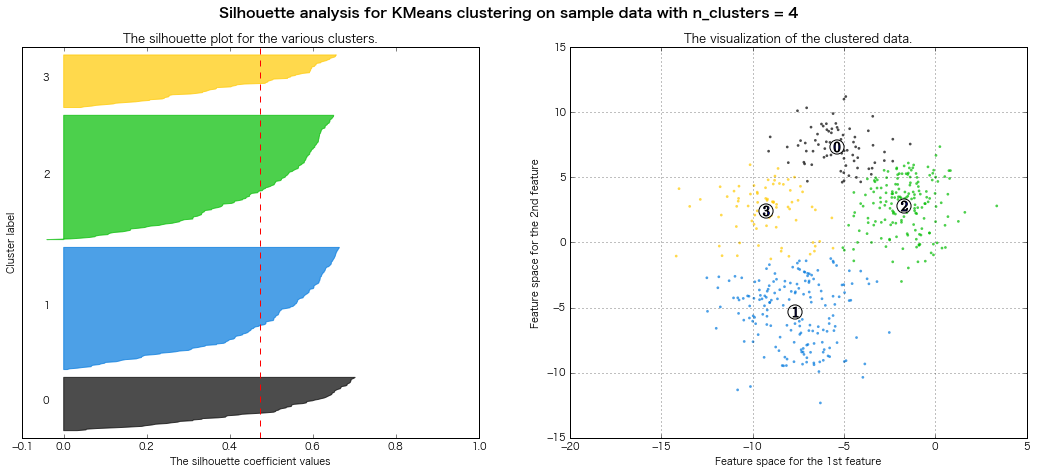
For n_clusters = 4 The average silhouette_score is : 0.473805434223
For n_clusters = 5 The average silhouette_score is : 0.451524016461
For n_clusters = 6 The average silhouette_score is : 0.428239776719
For n_clusters = 7 The average silhouette_score is : 0.427688325647
For n_clusters = 8 The average silhouette_score is : 0.409792863353
=> シルエット図の評価法的には、クラスター数7とか8とかが良さそうな感じがする
結論
- x-meansは確かに良い感じにクラスタリングしてくれそう
- ただし、そのクラスター数を"答え合わせ"する方法も無いし、やはり「最適なクラスター数の"目安"を得る」ために利用するという感じか?
- エルボー図から最適なクラスター数の目安を得るのはやはり難しい...?
- シルエット法も同じく...
⇒ 結局、クラスタリングの目的に沿って、解釈しやすい結果を得たクラスターをある程度恣意的に選択する感じになるのか?
Appendix(内容理解のためにいろいろ調べたこと)
x-means法のロジックを調べよう!→ベイジアン情報量基準(BIC)がわからん→そもそもAICもきちんとはわからん→尤度 is 結局何?→尤度を求めるには最尤推定以外にもベイズ推定というものがあってじゃな...
そこから延々と続くyak shaving
"Acutally, my whole life is just one big yak shaving exercise." - Joi Ito
赤池情報量規準:AIC(Akaike's Information Criterion)
最適なパラメータ数を持つモデルを選択するための指標
- あるデータに対して作成されたモデルはパラメータを増やすほど既存のデータとの適合度を高めることができるが、過学習に陥る
- 過学習に陥らないためにはモデル化のパラメータ数を抑える必要があるが、実際にどの数に抑えるかは難しい問題である
- モデルでAICを計算し、最小の値を示せば多くの場合良いモデル選択ができる
- AICはモデルの対数尤度とパラメータの数で構成されているので、精度と複雑さのトレードオフがいい感じに記述できている
$$AIC = -2\ln{}L+2k$$ $$L \cdots あるモデルにおける尤度関数の最大値$$ $$k \cdots モデルのパラメータの数$$
- 式の第1項がモデルへの当てはまりの良さを、第2項がモデルの複雑さに対するペナルティを表す
- 第2項は、パラメーター数が少ない方がOverfitting問題を避けることができるので、パラメーター数を押さえたモデルに優位に働く
- あてはまりが良くても滅茶苦茶複雑なモデルは好ましくないということで、当てはまりが良く、なおかつシンプルなモデルが志向される指標
- 対象となる全てのモデルでAICを計算して最小となるモデルを選択すると一般的には良いモデルが選択できるといえる
参考:
ベイジアン情報量基準:BIC(Bayesian Information Criterion)
- BICが最小の値を示せば多くの場合、良いモデル選択ができる
- AICと比べ、第2項のモデルの複雑さに対する罰則項にサンプルサイズサイズも考慮した指標
- AICとは異なり、この基準による選択は一致性(標本数が多くなると真の次数をもたらすこと)を持つ
$$BIC = -2\ln{}L+k\cdot\ln{(n)}$$ $$L \cdots あるモデルにおける尤度関数の最大値$$ $$k \cdots モデルのパラメータの個数$$ $$n \cdots 標本の大きさあるいは観測の数$$
参考:
Bayesian Information Criterion | wikipedia
AICとBICの違い
-
目的の違い
- 予測精度を上げるためにモデル選択をするのであればAICを用いる
- データが生成されている構造を知ろうとするのであればBICを用いる
-
数式的な違い
- 第2項の罰則項
- AICでは、罰則項がサンプルサイズによらずサンプルサイズが大きいときに第1項の比重が大きくなり複雑なモデルが選ばれがち
- BICでは、罰則項でサンプルサイズが考慮されるのでAICよりもシンプルなモデルが選ばれがち
- 第2項の罰則項
-
モデルパラメータの推測ストラテジの違い
-
AICは最尤推定によって尤度関数の最大値を決定
-
BICはベイズ推定によって尤度関数の最大値を決定
-
ただし、必ずしもこのように用いなければならないというコンセンサスはない
-
参考:
尤度の復習
「そもそも尤度ってなんだったっけ?」の復習
得られたデータから考えたときのモデルの尤もらしさを尤度という。
引用元
尤度関数の基本概念は、**「サンプリングしてデータが観測された後、そのデータは元々どういうパラメーターを持つ確率分布から生まれたものだったか?」**と言う問いに答えるためのものです。
引用元
尤度とは,確率とそっくりです。しかし,考え方が違います。
確率はパラメータを固定してデータが変化しますが,尤度はデータを固定してパラメータが変化するのです。
引用元
参考:
#### 最尤推定とは 尤度が最大となるとき = 推定したいモデル(確率分布:基本はガウス分布)のパラメータ(ガウス分布の場合は平均と分散)がわかる
### 最尤推定とベイズ推定の違い
| is何? | 方法 | つまり | |
|---|---|---|---|
| 最尤推定 | 尤度を最大化するパラメータを計算する方法 | 尤度のみでパラメータを推定(事前確率とか考えない) | 今取得したデータの確率のみ使用してパラメータを推定 |
| ベイズ推定 | 事後確率を最大化するパラメータを計算する方法 | 事前確率と尤度の両方を使用してパラメータを推定 | 今取得したデータだけでなく、事前確率・事後確率も使用してパラメータを推定 |
参考:
#### 最尤推定とベイズ推定、どっちを使えば良いの?
- (大雑把に言えば)基本的にはどちらも同じ
- 最大の違いは**「事前確率」を考えるかどうか**
- 最尤推定は事前確率を考えない(=一様分布を仮定している、とも言える)。つまり何にも情報がない状態をスタートとしている
- 事前確率が一様でない場合は、最尤推定とベイズ推定の結果は異なる
- ベイズ推定では、最適な事前確率を設定できると、より精度の高い推定を行うことができる
- ベイズ推定の方がより多くの情報を活かした推定となっている
- 事前確率の設定は主観的なものになりがち。このことが最尤派とベイズ派の論争の中心となってるらしい
- 特に事前に何の予測もないor最適な事前分布がわからなければ「無情報分布」という事前分布を利用する(多くのプログラムはデフォルトが無情報分布になっている)
参考: 従来の推定法とベイズ推定法の違い | Sunny side up!
ベイズ推定について
ベイズ推定の適合度で代表的な指標はベイズファクター(BF)
- BFは2つのモデルの尤度の比を表す
- BFはBIC(ベイズ情報量基準)に近似可能
- 2つのモデルのBICの差 ≒ BFの対数の2倍 (※近似しているだけで別物であることに注意)
$$ 仮説H_0をもつモデルM_0と仮説H_1を持つモデルM_1が存在する時、$$
$$\frac{P(H_1|D)}{P(H_0|D)}=\frac{P(D|H_1)P(H_1)}{P(D|H_0)P(H_0)} \cdots ①$$
$$\frac{P(D|H_1)P(H_1)}{P(D|H_0)P(H_0)}=\frac{P(D|H_1)}{P(D|H_0)}×\frac{P(H_1)}{P(H_0)} \cdots ②$$
$$ ①、②より $$
$$\frac{P(D|H_1)}{P(D|H_0)} = \frac{P(H_1|D)}{P(H_0|D)} × \frac{P(H_0)}{P(H_1)}$$
$$つまり$$
$$尤度の比(ベイズファクター) = 事後確率の比 × 事前確率の比 $$
参考:ベイズファクターとモデル選択 | SlideShare
ベイズファクターの基準
| BF | 2logBF (≒BIC)| M0と比べたM1に対する判断 |
|:-----------|:------------|:------------|:------------|
| BF<1| 2logBF<0 | M0のほうが良い |
| 1<BF<3| 0<2logBF<2 | M1のほうがかろうじて優れている |
| 3<BF<12| 2<2logBF<5 |M1のほうが優れている(Positive)|
| 12<BF<150| 5<2logBF<10 | M1のほうがかなり優れている(Strong)|
| 150<BF| 10<2logBF | M1のほうが非常に優れている(Very Strong)|
モデル評価にベイズファクターを用いることのメリット・問題点
■メリット
-
帰無仮説の呪縛からの開放
- 伝統的な検定は「帰無仮説」と「対立仮説」という構図
- しかしベイズファクターなら「独立する2つのモデル(仮説)」を比較するだけ
- 別に「帰無仮説」なんてなくていい
- しかしベイズファクターなら「独立する2つのモデル(仮説)」を比較するだけ
- 伝統的な検定は「帰無仮説」と「対立仮説」という構図
-
正規分布の呪縛からの開放
- ベイズの式には、事前分布を組み込んでいる
- 「事前分布は正規分布でなくていい」 → より柔軟な統計モデルをあてはめて検討可能 ・・・ベイズ推定が利用される
- ベイズの式には、事前分布を組み込んでいる
■問題点
- ベイズファクターは2つのモデルの「尤度の比」
- 数値の大小は、「2つを比較してどっちがいいか」にしかならない
- 複数の指標を算出して、トータルで考えていくのが良い
- 数値の大小は、「2つを比較してどっちがいいか」にしかならない
- 計算が大変
- パラメータが増えたり事前分布などによって大変になる
その他、ベイズ推定の利点と欠点についてはこちらが詳しい
その他 最適なモデルを選ぶための指標(目安)となるもの
-
偏差情報量基準: DIC(Deviance Information Criterion)
-
事後予測P値
-
AICやBICなどの指標の問題点として、潜在変数などが入った特異モデルには適用できない点が挙げられる
- これらに対応するために、FIC(Factorized Information Criterion)やFAB(Factorized Asymptotic Bayesian inference)という情報量もあるらしい