day1
Section1-入力層-中間層
Section2-活性化関数
Section3-出力層
Section4-勾配降下法
Section5-誤差逆伝播法
day2
Section1-勾配消失問題
Section2-学習率最適化手法
Section3-過学習
Section4-畳み込みNNの概念
Section5-最新のCNN
day1
そもそもDeep Learningは何をしたいのか。
→ 明示的なプログラムの代わりに、中間層のパラメータにより入力から出力に変換するモデルを構築すること。
学習によってパラメータ(バイアスと重み)を調整する。
1 Section1-入力層-中間層
特徴量(入力値)の線形写像
(中間層のノードがひとつの例)

ノードを複数にする場合はそれに応じてパラメータも増えていく。
中間層を増やしていく場合もパラメータが増えていく。
ノードや中間層が多いほど関数による複雑な表現が可能になる。
2 Section2-活性化関数
前Sectionの画像の、u を z に変換するところ
ここで非線形に変換するのがポイント
(これが線形変換だと分けている意味が無くなってしまう。Section1の線形写像が線形なので、線形→線形を式変形するとひとつの式にまとめることができてしまうため。)
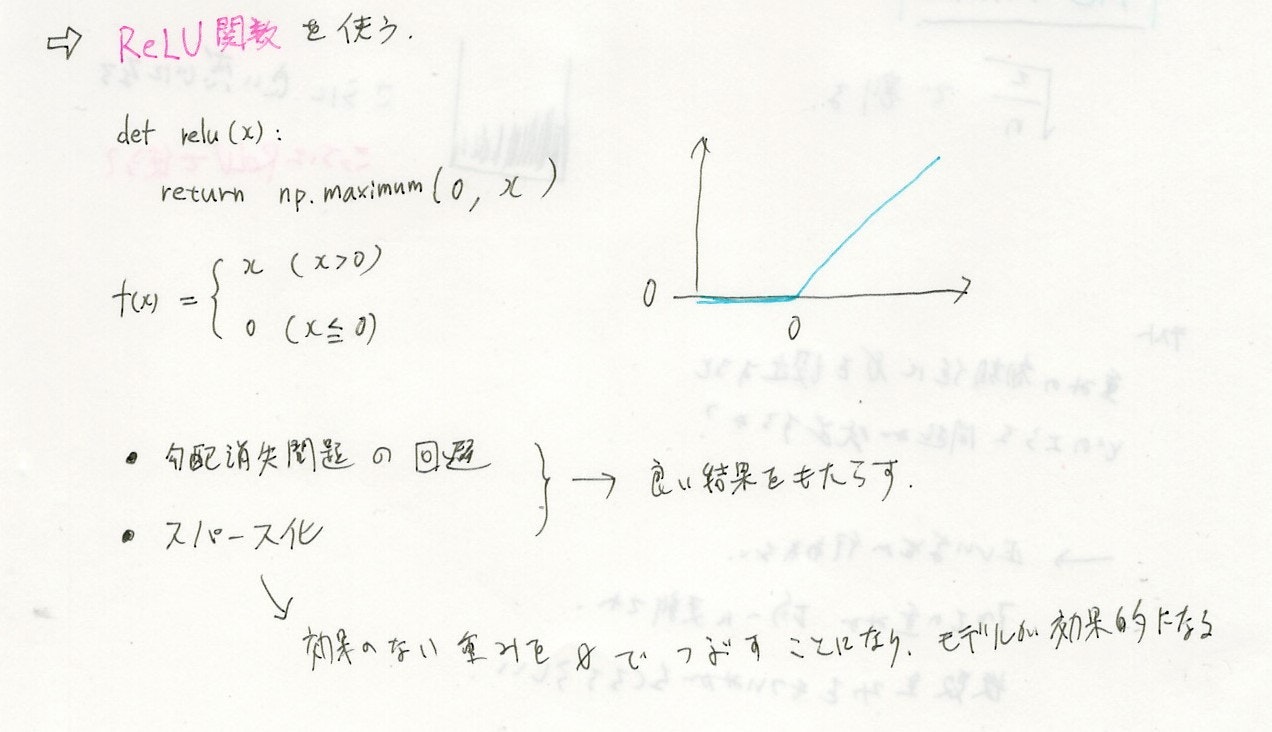
ReLU関数を使う。
(Rectified Liner Unit) 名前はリニアがついているけど途中で折れ曲がっているので線形ではない。
中間層の活性化関数、出力層の活性化関数は、意味が異なる。
中間層は強弱の変化
出力層は確率への変換
3 Section3-出力層
出力層の活性化関数
| 回帰 | 二値分類 | 多クラス分類 | |
|---|---|---|---|
| 活性化関数 | 恒等写像 (何もしない) |
シグモイド | ソフトマックス |
| 誤差関数 | 二乗誤差 平均二乗誤差 |
交差エントロピー | 交差エントロピー |
タスクの種類によって、使用する関数は異なる。
4 Section4-勾配降下法
勾配降下法
確率的勾配降下法
ランダムに抽出して勾配降下法を実施する。
ミニバッチ勾配降下法
バッチ学習とオンライン学習の中間にあるものがミニバッチ学習
バッチ学習は、
全てをメモリに読み込んで全データから得られた誤差で、1回更新する。
1エポックに1回更新する
これはバッチサイズ=全サンプル数を意味する。
オンライン学習は、
1個のデータにつき
1回パラメータを更新
これはバッチサイズ=1を意味する。
ミニバッチ学習はこれらの中間
(というか通常DLをするときは大抵はミニバッチ学習を使う)
バッチごとに小分けにして、バッチごとにパラメータ更新する。
全サンプル数が1000件の場合にバッチサイズ250とすると、4つのグループに分かれる。
(イテレートを4回実施することになる)
5 Section5-誤差逆伝播法
数値微分は計算量が多くなってしまうので使えない。
→ 誤差逆伝播(ごさぎゃくでんぱ)法を使う。

day2
6 Section1-勾配消失問題
勾配消失問題への対処
- 活性化関数の選択
- 重みの初期化
- バッチ正規化
中間層が増えるにつれて、下位層のパラメータが変化せず、学習が進まなくなる。
原因:1より小さい値を繰り返し掛け算するため。
※ シグモイドはその代表的な原因とされる。(微分すると最大でも0.25なので)
解決策
活性化関数の選択
 ##### 重みの初期化
##### 重みの初期化
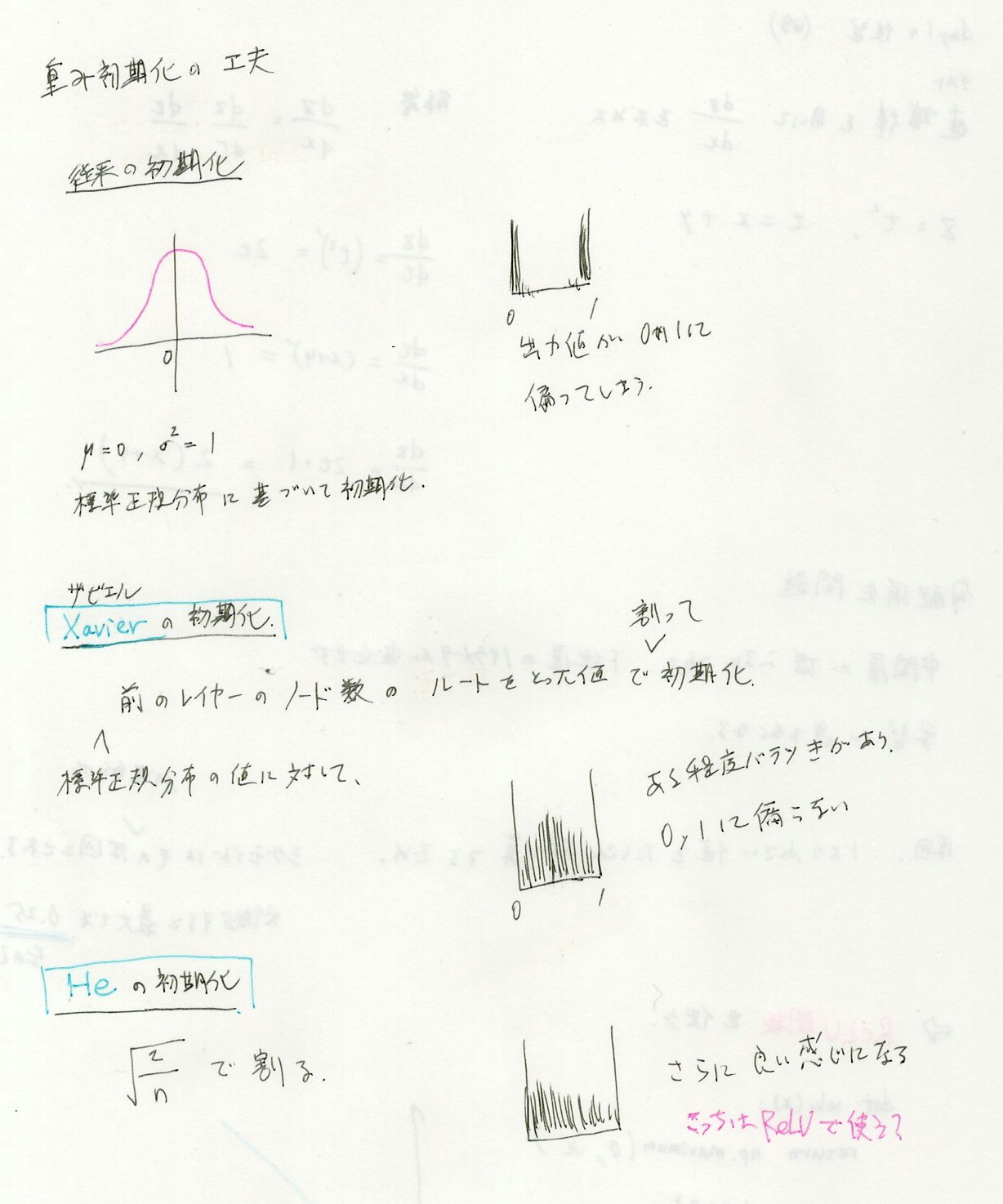
重みの初期化に0を設定すると、どのような問題が発生するか?
→ 正しい学習が行われない。すべての重みが均一に苦心され、複数の重みを持っている意味がなくなる。
バッチ正規化

バッチ正規化のメリット
- 学習の安定化、速度向上。
- 過学習が発生しづらくなる。学習データの極端なばらつきが無くなる。
- 大きな学習係数が使えるようになる。
- 伝播中にパラメータがスケールの影響を受けにくくなる
- 係数を大きくしても勾配消失や勾配爆発が起きにくくなる
- その結果速度が向上する
- 正規化の効果がある
- 論文に、L2正則化やDropoutの必要性が下がると書かれている
- これらを使わないことによってもその分速度が向上する
- 重みの初期値への依存性が少なくなる。
7 Section2-学習率最適化手法
最適化=Optimize
パラメータの更新を行うときにうまい具合に調整する手法
SDG
w^{(t+1)} = w^t - \color{skyblue}{\eta} \nabla E \\
この \color{skyblue}{\eta}(学習率) をうまい具合に調整する。
これは単純なSDGの式。
勾配の分だけパラメータを減らせばlossが減るので(一定の割合を掛けて)引き算する、という考え方。
self.param[key] -= self.lr * grad[key]
再急降下法もミニバッチSDGも更新の考え方は同じ。
違いはデータが複数あるときの扱い方で、
- 最急降下法 → 全部のデータを一気に使う
- 確率的勾配降下法 → ランダムにデータを一個ずつ選ぶ
- ミニバッチSGD → ランダムにデータをミニバッチに分けて、ミニバッチごとに処理
以下はSDGの考え方をもとに、改良したもの。
代表的な4つの手法
- モメンタム (ネステロフモメンタム)
- AdaGrad
- RMSProp
- Adam ※ 一番優秀
モメンタム
V_{t+1} = \color{crimson}{\alpha} V_t - \color{skyblue}{\eta} \nabla E \\
W^{(t+1)} = W^{(t)} + V_{t+1}
前回のVを覚えておいて使用する。
$ \color{skyblue}{\eta} $ は学習率
$ \color{crimson}{\alpha} $ は慣性(固定値) ← モメンタム係数
係数の移動平均のような動きをする。カクカクせずに滑らかな曲線状に動く。
移動平均を用いることで振動を抑制。
self.v[key] = self.momentum * self.v[key] - self.lr * grad[key]
param[key] += self.v[key]
ネステロフモメンタム
Nesterovの加速勾配法 (NAG) とも呼ぶ。
V_{t+1} = \color{crimson}{\alpha} V_t - \color{skyblue}{\eta} \frac{\partial L}{\partial(W_t + \color{crimson}{\alpha} V_t)} \\
W^{(t+1)} = W^{(t)} + V_{t+1}
他のアルゴリズムのように $ \nabla E $ でまとめずに、偏微分の式の中にハイパーパラメータを使用している。
この更新式はそのまま実装すると計算が大変になるため、実際は次のように式変形したものを実装する。
\Theta_t = W_t + \alpha V_t とおく。 \\
V_{t+1} = \alpha V_t - \eta \frac{\partial L}{\partial \Theta_t} \\
\Theta_{t+1} = \Theta_t + \alpha^2 V_t - (1 + \alpha) \eta \frac{\partial L }{\partial \Theta_t} \\
(E資格問題集より。この最後の変形がなぜこうなるか不明)
Wを更新する代わりに $ \Theta $ を更新していくことで、Wを更新していった場合と等価になるとのこと。
以下はparamsが $ \Theta $ を指している。
また、順番が上記の数式の2行目3行目が入れ替わったように書かれているが、
わざわざ正誤表で前半と後半を入れ替えているので、おそらくこのように先にparamを更新して、
加速のVは次に使うために後半で用意しておく、という流れになるのだと思う。
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
AdaGrad
h_0 = \theta \\
h_t = h_{t-1} + (\nabla E)^2 \\
W^{(t+1)} = W^{(t)} - \color{skyblue}{\eta} \frac{1}{\sqrt{h_t + \varepsilon }} \nabla E
誤差の2乗を蓄積してゆき、その逆数を誤差に乗じる。
だんだん学習率が小さくなっていく。
勾配のゆるやかな斜面に対して、ぶれないで最適化に近づけるが、
鞍点(あんてん)問題を引き起こすことがある。
self.h[key] = np.zeros_like(val) // 何らかの値で初期化
self.h[key] += grad[key] * grad[key]
params[key] -= self.lr * grad[key / (np.sqrt(self.h[key]) + le-7)
RMSProp
AdaGradのちょっと改良型
h_t = \color{crimson}{\alpha} h_{t-1} + (1-\color{crimson}{\alpha})(\nabla E)^2 \\
W^{(t+1)} = W^{(t)} - \color{skyblue}{\eta} \frac{1}{\sqrt{h_t} + \varepsilon } \nabla E
AdaGradでは $ \varepsilon $ が√に入っていてRMSPropには入っていないが本質的には大差ないらしい(論文に合わせているだけ)
メリット
局所解に陥りづらい。
ハイパラ調整がゆるくてもうまくいく場合が多い。
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grad[key] * grad[key]
params[key] -= self.lr * grad[key] / (np.sqrt(self.h[key]) + le-7)
Adam
最強オプティマイザー
これまでのいいところどりをしている。
以下の2つをミックスしている
- モメンタム系 いけるところに一気に行く。
- RMSProp系 過去の経験を活かす。
m_{t+1} = \color{crimson}{\rho_1} m_t + (1 - \color{crimson}{\rho_1}) \nabla E ... ① \\
\mu_{t+1} = \color{skyblue}{\rho_2} \mu_t + (1 - \color{skyblue}{\rho_2}) (\nabla E)^2 ... ② \\
\hat{m} = \frac{m_{t+1}}{1 - \color{crimson}{\rho_1}} ... ③ \\
\hat{\mu} = \frac{\mu_{t+1}}{1 - \color{skyblue}{\rho_2}} ... ④ \\
W_{t+1} = W_t - \eta \frac{1}{\sqrt{\hat{\mu}} + \varepsilon} \hat{m} ... ⑤
$ \eta $ :学習率
$ \rho_1 $ :減衰率1
$ \rho_2 $ :減衰率2
$ \varepsilon $ :微小な数値
初期値
$ m = 0、 \mu = 0 $
①でmがgの平均であることを期待していたのに、ずれてしまっているため補正を行っているのが③
(②、④も同様)
self.m[key] = self.rho1 * self.m[key] + (1 - self.rho1) * grads[key]
self.v[key] = self.rho2 * self.v[key] + (1 - self.rho2) * (grads[key] ** 2)
m = self.m[key] / (1 - self.rho1 ** self.iter)
v = self.v[key] / (1 - self.rho2 ** self.iter)
params[key] -= self.lr * m / (np.sqrt(v) + self.epsilon)
最適化アルゴリズム参考サイト
[AI入門] ディープラーニングの仕組み ~その4:最適化アルゴリズムを比較してみた~
【決定版】スーパーわかりやすい最適化アルゴリズム
勾配降下法の最適化アルゴリズム
最適化のテクニックを学ぼう!【作って理解するディープラーニング#7】
深層学習の最適化アルゴリズム
8 Section3-過学習
問題集は完ぺきに解けるけど、模試を受けるとあまり結果が良くないような状態
過学習=オーバーフィッティング=過剰適合
過学習の原因
- パラメータの数が多すぎる
- パラメータの値が適切でない
- ノードが多すぎる
ネットワークの自由度が高すぎる状態であるといえる。
→ シンプルな手法にするなどの対策が考えられる。次に説明する、正則化も有効。
また、
- 学習データ量の不足
- 学習データが偏っている
→ 学習データを増やす
正則化
→ ネットワークの自由度に制約をかける
→ 過学習を抑制できる
- L1正則化
- L2正則化
- Dropout
weight decay (荷重減衰)
過学習状態のときにNNの中で起きていること
重みが極端に大きくなっている箇所があり、
入力データのある部分だけを過大評価している。
⇒ 重みが極端に大きくならないように抑制
正則化項を加算。
L1正則化: P1ノルム
L2正則化: P2ノルム
損失関数に正則化項を加えると、正則化項がパラメータの大きさに対するペナルティとして働くことにより、極端なパラメータになるのを防ぐ。
正則化を用いて最適化を行う。
arg \ min \{ L(\boldsymbol{w}) + \lambda R(\boldsymbol{w}) \} \\
\boldsymbol{w}:パラメータ \\
L(\boldsymbol{w}):損失関数 Loss \ Function (\nabla E でもE(\boldsymbol{w})でも同じ) \\
R(\boldsymbol{w}):正則化項 Regularizer \\
\lambda :正則化パラメータ
Rの部分はL1またはL2で異なる。
L1 \ \ \ \ \lambda \sum_{i=0}^{n}|w_i| = ||x||_1 = \sum_{i}^n|x_1| \\
L2 \ \ \ \frac{\lambda}{2} \sum_{i=0}^{n}w_i^2 = ||x||_2 = \sqrt{\sum_{i}^n x_i^2}
Pノルムの一般化
||x||_p = \sqrt[p]{(|x_1|^p + |x_2|^p + \cdots + |x_n|^p )} \\
このように各々の項をp乗したものを全部足してp乗根をとる。
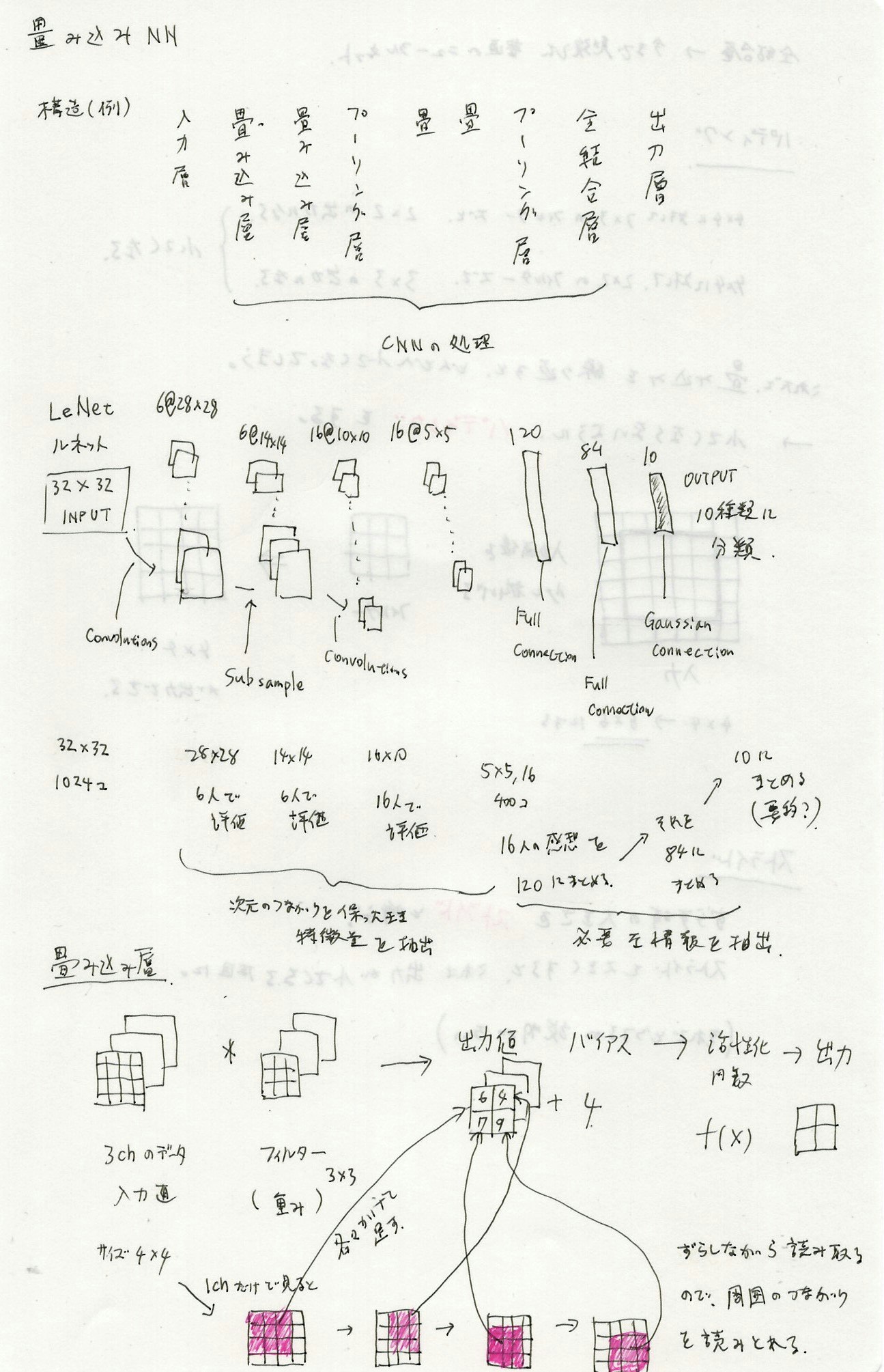
9 Section4-畳み込みNNの概念


そのほかにも、グローバルMaxPoolingやグローバルAveragePoolingなどがある。flattenよりもなぜかうまくいく。
グローバルがつくと、ひとつの面(チャネルごと)をまるごと平均化する。(例えば3チャネルの面があったらスカラー3つ(ベクトル)になる)
4096の全結合層にドロップアウトを適用することが多い。
10 Section5-最新のCNN
参考
(https://www.slideshare.net/ren4yu/ss-145689425)
(https://qiita.com/yu4u/items/7e93c454c9410c4b5427)
(https://deepsquare.jp/2020/04/resnet-densenet/)
cnnの歴史的な話
2012年 AlexNet
2013年 ZFNet
2014年 GoogleNet と VGGNet
2015年 ResNet ※ ここで人間超え
2016年 DenseNet
2017年 SENet
:
ResNetが1つの大きなブレークスルーであり,それ以降のモデルはほとんどがResNetの改良
AlexNet
2012年のILSVRCにおいて,従来の画像認識のデファクトスタンダードであった SIFT + Fisher Vector + SVM5 に大差をつけて優勝した。
ディープラーニングが注目されるきっかけになった。

ZFNet
2013年のILSVRC優勝モデル。
CNNの可視化を行い、AlexNetの問題点を発見したとある。
GoogleNet
2014年のILSVRC優勝モデル。
22層のネットワーク。
次のVGGは構造が単純だが、こちらは複雑。
Inceptionモジュールを使用する。
複数の畳み込み層やpooling層から構成される小さなモジュール(Inceptionモジュール)を通常の畳み込み層のように重ねていって1つの大きなCNNを作り上げている。
5×5 の畳み込みをするより、圧縮して5×5,3×3,1×1を行う方が次元が減るため、「スパースな畳み込み」とも呼ばれる
Global Average Pooling (GAP)、Auxiliary Lossも採用している。
VGG
2014年のILSVRC準優勝。
深いネットワーク構造が特徴、構造が単純。(といっても19層くらい?)
畳み込みサイズ3x3のみを使用して、CNNの深さが性能にどう影響するかを調査するような目的で作られたらしい。
ResNet
2015年のILSVRC優勝モデル。
152層ある。
CNNの代表格、代名詞的な存在
通常のネットワークのように単純にF(x)を次の層に渡していくのではなく、入力xもショートカットして一緒にわたす。
$$ H(x)=F(x)+x $$
このようなものをresidualモジュールと呼ぶ。
backpropagation時に勾配が直接下層に伝わるので深いネットワークでも効率的に学習できる。
Skip connectionを使用。
バッチ正規化(Batch Normalization)がこのresidualモジュールに組み込まれた。
ReLU + Heの初期化も使われている。
DenseNet
ResNetのように、もし前のレイヤーとスキップ接続で接続することによってパフォーマンスが向上するならば、その他のレイヤー全部に直接接続すればもっと精度がよくなるのでは?と考えた。
入力およびある層より前の層の出力がすべて入力となる。
層が密に結合しまくっている状態。(なのでDenseNetという)
メリット
- 勾配消失の削減
- 特徴伝達の強化
- 特徴の効率的な利用
- パラメータ数の削減
- 正則化効果の期待
SENet
Attentionが使われているとある。
その後の改良
Residualモジュールの改良
独自モジュールの利用
独自マクロアーキテクチャの利用
正則化
高速化を意識したアーキテクチャ
アーキテクチャの自動設計
さまざまな改良がされている。
最近のもの
物体検出
ディープラーニング以前は、HOGが有名。(2005年頃)(SVMを使っていた)
その後CNNを物体検出に応用するものとして以下のようなものが登場。
- R-CNN (CVPR 2014)
- Selective Search
- 色の似ている領域を取る
- Fast R-CNN (ICCV 2015)
- Selective Searchで取ってきた領域に対し、
分類と位置の調整を同時に行っている
- Selective Searchで取ってきた領域に対し、
- Faster R-CNN (NIPS 2015)
- Selective Searchを廃止
- それまでは物体候補の検出アルゴリズムは既存の手法だったが、これはEnd2Endのモデル。
- YOLO (CVPR 2016)
- SSD (ECCV 2016)
- Mask R-CNN
YOLOはさらにv3、v4、v5と進化する。
R-CNNなどは、画像を切り出す系、
YOLOやSSDは、画像を切り出さない系とされている。
YOLO
「背景である」ことと、「物体である」ことは損失関数の計算として別で計算する
s * s(多くはs=7)のグリッドで画像を区切って、物体の候補領域とそれが何か?を同時に判定
それが何か?はsoftmaxで出力
M2Det
北京大学、アリババ、テンプル大学が共同開発。2019年。
流れ
Backbone Networkと呼ばれる単純な特徴抽出器(VGGやResNet等)で特徴抽出
↓
Multi-Level Feature Pyramid Network(MLFPN)
↓
最終的にPrediction Layerで物体検出および物体認識
Pelee
これも有名なアルゴリズム。
Detctron
Facebook AI Research(FAIR)の物体検出アルゴリズム。オープンソース化されている。
物体検出の評価指標
IoU = Jaccard係数
IoU (Intersection over Union score)
積集合を和集合で割ったもの
完全に重なっていれば1、全く重なっていなければ0
$$ J(A, B) = \frac{|A\cap B|}{|A\cup B|} = \frac{|A \cap B|}{|A| + |B| - |A \cap B|} $$
文字検出で有名なもの
Real-time Scene Text Detection with Differentiable Binarization
PPOCR、TextFuseNet
FOTS(Fast Oriented Text Spotting with a Unified Network)
用語とか補足
-
ILSVRC (The ImageNet Large-Scale Visual Recognition Challenge)
2010年から始まった大規模画像認識の競技会
2015年にはILSVRCの結果で人間の認識性能を超えた。 -
CVPR (Conference on Computer Vision and Pattern Recognition)
アメリカで開催されるコンピュータビジョンに関する世界トップレベルの学会 -
ICCV (International Conference of Computer Vision)
Computer Vision分野では最も権威のある国際会議(トップカンファレンス)の一つ -
CVPR、ECCV、ICCVはComputer Vision分野における世界三大国際会議といわれる。
11 day1とday2の演習
ノートブック
01 基本的なネットワーク
02 改善したネットワーク
03 さらに改善したネットワーク
04 CNNの実装確認






