初心者がKaggle Titanicで上位1.5%(0.83732)以内に入るアプローチ解説_3

前回に続き、Kaggle Titanicで上位1.5%(0.83732)へのアプローチを解説していきます。
使用するコードはGithubのtitanic(0.83732)_3です。
前回に出した提出スコアから、0.83732まで向上させる解説を行います。
###1.必要なライブラリをインポートし、CSVを読み込む。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline,make_pipeline
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectKBest
from sklearn import model_selection
from sklearn.model_selection import GridSearchCV
import warnings
warnings.filterwarnings('ignore')

# CSVを読み込む
train= pd.read_csv("train.csv")
test= pd.read_csv("test.csv")

# データの統合
dataset = pd.concat([train, test], ignore_index = True)

# 提出用に
PassengerId = test['PassengerId']

# 客室階層による生存率比較
dataset['Cabin'] = dataset['Cabin'].fillna('Unknown') # 客室データが欠損している場合はUnknownを代入
dataset['Deck']= dataset['Cabin'].str.get(0) #Cabin（部屋番号）の頭文字（０番目の文字）取得

# チケットの文字数による生存率比較
Ticket_Count = dict(dataset['Ticket'].value_counts()) # チケットの文字数でグループ分け
dataset['TicketGroup'] = dataset['Ticket'].apply(lambda x:Ticket_Count[x]) # グループの振り分け

# チケットの文字数での生存率が高いグループと低いグループの２つに分ける。
# 高ければ２，低ければ１を代入
def Ticket_Label(s):
    if (s >= 2) & (s <= 4): # 文字数での生存率が高いグループ
        return 2
    elif ((s > 4) & (s <= 8)) | (s == 1): # 文字数での生存率が低いグループ
        return 1
    elif (s > 8):
        return 0

dataset['TicketGroup'] = dataset['TicketGroup'].apply(Ticket_Label)

###2.敬称を利用
Kaggle上位者のコードを見ると、名前の敬称を利用することが高スコアのカギだと分かります。
敬称とは、Nameの中間当たりに含まれているMr、Mrs、Missなどのことです。Mrを使わずDr(医師)やRev(聖職者や牧師)といった職業が記載されていることもあります。
これらの情報を抽出してグルーピングします。

# 'Honorifics'(敬称)による特徴別に分ける
dataset['Honorifics'] = dataset['Name'].apply(lambda x:x.split(',')[1].split('.')[0].strip()) #敬称(','と'.'の間の単語)を抽出

# 敬称をグループ分け
# 例：'Capt', 'Col', 'Major', 'Dr', 'Rev'は'Officer'とする
Honorifics_Dict = {}
Honorifics_Dict.update(dict.fromkeys(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
Honorifics_Dict.update(dict.fromkeys(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty'))
Honorifics_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
Honorifics_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
Honorifics_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
Honorifics_Dict.update(dict.fromkeys(['Master','Jonkheer'], 'Master'))
dataset['Honorifics'] = dataset['Honorifics'].map(Honorifics_Dict)
sns.barplot(x="Honorifics", y="Survived", data=dataset, palette='Set3')

"""敬称一覧
Mr：男 , Master：男の子, Jonkheer：オランダ貴族(男),
Mlle：マドモワゼル (フランス未婚女性), Miss：未婚女性、女の子, Mme：マダム(フランス既婚女性), Ms：女性(未婚・既婚問わず), Mrs：既婚女性, 
Don：男(スペイン), Sir：男(イギリス), the Countess：伯爵夫人, Dona：既婚女性(スペイン), Lady：既婚女性(イギリス),
Capt：船長, Col：大佐, Major：軍人, Dr：医者, Rev：聖職者や牧師
"""

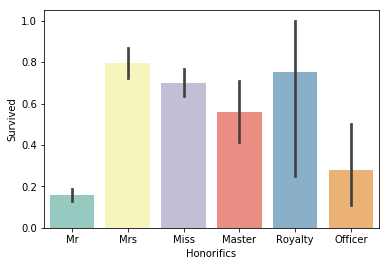
やはり成人男性は生存率が低く、女性や子供が高いです。が、今回、貴族などのRoyaltyグループが子供以上に高いことが発見できます。
この時代の貴族が優先して助かっているのは分かる気がします。
生存率に貴族であるかどうかをデータとして使えるのは武器になりそうです。

###3.欠損値の代入を見直し
前回、前々回は、とりあえず欠損値に中央値を入れました。
予測の精度を上げるにはこれらを見直します。
###3.1 'Age'(年齢)の欠損値の見直し
機械学習で予測したものを年齢の欠損値に代入
予測には先程の敬称(職業)データも使えそうです。（Drで５才といった予測を抑えられる)

## 年齢の欠損値を予測して代入
# 年齢予測のために使う項目を抽出し、ダミー変数を作成
age = dataset[['Age','Pclass','Sex','Honorifics']]
age_dummies = pd.get_dummies(age)
age_dummies.head(3)

# ageが分かるものと欠損しているものに分ける
known_age = age_dummies[age_dummies.Age.notnull()].as_matrix()
null_age = age_dummies[age_dummies.Age.isnull()].as_matrix()

# 特徴量と正解データに分ける
age_X = known_age[:, 1:]
age_y = known_age[:, 0]

# 年齢予測モデルを作成し、予測した値を代入
rf = RandomForestRegressor()
rf.fit(age_X, age_y)
pred_Age = rf.predict(null_age[:, 1:])
dataset.loc[(dataset.Age.isnull()),'Age'] = pred_Age

###3.2 'Embarked'(出港地)の欠損値の見直し
次に'Embarked'(出港地)の欠損値を埋めるために、欠損しているデータを確認します。

# 'Embarked'(出港地)が欠損しているデータを表示
dataset[dataset['Embarked'].isnull()]

どちらも'Pclass'(チケットクラス)が１で、'Fare'(料金)が８０です。
'Pclass'(チケットクラス)が１の、'Embarked'(出港地)ごとの'Fare'(料金)中央値を比較すると、Cが最も近いです。２つの欠損値にはCを代入します。

# 'Pclass'(チケットクラス)が１の、'Embarked'(出港地)ごとの'Fare'(料金)中央値を表示
C = dataset[(dataset['Embarked']=='C') & (dataset['Pclass'] == 1)]['Fare'].median()
print("Cの中央値", C)
S = dataset[(dataset['Embarked']=='S') & (dataset['Pclass'] == 1)]['Fare'].median()
print("Sの中央値", S)
Q = dataset[(dataset['Embarked']=='Q') & (dataset['Pclass'] == 1)]['Fare'].median()
print("Qの中央値", Q)

# 'Embarked'の欠損値にCを代入
dataset['Embarked'] = dataset['Embarked'].fillna('C')

Cの中央値 76.7292
Sの中央値 52.0
Qの中央値 90.0
###3.3 'Fare'(料金)の欠損値の見直し
データを確認すると、'Pclass'(チケットクラス)が3で、'Embarked'(出港地)が'S'だと分かります。
そのため、この欠損値には'Pclass'(チケットクラス)が3で、'Embarked'(出港地)が'S'の中央値を代入します。
これでAge,Embarked, Fareの欠損値を埋められたので確認します。

# 'Fare'(料金)が欠損しているデータを表示
dataset[dataset['Fare'].isnull()]

# 'Pclass'(チケットクラス)が3で、'Embarked'(出港地)が'S'の中央値を代入
fare_median=dataset[(dataset['Embarked'] == "S") & (dataset['Pclass'] == 3)].Fare.median()
dataset['Fare']=dataset['Fare'].fillna(fare_median)

# 全体の欠損データの個数を確認
dataset_null = dataset.fillna(np.nan)
dataset_null.isnull().sum()

Age 0
Cabin 0
Embarked 0
Fare 0
Name 0
Parch 0
PassengerId 0
Pclass 0
Sex 0
SibSp 0
Survived 418
Ticket 0
Deck 0
TicketGroup 0
Honorifics 0
dtype: int64

欠損値がなくなっています。

###4.家族人数
前々回上手く扱えなかった同乗している兄弟/配偶者の数、親/子供の数を使えるデータに加工します
同乗する家族をまとめ、同乗家族の人数による生存率でグループ分けします。

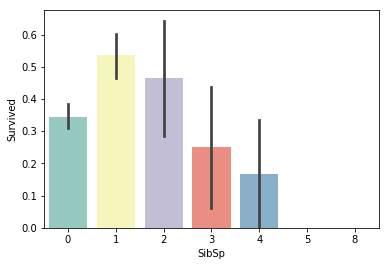
# 同乗している兄弟/配偶者の数による生存率比較
sns.barplot(x="SibSp", y="Survived", data=train, palette='Set3')

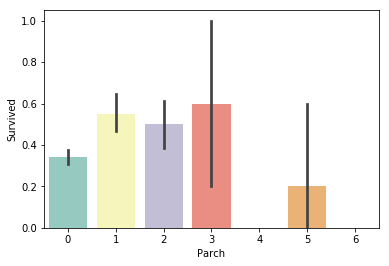
# 同乗している親/子供の数による生存率比較
sns.barplot(x="Parch", y="Survived", data=train, palette='Set3')

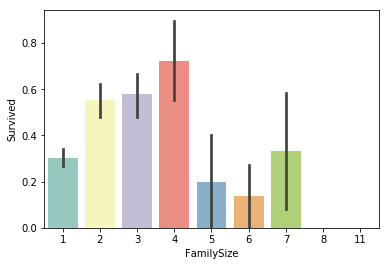
# 同乗している家族の数
dataset['FamilySize']=dataset['SibSp']+dataset['Parch']+1
sns.barplot(x="FamilySize", y="Survived", data=dataset, palette='Set3')

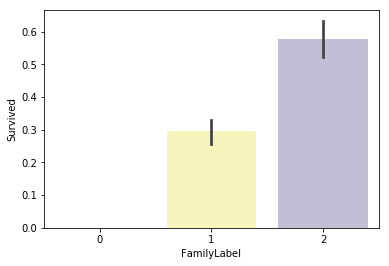
# 家族数による生存率でグループ分け
def Family_label(s):
    if (s >= 2) & (s <= 4):
        return 2
    elif ((s > 4) & (s <= 7)) | (s == 1):
        return 1
    elif (s > 7):
        return 0
dataset['FamilyLabel']=dataset['FamilySize'].apply(Family_label)
sns.barplot(x="FamilyLabel", y="Survived", data=dataset, palette='Set3')

きれいな差に分けることができました。

###5.苗字における生存率調整
上の'SibSp'と'Parch'では３等親以降の家族関係が不明なので、家族でなく苗字における生存率で調査します。
苗字における生存率で大きな差が確認できます。

# 苗字による特徴を調べる
dataset['Surname'] = dataset['Name'].apply(lambda x:x.split(',')[0].strip()) # 苗字(名前の","の前の単語）を抽出
Surname_Count = dict(dataset['Surname'].value_counts()) # 苗字の個数を数える
dataset['Surname_Count'] = dataset['Surname'].apply(lambda x:Surname_Count[x]) # 苗字の個数を代入

# 苗字にダブりがある人を、女・子供のグループと、大人で男性のグループに分ける
Female_Child_Group=dataset.loc[(dataset['Surname_Count']>=2) & ((dataset['Age']<=12) | (dataset['Sex']=='female'))]
Male_Adult_Group=dataset.loc[(dataset['Surname_Count']>=2) & (dataset['Age']>12) & (dataset['Sex']=='male')]

# 女・子供グループにおける苗字ごとの生存率平均の個数を比較
Female_Child_mean = Female_Child_Group.groupby('Surname')['Survived'].mean() # 苗字ごとの生存率平均
Female_Child_mean_count = pd.DataFrame(Female_Child_mean.value_counts()) # 苗字ごとの生存率平均の数
Female_Child_mean_count.columns=['GroupCount']
Female_Child_mean_count

# 男（大人）グループにおける苗字ごとの生存率平均の個数を比較
Male_Adult_mean = Male_Adult_Group.groupby('Surname')['Survived'].mean() # 苗字ごとの生存率平均
Male_Adult_mean_count = pd.DataFrame(Male_Adult_mean.value_counts()) # 苗字ごとの生存率平均の数
Male_Adult_mean_count.columns=['GroupCount']
Male_Adult_mean_count

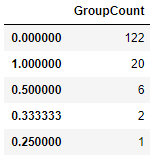
どちらのグループも大抵１か０となり、グループで差が大きく存在することが分かります。
女子供（大人・男）を持つ家族と同じ苗字であれば、全員が生存（死亡）する、というルールでもあるのでしょうか？
これだけはっきりした特徴量は貴重です。
このルールと逆の結果となるものを外れ値として扱うことで、スコアの改善に貢献が期待できます。
何をするかというと、データの書き換えを行います。
女子供（大人・男）を持つ家族と同じ苗字であるのに、全員が死亡（生存）している苗字の人物は、全て逆側のルールに従わせたプロフィールのデータにします。

# 各グループの例外を処理
# 各グループの例外となる苗字を抽出
# Dead_List：女・子供グループで全員死亡した苗字
# Survived_List：男（大人）グループで全員死亡した苗字
Dead_List = set(Female_Child_mean[Female_Child_mean.apply(lambda x:x==0)].index)
print("Dead_List", Dead_List, sep="\n")
Survived_List = set(Male_Adult_mean[Male_Adult_mean.apply(lambda x:x==1)].index)
print("Survived_List", Survived_List, sep="\n")

Dead_List
{'Danbom', 'Turpin', 'Zabour', 'Bourke', 'Olsson', 'Goodwin', 'Cacic', 'Robins', 'Canavan', 'Lobb', 'Palsson', 'Ilmakangas', 'Oreskovic', 'Lefebre', 'Sage', 'Johnston', 'Arnold-Franchi', 'Skoog', 'Attalah', 'Lahtinen', 'Jussila', 'Ford', 'Vander Planke', 'Rosblom', 'Boulos', 'Rice', 'Caram', 'Strom', 'Panula', 'Barbara', 'Van Impe'}
Survived_List
{'Chambers', 'Beane', 'Jonsson', 'Cardeza', 'Dick', 'Bradley', 'Duff Gordon', 'Greenfield', 'Daly', 'Nakid', 'Taylor', 'Frolicher-Stehli', 'Beckwith', 'Kimball', 'Jussila', 'Frauenthal', 'Harder', 'Bishop', 'Goldenberg', 'McCoy'}

# テストデータを書き換える
# データをtrainとtestに分解 
train = dataset.loc[dataset['Survived'].notnull()]
test = dataset.loc[dataset['Survived'].isnull()]

# 女・子供グループで全員死亡した苗字の人→６０歳の男性、敬称はMrに。
# 男（大人）グループで全員生存した苗字の人→５才の女性、敬称はMissに。
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Sex'] = 'male'
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Age'] = 60
test.loc[(test['Surname'].apply(lambda x:x in Dead_List)),'Title'] = 'Mr'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Sex'] = 'female'
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Age'] = 5
test.loc[(test['Surname'].apply(lambda x:x in Survived_List)),'Title'] = 'Miss'

# 再びデータを結合
dataset = pd.concat([train, test])

###6.再び予測を行う

# 使用する変数を抽出
dataset6 = dataset[['Survived','Pclass','Sex','Age','Fare','Embarked','Honorifics','FamilyLabel','Deck','TicketGroup']]
# ダミー変数を作成
dataset_dummies = pd.get_dummies(dataset6)
dataset_dummies.head(3)

# データをtrainとtestに分解 
#（ 'Survived'が存在するのがtrain, しないのがtest ）
train_set = dataset_dummies[dataset_dummies['Survived'].notnull()]
test_set = dataset_dummies[dataset_dummies['Survived'].isnull()]
del test_set["Survived"]

# trainデータを変数と正解に分離
X = train_set.as_matrix()[:, 1:] # Pclass以降の変数
y = train_set.as_matrix()[:, 0] # 正解データ

# 予測モデルの作成
pipe = Pipeline([('classify', RandomForestClassifier(random_state = 10, max_features = 'sqrt'))])

param_test = {'classify__n_estimators':list(range(20, 30, 1)), 
              'classify__max_depth':list(range(3, 10, 1))}
gsearch = GridSearchCV(estimator = pipe, param_grid = param_test, scoring='accuracy', cv=10)
gsearch.fit(X, y)
print(gsearch.best_params_, gsearch.best_score_)

# testデータの予測
predictions = gsearch.predict(test_set)

# Kaggle提出用csvファイルの作成
submission = pd.DataFrame({"PassengerId": PassengerId, "Survived": predictions.astype(np.int32)})
submission.to_csv("submission6.csv", index=False)

'classify__max_depth': 5, 'classify__n_estimators': 28}
0.8451178451178452
提出スコアは0.81818でした。

###7.特徴量を減らして予測
前回に比べて特徴量が２６個と大幅に増えたので、重要でない特徴量を除外します。

pipe = Pipeline([('select',SelectKBest(k=20)),  # 予測に役立つ特徴量を２０個使ってモデルを作成
               ('classify', RandomForestClassifier(random_state = 10, max_features = 'sqrt'))])

param_test = {'classify__n_estimators':list(range(20, 30, 1)), 
              'classify__max_depth':list(range(3, 10, 1))}
gsearch = GridSearchCV(estimator = pipe, param_grid = param_test, scoring='accuracy', cv=10)
gsearch.fit(X, y)
print(gsearch.best_params_, gsearch.best_score_)

{'classify__max_depth': 6, 'classify__n_estimators': 26}
0.8451178451178452

select = SelectKBest(k = 20)
clf = RandomForestClassifier(random_state = 10, warm_start = True, 
                                  n_estimators = 26,
                                  max_depth = 6, 
                                  max_features = 'sqrt')
pipeline = make_pipeline(select, clf)
pipeline.fit(X, y)

先程のモデルとmax_depthとn_estimatorsが変化しました。
このmax_depthとn_estimators情報を用いて、再度特徴量を２０に絞って予測モデルを作成し、予測します。

# 与えられたmax_depthとn_estimatorsを利用して、特徴量を２０に絞って再度予測モデルを作成し、予測
select = SelectKBest(k = 20)
clf = RandomForestClassifier(random_state = 10,
                             warm_start = True, 
                             n_estimators = 26,
                             max_depth = 6, 
                             max_features = 'sqrt')
pipeline = make_pipeline(select, clf)
pipeline.fit(X, y)

cv_score = model_selection.cross_val_score(pipeline, X, y, cv= 10)
print("CV Score : Mean - %.7g | Std - %.7g " % (np.mean(cv_score), np.std(cv_score)))

# testデータの予測
predictions = pipeline.predict(test_set)

# Kaggle提出用csvファイルの作成
submission = pd.DataFrame({"PassengerId": PassengerId, "Survived": predictions.astype(np.int32)})
submission.to_csv("submission7.csv", index=False)

CV Score : Mean - 0.8451402 | Std - 0.03276752
これで提出スコアが0.83732となったはずです。
２０１９年時点での順位は２１７位です。これは上位1.5％に相当します。

###8.まとめ
欠損値を論理的に埋め、敬称など新たに特徴量を生成したり、テストデータの書き換えを行うことで、Kaggle Titanicの上位1.5％に相当する0.83732というスコアを出しました。
様々なデータ加工が出てきており、Titanicがデータ分析力のチュートリアルと扱われているのがよく分かります。

今回でTitanicは一旦終了です。
この記事を拝見した方のお役に立てれば幸いです。