書籍-入門 機械学習による異常検知―Rによる実践ガイド-の7章
「状態空間モデルによる異常検知」で、カルマンフィルタによる異常検知を
実行すると、結果がどうなるのか気になっていました。
そこで、Pythonのnumpyとscipyを使ってゴリゴリ実装してみました。
理論と実装
本稿では、結果の式だけを載せておきます。
式の意味や導出は、書籍をご覧ください。
書籍自体は大変分かりやすく、異常検知を始める人におススメです。
ただ、後半(7章は最後の方)は少し数式が多くなり、難しくなってきます。
データロード
書籍でも使われている心拍数のデータを使います。
import urllib.request
import numpy as np
from numpy.linalg import svd, inv, matrix_rank
import matplotlib.pyplot as plt
from scipy.linalg import sqrtm
url = "http://www.cs.ucr.edu/~eamonn/discords/qtdbsel102.txt"
f_name = "data.txt"
# ダウンロードを実行
urllib.request.urlretrieve(url, f_name)
# データ抽出
data = np.loadtxt(f_name, delimiter="\t")
data = data[2000:5000,1]
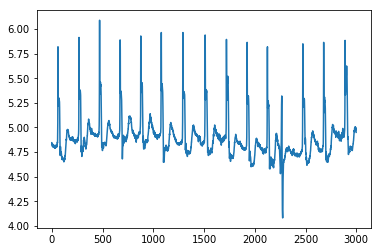
plt.plot(data)
plt.show()
このデータは長い時系列のデータとなっていますが、ここでは
時間:2000~5000(3000個)のデータを使います。
データ作成
$X_p,X_f$を作ります。
$X_p$は時間的に前のデータを格納した行列、$X_f$は後のデータを格納した行列です。
w = 50 # 抽出窓の幅
m = 2 # zの次元
T = 1000 # 学習区間
x, x_after = [], []
for i in range(w, T):
x.append(data[i-w: i])
x_after.append(data[i: i+w])
x_p = np.array(x).T
x_f = np.array(x_after).T
カルマンフィルタ
異常検知で使うカルマンフィルタは以下の式で定義されます。
\begin{align}
p(x^{(t)}|z^{(t)}) &=N(x^{(t)}|Cz^{(t)},R) \\
p(z^{(t)}|z^{(t-1)}) &=N(z^{(t)}|Az^{(t-1)},Q)
\end{align}
制御などで使うカルマンフィルタとはちょっと形が違います。
ただし、xは観測値を表すベクトル、zは内部状態を表すベクトル、Rは観測値のばらつきを表す共分散行列、Qは内部状態のばらつきを表す共分散行列です。状態変数系列のzを更新しながら、異常検知を行います。
行列A,C,Q,Rは部分空間同定法で求めます。
部分空間同定法
カルマンフィルタで使うA,Q,C,Rを部分空間同定法で求めます。
まずは、Wを求めます。
\begin{align}
S_{pf}=X_pX_f^T\\
S_{pp}=X_pX_p^T\\
S_{ff}=X_fX_p^T
\end{align}
W=S_{pp}^{-1/2}S_{pf}S_{ff}^{-1/2}
$X^{-1/2}$は$X^{1/2}$の逆行列を表します。
s_pf = x_p @ x_f.T
s_pp = x_p @ x_p.T
s_ff = x_f @ x_f.T
# 行列W
W = inv(sqrtm(s_pp)) @ s_pf @ inv(sqrtm(s_ff))
次に、Wについて特異値を求めます。
そして、特異値が大きい順にm本の左右特異ベクトルを求めます。
# 左右特異ベクトル
left, _, right = svd(W)
左特異ベクトルを特異値の大きい順に$\tilde{\alpha}^1,...,\tilde{\alpha}^m$、
右特異ベクトルを特異値の大きい順に$\tilde{\beta}^1,...,\tilde{\beta}^m$とし、$\tilde{\alpha}^i$、$\tilde{\beta}^i$を求めます。
\begin{align}
\alpha^i=S_{pp}^{-1/2}\tilde{\alpha}^i\\
\beta^i=S_{ff}^{-1/2}\tilde{\beta}^i\\
\end{align}
# 特異ベクトルm本抽出
alpha, beta = [], []
for i in range(m):
alpha.append(inv(sqrtm(s_pp)) @ left[:,i])
beta.append(inv(sqrtm(s_ff)) @ right[i,:])
次に$\hat{Z}_p$ , $\hat{Z}_f$を求めます。
\begin{align}
\hat{Z}_p=[\alpha^1,...,\alpha^m]^TX_p\\
\hat{Z}_f=[\beta^1,...,\beta^m]^TX_f\\
\end{align}
# zを算出
z_p = np.array(alpha) @ x_p
z_f = np.array(beta) @ x_f
$\omega$を検出窓の大きさとして、以下の値を求めます。
\begin{align}
X &=[x^{(1)}, ...,x^{(T-w)}]\\
Z &=[z^{(1)}, ...,z^{(T-w)}]\\
Z_+ &=[z^{(2)}, ...,z^{(T-w)}]\\
Z_- &=[z^{(1)}, ...,x^{(T-w-1)}]
\end{align}
最後にA,Q,C,Rを求めます。
\begin{align}
A &=(Z_+Z_-^T)(Z_-Z_-^T)^{-1}\\
Q &=\frac{1}{T-w-1}(Z_+-AZ_-)(Z_+-AZ_-)^T\\
C &=(XZ^T)(ZZ^T)^{-1}\\
R &=\frac{1}{T-w}(X-CZ)(X-CZ)^T
\end{align}
# A, Q, C, R
X = np.copy(x_p)
Z = np.copy(z_p)
Z_plus = z_p[:,1:]
Z_minus = z_p[:,:-1]
A = (Z_plus @ Z_minus.T) @ inv(Z_minus @ Z_minus.T)
Q = ((Z_plus - A @ Z_minus) @ (Z_plus - A @ Z_minus).T)/(T-w-1)
C = (X @ Z.T) @ inv(Z @ Z.T)
R = ((X - C @ Z) @ (X - C @ Z).T)/(T-w)
漸化式
$z^{(t-1)}$を以下の式で置き換え、
p(z^{(t-1)}|X_{t-1}) = N(z^{(t-1)}|\mu_{t-1},V_{t-1})
次の漸化式で$\mu_t,Q_t$を推定します。
\begin{align}
K_t &= Q_{t-1}C^T(R+CQ_{t-1}C^T)^{-1}\\
\mu_t &= A\mu_{t-1}+K_t(x^{(t)}-CA\mu_{t-1})\\
V_t &= (I_m-K_tC)Q_{t-1}\\
Q_t &= Q+AV_tA^T
\end{align}
def update(A, Q, C, R, q, x, mu, m):
k_t = q @ C.T @ inv(R + C @ q @ C.T)
mu_t = A @ mu + k_t @ (x - C @ A @ mu)
v_t = (np.eye(m) - k_t @ C) @ q
q_t = q + A @ v_t @ A.T
return mu_t, q_t
ただし、$\mu_0,Q_0$の初期値は適当に与えます。
q = np.eye(m)
mu = np.zeros(m)
異常値
異常値aは以下の式で定義されます。
\begin{align}
a(x^{(t)}) &=(x^{(t)}-CA\mu_{t-1})^T\Sigma_t^{-1}(x^{(t)}-CA\mu_{t-1})\\
\Sigma_t &=R+CQ_{t-1}C^T
\end{align}
def anomaly_score(A, C, R, q, x, mu):
sigma = R + C @ q @ C.T
predict = C @ A @ mu
score = (x - predict).T @ sigma @ (x - predict)
return [score, predict, sigma]
結果
最後に異常検知を行います。
result_score, result_predict, result_sigma = [], [], []
begin = 950
end = 1000
for i in range(2000):
# t-1
x = data[begin + i: end + i]
mu, q = update(A, Q, C, R, q, x, mu, m)
# t
x = data[begin + i + 1: end + i + 1]
result = anomaly_score(A, C, R, q, x, mu)
result_score.append(result[0])
result_predict.append(result[1])
sigma_predict = np.array(result[2])
sigma_predict = sigma_predict[-1, -1] - sigma_predict[-1,:-1] @ inv(sigma_predict[:-1,:-1]) @ sigma_predict[-1,:-1].T
result_sigma.append(np.max([sigma_predict, 0]))
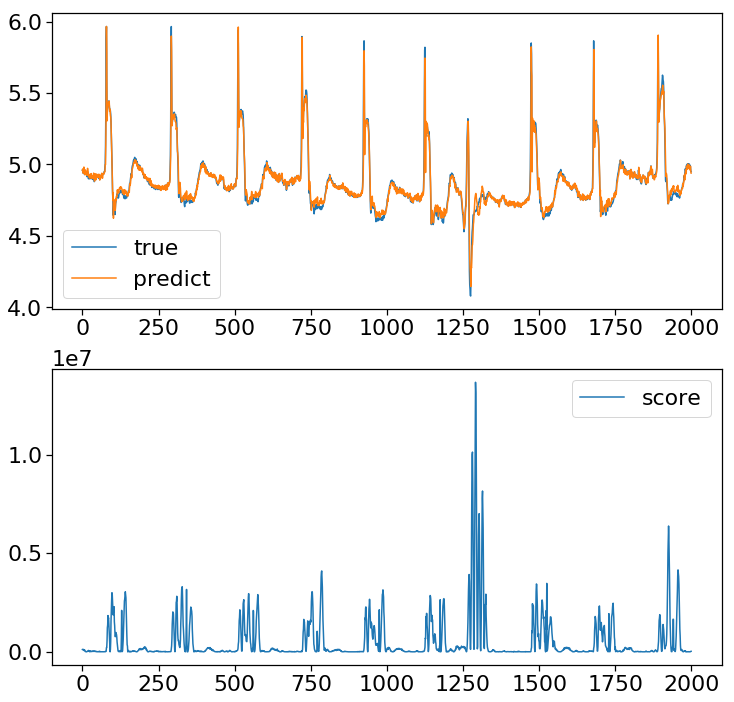
グラフを表示します。
result_score = np.array(result_score)
result_predict = np.array(result_predict)
result_sigma = np.array(result_sigma)
# boundary_upper = result_predict[:,-1] + 2*np.sqrt(result_sigma)
# boundary_lower = result_predict[:,-1] - 2*np.sqrt(result_sigma)
plt.figure(figsize=(12,12))
plt.subplot(2,1,1)
plt.plot(data[1000:3000], label="true")
# plt.fill_between(np.arange(2000), boundary_upper, boundary_lower, facecolor='y',alpha=0.3)
plt.plot(result_predict[:,-1], label ="predict")
# plt.xlim(1300,1400)
plt.legend()
plt.subplot(2,1,2)
plt.plot(result_score, label="score")
# plt.xlim(1300,1400)
plt.legend()
plt.show()
ちゃんと異常検知できましたが、K近傍法と同じような感度かなぁという印象。
やはり目的は違いますが、特異スペクトル変換(書籍参照)の方が感度良く検知します。