ローカルレベルモデルを用いた時系列データに対する異常検知

#やったこと
入門 機械学習による異常検知―Rによる実践ガイドを読み進めていくと、7.4に「状態空間モデルによる異常検知」がありますが、こちらではＲを使った実装がなされていませんでした。そこで、状態空間モデルの簡易版？のローカルレベルモデルを用いて実装してみました。

なお、カルマンフィルタを使ったローカルレベルモデルを一から実装してみたかったこともあり、時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装を参考にしながら、Pythonに置きなおした形で実装してみました。

こちらの産業機械の異常状態をローカルレベルモデルを使って検知してみたに応用事例を初会しています。

#ライブラリ

#基本ライブラリ
import numpy as np
import pandas as pd

#図形描画ライブラリ
import matplotlib.pyplot as plt
plt.style.use('seaborn-darkgrid')
from matplotlib.pylab import rcParams

# 統計モデル（最尤推定で使用）
from scipy.optimize import minimize

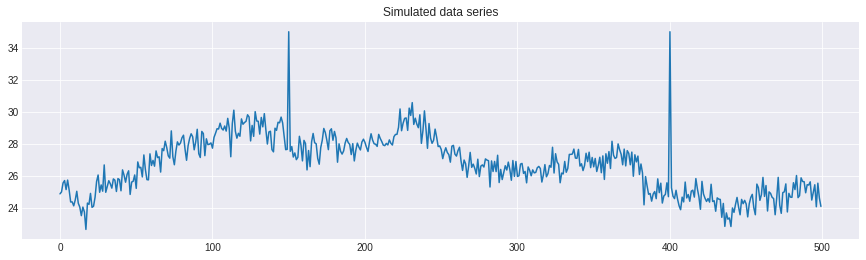
#シミュレーションデータ

#サンプルサイズ
N = 500

#乱数固定
np.random.seed(500)

#状態方程式
mu = np.cumsum(np.random.normal(loc=0, scale=0.2, size=N)) + 25

#観測値
obs = mu + np.random.normal(loc=0, scale=0.5, size=N)

#異常値
obs[150] = 35
obs[400] = 35

rcParams['figure.figsize'] = 15,4
plt.plot(obs)
plt.title('Simulated data series')
plt.show()

#モデル
入門 機械学習による異常検知―Rによる実践ガイドによると、線形状態空間モデルは以下の式が成り立つモデルです。

\begin{align}
    p(x^{(t)}|z^{(t)}) &=N(x^{(t)}|Cz^{(t)},R) \\
    p(z^{(t)}|z^{(t-1)}) &=N(z^{(t)}|Az^{(t-1)},Q)
\end{align}

ここでxは観測値を表すベクトル、zは内部状態を表すベクトル、Rは観測値のばらつきを表す共分散行列、Qは内部状態のばらつきを表す共分散行列です。推定するのは、状態変数系列のzと、未知のパラメータA,C,Q,Rです。
また、異常値の検知は以下の式で定義が可能です。

\begin{align}
    a(x^{(t)}) &=(x^{(t)}-CA\mu_{t-1})^T\Sigma_t^{-1}(x^{(t)}-CA\mu_{t-1})\\
   \Sigma_t^{-1} &=R+CQ_{t-1}C^T
\end{align}

私の理解では、ローカルレベルモデルはA=C=1だと考えていますが、間違っていたら教えてください！

#関数の定義
最初に書いた通り、時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装を大いに参考にさせてもらいました。

#データ（numpyのarrayにすること）
data_series = np.array(obs)

def Kf_LocalLevel(y, mu_pre, P_pre, sigma_w, sigma_v):
  #step1: forecast
  mu_forecast = mu_pre
  P_forecast = P_pre + sigma_w
  y_forecast = mu_forecast
  F = P_forecast + sigma_v
  
  #step2: filtering
  K = P_forecast / (P_forecast + sigma_v)
  y_residual = y - y_forecast
  mu_filter = mu_forecast + K * y_residual
  P_filter = (1-K) * P_forecast
  
  #store the result
  result = {
      'mu_filter' : mu_filter,
      'P_filter' : P_filter,
      'y_residual' : y_residual,
      'F' : F,
      'K' : K
  }
  
  return result



def cal_LogLik_LocalLevel(sigma,data_series=data_series):
  data_series = np.array(data_series)
  
  sigma_w = np.exp(sigma[0])
  sigma_v = np.exp(sigma[1])

  #sample size
  N = len(data_series)

  #状態の推定量
  mu_zero = 0
  mu_filter = np.hstack((mu_zero,np.zeros(N)))

  P_zero = 10000000
  P_filter = np.hstack((P_zero,np.zeros(N)))

  #
  y_residual =  np.zeros(N)
  F =  np.zeros(N)
  K =  np.zeros(N)

  for i in range(0,N):
    result = Kf_LocalLevel(y=data_series[i], 
                           mu_pre=mu_filter[i], 
                           P_pre=P_filter[i],
                           sigma_w=sigma_w, 
                           sigma_v=sigma_v)
    mu_filter[i+1] = result['mu_filter']
    P_filter[i+1] = result['P_filter']
    y_residual[i] = result['y_residual']
    F[i] = result['F']
    K[i] = result['K']

  LogLik = 1/2 * np.sum( np.log(F) + y_residual**2 / F )
  
  return LogLik



def output_sigma(initial_value=list((1,1))):
  opt_result = minimize(fun=cal_LogLik_LocalLevel, x0=initial_value, method='l-bfgs-b')
  
  return np.exp(opt_result.x)



def smooth_LocalLevel(mu_filtered, P_filtered, r_post, s_post, F_post, y_residual_post, K_post):
  r = y_residual_post / F_post + (1-K_post) * r_post
  mu_smooth = mu_filtered + P_filtered * r
  
  s = 1/F_post + (1-K_post)**2 * s_post
  P_smooth = P_filtered - P_filtered**2 * s

  
  #store the result
  result = {
      'mu_smooth' : mu_smooth,
      'P_smooth' : P_smooth,
      'r' : r,
      's' : s
  }
  
  return result

#パラメータ等の推定

#----------過程誤差と観測誤差の推定----------#

#サンプルサイズ
N = len(data_series)

#状態の推定量
mu_zero = 0
mu_filter = np.hstack((mu_zero,np.zeros(N)))

#状態の分散
P_zero = 10000000
P_filter = np.hstack((P_zero,np.zeros(N)))

#観測値の予測残差
y_residual =  np.zeros(N)

#観測値の予測残差の分散
F =  np.zeros(N)

#カルマンゲイン
K =  np.zeros(N)

#過程誤差の分散
sigma_w = 1000

#観測誤差の分散
sigma_v = 10000


#最尤推定
print(output_sigma())

#過程誤差の最適な分散
sigma_w = output_sigma()[0]

#観測誤差の最適な分散
sigma_v = output_sigma()[1]



#----------状態の推定----------#
for i in range(0,N):
  result = Kf_LocalLevel(y=data_series[i],
                         mu_pre=mu_filter[i],
                         P_pre=P_filter[i],
                         sigma_w=sigma_w,
                         sigma_v=sigma_v)
  mu_filter[i+1] = result['mu_filter']
  P_filter[i+1] = result['P_filter']
  y_residual[i] = result['y_residual']
  F[i] = result['F']
  K[i] = result['K']


  
#----------平準化----------#
# 平滑化状態
mu_smooth = np.zeros(N + 1)

# 平滑化状態分散
P_smooth = np.zeros(N + 1)

# 漸化式のパラメタ（初期値は0のままでよい）
r = np.zeros(N)
s = np.zeros(N)

# 最後のデータは、フィルタリングの結果とスムージングの結果が一致する
mu_smooth[-1] = mu_filter[-1]
P_smooth[-1] = P_filter[-1]

# 逆順でループ
for i in range(N-1,-1,-1):
  result = smooth_LocalLevel(
    mu_filter[i],P_filter[i],r[i], s[i], F[i], y_residual[i], K[i]
  )
  mu_smooth[i] = result['mu_smooth']
  P_smooth[i] = result['P_smooth']
  r[i - 1] = result['r']
  s[i - 1] = result['s']

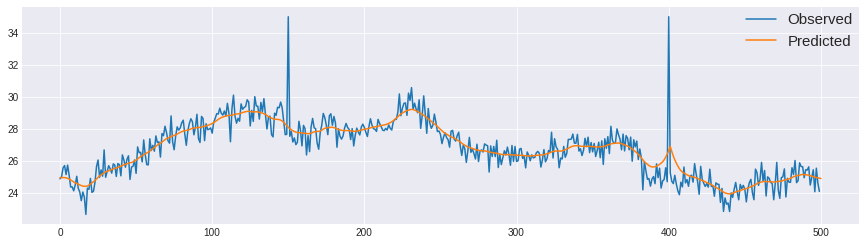
plt.plot(obs, label='Observed')
plt.plot(mu_smooth, label='Predicted')
plt.legend(loc='upper right', borderaxespad=0, fontsize=15)

#異常値の検知
上記の説明では以下の式で異常値検知の式が与えられると書きましたが、

\begin{align}
    a(x^{(t)}) &=(x^{(t)}-CA\mu_{t-1})^T\Sigma_t^{-1}(x^{(t)}-CA\mu_{t-1})\\
   \Sigma_t^{-1} &=R+CQ_{t-1}C^T
\end{align}

ローカルレベルモデルはA=C=1であり、今回の観測値は1×mベクトルになるので、要するに、

\begin{align}
    a(x^{(t)}) &=(x^{(t)}-\mu_{t-1})\sigma_t\\
   \sigma_t &=R+Q
\end{align}

という、状態と観測の分散を足したものに、観測値と状態値を引いたものを掛け合わせるということになります（直感的には自然ですが、当たり前すぎて理解があってるのか謎です…？）。

sigma = P_smooth[1:] + F

anomaly_detection = np.zeros(N-1)

for i in range(1,N-1):
  anomaly_detection[i] = (obs[i] - mu_smooth[i-1])*sigma[i]
  
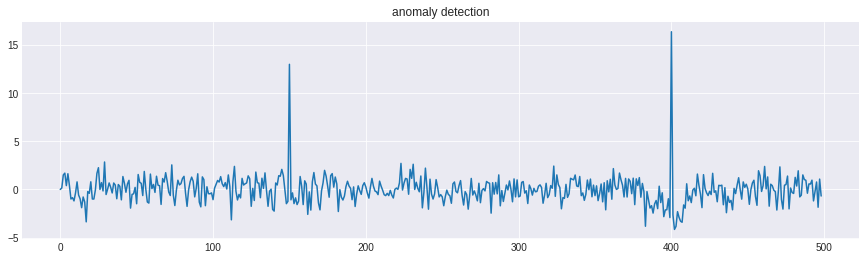
plt.plot(anomaly_detection)
plt.title('anomaly detection')

150と400でスパイクしているので、この2ヵ所で異常が生じているということが分かります。

#参考文献

時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装 [単行本]

馬場 真哉

プレアデス出版

2018-02-14

入門 機械学習による異常検知―Rによる実践ガイド [単行本]

井手 剛

コロナ社

2015-02-19