LoginSignup
57
33

More than 5 years have passed since last update.

NTTドコモ サービスイノベーション部Advent Calendar 2018Day 22nttdocomo_service_innovation
@shin_ishiguro(Shin Ishiguro)inNTTドコモ サービスイノベーション部

BigQuery GISを用いた位置情報データ分析の入門

Posted at

イントロダクション

こんにちは、はじめまして。ドコモの石黒慎と申します。

私は位置情報に関するデータ分析を主に行っています。対象としているのはドコモの携帯電話ユーザーの位置情報を統計化したモバイル空間統計のデータを用いた大規模な人口・人流データの分析に基づいた交通の最適化です。

具体的には、AIタクシーというタクシー需要予測プロジェクトや、ドコモ・バイクシェアの自転車再配置の最適化といったプロジェクトの研究をしています。

大規模な人流データを扱うための前処理として空間データベースを利用することが多いです。例えばPostGISとQGISを組み合わせた位置情報データの前処理・可視化などです。

最近は、GoogleからリリースされたBigQuery GISの機能に注目しています。

そこで今回の記事では、BigQuery GISの機能紹介を行なった後、簡単な位置情報分析をエンジョイしてみたいと思います。

もし興味ございましたら、ぜひ記事の最後までお付き合いくださると幸いです。

本記事の目標：読者にお持ち帰りいただきたいもの

  • 空間DBの基本概念
  • BigQuery GISの現時点における全関数の説明
  • NYCタクシーデータを用いたGeo Vizによる簡単な位置情報の可視化

空間DBが使えると何が嬉しいのか？

まずは、位置情報データ分析に馴染みのない方向けに、空間DBの必要性について説明させていただきます。

位置情報データは緯度・経度（稀に高度や精度も）を含んだ幾何情報データです。

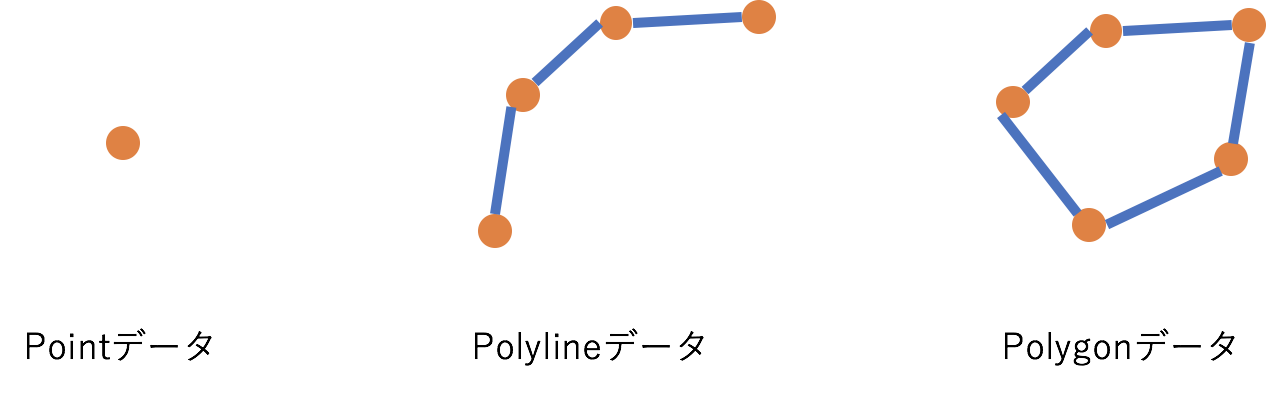
幾何情報は頂点の集合、ポリゴンデータの形で記録されています。データ型としては、大きくは頂点(Point)データ、曲線(PolyLine)データ、面(Polygon)データの３種類とそれらが複数内包された集合データが存在しています。

image-20181222073356575.png

空間DBは、複数のポリゴン同士の位置関係の高速計算を実現するものです。空間DBではR-treeという木構造を利用することで空間インデックスを作成し、位置情報の計算を効率化します。

R-treeでは、頂点の集合に外接するバウンディングボックスで頂点群を近似し、簡単な形状に変換します。頂点の集合が複数個あれば、グループ化をしていくことで木構造を形成します。

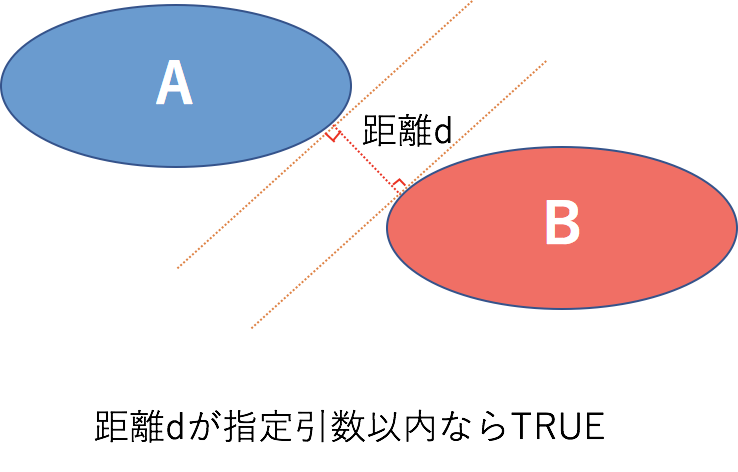
R-treeを使えば、ポリゴン同士の位置関係の計算はバウンディングボックスの位置関係の計算に近似することができるので、計算量を大幅に削減することが可能となります。位置情報でよく用いられる包含関係や距離の計算の際に非常に有効です。

R-treeによる空間インデックスは木構造であることから、データベースと相性が良いです。このため空間DBにはR-treeのデータ構造が採用されています。

計算量の削減は、位置情報データが大規模になればなるほど重要です。したがって、テラバイト級（ときにはペタバイト級も）のデータを扱うドコモの位置情報データ分析でも空間DBが非常に役に立っています。

image-20181222075218765.png

BigQuery GISのファンクション総覧

BigQuery GISはBigQueryに空間DBの機能を導入したものです。

BigQuery GISによって、BigQuery上で様々な位置情報の分析・可視化が可能となりました。特にGoogle Geo Vizによる可視化機能が便利で、GCPで完結して簡単にGoogle Mapに位置情報分析の結果を可視化できるようになっています。

それでは、BigQuery GISの全機能を概観してみましょう。

  • BigQuery GISの仕様について

    • 現状、測地系はWGS84のみに対応しているようです
    • デフォルトでは距離計算はsphere (球)で行われます
    • spheroidの引数を持つ関数のみ、spheroid=TRUEを指定することでWGS84の測地系を考慮した楕円曲面でより精度高く距離計算が行われます。（ただし、精度向上は速度とのトレードオフとなります）

  • ST_GEOGPOINT

    • ST_GEOGPOINT(longitude, latitude)
    • longitude = 経度、latitude = 緯度を受け取って、一つのpoint = 頂点となるGEOGRAPHYを生成し返却します
    • 緯度経度はFLOAT64型で与えられます
    • latitudeは[-90, 90]の範囲で与えられます
    • longitudeは[-180, 180]の範囲で与えられ、範囲外となる入力が与えられる場合は360の剰余が算出され、[-180, 180]の範囲に変換されます
    • image-20181202003151788.png

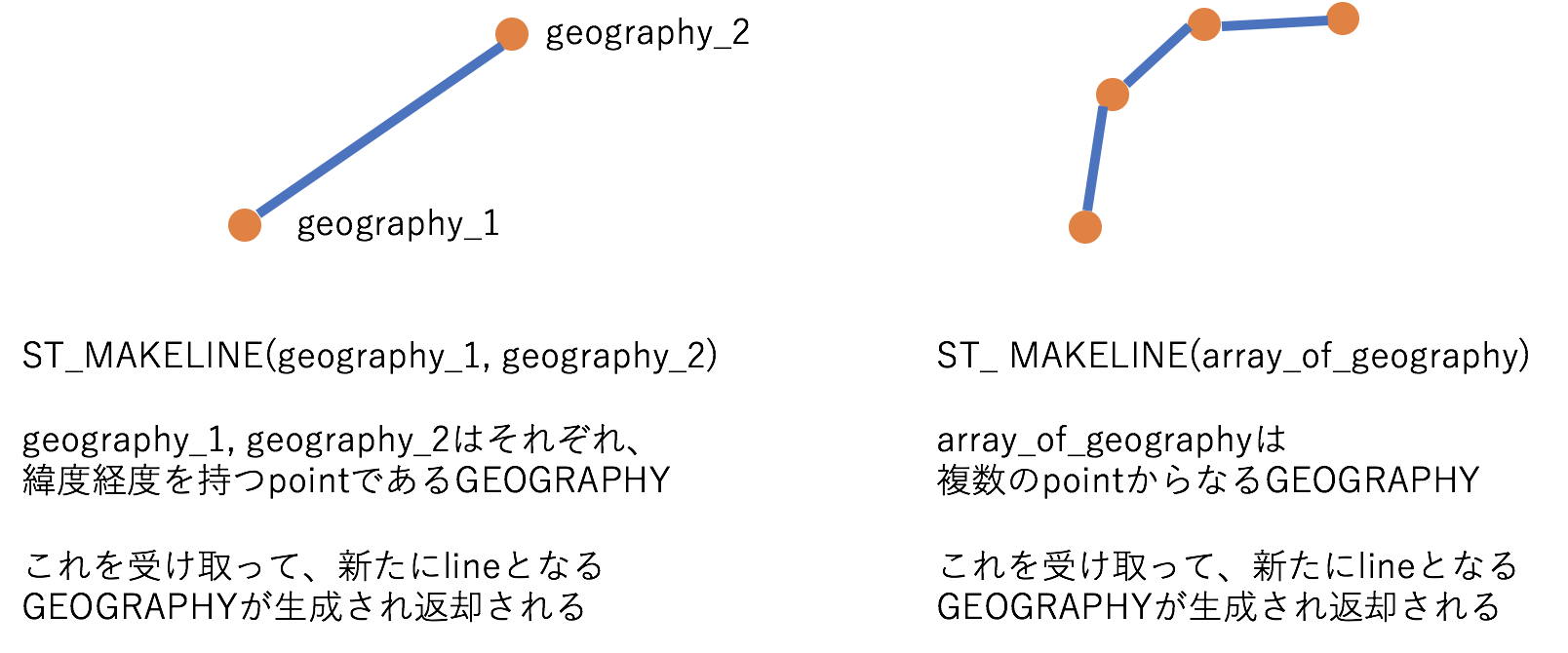
  • ST_MAKELINE

    • ST_MAKELINE(geography_1, geography_2)
    • ST_MAKELINE(array_of_geography)
    • 二つのpointまたは複数のpointからなるlineを生成する
    • image-20181202003752431.png

  • ST_MAKEPOLYGON

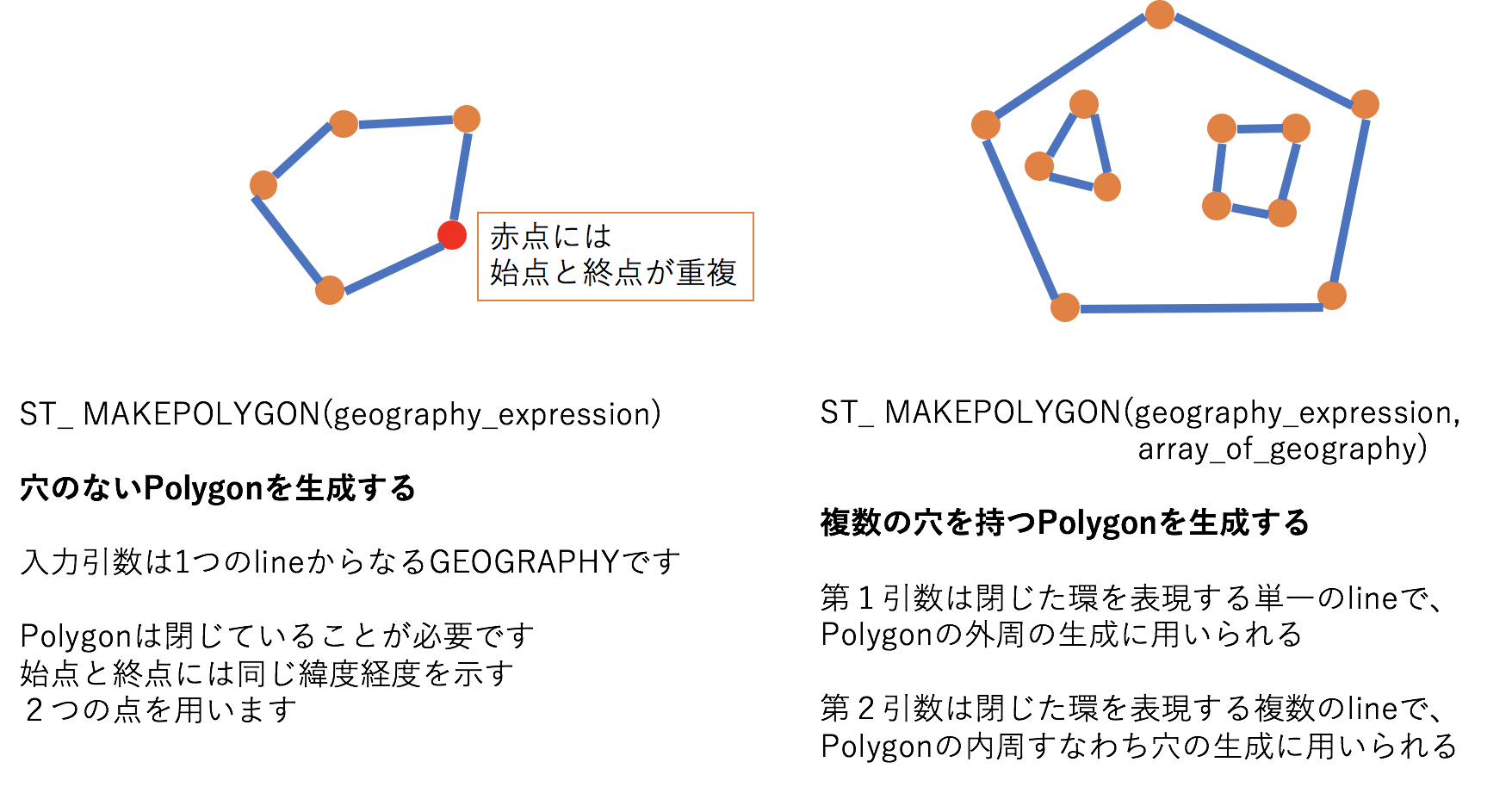
    • ST_MAKEPOLYGON(geography_expression)
    • ST_MAKEPOLYGON(geography_expression, array_of_geography)
    • 一つのlineを入力とし、ポリゴンを生成します
    • ポリゴンは閉じている必要があり、初めの頂点と最後の頂点の緯度経度が等しいことが必須です
    • polygonの入力となるlineは3点の異なる座標を持つことが必要です
    • また、複数の穴を持つトポロジーから構成されるPolygonを生成することも可能です
    • その場合は、第１引数に外周の単一のlineを、第２引数に穴を表現する内周の複数のlineを指定します
    • 外周のポリゴンは内周の穴となるポリゴンを内包することが必須です
    • 外周は1つであり、ポリゴンの穴をネストすることはできません
    • 外周と内周の全ての環はそれぞれの境界線で点接触しても良いです
      • 境界線そのものを共有すると形状が変わってしまうのでNGです
    • NOTE: 入力のlineをemptyで設定することも可能で、その場合は地球全体を覆うPolygonが生成されます
    • NOTE: BigQueryのsnappingプロセスは極めて短いエッジの削除を実施します。このため、polygonの穴が消去されることがあります
    • image-20181202010358313.png

  • ST_MAKEPOLYGONORIGIENTED

    • ST_MAKEPOLYGONORIENTED(array_of_geography)
    • ST_MAKEPOLYGONに類似する機能を持つが、頂点の順序に従ってポリゴンが生成される
    • 配列の一つ目のポリゴンが外環を形成する

  • ST_GEOGFROMGEOJSON

    • ST_GEOGFROMGEOJSON(geojson_string)
    • GeoJSONと呼ばれるGeometryデータをJSON形式で表現したデータからGeometryデータを読み込みます

  • ST_GEOGFROMTEXT

    • ST_GEOGFROMTEXT(wkt_string [, oriented=FALSE])
    • WKT = Well Known Textと呼ばれる形式のテキストデータからGeometryデータを読み込みます

  • ST_GEOGFROMWKB

    • ST_GEOGFROMWKB(wkb_bytes)
    • Well Known Binaryと呼ばれる形式の16進数バイナリデータからなるGeometryデータを読み込みます

  • ST_ASGEOJSON

    • ST_ASGEOJSON(geography_expression)
    • GeoJSONとしてGeometryデータを書き出します
    • GeoJSONはWebアプリなどでよく使われている形式です。
    • GeoJSONに変換すると、例えばJupyter上でデータを読み込んで地図に可視化することができます。

  • ST_ASTEXT

    • ST_ASTEXT(geography_expression)
    • GeometryデータをWKT形式のテキストデータに変換します
    • WKTのテキストデータは人間にも読み書きできる形式です
    • 「緯度経度x, yの頂点データ」のような形式で書かれています
    • テキストデータである分、バイナリに比べて容量は大きいです

  • ST_ASBINARY

    • ST_ASBINARY(geography_expression)
    • GeometryデータをWKB形式のバイナリデータに変換します
    • 大容量のデータを保管したり、転送するにはバイナリ形式が便利です

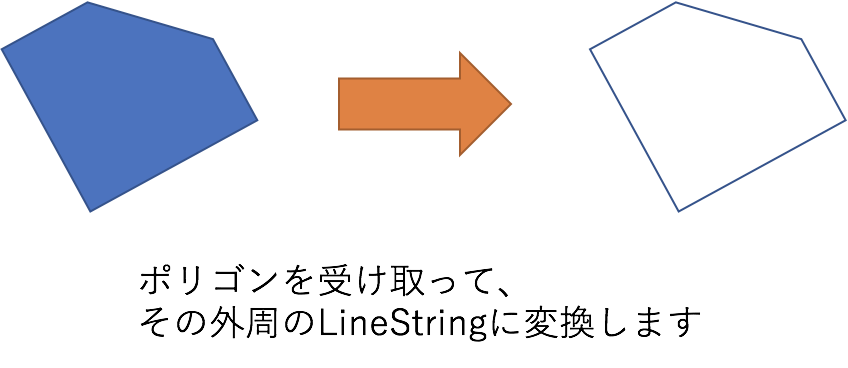
  • ST_BOUNDARY

    • ST_BOUNDARY(geography_expression)
    • ジオメトリの境界となるジオメトリを生成します
    • Polygonを入力とすると、そのPolygonの内周を構成するLinestringが返ります
    • 複数の穴を含むトポロジーからなるPolygonであれば、その全ての内周を返却します
    • image-20181222085047486.png

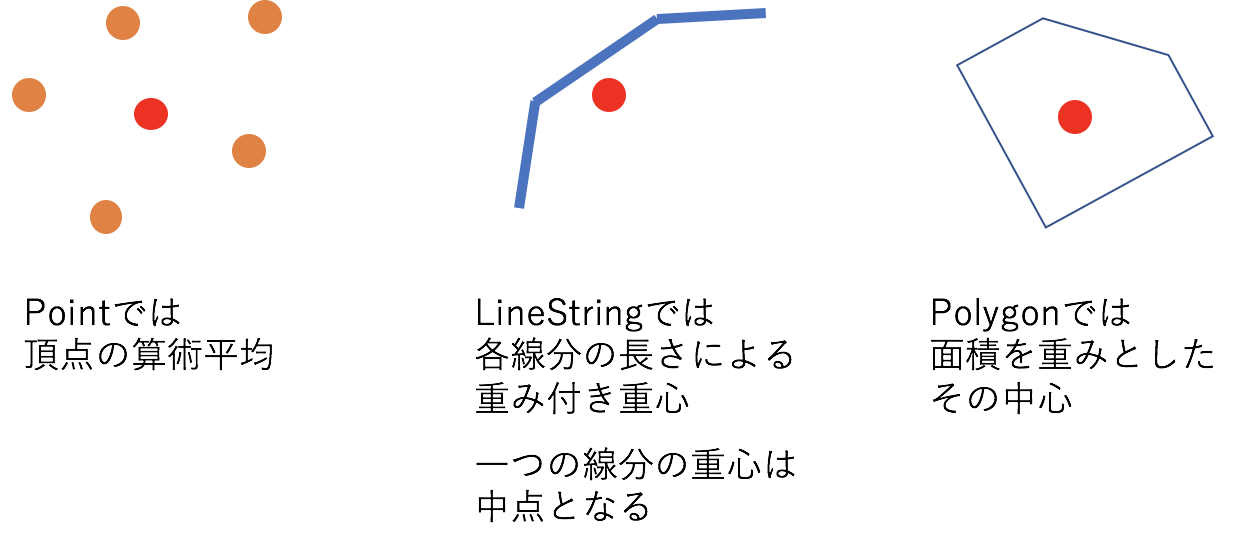
  • ST_CENTROID

    • ST_CENTROID(geography_expression)
    • 重心となる頂点のジオメトリを返却します
    • Collectionが入力された場合は内包されるジオメトリの内、最大の次元に該当する各ジオメトリの重心の重み付き平均を計算する
    • image-20181222090545020.png
    • ST_CLOSESTPOINT(geography_1, geography_2)
    • の形で使い、geography_1を構成する幾何構造のうち、最も近い頂点を返却します
    • image-20181222092842493.png

  • ST_DIFFERENCE

    • ST_DIFFERENCE(geography_1, geography_2)
    • の形で使い、二つのジオメトリを構成する頂点を調べ、異なる頂点の集合を返却します
    • つまり $ (A \cup B) \cap ( A \cap \lnot B) $ を返します
    • image-20181222093212536.png

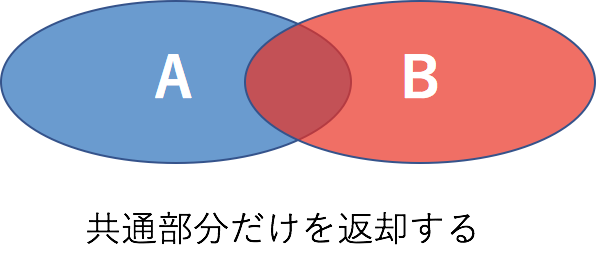
  • ST_INTERSECTION

    • ST_INTERSECTION(geography_1, geography_2)
    • の形で使い、二つのジオメトリを構成する頂点を調べ、共通する頂点の集合を返却します
    • つまり $ (A \cap B) $ を返却します
    • image-20181222093651696.png

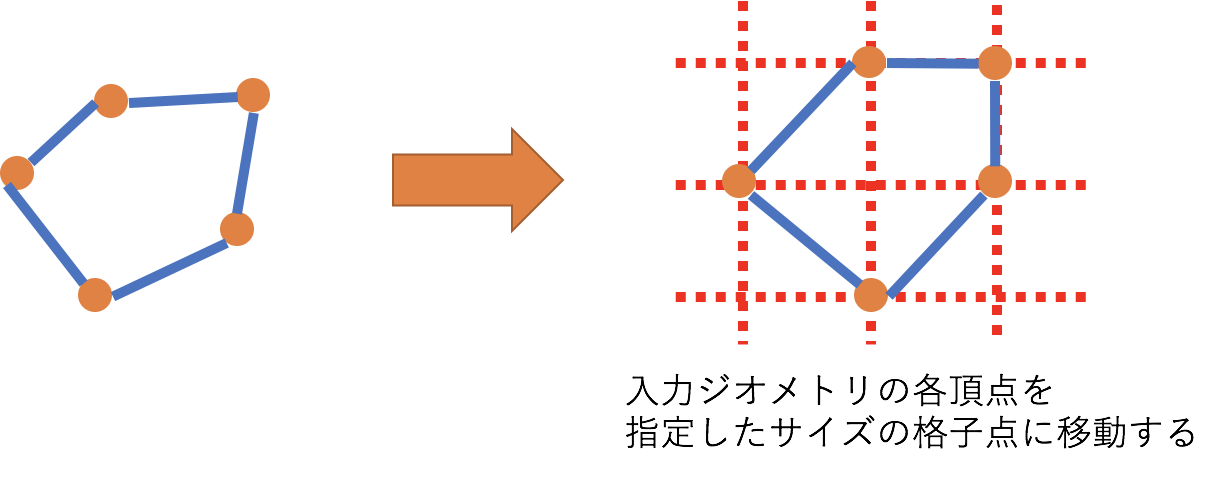
  • ST_SNAPTOGRID

    • ST_SNAPTOGRID(geography_expression, grid_size)
    • 入力となるジオメトリの各頂点をgridに転写します
    • 第２引数でグリッドサイズを指定する
    • ジオメトリの点の数を減らし、精度を落とすために使います
    • image-20181222094805909.png

  • ST_UNION

    • ST_UNION(geography_1, geography_2)
    • ST_UNION(array_of_geography)
    • 複数のGEOGRAPHYを入力とし、GEOGRAPHYの和集合を返却します
    • つまり $ (A \cup B) $ となるGEOGRAPHYを返却します
    • 入力には、２つのGEOGRAPHYまたはGEOGRAPHYの配列のどちらかが使えます
    • ST_UNION_AGGはST_UNIONのaggregateバージョンです
    • image-20181202002304670.png

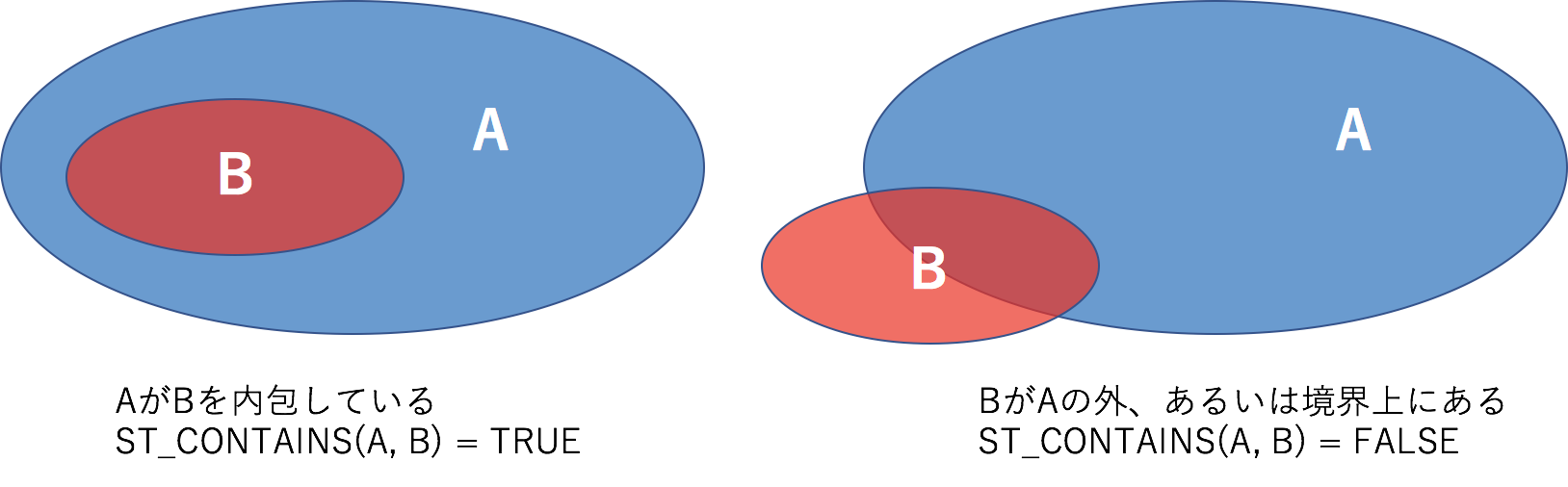
  • ST_CONTAINS

    • ST_CONTAINS(geography_1, geography_2)
    • AがBを完全に内包していたらTRUEが返却されます
    • BがAの外に、はみ出していたらFALSEが返却されます
    • BがAの境界上にあったら、FALSEが返却されます
    • image-20181222095512933.png

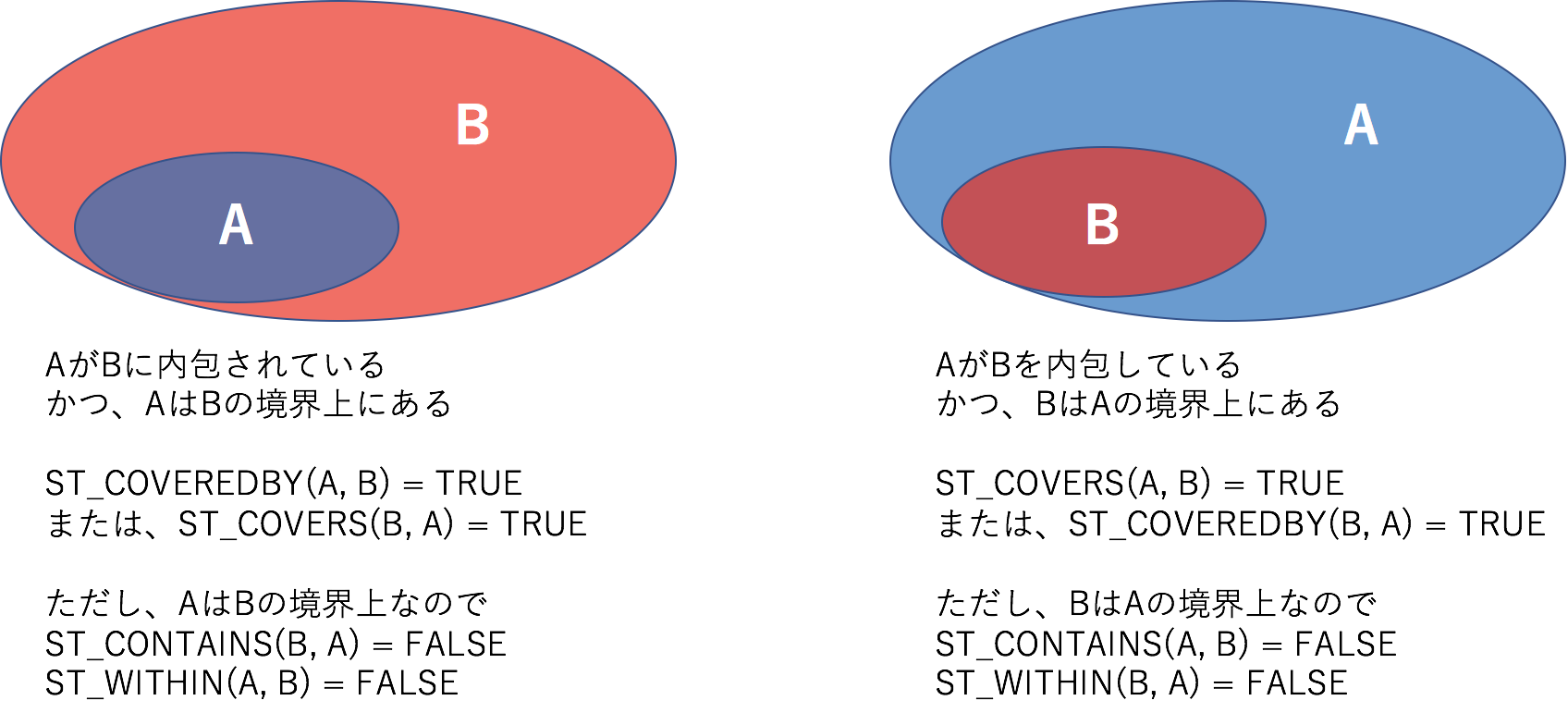
  • ST_COVEREDBY

    • ST_COVEREDBY(geography_1, geography_2)
    • ST_COVEREDBY(a, b)はAがBに内包されていればTRUEを返却します
    • AがBからはみ出していたらFALSEが返却されます
    • ST_COVERS(b, a)と同じです

  • ST_COVERS

    • ST_COVERS(geography_1, geography_2)
    • AがBを内包していたらTRUEが返却されます
    • BがAの境界上にあったら、TRUEが返却されます
    • この点がST_CONTAINSとの違いです
    • image-20181222100106956.png

  • ST_DISJOINT

    • ST_DISJOINT(geography_1, geography_2)
    • AとBの共通部分が存在しなければTRUEを返します
    • つまり完全に排他であればTRUEを返します
    • ST_DISJOINTはST_INTERSECTSの否定の論理関係にあります
    • すなわちST_DISJOINTはTRUEを返却するとき、ST_INTERSECTSはFALSEを返却します
    • image-20181222100337043.png

  • ST_DWITHIN

    • ST_DWITHIN(geography_1, geography_2, distance[, spheroid=FALSE])
    • geography_1とgeography_2の幾何形状が少なくとも一点以上、所定の距離以内に収まっていればTRUEを返却します。入っていなければFALSEを返します。
    • spheroid=FALSEが指定された場合は、距離は完全な球として計算されます
    • spheroid=TRUEが指定された場合は、WGS84の楕円曲面として距離計算が行われます。
    • image-20181222101427728.png

  • ST_EQUALS

    • ST_EQUALS(geography_1, geography_2)
    • geography_1とgeography_2が同じGEOGRAPHYを表現する場合はTRUEを返却します
    • ST_COVERS(geography_1, geography_2) = TRUE かつ ST_COVERS(geography_2, geography_1) = TRUE
    • または両方がemptyのとき

  • ST_INTERSECTS

    • ST_INTERSECTS(geography_1, geography_2)
    • geography_1とgeography_2が共通部分を持つとき、TRUEを返却します
    • ST_INTERSECTSはST_DISJOINTの否定の論理関係を持ちます
    • すなわちST_INTERSECTSがTRUEを返却するとき、ST_DISJOINTはFALSEを返却します

  • ST_INTERSECTSBOX

    • ST_INTERSECTSBOX(geography, lng1, lat1, lng2, lat2)
    • 入力となるgeographyが[lng1, lng2]と[lat1, lat2]から構成される矩形と共通部分を持つときTRUEを返却します
    • image-20181201232931199.png

  • ST_TOUCHES

    • ST_TOUCHES(geography_1, geography_2)
    • geography_1とgeography_2が接触しているときにTRUEを返却します。
    • しかし互いに共通部分に面積を持ってはいけません。
    • すなわち
    • ST_INTERSECTS(geography_1, geography_2) = TRUE
    • ST_DISJOINT(geography_1, geography_2) = TRUE
    • image-20181201234025797.png

  • ST_WITHIN

    • ST_WITHIN(geography_1, geography_2)
    • geography_1の全ての頂点がgeography_2の外に存在しない
    • かつ、geography_1の内部の頂点がgeography_2に全て内包されている
    • 場合にTRUEを返却する
    • ST_WITHIN(a, b)はST_CONTAINS(b, a)と同じ結果を返す
    • image-20181201234717795.png

  • ST_ISEMPTY

    • ST_ISEMPTY(geography_expression)
    • 入力されるGEOGRAPHYが空のときに、TRUEを返却する

  • ST_ISCOLLECTION

    • ST_ISCOLLECTION(geography_expression)
    • 入力されるGEOGRAPHYが少なくとも一つ以上の頂点を持つときにTRUEを返却する
    • 空であるGEOGRAPHYはFALSEとなる

  • ST_DIMENSION

    • ST_DIMENTION(geography_expression)
    • 入力されるGEOGRAPHYの次元数を返却する
    • 入力GEOGRAPHYが複数の幾何形状の組み合わせの場合は最大となる次元数が返却される
    • pointの次元は0
    • linestringの次元は1
    • polygonの次元は2
    • emptyとなるGEOGRAPHYは-1が返却される

  • ST_NUMPOINTS

    • ST_NUMPOINTS(geography_expression)
    • 入力されるGEOGRAPHYの頂点数を返却する
    • NOTE: ポリゴンの始めと終わりの頂点は同じ緯度経度を示すもののそれぞれ別々の頂点として計算される

  • ST_AREA

    • ST_AREA(geography_expression[, spheroid=FALSE])
    • 入力されるGEOGRAPHYの面積を$ m^2 $単位で返却する
    • pointやlineが入力された場合は0を返却する
    • collectionが入力された場合はpolygonの面積の合計を返却する
    • spheroid=FALSEが指定された場合は、距離は完全な球として計算されます
    • spheroid=TRUEが指定された場合は、WGS84の楕円曲面として距離計算が行われます。

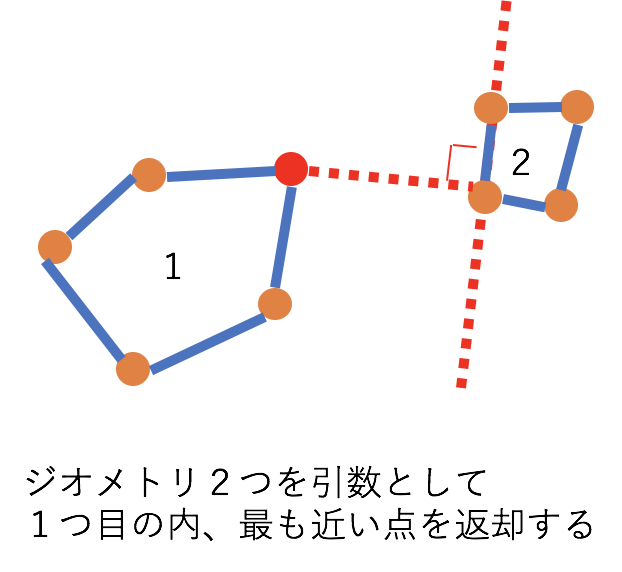
  • ST_DISTANCE

    • ST_DISTANCE(geography_1, geography_2[, spheroid=FALSE])
    • 二つのGEOGRAPHY間の最短距離を$m$単位で返却する
    • GEOGRAPHYのどちらか片方がemptyの場合は、NULLを返却する
    • spheroid=FALSEが指定された場合は、距離は完全な球として計算されます
    • spheroid=TRUEが指定された場合は、WGS84の楕円曲面として距離計算が行われます。

  • ST_LENGTH

    • ST_LENGTH(geography_expression[, spheroid=FALSE])
    • 入力されるGEOGRAPHYがlineである場合、合計の長さを$m$単位で返却する
    • 入力がpointやpolygonである場合は0を返却する
    • collectionが入力された場合はlineの長さの合計を返却する
    • spheroid=FALSEが指定された場合は、距離は完全な球として計算されます
    • spheroid=TRUEが指定された場合は、WGS84の楕円曲面として距離計算が行われます

  • ST_MAXDISTANCE

    • ST_MAXDISTANCE(geography_1, geography_2[, spheroid=FALSE])
    • 二つのジオメトリ間の距離が最大となる二点間の距離を計算する

  • ST_PERIMETER

    • ST_PERIMETER(geography_expression[, spheroid=FALSE])
    • 入力となるGEOGRAPHYの外周の長さの合計を$m$単位で返却します
    • pointおよびlineの場合は0が返却されます
    • collectionが入力される場合はpolygonの外周の合計が返却されます
    • spheroid=FALSEが指定された場合は、距離は完全な球として計算されます
    • spheroid=TRUEが指定された場合は、WGS84の楕円曲面として距離計算が行われます

  • ST_UNION_AGG

    • ST_UNION_AGG(geography)
    • 入力となった全てのGEOGRAPHYを一つの点集合としてまとめたGEOGRAPHYを返却します
    • ST_UNIONとは違い、geography collectionを入力としてUNIONを行う

ニューヨークのタクシーデータ

それでは、ここから、実際にBigQueryでSQLを使ってみましょう。今回はBigQuery上でサンプルとして使えるPublicデータであるニューヨークのタクシーデータを利用してみます。

ニューヨークでは、3種類のタクシーデータがオープンデータとして公開されています。黄色いイエローキャブと青リンゴ色のボロ・タクシーとFor-Hire Vehicleのタクシーです。今回はイエローキャブのデータについて調べてみます。

SELECT
  count(*) as pickup_num
FROM
  bigquery-public-data.new_york_taxi_trips.tlc_yellow_trips_2018
GROUP BY
  pickup_location_id

2018年は、イエローキャブが63,356,111回乗られているようです。

イエローキャブはどのエリアで特に乗られているのでしょうか？可視化してみましょう。

# standardSQL
WITH
tbl_a as (
SELECT
  zone_id,
  zone_name,
  borough,
  zone_geom
FROM
  `bigquery-public-data.new_york_taxi_trips.taxi_zone_geom`
),
tbl_b as (
SELECT
  pickup_location_id,
  count(*) as pickup_num
FROM
 `bigquery-public-data.new_york_taxi_trips.tlc_yellow_trips_2018`
GROUP BY
  pickup_location_id
)
SELECT
  tbl_a.zone_id,
  tbl_a.zone_geom,
  coalesce(tbl_b.pickup_num, 0) as total_pickup_num
FROM
  tbl_a
  left outer join tbl_b
  on tbl_a.zone_id = tbl_b.pickup_location_id

可視化結果を見てみましょう。

image-20181203073041080.png

BigQueryはGoogle Map上の可視化ツールであるGeo Vizを提供しています。これにより、SQLを実行するだけで、上記の様な位置情報の可視化が可能となります。Geo VizはGUIからどのように色付けを行うかスタイルを簡単に設定することが可能で大変便利です。

さて、ニューヨークのイエローキャブはマンハッタンに集まる傾向が強いですが、マンハッタン以外にも２箇所乗られることが多いエリアがある様です。

興味が湧いたのでグリーンキャブ（ボロ・タクシー）についても見てみましょう。コードはテーブル名をtlc_green_trips_2018を参照する様に変更したのみです。

# standardSQL
WITH
tbl_a as (
SELECT
  zone_id,
  zone_name,
  borough,
  zone_geom
FROM
  `bigquery-public-data.new_york_taxi_trips.taxi_zone_geom`
),
tbl_b as (
SELECT
  pickup_location_id,
  count(*) as pickup_num
FROM
  `bigquery-public-data.new_york_taxi_trips.tlc_green_trips_2018`
GROUP BY
  pickup_location_id
)
SELECT
  tbl_a.zone_id,
  tbl_a.zone_geom,
  coalesce(tbl_b.pickup_num, 0) as total_pickup_num
FROM
  tbl_a
  left outer join tbl_b
on tbl_a.zone_id = tbl_b.pickup_location_id

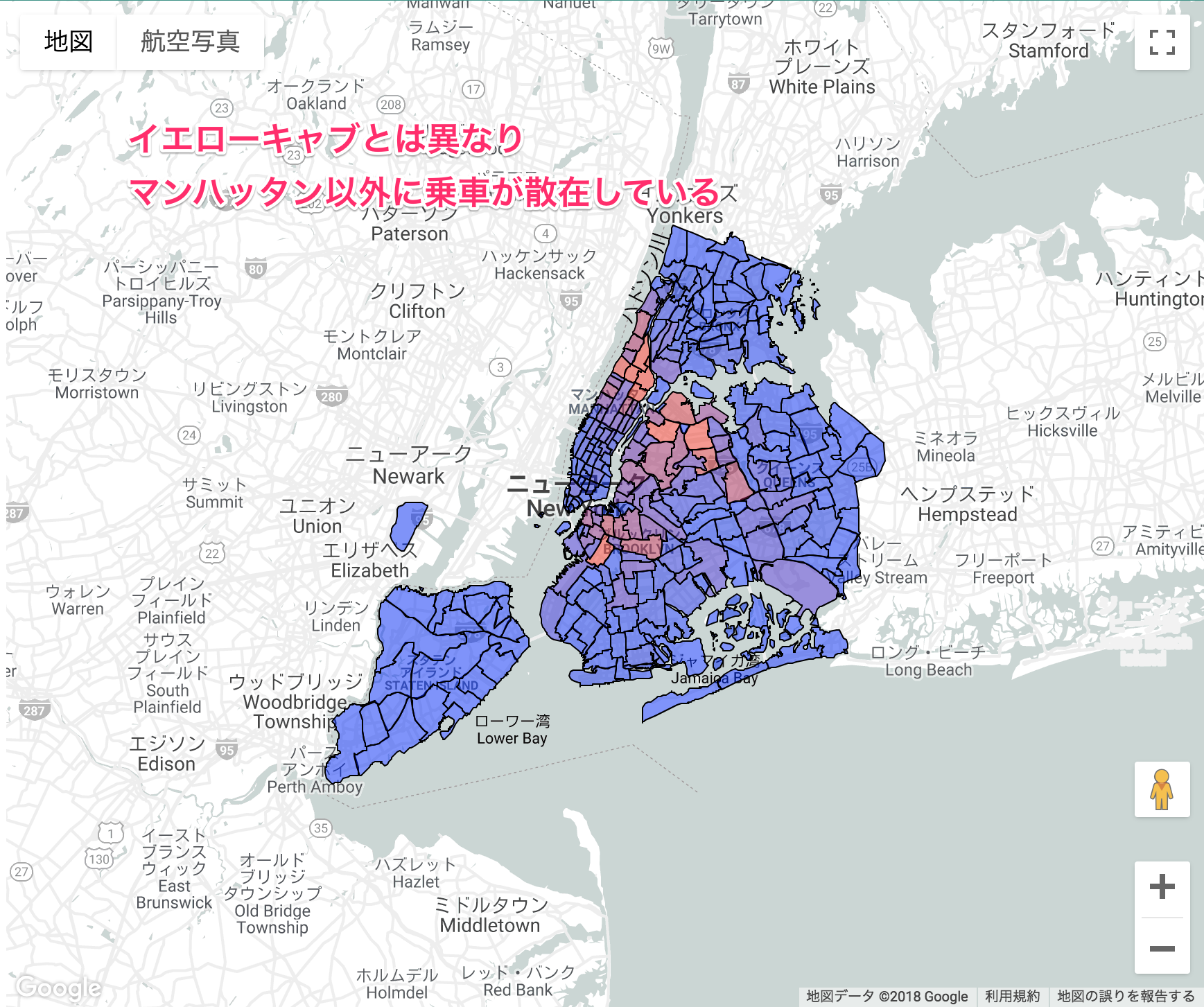
image-20181203073922508.png

イエローキャブと比べるとそもそものスケールが小さいのですが、マンハッタン以外での営業を増やすために導入されたボロタクシーであり、マンハッタン以外の領域に散在していることが確認できて面白いですね。

57
33
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
57
33