【Pycaret】California housingの回帰問題を解く

1.初めに

本記事も回帰問題に関する内容である。
PyCaretは機械学習手法の比較⇒ハイパーパラメータのチューニング
⇒モデル構築までをローコードでほぼ自動化できる便利なライブラリである。
私もよく使うため、解説する。

回帰問題の設定は、sklearnのCalifornia Housingのデータセットを使用し、
全体の20％を未知データとして設定。
全体の80％のデータの内、2割：testdata、8割:traindataとして設定。
トレーニング後、未知データのMedHouseValの予測精度をRMSEで評価することとした。

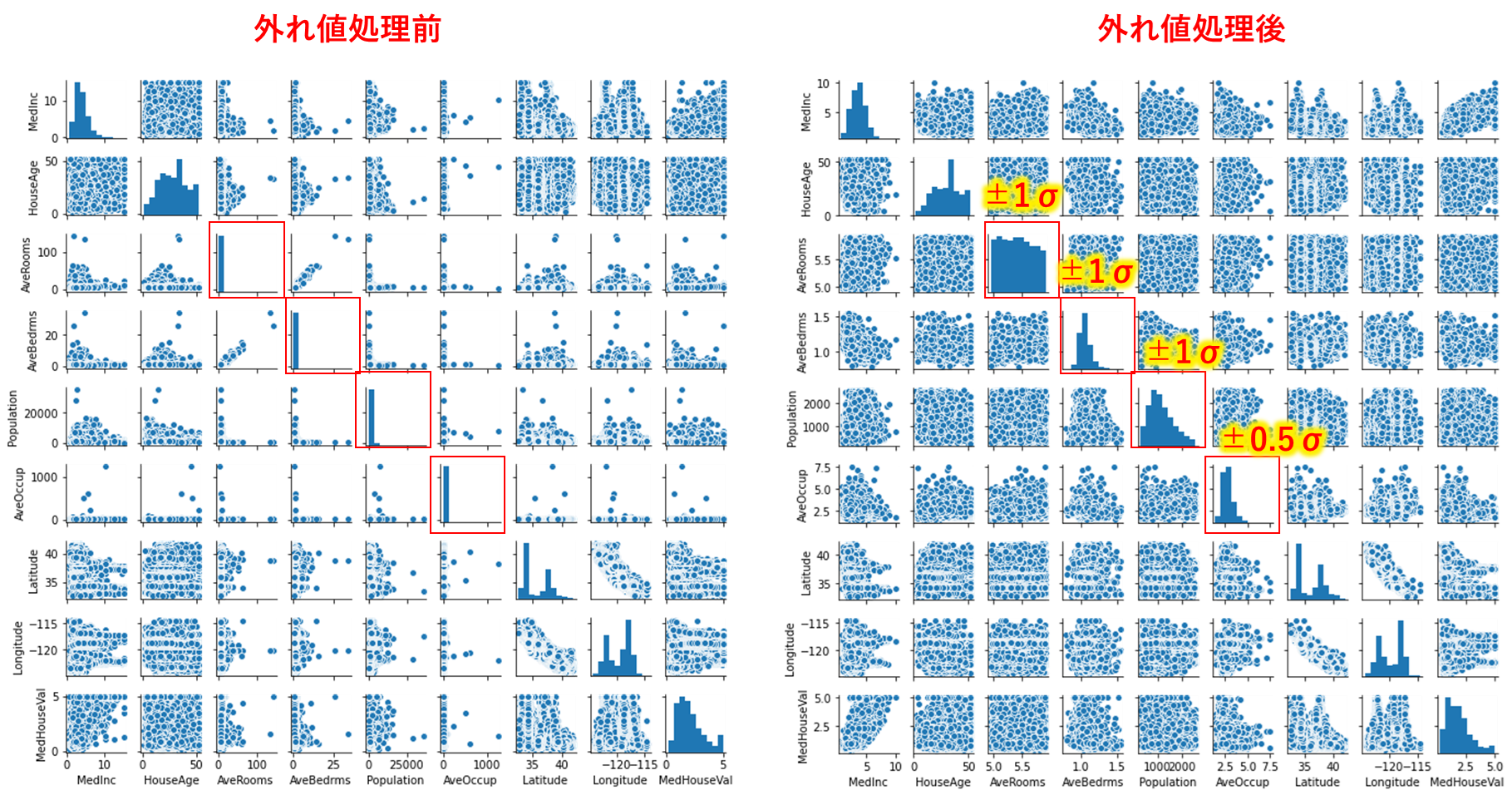
2.データの前処理

この章は前回の記事とほとんど同じなので、参照して頂きたい。
前回記事との変化点は、外れ値処理に適用した標準偏差の範囲が異なる。

# ライブラリのインポート
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_california_housing

cali_housing = fetch_california_housing(as_frame=True)
x=cali_housing.data
y=cali_housing.target

df=cali_housing.frame

###外れ値処理(多変量連関図で確認しながら標準偏差で外れ値を処理)
ar_std=df['AveRooms'].std()
ab_std=df['AveBedrms'].std()
pop_std=df['Population'].std()
ao_std=df['AveOccup'].std()

ar_mean=df['AveRooms'].mean()
ab_mean=df['AveBedrms'].mean()
pop_mean=df['Population'].mean()
ao_mean=df['AveOccup'].mean()

limit_low=ar_mean - 1*ab_std
limit_high=ar_mean + 1*ab_std

limit_low1=ab_mean - 1*ab_std
limit_high1=ab_mean + 1*ab_std

limit_low2=pop_mean - 1*pop_std
limit_high2=pop_mean + 1*pop_std

limit_low3=ao_mean - 0.5*ao_std
limit_high3=ao_mean + 0.5*ao_std

newdf=df.query('@limit_low < AveRooms < @limit_high')
newdf1=newdf.query('@limit_low1 < AveBedrms < @limit_high1')
newdf2=newdf1.query('@limit_low2 < Population < @limit_high2')
newdf3=newdf2.query('@limit_low3 < AveOccup < @limit_high3')

#正規化(Max-Min法)
def minmax_norm(df):
    return (df - df.min()) / ( df.max() - df.min())

df_minmax_norm = minmax_norm(newdf3)
#入力因子をxに代入
x=df_minmax_norm.iloc[:,:8]
#出力因子をyに代入
y=df_minmax_norm.iloc[:,8:9]

from sklearn.model_selection import train_test_split
#全体データから未知データを生成
x_know,x_unknown,y_know,y_unknown=train_test_split(x,y,test_size=0.2)
#既知データから訓練データとテストデータに分割
x_train,x_test,y_train,y_test=train_test_split(x_know,y_know,test_size=0.2)

#訓練データ(入力因子)を保存
np.savetxt("x_train_ori.csv",x_train,delimiter=',')
#学習データ(入力因子)を保存
np.savetxt("x_test_ori.csv",x_test,delimiter=',')
#未知データ(入力因子)を保存
np.savetxt("x_unknown.csv",x_unknown,delimiter=',')

#訓練データ(出力因子)を保存
np.savetxt("y_train_ori.csv",y_train,delimiter=',')
#学習データ(出力因子)を保存
np.savetxt("y_test_ori.csv",y_test,delimiter=',')
#未知データ(出力因子)を保存
np.savetxt("y_unknown.csv",y_unknown,delimiter=',')

Pycaretではラベル付きのdataframeのデータセットが必要なため下記の処理で
データセットの結合を実施する

df_train = pd.concat([x_train, y_train], axis=1) 
df_test = pd.concat([x_test, y_test], axis=1) 
df_unknown = pd.concat([x_unknown, y_unknown], axis=1) 
df_train.to_csv("./train.csv")
df_test.to_csv("./test.csv")
df_unknown.to_csv("./unknown.csv")

3.Pycaretでのモデル構築

3.1ライブラリのインポート

必要なライブラリをインポートします。

import numpy as np
import matplotlib.pyplot as plt
import plotly
import pandas as pd
import os
import seaborn as sns

from pycaret.regression import *
from sklearn import preprocessing,linear_model,svm,ensemble
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split,cross_val_score
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

3.2データのインポート

2.で前処理したtrainデータ、testデータをインポートする。

#データインポート
data_train = pd.read_csv('train.csv')
data_test = pd.read_csv('test.csv')

3.3Pycaretの起動

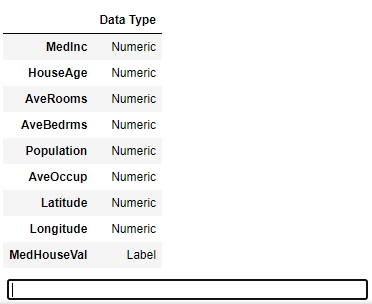
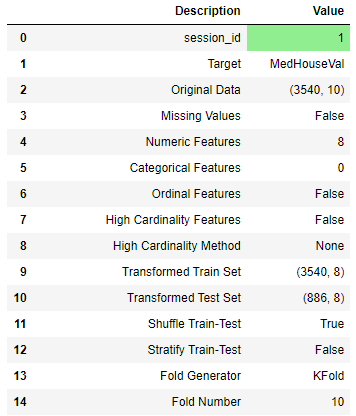
#pycaret起動
expl=setup(data_train,#訓練データを記入
           target='MedHouseVal',#目的関数のラベルを記入
           test_data=data_test,#テストデータを記入
           session_id=1,#再現性確認のための乱数ID
           normalize=False,#正規化済みのためFalseを選択
           transformation=False,
           transform_target=False,
           numeric_features=[],#すべての因子が入力因子とするため空
           ignore_features=['Unnamed0']#無視する因子を記入
          )

実行後、目的関数がLabelになっていること、入力因子がNumericになっていることを確認する。
そして、Enterキーを押します。その後、下図のように設定値一覧を確認する。

3.4モデルの比較

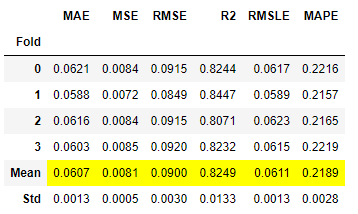
Pycaretで一括で複数の機械学習手法での精度を比較する。
foldはk分割交差検証の設定で、本記事では4分割とした。

#モデルの比較
compare_models(sort='rmse',fold=4,n_select=3)

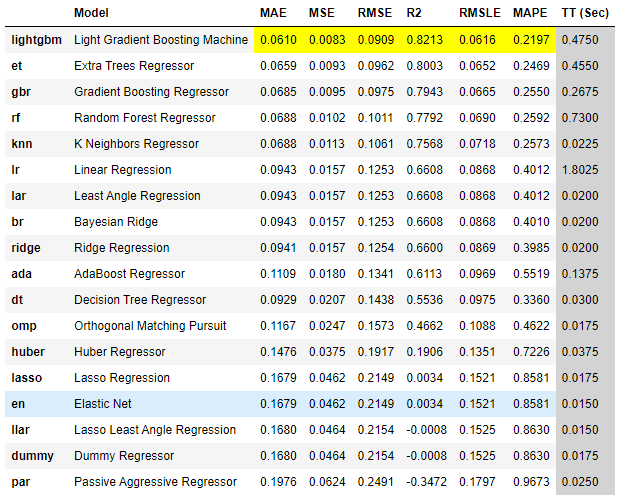
実行の結果、Light Gradient Boosting Machine(以下,LGBM)手法が最も良い結果が得られた。

3.5モデルのハイパーパラメータの最適化

続いて、LGBMのハイパーパラメータをチューニングします。
収束回数は1000回、RMSEを最小化する設定とします。

#モデルのパラメータ最適化
lgbm=create_model('lightgbm',fold=4)
tuned_lgbm=tune_model(lgbm,n_iter=1000,optimize='rmse',fold=4)

3.6Pycaretで作成したモデルの保存

チューニングを終えたモデルを保存します。

#モデルの保存
save_model(tuned_lgbm,'LighGBM_model')

4.Pycaretで保存したモデルをロードして未知データ予測する

未知データを予測します。

#未知データを読み込み
unknowndata=pd.read_csv('unknown.csv')
#saveしたモデルをload
lmodel=load_model('LightGBM_model')
#未知データを予測する
new_pred=predict_model(lmodel,data=unknowndata)
y_true=new_pred['MedHouseVal']
y_pred=new_pred['Label']

5.評価

予測した結果のRMSEを評価する。

import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
#RMSEを計算
rmse = mean_squared_error(y_true,y_pred, squared=False)
# 結果確認
plt.figure(figsize=(5,5))
plt.xlim(0,1)
plt.ylim(0, 1)
plt.plot(y_pred,y_true, 'o')
plt.title('Use LightGBM     RMSE: {:.4f}'.format(rmse))
plt.xlabel('Predict')
plt.ylabel('Actual')
plt.grid()
plt.show()

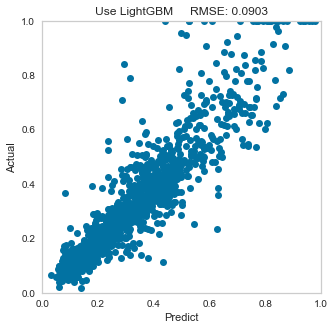
以上のように、たった数行で機械学習手法の一連の流れを実行できてしまいます。
また、前回の記事DNN回帰予測よりも高精度で予測できていることが確認できます。

6.最後に

Pycaretを上手に活用できれば、効率的に問題解決を図れるかと考えます。
最後までお読みいただきありがとうございました。

付録

Pycaretはモデルをブレンドすることができます。
LGBMのハイパーパラメータのチューニングは3.5節で済んでいるため、
Gradient Boosting Regressor(以下,GBR)のパラメータチューニングを実施し、
LGBMとGBRのブレンドを実施し、実力を把握してみようと思います。

#モデルのパラメータ最適化
gbr=create_model('gbr',fold=4)
tuned_gbr=tune_model(gbr,n_iter=1000,optimize='rmse',fold=4)
#モデルのブレンド methodオプションではhard(多数決)、soft(確率)があるようです。
ble_model=blend_models(estimator_list = [tuned_lgbm,tuned_gbr])
#
new_pred2=predict_model(ble_model,data=unknowndata)

実行後、LGBM+GBRのブレンドモデルはさらに精度が向上している結果になっています。


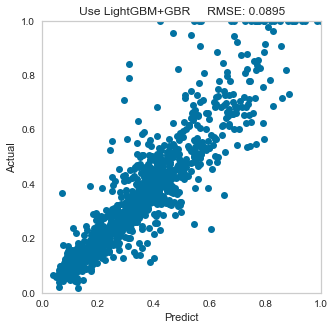
こちらも使い方次第では有効な手段だと考えます。
以上です。