ユニークビジョンプログラミングコンテスト2022(AtCoder Beginner Contest 248) A~D問題の解説記事です。
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
ユニークビジョン株式会社様について
ユニークビジョン株式会社様はSNSマーケティングツール「Belugaシリーズ」を開発しています。
興味のある方は求人情報を御覧ください。(採用は緑以上が目安のようです)
A - Lacked Number
0~9までの数字がSに含まれるか確認していきます。
ある文字がSに含まれるかは
if 文字 in S:
と書けば判定できます。逆に含まれないという場合はnotをつけて
if 文字 not in S:
と書きます。
例えば「1」が含まれるないかは
if "1" not in S:
と書いて判定します。「1」は数字でなく文字列なので「""」(ダブルクオーテーション)が必要なことに注意してください。
0~9までの数字を順番に確認しましょう。0~9までifを並べて答えを確認します。(提出1)
なお、0~9まで確認するところではforループを使うこともできます。(提出2)
for i in range(最後の数+1):
と書くことでi=0~9を代入して処理できます。
iを文字列にしなければならないので、ダブルクオーテーションの代わりにstrを使います。str(x)とするとxを文字列にしてくれます。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出1】
# 入力の受け取り
S=input()
# 「0」がSに含まれないならば
if "0" not in S:
# 「0」を出力
print(0)
elif "1" not in S:
print(1)
elif "2" not in S:
print(2)
elif "3" not in S:
print(3)
elif "4" not in S:
print(4)
elif "5" not in S:
print(5)
elif "6" not in S:
print(6)
elif "7" not in S:
print(7)
elif "8" not in S:
print(8)
elif "9" not in S:
print(9)
【提出2】
# 入力の受け取り
S=input()
# i=0~9
for i in range(10):
# i(を文字列にしたもの)がSに含まれないならば
if str(i) not in S:
# iを出力
print(i)
B - Slimes
B匹以上になるまで何回叫ぶか、実際にシミュレーションして確認します。
i回叫ぶとスライムの数はA*(K^i)匹になります。i=0,1,2,...とB匹以上になるまで計算していきます。
制約はB≤10^9なので最大でも30回叫べば必ずB以上になります。が、iの範囲をぎりぎりにするとなにか勘違いがあった時WAになってしまうので、てきとうに大きな数までを範囲にしておきましょう。
ところでB≤A*K^xという不等式から答えは「logK(B/A)の切り上げ」と計算した人がいるかもしれません。
数学的に間違いではないのですが、これは実装するとWAになります。log、B/Aの計算において少数が発生するためです。
コンピュータは無限小数を丸めて計算するため、誤差が出てしまいます。
【提出】
# 入力の受け取り
A,B,K=map(int,input().split())
# i=0,1,2,...
for i in range(10000000):
# スライムの数がB以上になったら
if B<=A*(K**i):
# 「i」を出力
print(i)
# 途中終了
exit()
C - Dice Sum
DPで解きます。
DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。
DPの解説動画を作りましたので、本問が難しいと感じた方は是非御覧ください。
https://www.youtube.com/watch?v=gVJ16ThsJYs
具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する
例として以下の入力を考えましょう。
N:4
M:4
K:7
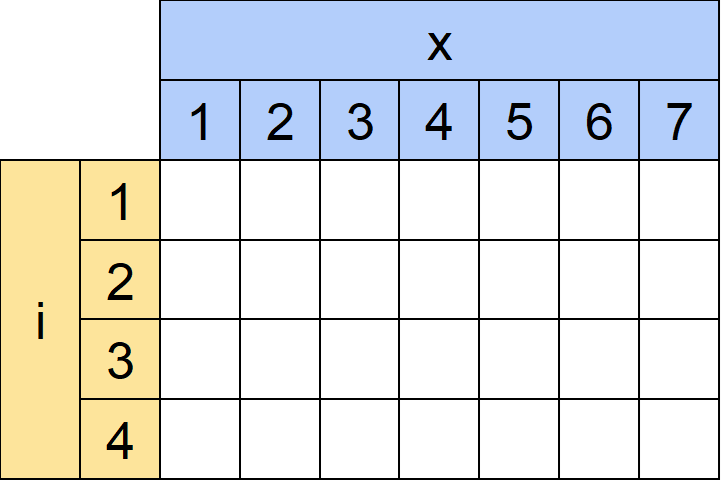
(1)表を作る
作る表は「長さがiで、合計がxであるような数列の個数」とします。表の名前はdpとします。
例えばdp[3][4]なら「長さが3で、合計が4であるような数列の個数」です。
(2)すぐにわかるところを埋める
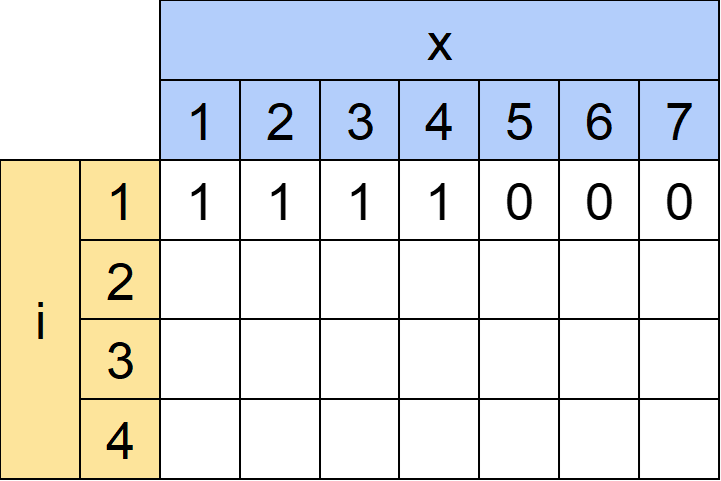
すぐにわかるのは1行目です。1行目は「長さが1で、合計がxであるような数列の個数」を表します。
長さが1の数列というのは要するに(1),(2),(3),...のことです。
例えばdp[1][1]というのは(1)の1個しかありません。dp[1][2],dp[1][3]も同様に(2),(3)の1個しかありません。
さらにM=4であるために(5),(6),(7)は作ることができません。よってdp[1][5],dp[1][6],dp[1][7]は0になります。
一般に考えると以下のようになります。
・(x≤M)dp[1][x]=1
・(M<x)dp[1][x]=0
(3)表の小さい方から答えにたどり着くまで埋める
2行目を考えましょう。2行目は「長さが2で、合計がxであるような数列の個数」を表します。
例えばdp[2][3]なら「長さが2で、合計が3であるような数列の個数」です。これは(1,2),(2,1)の2個があります。
すでに1行目、長さが1で合計がxの数列の個数はわかっています。長さが1の数列に数字をくっつけることで長さが2の数列を作れます。
例えばdp[1][1]で作った数列、(1)に「1」をくっつけることで(1,1)が作れ、長さが2、合計が2の数列が作れます。これ以外に長さが2で合計が2(dp[2][2])を作ることはできません。
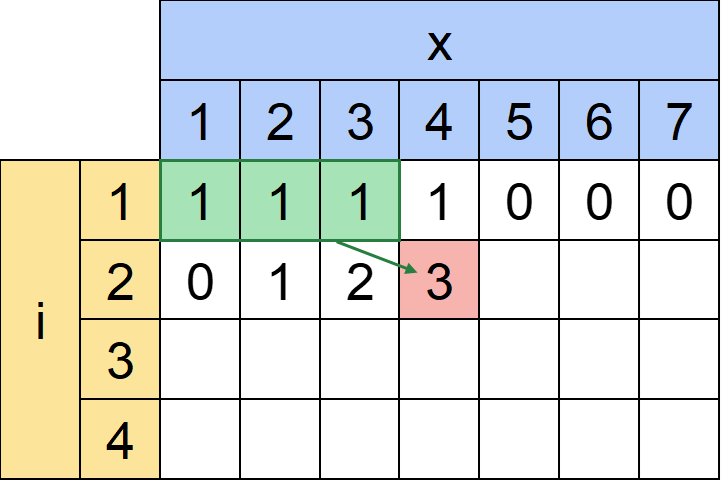
他にdp[2][4]の作り方を考えると、
dp[1][1]で作った(1)に「3」をくっつけて(1,3)
dp[1][2]で作った(2)に「2」をくっつけて(2,2)
dp[1][3]で作った(3)に「1」をくっつけて(3,1)
と3個作れます。
これは表でいうとひとつ上の行の3以下の列を足しているのと同じです。
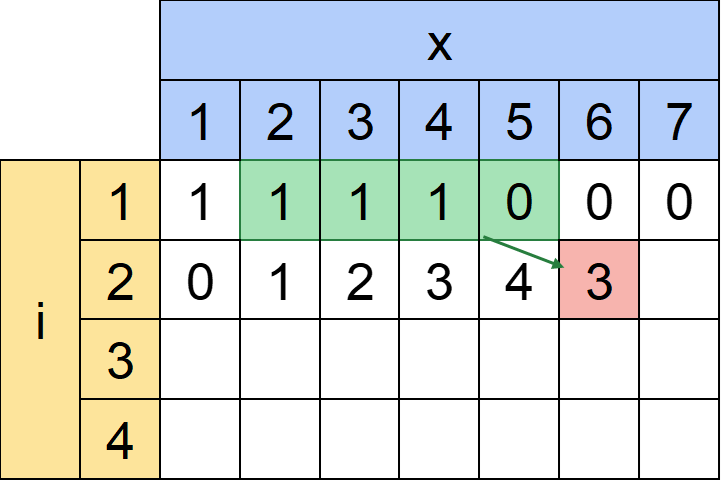
同様にdp[2][6]を考えてみましょう。
dp[1][1]で作った(1)に「5」をくっつけて(1,5)
dp[1][2]で作った(2)に「4」をくっつけて(2,4)
dp[1][3]で作った(3)に「3」をくっつけて(3,3)
dp[1][4]で作った(4)に「2」をくっつけて(4,2)
と、4個作れそうなところですがM=4なので『dp[1][1]で作った(1)に「5」をくっつけて(1,5)』はできません。
これは表でいうとひとつ上の行を4(=M)列分足しているのと同じです。
これを一般化すると以下のようになります。
・(2≤i)dp[i][x]=(dp[i-1][x-M]~dp[i-1][x-1]の和)
(4)答えを出力する
一般化した式で表を埋めると以下のようになります。
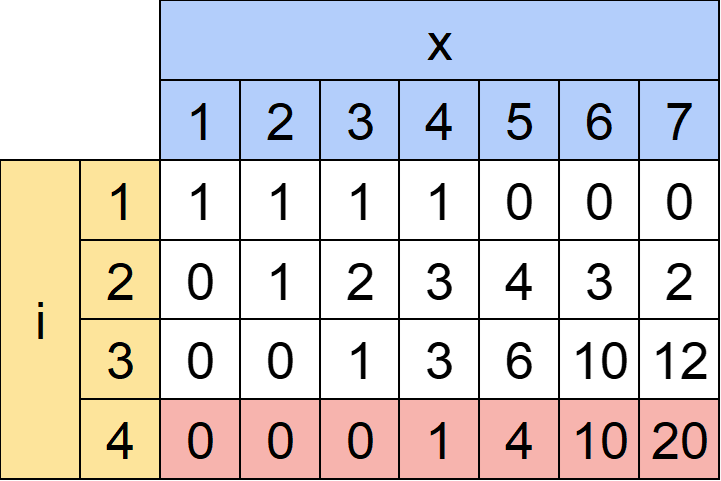
最後の行(i=4)は「長さが4で、合計がxであるような数列の個数」を表します。
よってdp[4][1]~dp[4][7]の総和が答えになります。
0+0+0+1+4+10+20=35
答えは「35」通りです。
998244353で割った余りは答えの出力直前ではなく、計算の都度取るようにしてください。計算の途中で桁数が大きくなりすぎるとTLEする場合があります。
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N,M,K=map(int,input().split())
# 余りの定義
mod=998244353
# (1)表を作る
dp=[[0]*(K+1) for i in range(N+1)]
# (2)すぐにわかるところを埋める
# ・(x≤M)dp[1][x]=1
# ・(M<x)dp[1][x]=0
for x in range(1,M+1):
dp[1][x]=1
# (3)表の小さい方から答えにたどり着くまで埋める
# i=2~N
for i in range(2,N+1):
# x=1~K
for x in range(1,K+1):
# a=(x-M)~(x-1)
for a in range(x-M,x):
# aが1未満のとき
if a<1:
# 次のaへ
continue
# ・(2≤i)dp[i][x]=(dp[i-1][x-M]~dp[i-1][x-1]の和)
dp[i][x]+=dp[i-1][a]
# 余りを取る
dp[i][x]%=mod
# (4)答えを出力する
# 答え
ans=0
# x=1~K
for x in range(1,K+1):
# dp[N][1]~dp[N][K]の和
ans+=dp[N][x]
# 余りを取る
ans%=mod
# 答えを出力
print(ans)
D - Range Count Query
クエリが与えられる度区間にあるXの数を数えていると当然TLEします。
例として以下のような入力を考えます。
N:8
A:1 2 3 1 1 2 1 4
1,2,3,...について、Aのインデックス番号の何番目に来るかを記録しましょう。
例えば「1」については以下のようになります。

黄色部分は単なる通し番号だと思ってください。
1番目の「1」はA1=1
2番目の「1」はA4=4
3番目の「1」はA5=5
4番目の「1」はA7=7
というように確認します。
実装をやりやすくするため、左端に「0」、右端に「∞」を付け足します。
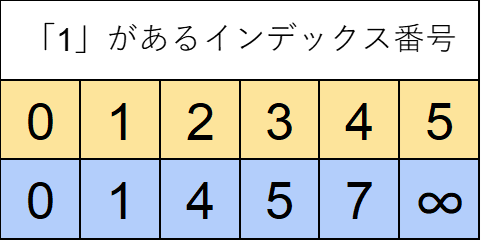
クエリ「3 7 1」が来た時、どうすれば計算できるか考えましょう。
L:3
R:7
X:1
まず右端から考えます。R=7は上表青い部分の4番目にあります。
次に左端です。L=3ですが3未満となるインデックスは上表青い部分の1番目にあります。
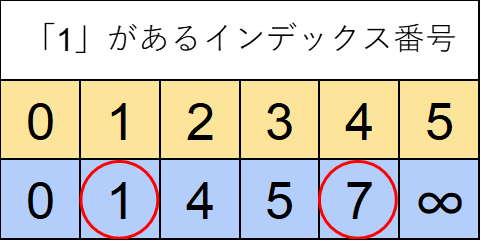
ここで黄色い部分を見ましょう。
右端=7は4番目にあります。これはA1~A7の中に「1」が4個あることを意味しています。
左端=3未満となる数は1番目にあります。これはA1~A2(3未満=2)の中に「1」が1個あることを意味しています。
ということは4個-1個=3個の「1」がA3~A7の中にあるということです。
これを一般に考えるとAL~ARの間にあるXの数は
(R以上で最小のXが何番目にあるか)-((L-1)以上で最小のXが何番目にあるか)
と計算できます・
「○○以上/以下で最小/最大」と言えば二分探索です。
以下の手順で(k以上で最小のXが何番目にあるか)を確認します。
左端:0
右端:インデックスの右端
中央=(左端+右端)//2として
・(中央)番目の数がk以下
→左端=中央と更新
・(中央)番目の数がkより大きい
→右端=中央と更新
これを(左端)-(右端)=1となるまで続けます。
結果得られた(左端)が(k以上で最小のXが何番目にあるか)を示しています。
二分探索が難しいと感じた方はABC231 C等簡単な問題で練習してみることをおすすめします。
問題:https://atcoder.jp/contests/abc231/tasks/abc231_c
解説:https://qiita.com/sano192/items/2b2656202b767109387e#c---counting-2
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))
# 1,2,3,...が何番目にあるかの記録 左端には「0」を入れておく
A_indx=[[0] for i in range(10**6)]
# i=0~(N-1)
for i in range(N):
# インデックス番号を記録
# 1インデックスなので「i+1」を記録することに注意
A_indx[A[i]].append(i+1)
# i=0~(N-1)
for i in range(10**6):
# 右端に∞=10^6を追加
A_indx[i].append(10**6)
# xについて、k以上で最小の数が何番目にあるかの確認
def Nibutan(x,k):
# 左端
l=0
# 右端
# 長さ-1
r=len(A_indx[x])-1
# 1<(右端)-(左端)の間
while 1<r-l:
# 中央=(左端+右端)//2
c=(l+r)//2
# ・(中央)番目の数がk以下
if A_indx[x][c]<=k:
# 左端=中央と更新
l=c
# ・(中央)番目の数がkより大きい
else:
# 右端=中央と更新
r=c
# (左端)を返す
return l
# 入力の受け取り
Q=int(input())
# Q回
for i in range(Q):
# 入力の受け取り
L,R,X=map(int,input().split())
# (L-1)以上で最小のXが何番目にあるか
indx_l=Nibutan(X, L-1)
# R以上で最小のXが何番目にあるか
indx_r=Nibutan(X, R)
# 答えを出力
print(indx_r-indx_l)
【広告】
『AtCoder 凡人が『緑』になるための精選50問詳細解説』
AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段:100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/
【booth(pdf)】
https://sano192.booth.pm/items/3179185
1~24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf
『AtCoder ABC201~225 ARC119~128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』
ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV
【booth(pdf)】
https://booth.pm/ja/items/3698647
ARC119~128の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/
【booth(pdf)】
https://sano192.booth.pm/items/3698668
『AtCoder ABC226~250 ARC129~139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』
ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS
【booth(pdf)】
https://sano192.booth.pm/items/4025713
ARC129~139の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF
【booth(pdf)】
https://sano192.booth.pm/items/4025737
『Excelでリバーシを作ろう!! マクロ、VBAを1から学ぶ』
Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です!
マクロ、VBAが全くわからない人でも大丈夫! 丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます!
値段:300円(Kindle Unlimited対象)
サンプルとして「準備」~「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb
【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW
【booth(pdf】
https://sano192.booth.pm/items/3785312