ABC254 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC254(AtCoder Beginner Contest 254)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

A - Last Two Digits　Dif:7

Nを文字列として受け取りましょう。
そうすればNの左端を0文字目、真ん中を1文字目、右端を2文字目として答えは
(Nの1文字目)+(Nの2文字目)
となります。
Nの1文字目はN[1],2文字目はN[2]と表します。
文字を連結するときは単純に「+」でくっつければOKです。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
N=input()

# Nの1文字目と2文字目を連結
ans=N[1]+N[2]

# 答えの出力
print(ans)

B - Practical Computing　Dif:45

a(i,j)を二次元配列を使い、a[i][j]と表します。
そうするとi=0,1,2,...について
・j=0　または　j=i　→　a[i][j]=1
・上記以外　→　a[i][j]=a[i-1][j-1]+a[i-1][j]
と問題文の条件通りに計算ができます。
Aiの長さ(a[i]の要素数)を(i+1)にするような二次元配列を作ることもできるのですが、面倒なのでN*Nの二次元配列を作ってしまえば良いです。
二次元配列は以下のように書いて作ります。
変数名=[[初期値]*列数 for i in range(行数)]

配列をN*Nにしたとしても答えを出力するときに余分な部分は出力しないようにすれば問題ありません。
a[i][:i+1]とすればa[i]の0~i番目のみを出力します。
更にリストの出力時、print(*(リスト名))と書くことで[]を外して出力ができます。

【提出】

# 入力の受け取り
N=int(input())

# 二次元配列を作る
a=[[0]*N for i in range(N)]

# i=0~(N-1)
for i in range(N):
    # j=0~i
    for j in range(i+1):

        # j=0 または j=iの場合
        if j==0 or j==i:
            a[i][j]=1
        
        # それ以外
        else:
            a[i][j]=a[i-1][j-1]+a[i-1][j]

# i=0~(N-1)
for i in range(N):
    # a[i]の0~i番目までを出力
    print(*a[i][:i+1])

C - K Swap　Dif:536

例として以下の入力を考えます。
N K：9 3
a：4 2 6 9 3 10 1 5 11

実装に合わせてa1=a[0],a2=a[1],...と0インデックスで説明します。

K=3であるということは以下の要素について並び替えができるということです。
・a[0]とa[3]とa[6]
・a[1]とa[4]とa[7]
・a[2]とa[5]とa[8]
これらは適当な回数の入れ替えを行うことで自由な位置に移動させることができます。
以下図の同じ色のものが入れ替え可能ということです。

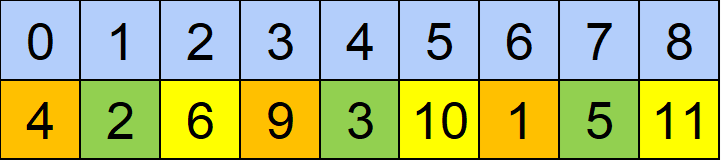
例えばa[0]=1,a[3]=4,a[6]=9というように値を変更できます。逆にこれら以外の値を入れ替える事はできません。
この下にソート後のaを書いてみましょう。

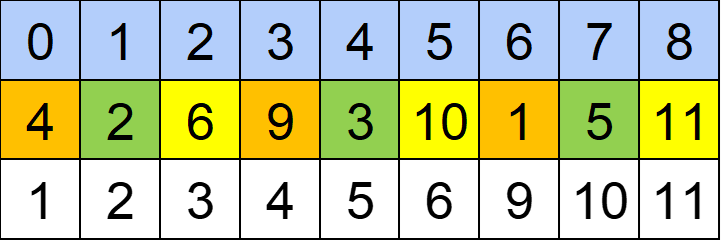
てきとうな回数入れ替えを行ってソート後のaと一致させることができれば「Yes」です。
ソート後のほうにも色をつけてみます。

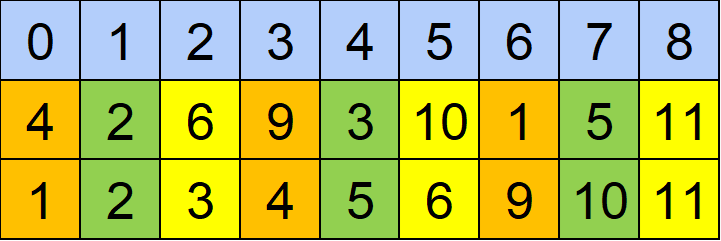
・a[0]とa[3]とa[6]について
オレンジの部分にあたります。
ソート前のaは「4」「9」「1」があります。
ソート後のaは「1」「4」「9」があります。
両方同じ数字を同じ数だけ持っていますから、てきとうに入れ替えることでソート後のaと一致させることができます。

・a[1]とa[4]とa[7]
緑の部分にあたります。
ソート前のaは「2」「3」「5」があります。
ソート後のaは「2」「5」「10」があります。
持っている数字が違いますから、どう頑張ってもソート後のaと一致させることができません。
よってこの時点で答えは「No」とわかります。

一般には
ソート前とソート後のaについてi番目,(i+K)番目,(i+2K)番目,...が同じ数字を同じ数だけ持っているか？
を確認すれば判定ができるということになります。

持っている数の管理にはdefaultdictを使うと楽でしょう。
連想配列(defaultdict)を使ったことがない人は以下を参照してください。

defaultdict(連想配列)について
辞書または連想配列と言います。
キー：値
というような対応付を行えるデータ構造です。
連想配列はdict()と書くことでも使えますが、デフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import：from collections import defaultdict
作成(デフォルト0)：変数名=defaultdict(int)
キー、値の登録：変数名[キー]=値
値の取り出し：変数名[キー]
【使用例】

# インポート
from collections import defaultdict

# 作成(デフォルト0)：変数名=defaultdict(int)
dictionary=defaultdict(int)

# キー、値の登録：変数名[キー]=値
dictionary[5]=1

# 値の取り出し：変数名[キー]
x=dictionary[5]

詳しく知りたい人は以下を参照してください。

連想配列でまずソート前のaについてa[i],a[i+K],a[i+2K],...の持っている数を記録します。
次にソート後のa(=aSorted)についてaSorted[i],aSorted[i+K],aSorted[i+2K],...で出現する数をマイナスしていきます。もし数が0を下回ったらソート前のaとソート後のaで持っている数字が違うということになります。

【提出】

# 入力の受け取り
N,K=map(int,input().split())
a=list(map(int,input().split()))

# ソート後のA
aSorted=sorted(a)

# defaultdictをインポート
from collections import defaultdict

# a[i],a[i+K],a[i+2K],...に出てくる数字をカウントする連想配列
Count=defaultdict(int)

# i=0~(K-1)
for i in range(K):

    x=0
    # インデックスの範囲内である限り
    while i+K*x<N:
        # a[i+K*x]の個数をカウント
        Count[a[i+K*x]]+=1
        # 次のxへ
        x+=1
  
    x=0
    # インデックスの範囲内である限り
    while i+K*x<N:
        # ソート後のaについてaSorted[i+K*x]の個数をマイナス
        Count[aSorted[i+K*x]]-=1
        # もし個数がマイナスになったら
        if Count[aSorted[i+K*x]]<0:
            # ソート前とソート後で個数が違う
            # ⇔「No」を出力
            print("No")
            # 終了
            exit()
        
        # 次のxへ
        x+=1

# 「Yes」を出力
print("Yes")

D - Together Square　Dif:1191

i*jが平方数であるということはi*jを素因数分解したとき常に偶数個ずつの素因数となるということです。
例えば36=2*2*3*3となりますがこれは2が2個、3が2個で偶数個ずつになっていますから平方数です。
もう一つ重要なことは平方数に平方数を掛けたものも平方数となるということです。

よって次の手順で解くことができます。
i=1,2,3,...について
(1)iを素因数分解し、奇数個ある素因数を確認する。それらの素因数を全て掛け算して=jとする
(2)j*(平方数)≤Nとなるような最大の(平方数)を探す
(3)見つかった最大の(平方数)がx番目であればiに対してjがx通りあることがわかるので答えにカウントする

例を見ましょう。N=100とします。
まず平方数のリストを作っておきます。1^2,2^2,3^2,...,N^2まで用意すればよいです。これをSとします。
S=[1,4,9,16,25,...,10000]

・i=1の場合
(1)iを素因数分解し、奇数個ある素因数を確認する。それらの素因数を全て掛け算して=jとする
i=1を素因数分解すると1です。このときj=1となります。

(2)j*(平方数)≤Nとなるような最大の(平方数)を探す
1*(100)≤Nで(100)が最大の(平方数)です。

(3)見つかった最大の(平方数)がx番目であればiに対してjがx通りあることがわかるので答えにカウントする
100=10^2であり、10番目の平方数ですから、i=1に対してjは10通りが考えられます。
((i,j)=(1,1),(1,4),(1,9),...,(1,100)まで10通りです)
答えにプラス10して10通りになります。

・i=2の場合
(1)iを素因数分解し、奇数個ある素因数を確認する。それらの素因数を全て掛け算して=jとする
i=2を素因数分解すると2です。このとき2は1個しかなく、奇数個なのでj=2となります。

(2)j*(平方数)≤Nとなるような最大の(平方数)を探す
2*(49)≤Nで(49)が最大の(平方数)です。

(3)見つかった最大の(平方数)がx番目であればiに対してjがx通りあることがわかるので答えにカウントする
49=7^2であり、7番目の平方数ですから、i=2に対してjは7通りが考えられます。
((i,j)=(2,2*1),(2,2*4),(2,2*9),...,(2,2*49)まで7通りです)
答えにプラス7して17通りになります。

i=6まで飛ばします・・・

・i=6の場合
(1)iを素因数分解し、奇数個ある素因数を確認する。それらの素因数を全て掛け算して=jとする
i=6を素因数分解すると2*3です。このとき2,3は1個で奇数個なのでj=2*3=6となります。
これはつまりjの側に最低でも2が1個,3が1個なければi*jを平方数にできないという意味です。

(2)j*(平方数)≤Nとなるような最大の(平方数)を探す
6*(16)≤Nで(16)が最大の(平方数)です。

(3)見つかった最大の(平方数)がx番目であればiに対してjがx通りあることがわかるので答えにカウントする
16=4^2であり、4番目の平方数ですから、i=6に対してjは4通りが考えられます。
((i,j)=(6,6*1),(6,6*4),(6,6*9),(6,6*16)の4通りです)

これを繰り返すことによって答えを出すことができます。
(2)j*(平方数)≤Nとなるような最大の(平方数)を探す　についてはSに対して二分探索を使うことで高速に見つけることができます。

pythonでは間に合わないのでpypyで提出します。

素因数分解のやり方
素因数分解はi=2,3,4,...でひたすら試し割りを行い、割り切れたらN=N//iと置き換えを行います。これを√N<iとなるまでひたすら続けます。
このやり方は計算量がO(√N)となります。
「例」
N=1260
i=2≤√1260なので試し割りを開始
i=2：1260//2＝630(素因数に2を追加)
i=2≤√630なので試し割りを続ける
i=2：630//2＝315(素因数に2を追加)
i=2≤√315なので試し割りを続ける
i=2：315は2で割れない→次のi=3へ
i=3≤√315なので試し割りを続ける
i=3：315//3＝105(素因数に3を追加)
i=3≤√105なので試し割りを続ける
i=3：105//3＝35(素因数に3を追加)
i=3≤√35なので試し割りを続ける
i=3：35は3で割れない→次のi=4へ
i=4≤√35なので試し割りを続ける
i=4：35は4で割れない→次のi=5へ
i=5≤√35なので試し割りを続ける
i=5：35//5＝7(素因数に5を追加)
√7=2.64...<i=5となったので、試し割りが終わりです。
最後に残った7を素因数として追加します。結果として1260=2*2*3*3*5*7が得られます。

実装ではPrimeFactorizeという関数を作って上記操作を行っています。
自分で実装できるようになるのが一番ですが、慣れないうちは丸々コピペで使ってもよいでしょう。

【二分探索を実装したことがない場合】
この問題は二分探索問題としては難易度が高いため、他の問題で練習してから解くことをおすすめします。
以下が比較的簡単な二分探索問題です。
ABC146 C：https://atcoder.jp/contests/abc146/tasks/abc146_c
ABC231 C：https://atcoder.jp/contests/abc231/tasks/abc231_c

ABC231 Cは以下で解説をしています。
https://qiita.com/sano192/items/2b2656202b767109387e#c---counting-2

ABC146 Cについては拙著『AtCoder　凡人が『緑』になるための精選50問詳細解説』で解き方、二分探索のコツ、実装方法まで詳細に解説しています。
詳細は【広告】をご確認ください。

【提出】

# pypyで提出

# 素因数分解
# 引数：x　→　返り値：xの素因数リスト
# x=1の場合は空のリストを返す
def PrimeFactorize(x):
    # もしx=1ならば
    if x==1:
        # 空のリストを返す
        return []
    # 素因数を格納するリスト
    PrimeList=[]
    # i=2,3,4,...で試し割り
    i=2
    # i≤√xすなわちi**2≤xの範囲で試し割り
    while i**2<=x:
        # もしiで割り切れたら
        if x%i==0:
            # iを素因数に追加
            PrimeList.append(i)
            # xをiで割る
            x//=i
        # iで割り切れなかったら
        else:
            # 次のiへ
            i+=1
    # 試し割りが終わった時xが1でなければ
    if x!=1:
        # 素因数にxを追加
        PrimeList.append(x)
    # 素因数のリストを返す
    return PrimeList

# 入力の受け取り
N=int(input())

# N=1の場合は例外ケースとして処理
if N==1:
    print(1)
    exit()
    
# 平方数のリスト
S=[]

# i=0~Nまで
for i in range(N+1):
    # 平方数を格納
    S.append(i**2)

# 二分探索
def Nibutan(j):
    # 左端
    l=0
    # 右端
    r=N

    # 1<(右端)-(左端)　の間
    while 1<r-l:
        # 中央
        c=(l+r)//2

        # S[中央]*jがN以下の場合
        if S[c]*j<=N:
            # 左端=中央と更新
            l=c
        # そうでない場合
        else:
            # 右端=中央と更新
            r=c
    
    # 左端を返す
    return l

# 答え
ans=0

# i=1~N
for i in range(1,N+1):
    
    # 初期値の割当
    j=1

    # iの素因数分解結果
    P=PrimeFactorize(i)

    # x：iの素因数それぞれについて
    for x in set(P):
        # xが素因数リストに奇数個含まれていれば
        if P.count(x)%2==1:
            # jに掛ける
            j*=x
        
    # j*(平方数)≤Nとなる最大の(平方数)が何番目かを確認し、答えにカウント
    ans+=Nibutan(j)

# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312