ABC266 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC266(AtCoder Beginner Contest 266)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

A - Middle Letter　Dif:9

pythonではSのX文字目をS[X]と書きます。
ただし先頭は0文字目、すなわちS[0]、次がS[1]、...というようになります。
例えばS="atcoder"であればS[0]="a",S[1]="t",...となります。

中央の文字は文字数の半分のところにある文字です。
例えばS="atcoder"の時Sは7文字で、真ん中の"o"は3文字目、つまりS[3]となります。
つまり(文字数を2で割った商)文字目を出力すればいいです。

Sの文字数はlen(S)として確認します。lenはlengthの意味です。
これを2で割った商を確認します。「//」を使うと割り算の商が確認できます。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
S=input()

# (Sの文字数)を2で割った商
X=len(S)//2

# SのX文字目を出力
print(S[X])

B - Modulo Number　Dif:95

998244353の倍数と言われてもちょっと分かりづらいので、11の倍数だったらどうなるか考えましょう。
N=12の場合
12-1=11だからx=1
N=25の場合
25-3=22だからx=3
N=43の場合
43-10=33だからx=10
それぞれNを11で割った余りになっているのがわかるでしょうか。
同様にN-xを998244353の倍数にするためにはNを998244353で割った余りをxとすればOKです。
余りは「%」で確認できます。

Nが0より小さい場合でも「%」で余りをとればOKです。
(pythonであればこれでOKですが、C++の「%」は仕様が違うため、少し工夫が必要になります)

【提出】

# 入力の受け取り
N=int(input())

# 998244353で割った余りを出力
print(N%998244353)

C - Convex Quadrilateral　Dif:516

「Yes」になるパターンと「No」になるパターンをいくつか紙に描いてみましょう。

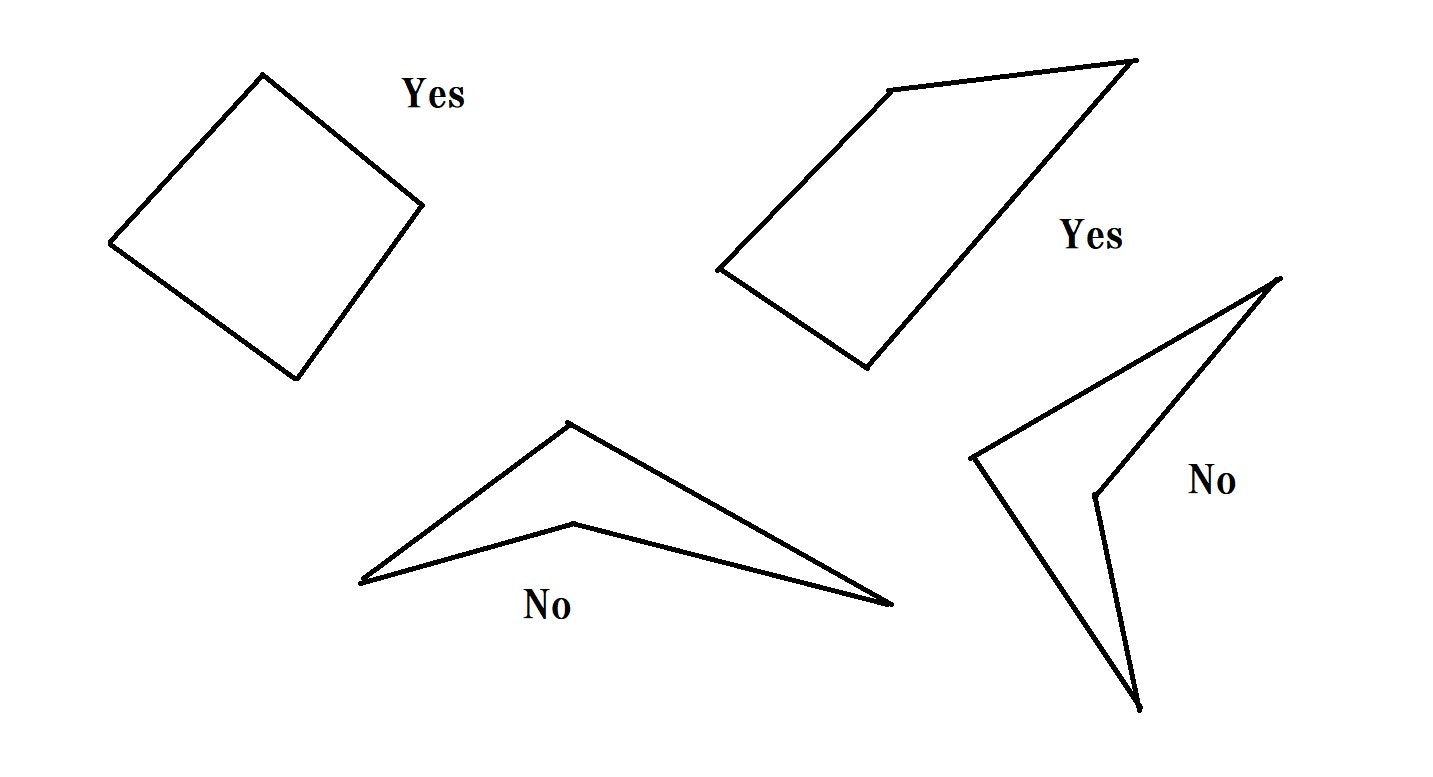
四角形の3点で三角形を作った場合、4つ目の点が三角形の外側にあれば「Yes」、内側にあれば「No」となることがわかります。
具体的には以下の条件を確認します。
・三角形ABCの内側にDがあるか？
・三角形BCDの内側にAがあるか？
・三角形CDAの内側にBがあるか？
・三角形DABの内側にCがあるか？
上記のどれか一つでも成り立っていれば「No」、全部成り立っていなければ「Yes」です。

ある点が三角形の内側にあるか？を確認する方法はほとんどの人が知らないでしょう。こういうときはググりましょう。
「三角形 内側 点 python」でググれば頭のいい人がコードを公開してくれています。
【提出】では外積を使う方法を紹介しています。何をしているのかの直感的な理解は以下の記事がわかりやすいと思います。
https://qiita.com/progfay/items/dfeb8c4ff6ab5738b6e7
より厳密な証明が知りたいという人は「三角形 外積 内部」とかでググればでてくるでしょう。

【提出】

# 入力の受け取り
A=list(map(int,input().split()))
B=list(map(int,input().split()))
C=list(map(int,input().split()))
D=list(map(int,input().split()))

#点abのベクトル
def vec(a,b):
    # ベクトルを返す
    return (a[0]-b[0],a[1]-b[1])

#三角形abcの内部に点pがあるか確認する
# 内部ならTrueを返す
def InTrianble(a,b,c,p): 

    # それぞれのベクトルを計算
    ab=vec(b,a)
    bp=vec(p,b)

    bc=vec(c,b)
    cp=vec(p,c)

    ca=vec(a,c)
    ap=vec(p,a)

    #外積(Outer Product)を求める
    OP1=ab[0]*bp[1]-ab[1]*bp[0]
    OP2=bc[0]*cp[1]-bc[1]*cp[0]
    OP3=ca[0]*ap[1]-ca[1]*ap[0]

    #外積の向き　正負がそろっていれば内側
    if (OP1>0 and OP2>0 and OP3>0) or (OP1<0 and OP2<0 and OP3<0):
        return True

# 三角形ABCの内側にDがあるか？
# 三角形BCDの内側にAがあるか？
# 三角形CDAの内側にBがあるか？
# 三角形DABの内側にCがあるか？
if InTrianble(A,B,C,D)==True or InTrianble(B,C,D,A)==True or InTrianble(C,D,A,B)==True or InTrianble(D,A,B,C)==True:
    # 「No」を出力
    print("No")
# 上記全て成り立たない
else:
    # 「Yes」を出力
    print("Yes")

D - Snuke Panic (1D)　Dif:840

DPで解きます。

DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。

DPの解説動画を作りましたので、本問が難しいと感じた方は是非御覧ください。

具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する

以下を例に考えます。
4
1 1 3
2 2 5
3 4 6
5 2 8

(1)表を作る
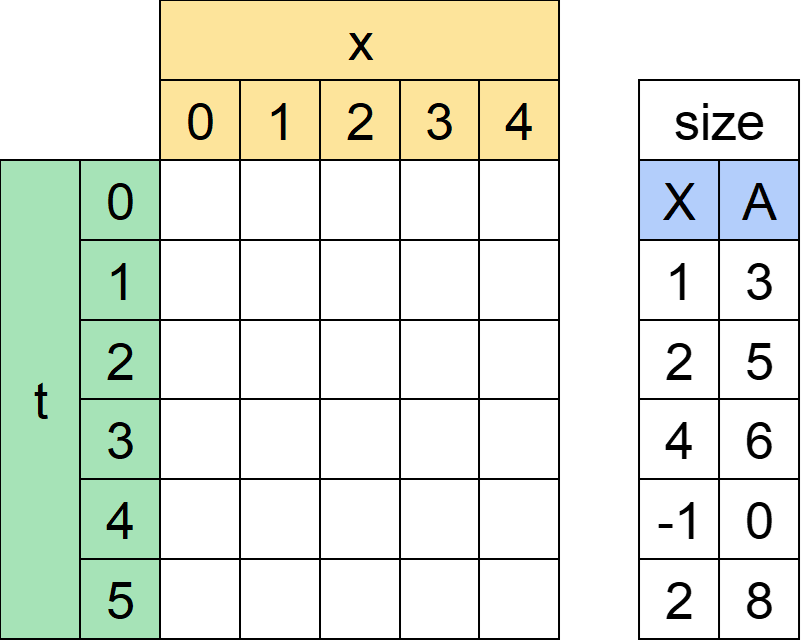
今回作る表は以下です。
「時刻t時点で座標xにいる場合、捕まえたすぬけ君の大きさ合計最大値」
表の名前はdpとします。
例えばdp[3][1]=8ならば「時刻3時点で座標1にいる」という前提で捕まえうるすぬけ君の大きさ合計最大値が8であるという意味になります。

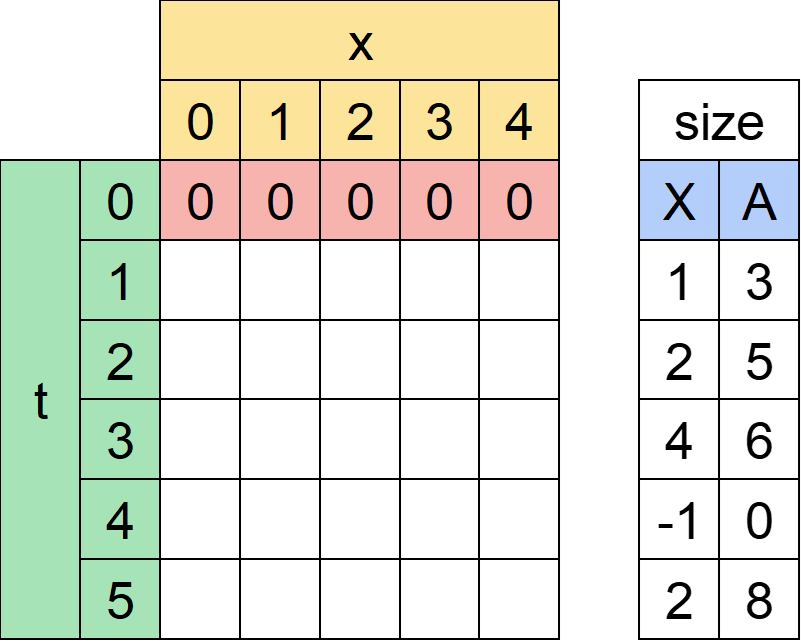
(2)すぐにわかるところを埋める
すぐにわかるのはt=0の行です。時刻0時点で捕まえることができるすぬけ君はいないので全て0になります。

(3)表の小さい方から答えにたどり着くまで埋める
t=1の行を考えましょう。
t=1時点では座標1に大きさ3のすぬけ君が出ています。よってt=1の時点で座標1にいる場合のみ捕まえることができ、dp[1][1]=3となります。
それ以外の箇所で捕まえることはできないので0です。

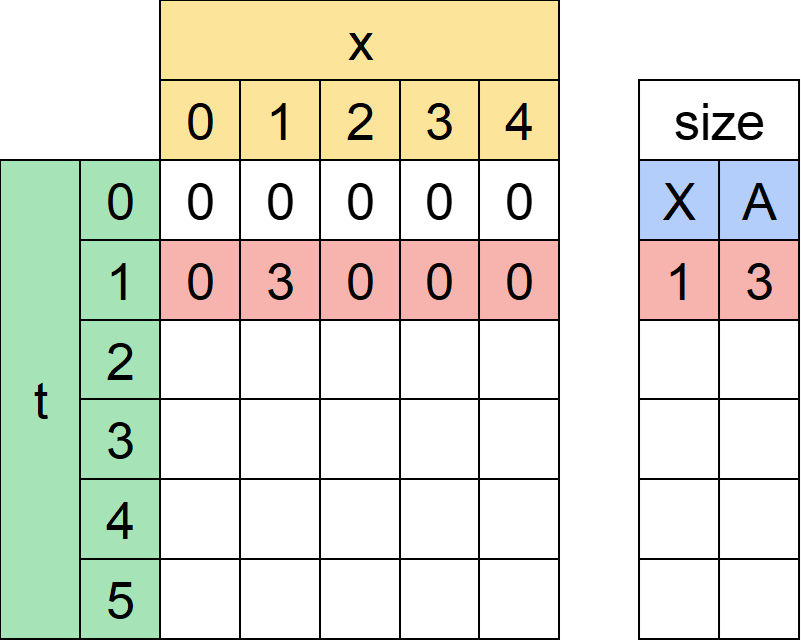
t=2の行はどうなるでしょうか。重要なのは時刻1→2になる間で進める距離は1ということです。
つまりt=1でx=1にいたならば次に進めるのはx=0,1,2のどれかで、x=4にいたならば次に進めるのはx=3,4のどちらかということになります。
例えばdp[2][1]については時刻t=1でx=0,1,2のどれかにいる状態から移動が可能です。当然すぬけ君を捕まえた後に座標1へ移動するのが最適です。
つまり上の行の左上、上、右上のうち、最も大きいものをそのまま埋めれば良いということになります。

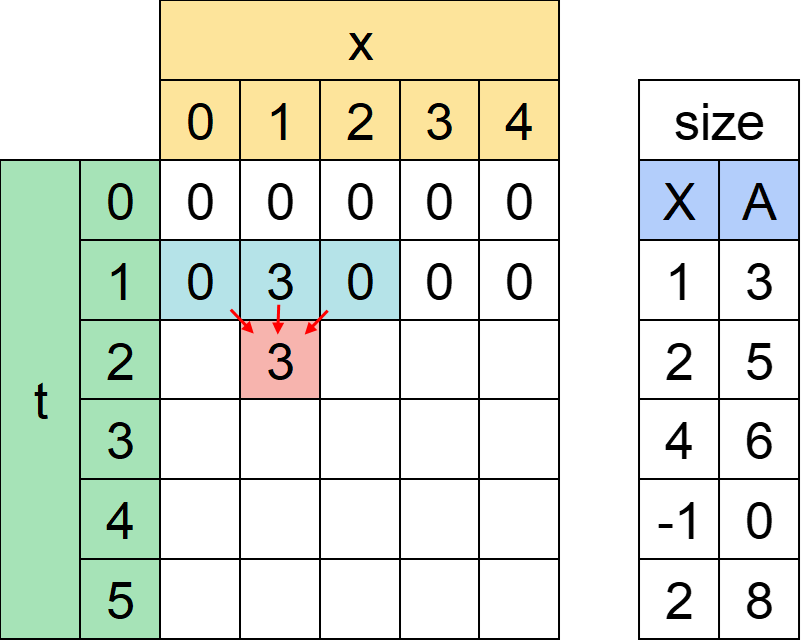
一般には以下のようになります。
dp[i][0]=max(dp[i-1][0],dp[i-1][1])
dp[i][1]=max(dp[i-1][0],dp[i-1][1],dp[i-1][2])
dp[i][2]=max(dp[i-1][1],dp[i-1][2],dp[i-1][3])
dp[i][3]=max(dp[i-1][2],dp[i-1][3],dp[i-1][4])
dp[i][4]=max(dp[i-1][3],dp[i-1][4])
更に時刻2では座標2に大きさ5のすぬけ君がいます。よってdp[2][2]だけ捕まえることができ、+5する必要があります。

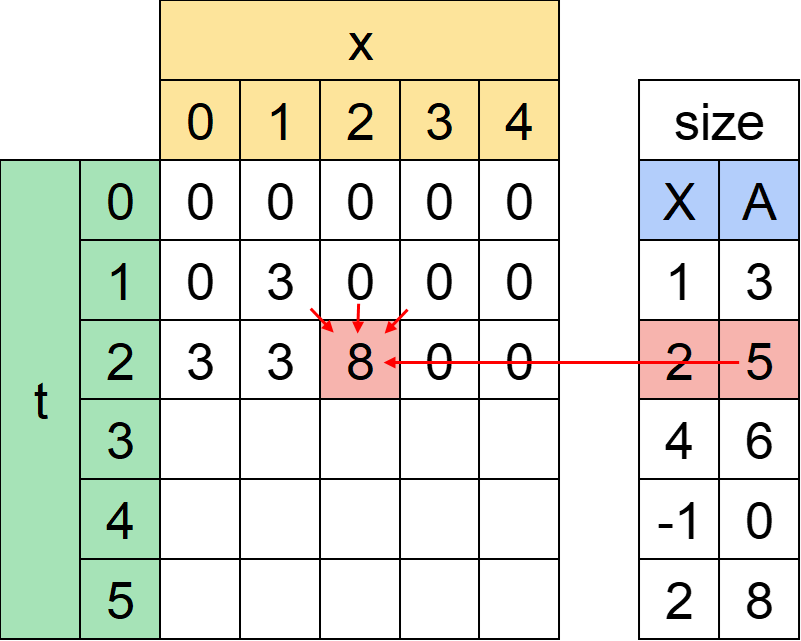
同様にして表を全部埋めればいいのですが、注意点が一つあります。
時刻t=3時点に座標4に大きさ6のすぬけ君がいますがこれは足してはいけません。
どう頑張っても時刻3に座標4へたどり着けないからです。

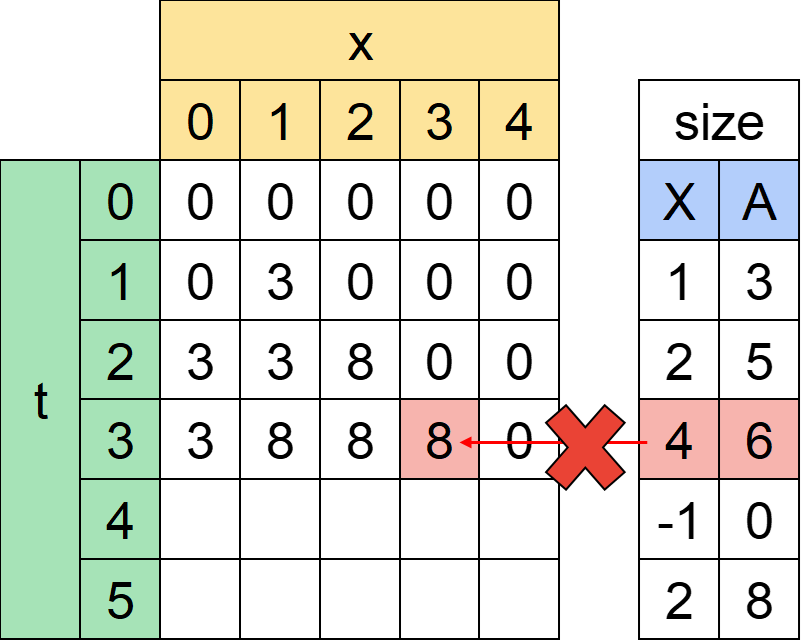
ちなみに時刻4にはすぬけ君はでてきませんが、実装を楽にするために座標-1に大きさ0のすぬけ君が出現するというように記録しています。

(4)答えを出力する
表を全部埋めると以下のようになります。

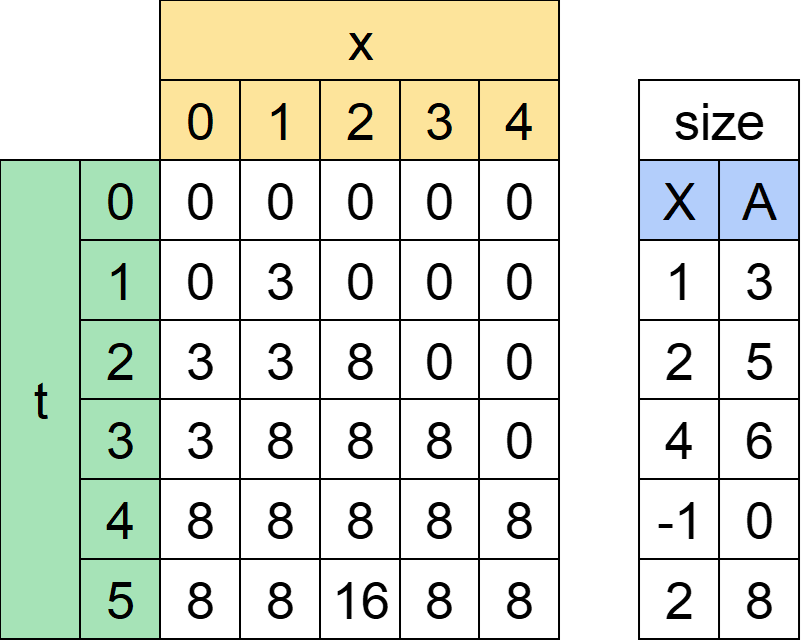
t=5の行は「時刻5時点で座標xにいる場合、捕まえたすぬけ君の大きさ合計最大値」を表します。
最後どこにいても構わないのでこの行の最大値、16が最終的な答えになります。
実装では(Tの最大値)行の表を作ればいいのですが、面倒なのでとりあえずTの最大値10^5行の表を作って埋めてしまえばいいでしょう。

【提出】

# 入力の受け取り
N=int(input())

# すぬけ君のでるタイミングと大きさを記録
# Size[T]=[X,A]の形で記録する
# 出てこない時刻は[-1,0]と記録
Size=[[-1,0] for i in range(10**5+1)]

# N回
for i in range(N):
	# 入力の受け取り
    T,X,A=map(int,input().split())
	# T秒時点で座標Xに大きさAのすぬけ君が出ると記録
    Size[T]=[X,A]

# (1)表を作る
# (2)すぐにわかるところを埋める
dp=[[0,0,0,0,0] for i in range(10**5+1)]

# (3)表の小さい方から答えにたどり着くまで埋める
# t=1~10^5
for t in range(1,10**5+1):
    # 左上、上、右上のうち一番大きいものを埋める
    dp[t][0]=max(dp[t-1][0],dp[t-1][1])
    dp[t][1]=max(dp[t-1][0],dp[t-1][1],dp[t-1][2])
    dp[t][2]=max(dp[t-1][1],dp[t-1][2],dp[t-1][3])
    dp[t][3]=max(dp[t-1][2],dp[t-1][3],dp[t-1][4])
    dp[t][4]=max(dp[t-1][3],dp[t-1][4])

    # X,Aを取り出し
    X,A=Size[t]
    # Xga-1でない かつ X≤tである(t時点でたどり着ける)
    if X!=-1 and X<=t:
        # 捕まえられるすぬけ君を足す
        dp[t][X]+=A

# (4)答えを出力する
# 10**5行の最大値を出力
print(max(dp[10**5]))

【広告】

『AtCoder 最速で緑になる 基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312