はじめに
三角形は素晴らしいです。この記事では回転方向から三角形と点の内外判定までを説明します。(数学的な話がありますが、本当に正しいかどうかは保証できませんのでご了承ください...)
時計回りか反時計回りか
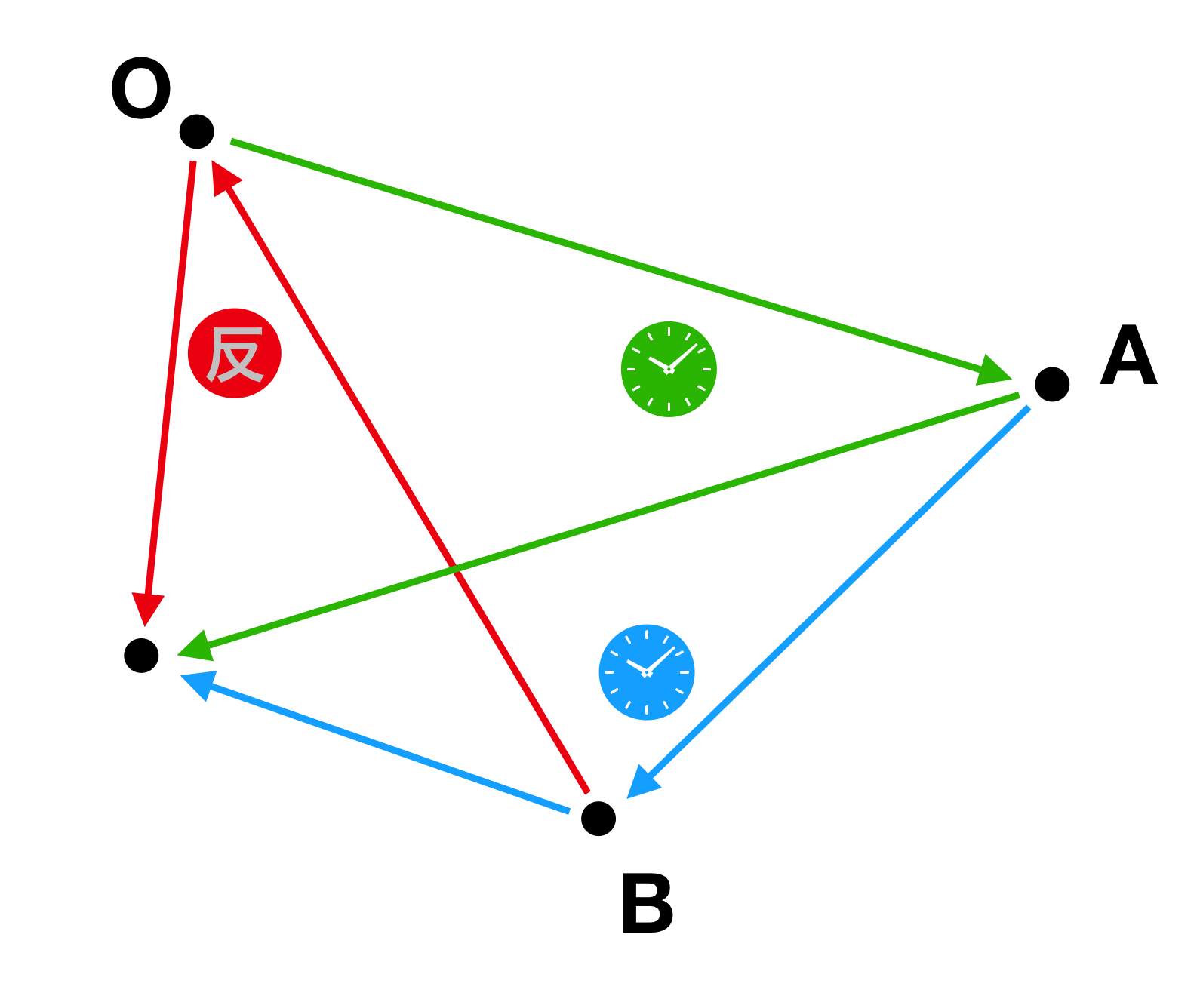
2次元平面上の一直線上に並んでいない3点を順番に結ぶと、それは時計回りか反時計回りかのどちらかに区別することができます。点O, A, Bを O → A → B の順で結ぶと時計回りで、 O → B → A の順で結ぶと反時計回りとなります。
ベクトルの外積
ここで、いきなりですがベクトルの外積について覚えていますか?
$$(a_x, a_y, a_z) \times (b_x, b_y, b_z) = (a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y-a_yb_x)$$
$$\big| \vec{a} \times \vec{b} \big| = \big|\vec{a}\big|\big|\vec{b}\big| \cdot \big|\sin\theta\big|$$
また、外積は2つのベクトルに対して直交するベクトルを得られることでも知られています。よって、XY平面上に限るなら以下のようにも言い換えられます。
$$\vec{a} \times \vec{b} = \big(0, 0, \big|\vec{a}\big|\big|\vec{b}\big|\sin\theta \big)$$
ここで $\theta$ の範囲は $0$ から $2\pi$ (もしくは $-\pi$ から $\pi$ )です。 $\sin\theta$ は $\theta \in (0, \pi)$ で正、 $\theta \in (\pi, 2\pi)$ で負を取るため、外積のzの値から $\theta$ が $(0, \pi)$ か $(\pi, 2\pi)$ 、または $0, \pi$ のどれに属しているかを判定することができます。 (0のときは $0, \pi$ のどちらか)
θはなにを示しているのか
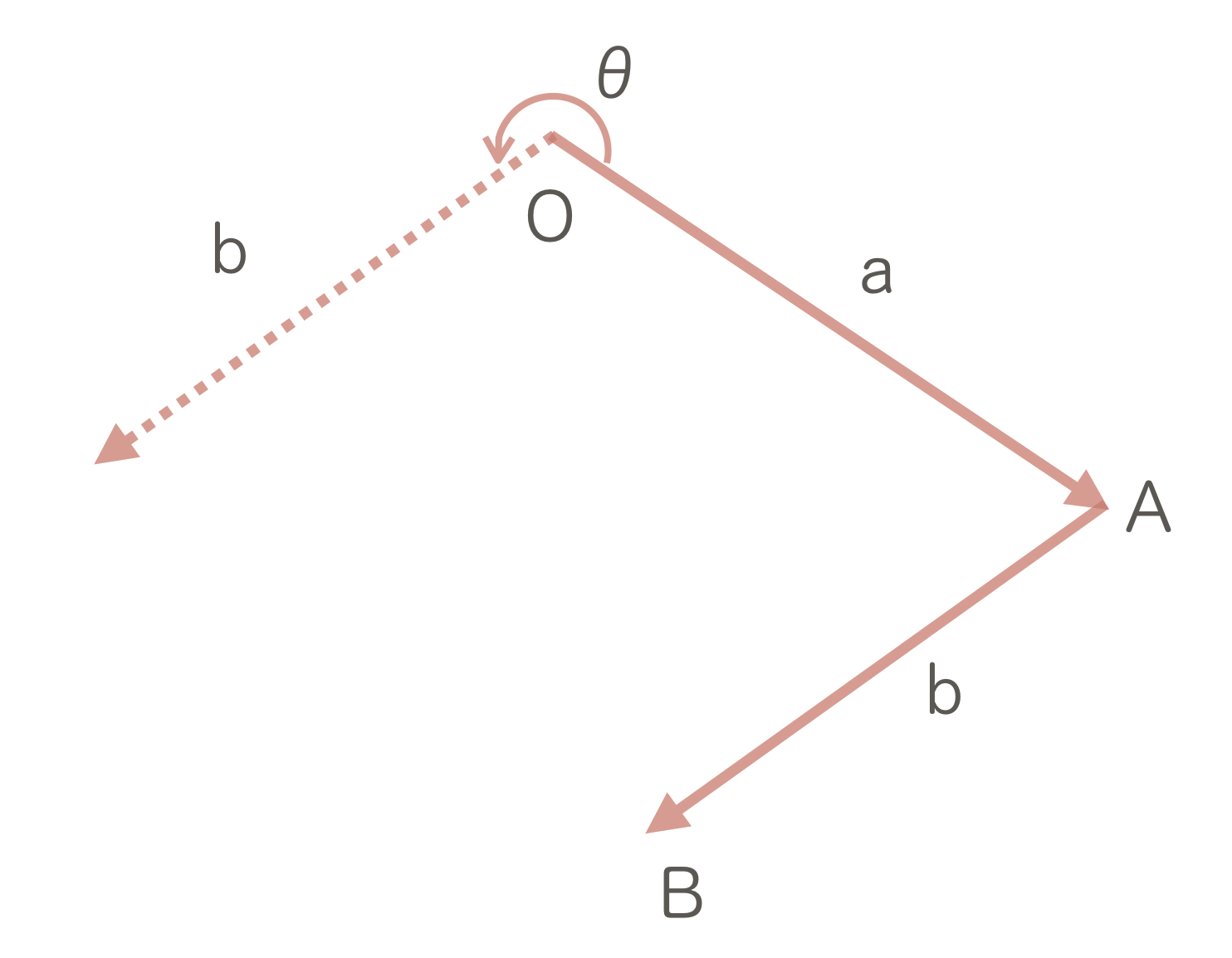
この画像は $\vec{OA} \times \vec{AB}$ における $\theta$ を表した図です。$\theta$ とは、始点を原点に移動した際の $\vec{OA}$ から $\vec{AB}$ へ 反時計回りを正とする回転角 のことを指します。
なぜ反時計回りなのかというと、別に時計回りでも問題はありません。みなさんが高校時代に勉強した三角関数もxy座標軸に対して反時計回りを正として考えていました。これは座標系が右手系であるからです。座標系が左手系である場合は時計回りを正とすればいいのです。
時計回りと反時計回りの違い
ここで、時計回りと反時計回りはどのような違いがあるのかについて考えてみましょう。答えは簡単です。 $\theta$ が $(0, \pi)$ の範囲内か $(\pi, 2\pi)$ の範囲内であるか ( $0, \pi$ のときは一直線に並ぶ) です。左手系ならば、 $\theta \in (0, \pi)$ で時計回り、 $\theta \in (\pi, 2\pi)$ で反時計回りであり、右手系ならばその逆です。実際に紙に書いて確かめてみるとわかりやすいでしょう。
判定
ここまでの話から、点を結んだ順路は外積によって時計回りか反時計回りかを判定することができそうです。時計回りである O → A → B の順で結んだ場合について考えます。
$\vec{OA} \times \vec{AB}$ について、 $\theta \in (0, \pi)$ (見た目から判断してます😅) と考えられるでしょう。すなわち時計回りです。外積のzの値は $\big|\vec{a}\big|\big|\vec{b}\big|\sin\theta$ であることから、正であると言えます。
つまり、左手系のXY平面上の順路 O → A → B について、 $\vec{OA} \times \vec{AB}$ のzの値が正ならば時計回り、負ならば反時計回り (0ならば一直線に並んでいる) ということがわかりました。
三角形と点の内外判定
ここまでを理解できたあなたならば、この記事がどのように内外判定を行えているのかを理解することができるでしょう。
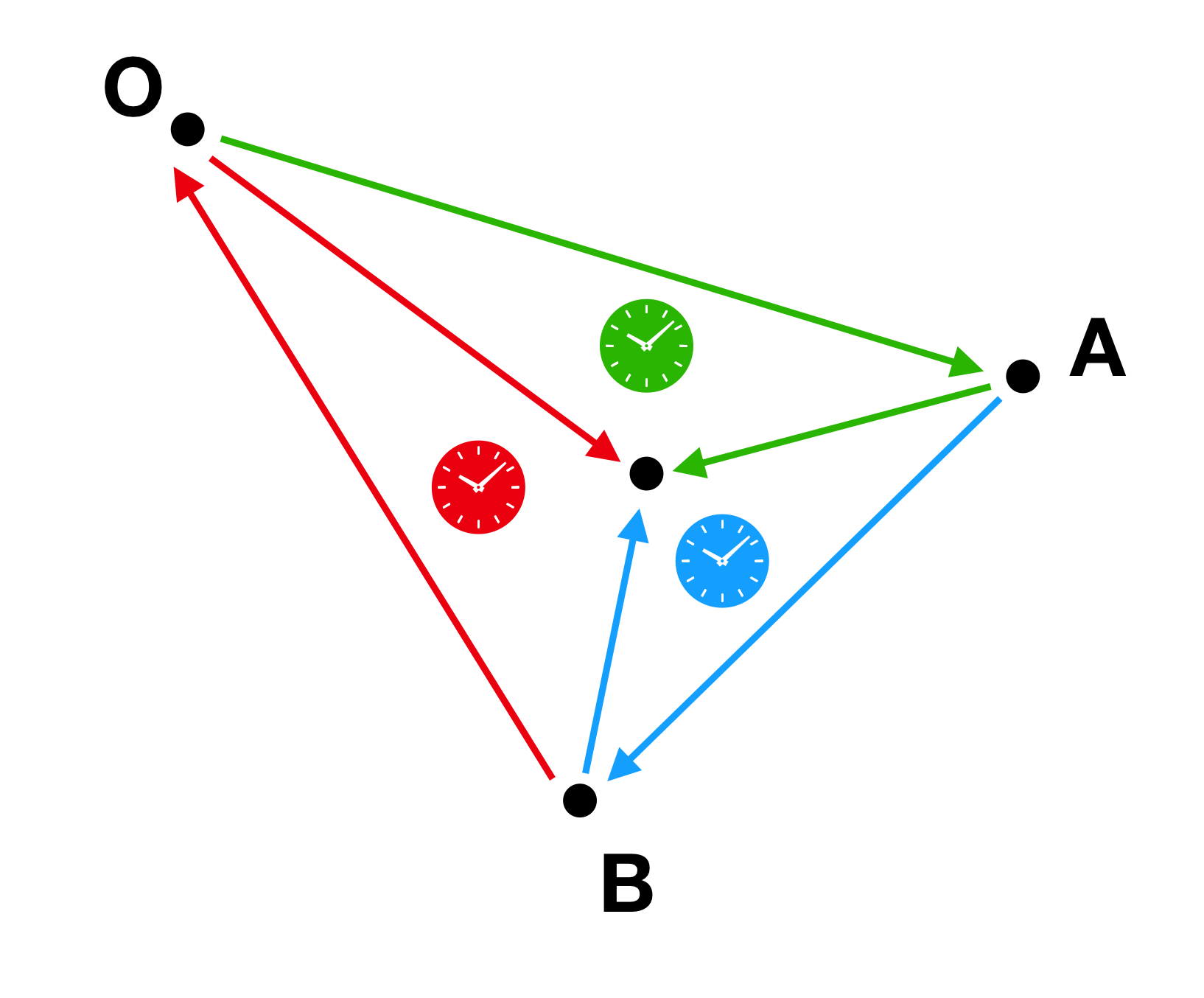
このように点が内側にあるときは、赤と緑、青色の順路の回転方向が一致します。
このように点が外側にあるときは、順路の回転方向が一致しないということです。よって外積によって求めるということができるのです。
おわりに
以上、外積と回転方向の関係性について学びました。今回はXY平面上に限ってしまいましたが、3次元平面上の3点に対してそのすべてを含む平面は一意に決定するため、このお話を3次元に拡張することが可能だと思います。(めんどくさいので証明とかはしてません)