ABC244(AtCoder Beginner Contest 244)　A～E問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Last Letter

Sを受け取って末尾の文字を出力します。

Sの末尾、つまり右から1文字目はS[-1]と書けば確認できます。
よってS[-1]を出力すればOKです。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
N=int(input())
S=input()

# Sの右から1文字目を出力
print(S[-1])

B - Go Straight and Turn Right

今いる座標と向いている方向を管理します。
今いる座標が(x,y)である場合
東向きに進む：(x+1,y)
南向きに進む：(x,y-1)
西向きに進む：(x-1,y)
北向きに進む：(x,y+1)
となるのでそれぞれ条件分岐をすればOKです。

「R」が来たら向きが変わるのでそれも条件分岐を使って行います。

【提出】

# 入力の受け取り
N=int(input())
T=input()

# 方向：最初は東
direct="East"

# 今いる座標
now=[0,0]

# i=0~(N-1)
for i in range(N):
    # T[i]=「S」のとき
    if T[i]=="S":
        # 今のx座標
        now_x=now[0]
        # 今のy座標
        now_y=now[1]

        # 東向きの場合
        if direct=="East":
            now=[now_x+1,now_y]
        # 南向きの場合
        elif direct=="South":
            now=[now_x,now_y-1]
        # 西向きの場合
        elif direct=="West":
            now=[now_x-1,now_y]
        # 北向きの場合
        elif direct=="North":
            now=[now_x,now_y+1]
    
    # T[i]=「R」の場合
    else:
        # 方向を変える
        if direct=="East":
            direct="South"
        elif direct=="South":
            direct="West"
        elif direct=="West":
            direct="North"
        elif direct=="North":
            direct="East"

# 答えの出力
print(now[0],now[1])

C - Yamanote Line Game

Nが小さいので、入力を受け取る度まだ使っていない整数を確認して出力すればOKです。
usedという配列を用意し、最初はすべて「False」にしておきます。

一番最初は「1」を宣言し、「1」を使用済み⇔used[1]=Trueに変更します。
青木くんの宣言した数字を受け取ったらそれもusedをTrueに変更します。
used[1],used[2],...についてまだFalseのものを探し、Falseがあればそれを宣言し、Trueに変更します。

青木くんから「0」が入力されたらプログラムを終了します。
『出力を行うたびに標準出力をflushしてください。』とありますがpythonでは特に気にしなくても問題ありません。

【提出】

# 入力の受け取り
N=int(input())

# すでに使った数の記録
used=[False]*(2*N+2)

# 最初は「1」を出力
print(1)
# 「1」は使用済み
used[1]=True

# N回
for i in range(N+1):
    # 青木くんの入力を受け取り
    x=int(input())
    # 「x」は使った
    used[x]=True

    # x=「0」の場合
    if x==0:
        # 終了
        exit()
    
    # k=1~(2k+1)
    for k in range(1,2*N+2):
        # まだ使っていないなら
        if used[k]==False:
            # 「k」を出力
            print(k)
            # 「k」は使った
            used[k]=True
            # forループを抜ける
            break

D - Swap Hats

S,Tのパターンは以下の3種類です。
(1)3色すべて同じ位置
(2)1色のみ同じ位置で2色は逆
(3)すべて違う位置

(1)は入力例の通り、どれか2つを選んで10^18回操作を行えばS,Tを同じ並びにできます。
(2)は同じ並びにできません。
(3)適切な入れ替えを2回行うことで(1)と同じパターンにできます。よってS,Tを同じ並びにできます。

(2)が達成不可能なことは公式解説のように考えることで証明できますが、コンテスト中は「このパターンはなんとなく無理そうだなー」程度でとりあえず提出してしまえばいいでしょう。

【提出】

# 入力の受け取り
S1,S2,S3=map(str,input().split())
T1,T2,T3=map(str,input().split())

# (1)3色すべて同じ位置
if S1==T1 and S2==T2 and S3==T3:
    print("Yes")
# (2)1色のみ同じ位置で2色は逆
elif S1==T1 or S2==T2 or S3==T3:
    print("No")
# (3)すべて違う位置
else:
    print("Yes")

E - King Bombee

この問題はDP問題の中でも特に難易度が高いです。DPをあまり解いたことがない人は先に簡単なDP問題を解いてみることをおすすめします。
以下が比較的簡単なDP問題です。
ABC211C：https://atcoder.jp/contests/abc211/tasks/abc211_c
解説：https://qiita.com/sano192/items/051207b6607b56cc439e#c---chokudai
ABC222D：https://atcoder.jp/contests/abc222/tasks/abc222_d
解説：https://qiita.com/sano192/items/e42b9861ece2c339394a#d---between-two-arrays
その他のDP問題も演習したい人は「ものすごく丁寧でわかりやすいABC解説一覧」の「逆引き DP」を御覧ください。
https://qiita.com/sano192/items/54accd04df62242b70f0#%E9%80%86%E5%BC%95%E3%81%8D

DPで解きます。

DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。

具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する

DPの解説動画を作りましたので、本問が難しいと感じた方は是非御覧ください。
https://www.youtube.com/watch?v=gVJ16ThsJYs

入力例1を例として考えましょう。
N M：4 4
K：4
S T：1 3
X：2
U1 V1：1 2
U2 V2：2 3
U3 V3：3 4
U4 V4：1 4

グラフは以下のようになります。

(1)表を作る
今回作る表は「i回の移動でjにたどり着く方法のうち、Xを偶数回/奇数回通る方法の数」とします。
表の名前はdpとします。(dp[i][j][偶/奇])

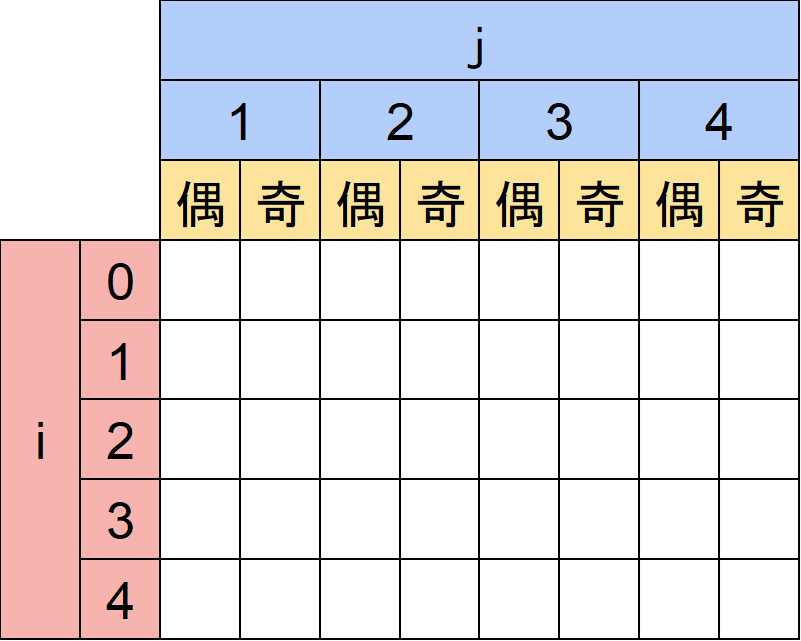
例えばdp[2][3][偶]であれば「2回の移動で③にたどり着く方法のうち、②を偶数回通る方法の数」となります。
2回の移動で③にたどり着く方法は
①→②→③
①→④→③
の2通りでそのうち②を偶数回(0回)通っているのは①→④→③のみなのでdp[2][3][偶]=1となります。

最終的には「K回の移動でTにたどり着く方法のうち、Xを偶数回通る方法の数」が答えなのでdp[K][T][偶]が埋まれば終わりです。

(2)すぐにわかるところを埋める
すぐに分かるところは移動回数が0、すなわち0行目です。
0回の移動で到達できるのはスタート地点であるSのみです。また、X≠Sという条件があるのでXを通る回数は必ず0回=偶数になります。
よってdp[0][S][偶]=1となります。
0行目の他の箇所は到達しようがないのですべて0になります。

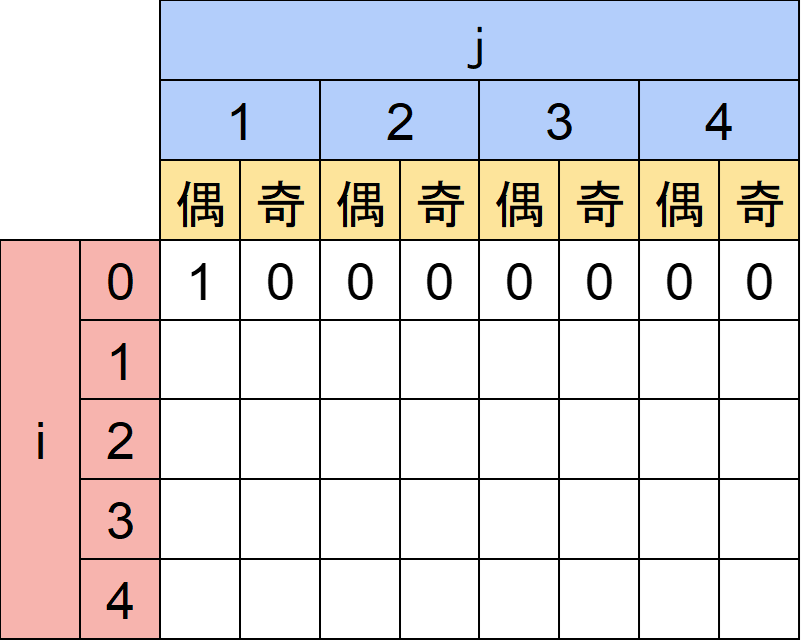
(3)表の小さい方から答えにたどり着くまで埋める
1回移動してたどり着ける場所を考えましょう。
0回の移動で①にたどり着けることはわかりました。①から行ける場所は②、④の2箇所です。
・①→②：0回の移動で①にたどり着く方法は1通りでした。よってそこから②にたどり着く方法も1通りです。更に②を一度通るので②を通る回数が1回増え、奇数回となります。まとめるとdp[1][2][奇]=1となります。
・①→④：同様に④にたどり着く方法も1通りです。②は通らないので②を通る回数は変わらず0回となります。まとめるとdp[1][4][偶]=1となります。

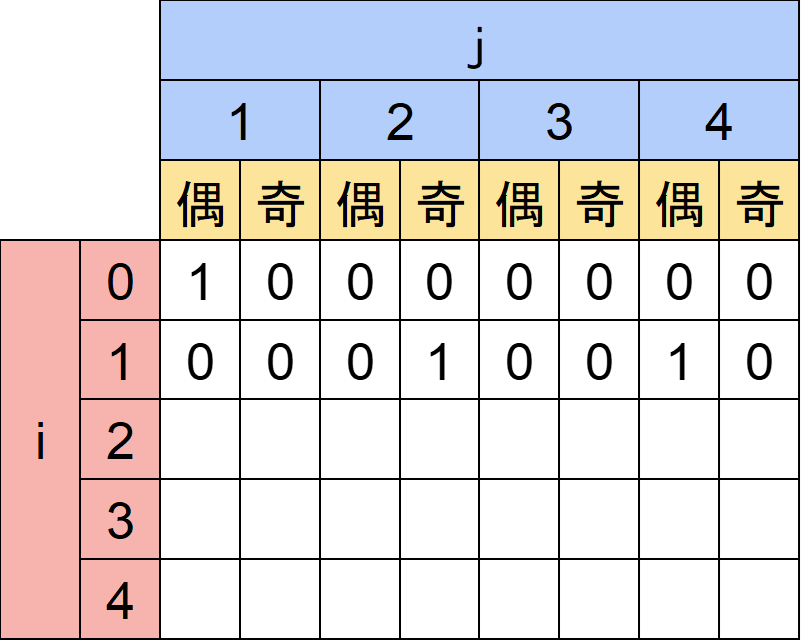
この移動を一般化して考えてみましょう。
UとVが行き来可能な場合、(i-1)回の移動でUにたどり着く方法の数がわかっていれば、そこから1回移動してVにたどり着く方法は単純に足し算をすればよいです。
この時、行き先V=XであればXを通る回数が増える=偶奇が入れ替わります。そうでない場合は偶奇は同じです。
V=Xの場合
dp[i][V][偶]+=dp[i-1][U][奇]
dp[i][V][奇]+=dp[i-1][U][偶]
V≠Xの場合
dp[i][V][偶]+=dp[i-1][U][偶]
dp[i][V][奇]+=dp[i-1][U][奇]
これをi=1~Kについて、すべてU,Vの組(U→V,V→U)について計算します。

(4)答えを出力する
表をすべて埋めると以下のようになります。

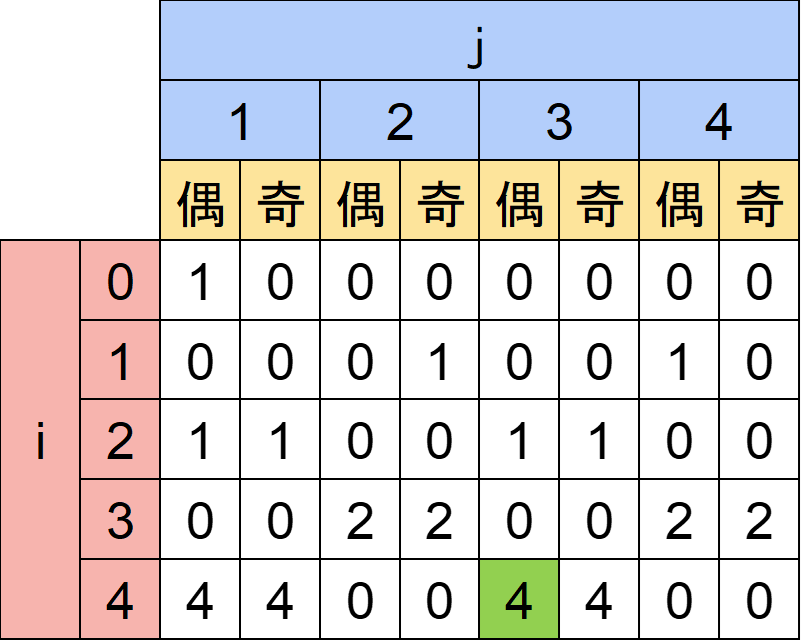
答えはdp[K][T][偶]=dp[4][3][偶]=4になります。

実装については3次元の配列が必要です。3次元配列は以下のように作ります。
dp=[[[0,0] for i in range(N+1)] for j in range(K+1)]

dp[1番目の要素][2番目の要素][3番目の要素]としたいなら
dp=[[[0]*(3番目の要素数) for i in range(2番目の要素数)] for j in range(1番目の要素数)]
というように並びが逆になると覚えておけばよいです。

説明ではdp[i][j][偶],dp[i][j][奇]というようにしましたが、実装では偶=0,奇=1としています。

pythonでは間に合わないのでpypyで提出します。

【提出】

# pypyで提出

# 余りの定義
mod=998244353

# 入力の受け取り
N,M,K,S,T,X=map(int,input().split())

# (1)表を作る
# 「i回の移動でjにたどり着く方法のうち、Xを偶数回/奇数回通る方法の数」
dp=[[[0,0] for i in range(N+1)] for j in range(K+1)]

# 辺の格納
edge=[]
# M回
for i in range(M):
    # 入力の受け取り
    U,V=map(int,input().split())
    # 辺の記録
    edge.append([U,V])

# (2)すぐにわかるところを埋める
dp[0][S][0]=1

# (3)表の小さい方から答えにたどり着くまで埋める
# i=1~K
for i in range(1,K+1):
    # 各辺の組について
    for U,V in edge:        
        # U→V
        # V=Xの場合⇔Xを通る回数が増える⇔偶奇が入れ替わる
        if V==X:
            dp[i][V][0]+=dp[i-1][U][1]
            dp[i][V][1]+=dp[i-1][U][0] 
        # V≠Xの場合⇔Xを通る回数が増えない⇔偶奇は同じ
        else:                
            dp[i][V][0]+=dp[i-1][U][0]
            dp[i][V][1]+=dp[i-1][U][1]
        # 余りを取る
        dp[i][V][0]%=mod
        dp[i][V][1]%=mod

        # V→U
        # U=Xの場合⇔Xを通る回数が増える⇔偶奇が入れ替わる
        if U==X:
            dp[i][U][0]+=dp[i-1][V][1]
            dp[i][U][1]+=dp[i-1][V][0]
        # U≠Xの場合⇔Xを通る回数が増えない⇔偶奇は同じ
        else:                
            dp[i][U][0]+=dp[i-1][V][0]
            dp[i][U][1]+=dp[i-1][V][1]
        # 余りを取る
        dp[i][U][0]%=mod
        dp[i][U][1]%=mod

# (4)答えを出力する
print(dp[K][T][0])

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737