エクサウィザーズプログラミングコンテスト2021(ABC222) A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

エクサウィザーズプログラミングコンテスト2021　A～D問題の解説記事です。
(ABC222(AtCoder Beginner Contest 222))
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

株式会社エクサウィザーズ様について

AIを使った社会課題解決をされている企業様です。
興味のある方は上記採用情報を御覧ください。

A - Four Digits

入力を受け取り、桁数を確認して必要な分"0"を追加して出力します。
コツは数値ではなく文字列として受け取ることです。
文字列として受け取ることで
len(N)
として文字数=桁数が確認できます。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り(文字列)
N=input()

# 桁数
disit=len(N)

# 桁数が1なら
if disit==1:
    # 先頭に"000"をつけて出力
    print("000"+N)
# 桁数が2なら
if disit==2:
    # 先頭に"00"をつけて出力
    print("00"+N)
# 桁数が3なら
if disit==3:
    # 先頭に"0"をつけて出力
    print("0"+N)
# 桁数が4なら
if disit==4:
    # そのまま出力
    print(N)

B - Failing Grade

aの各要素についてP未満かを順に確認します。
P未満の人数を数えて出力すれば終わりです。

【提出】

# 入力の受け取り
N,P=map(int, input().split())
a=list(map(int, input().split()))

# 答えを格納する変数
ans=0

# i=0~N-1まで
for i in range(N):
    # a[i]がP未満なら
    if a[i]<P:
        # 答えにプラス1
        ans+=1

# 答えを出力
print(ans)

C - Swiss-System Tournament

制約が小さいので全ての試合をシュミレーションすればよいです。
やることがそれなりに多いので、実装するのは大変ですが頑張りましょう。

以下の手順で実装します、
(1)手の入力を0インデックスで記録する(hand)
　※0インデックスなので
　選手1の1ラウンドの目の手=hand[0][0]
　選手1の2ラウンドの目の手=hand[0][1]
　選手1の3ラウンドの目の手=hand[0][2]
　...
　選手2の1ラウンドの目の手=hand[1][0]
　...
　と選手番号とラウンドの番号が1つずつずれることに注意してください。
(2)選手の勝数と番号を記録するリストを用意(wins)
　※コツは[選手の勝数,選手番号]の順に記録することです。
　後に勝数順にソートするため、勝数がリストの1番目の要素としてあったほうが楽に実装できます。
(3)Aの手,Bの手を引数→Aの追加勝数,Bの追加勝数を返す関数を作る
　勝ったら+1、引き分け、負けたら+0
(4)Mラウンドの試合を行う
　順位：2k→選手A
　順位：2k+1→選手B
　として選手Aと選手Bの試合結果を確認する
　※問題文では「2k-1」と「2k」が試合となっていますが0インデックスにしたため、番号がずれています。
(5)追加勝数をwinsにマイナスで記録する
　例：選手0が2勝していたら[-2,0]となる
　※マイナスで記録するのは後のソートを楽にするためです。
(6)winsを勝数,選手番号順にソートする
　※wins.sort()とすることで　「1番目の要素」=「勝数」昇順→「2番目の要素」=「選手番号」昇順　に並び替えができます。
　この時並び替えを「1番目の要素」「2番目の要素」ともに昇順で並び替えるため、勝数をマイナスで記録しています。
　(勝数をプラスで記録すると　「1番目の要素」=「勝数」降順→「2番目の要素」=「選手番号」昇順　に並び替えが必要となり、実装が非常にめんどくさいことになります)
(7)答え(winsの2番目の要素)を出力する

【提出】

# 入力の受け取り
N,M=map(int, input().split())

# 手の記録用
hand=[]

# 2N回受け取り
for i in range(2*N):
    # 受け取り
    A=input()
    # 記録
    hand.append(A)
# [勝数,選手番号]を格納するリスト
# 選手番号は0インデックス(選手1は0,選手2は1,...)
wins=[]

# 全員0で初期化
for i in range(2*N):
    wins.append([0,i])

# 試合の結果判定
# 引数；選手Aの手,選手Bの手→選手Aの追加勝数,選手Bの追加勝数を返す
def match(A_hand,B_hand):
    if A_hand=="G" and B_hand=="G":
        return 0,0
    elif A_hand=="G" and B_hand=="C":
        return 1,0
    elif A_hand=="G" and B_hand=="P":
        return 0,1
    if A_hand=="C" and B_hand=="G":
        return 0,1
    elif A_hand=="C" and B_hand=="C":
        return 0,0
    elif A_hand=="C" and B_hand=="P":
        return 1,0
    if A_hand=="P" and B_hand=="G":
        return 1,0
    elif A_hand=="P" and B_hand=="C":
        return 0,1
    elif A_hand=="P" and B_hand=="P":
        return 0,0

# Mラウンド(0インデックス,i=0~M-1まで)
for i in range(M):
    # k=0~N-1まで
    for k in range(N):
        # 順位2kと(2k+1)の試合
        # 選手Aの番号(0インデックス)
        playerA=wins[2*k][1]
        # 選手Bの番号(0インデックス)
        playerB=wins[2*k+1][1]
        # 選手Aの出す手
        A_hand=hand[playerA][i]
        # 選手Bの出す手
        B_hand=hand[playerB][i]
        # A,Bに追加される勝数
        A_point,B_point=match(A_hand, B_hand)
        # Aの勝数を計算(勝ったらマイナス1)
        wins[2*k][0]-=A_point
        # Bの勝数を計算(勝ったらマイナス1)
        wins[2*k+1][0]-=B_point
    # 勝数,番号順にソート
    wins.sort()

# i=0~2Nまで
for i in range(2*N):
    # 答えの出力
    # 選手番号は0インデックスなのでプラス1して戻す
    print(wins[i][1]+1)

D - Between Two Arrays

DPを使います。

DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。

具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する

例えば以下の入力を例として考えます。
N：4
A：1 2 3 4
B：5 6 7 8

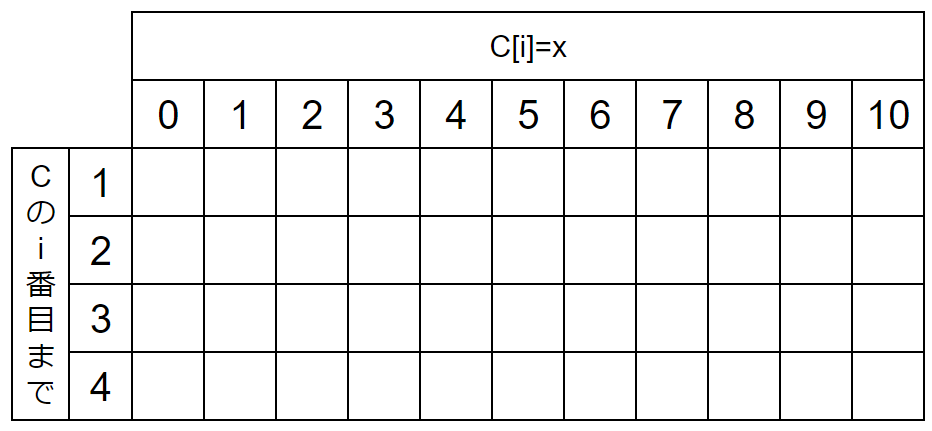
(1)表を作る
今回作る表は
『Cのi番目まででC[i]がxであるような数列の個数』
とします。
表の名前はdpとします。

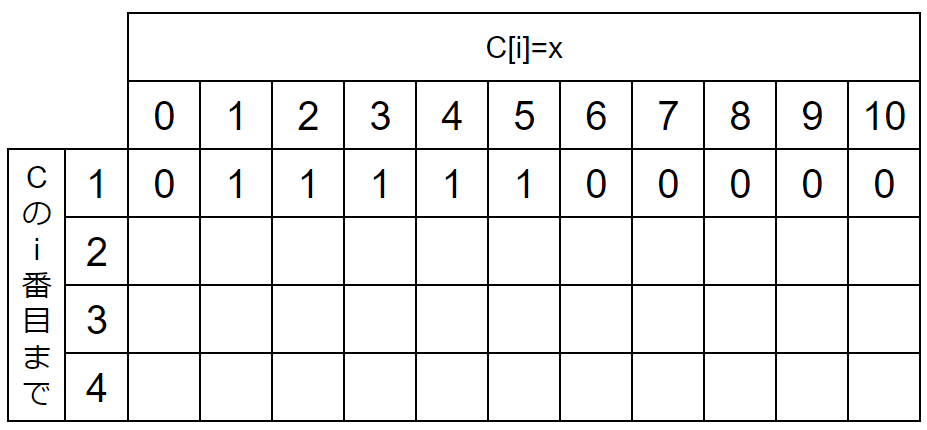
本当はx=3000(B[i]の最大値)まで必要ですが見やすいようにx=10までで作ります。

dp[2][3]であれば
『Cの2番目まででC[2]が3であるような数列の個数』
を表します。考えられるのは以下です。
C=(1,3),(2,3),(3,3)
ゆえにdp[2][3]=3となります。

(2)すぐにわかるところを埋める
すぐにわかるのは1行目(i=1)です。
i=1は
『Cの1番目まででC[1]がxであるような数列の個数』
を表します。
dp[1][1]=1（作れる数列C:(1))
dp[1][2]=1（作れる数列C:(2))
dp[1][3]=1（作れる数列C:(3))
dp[1][4]=1（作れる数列C:(4))
dp[1][5]=1（作れる数列C:(5))
となります。
それ以外の箇所はA[1]≦x≦B[1]でなく、「C[1]がxである」が満たせないので数列が作れません。ゆえに0です。
一般に考えるとx=A[1]~B[1]について
dp[1][x]=1
となります。

(3)表の小さい方から答えにたどり着くまで埋める
2行目を考えましょう。2行目は
『Cの2番目まででC[2]がxであるような数列の個数』
を表します。

A[2]~B[2]=2~6ですから、xが2~6以外の箇所は数列Cが作れません。つまり0が埋まります。

・x=2
dp[1][0]=0
dp[1][1]=1
dp[1][2]=1
であることがわかっています。
例えばdp[1][1]は『Cの1番目まででC[1]が1であるような数列の個数』を表しています。
であればdp[1][1]で作れるCの2番目に「2」をくっつけることで2番目までの数列を作れます。
dp[1][2]も同様に『Cの1番目まででC[1]が2であるような数列の個数』を表していますから、作られた数列Cの2番目に「2」をくっつけることで数列が作れます。
具体的には
dp[1][1]：C=(1)
dp[1][2]：C=(2)
となっているわけですから、それぞれに「2」をくっつけて
dp[2][2]：C=(1,2),(2,2)
とできるわけです。
ゆえにdp[2][2]=2であることがわかります。

・x=3
dp[1][0]=0
dp[1][1]=1
dp[1][2]=1
dp[1][3]=1
です。
x=2のときと同様に、dp[1][1]~dp[1][3]で作れるCの2番目に「3」をくっつければよいことがわかります。
具体的には
dp[1][1]：C=(1)
dp[1][2]：C=(2)
dp[1][3]：C=(3)
となっているわけですから、それぞれに「3」をくっつけて
dp[2][2]：C=(1,3),(2,3),(3,3)
とできるわけです。
ゆえにdp[2][3]=3であることがわかります。

・x=4～6
同じように考えれば
dp[2][4]=dp[1][0]~dp[1][4]の和
dp[2][5]=dp[1][0]~dp[1][5]の和
dp[2][6]=dp[1][0]~dp[1][6]の和
となります。
2行目を埋めると以下のようになります。

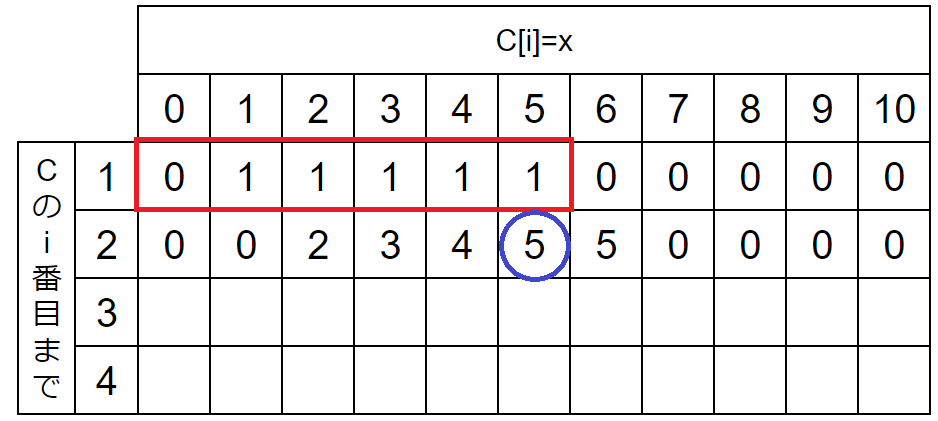
例えばdp[2][5](青丸部分)はdp[1][0]~dp[1][5](赤枠部分)の和であることがわかります。

一般には以下の式で計算できます。

A[i]≦x≦B[i]の場合
dp[i][x]=dp[i-1][0]~dp[i-1][x]の和

ここまでわかれば表は埋まるのですが、和を取る部分をそのままsum等で実装するとTLEします。
そのため累積和(Cumulative sum)を使います。累積和は数列のある箇所までの値を全て足したものです。
dpのi行目を埋める前にi-1行目の累積和を確認しておくわけです。

例えば次にi=3の行を埋める時は先にi=2の行について累積和を計算しておきます。
2行目：0 0 2 3 4 5 5 0 0 0 0

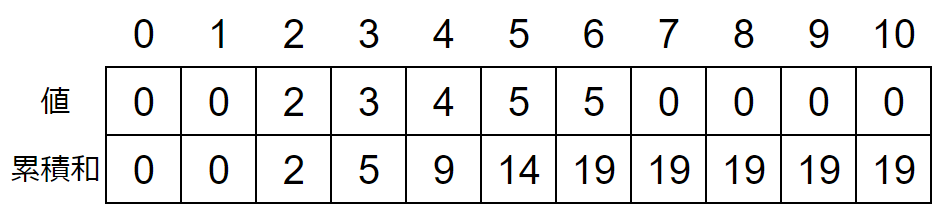
例えば4番目までの累積和=0+0+2+3+4=9となります。
i-1行目の累積和をcum_sumとして、以下の式で計算できます。
・cum_sum[0]=dp[i-1][0]
・cum_sum[k]=cum_sum[k-1]+dp[i-1][k]
k-1番目までの累積和がわかっていればそれにdp[i-1][k]を足すことでk番目までの累積和も計算できるというわけです。
4番目までの累積和で言えばcum_sum[4]=cum_sum[3]+dp[i-1][4]=5+4=9と計算できます。

事前に累積和を計算しておくことで(dp[i-1][0]~dp[i-1][x]の和)=cum_sum[x]と計算できます。

(4)答えを出力する
表をすべて埋めると以下のようになります。

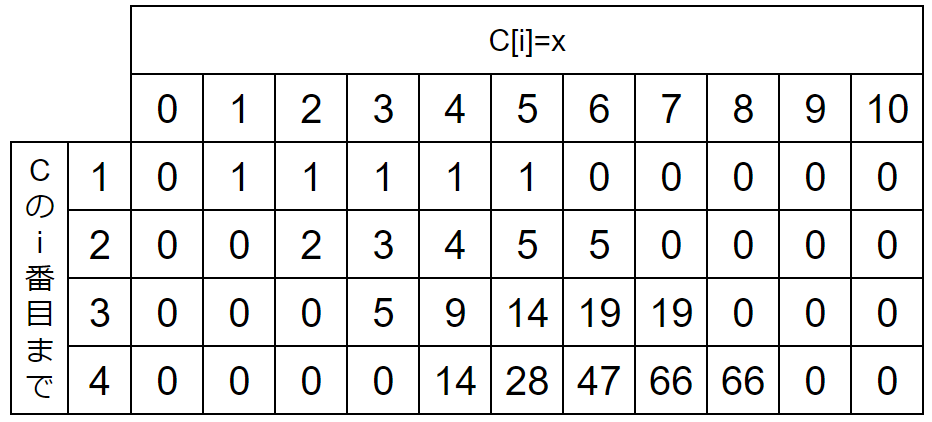
最後の行(i=4)は『Cの4番目まででC[4]がxであるような数列の個数』を表していますから、これらを全部足したものが答えです。
ゆえに最後の行の値をすべて足し、余りを取って出力すればOKです。

0+0+0+0+14+28+47+66+66+0+0=221
よって221が答えとなります。

pythonだとTLEするのでpypyで提出します。

【提出】

# pypyで提出

# 入力の受け取り
N=int(input())
# 0番を埋めるために[0]を先頭へ追加
A=[0]+list(map(int, input().split()))
B=[0]+list(map(int, input().split()))

# あまりの定義
mod=998244353

# 表の作成
# 『Cのi番目まででC[i]がxであるような数列の個数』
dp=[[0]*3001 for i in range(N+1)]

# x=A[i]~B[i]
for x in range(A[1],B[1]+1):
    # dp[1][x]に1を埋める
    dp[1][x]=1

# i=2~Nまで
for i in range(2,N+1):
    # 累積和
    # 累積和リストを作成
    cum_sum=[0]*(3001)
    # 0番目：cum_sum[0]=dp[i-1][0]
    cum_sum[0]=dp[i-1][0]
    # k=1~3000まで
    for k in range(1,3001):
        # 累積和の計算
        cum_sum[k]=cum_sum[k-1]+dp[i-1][k]
        # 余りを取る
        cum_sum[k]%=mod

    # x=0~3001まで
    for x in range(3001):
        # A[i]<=x<=B[i]ならば
        if A[i]<=x<=B[i]:
            # dp[i][x]=(dp[i-1][0]~dp[i-1][x]の和)=cum_sum[x]
            dp[i][x]=cum_sum[x]

# 表のN行目を全て足す
ans=sum(dp[N])
# 余りを取る
ans%=mod
# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】