強化学習を強化学習（ぬるっと復習）
なので、内容のムラと語尾がバラバラなのも気にしない
強化学習
機械学習の一種である。
・教師あり学習
・教師なし学習
・強化学習
教師あり学習は、行動一つ一つに正解が存在し、その正解を学習して行くが、
強化学習は、行動一つ一つに正解は与えられていないが、それら一連の行動によって得られる結果（正解）は得られる。
その結果から、各行動の価値を決定していく。
現在の状態(環境)を観測（取得）し、次に取るべき行動を決定する問題を扱う機械学習の分野。
枠組み
主に環境と学習行うエージェントが存在する。
環境とは、タスク・学習したい対象の状態であるとも言える。
エージェントには、現在の環境(状態)を評価し、行動を決定する。
また、環境はエージェントの行動により変化したり、報酬を与えたりする。
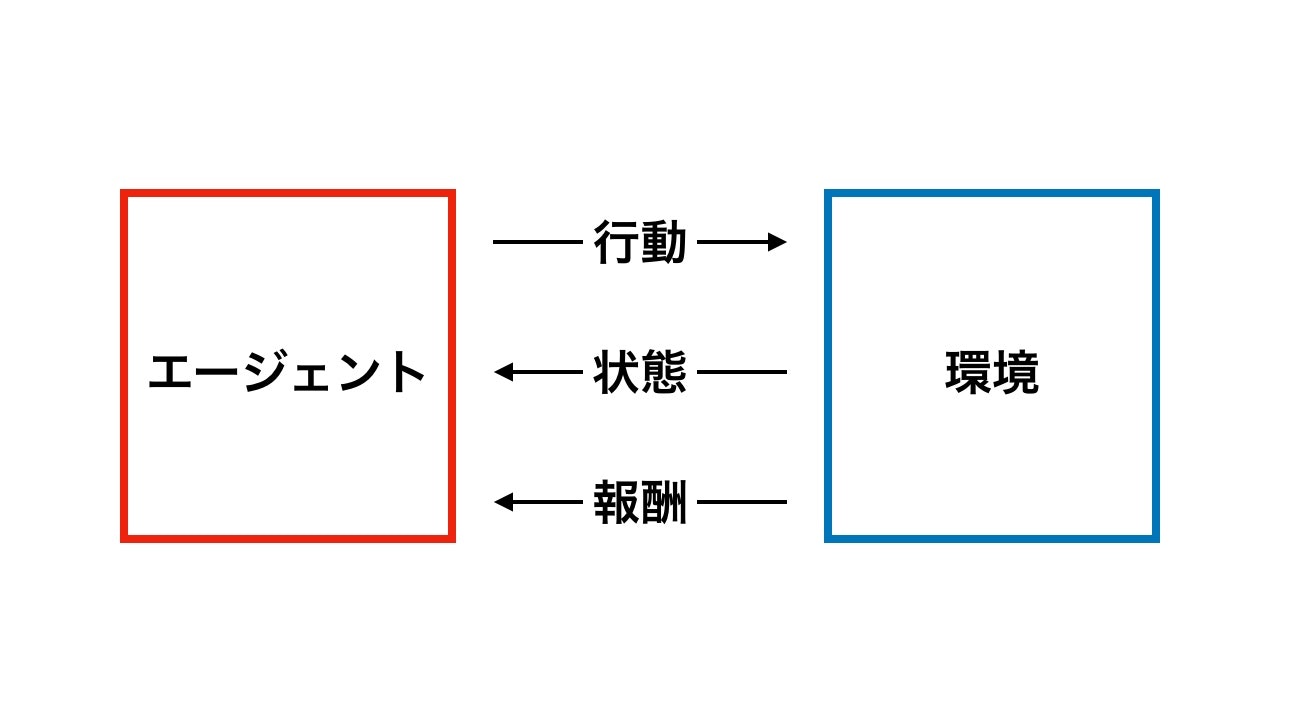
将棋だと、環境が現在の盤面であり、それをエージェントとなる棋士が読み取り、評価。
勝利するためには、どのような一手が良いのかを決定、環境となる盤面に反映させる。
そして、最終的には勝利した、負けたという報酬が得られ、以後の試合における行動決定に活かされるという流れ。
なお、この報酬とは即時報酬と呼ばれ、ゲームタスク等では、タスク(ゲーム)の終了時に報酬が得られる。
他の環境では、行動を行うごとに得られたりする。
強化学習の目的は、この即時報酬の合計（利得・累積報酬）を最大にするための、行動選択のポリシー（ルール）を学習することである。
現状
いろんなタスクに使われています(適当)
・セルラー中心システムの周波数帯の動的割り当て
・在庫管理・生産ラインの最適化とか
・ゲームのCPUとか
・AlphaGoとか
・Googleのサーバーセンターの消費電力最小化とか
あと、最近ではマーケティングにも利用されていて、個人的にはホット
理論
強化学習をモデル化する際に、以下の要素をベースに考えて行かないといけない
・State: $ s \in S $
環境の状態
・Model: $ T(s,a,s') $
状態sの時に行動aを行うことで状態がs'に変化するということを意味する。
・Action: $ a(s) \in A $
現在の状態sにおいて行う行動
・Reward:$r(s,a),r(s),r(s,a,s') $
状態sの状態で行動aや状態s'に変化したことにより得られる報酬を示す報酬関数
モデルは以下のように定義することができる。
M = (S,A,T,r)\\
状態遷移が確率的に起こる確率システムのモデルです。
マルコフ決定過程(Markov decision processes: MDP)
そして、状態遷移がマルコフ性を満たすため、このモデルはマルコフ決定過程モデルと呼びます。
マルコフ性とは、確率的に変化する過程において、次の状態への変化を表す条件付き確率分布Prが、現在状態のみに依存し、過去のいかなる状態にも依存しない特性を持つということを意味します。
本来の確率過程(確率的に変化する過程)は、次の確率分布に過去の行動や状態が、将来の状態に反映すると考えられます。
Pr(s_{t+1}=s',r_{t+1}=r | s_{t},a_t,r_t,s_{t-1},a_{t-1},...,r_1,s_0,a_0)\\
ここに過去の情報が影響しないというマルコフ性を仮定すると、次式のようになります。
Pr(s_{t+1}=s',r_{t+1}=r | s_{t},a_t)\\
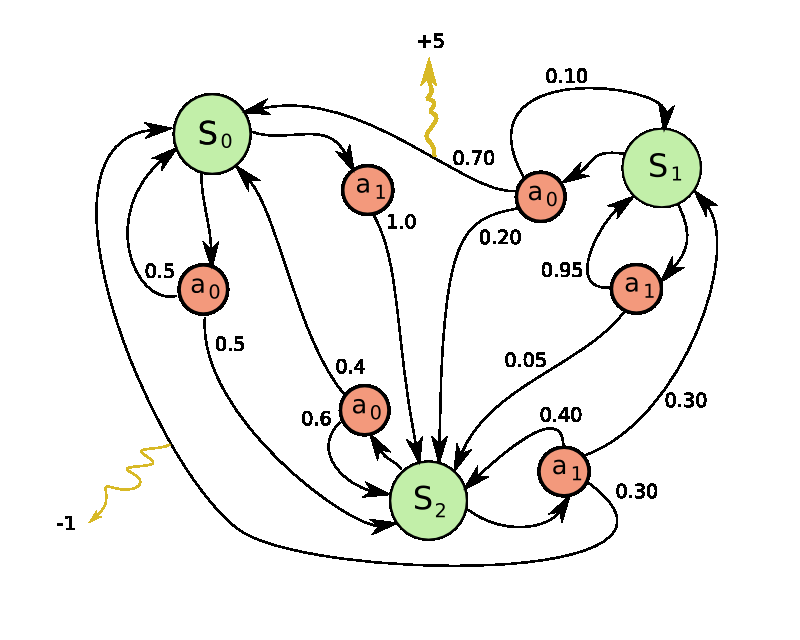[ 3つの状態と2つの行動をもつ簡単な MDP の例 ]
収益
行動を選択して行く際に、それぞれの行動を取ることで、今度どの程度の報酬が得られるのかは、すぐにはわからない。
この将来得られる期待される報酬の合計を収益と呼び、次のように泡らすことができる。
R_t = r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+ \cdots =\sum_{k=0}^\infty \gamma^kr_{t+k+1}\\
ここで、$ \gamma(0 \leq \gamma \leq 1) $は割引率であり、将来得られる報酬を現在値にどの程度影響させるのかを意味している。
$ \gamma=1 $の場合、将来得られる報酬を全て考慮することになり、 $ \gamma=0 $の場合、次の時刻で得られる報酬しか影響しないことになる
状態価値関数
このままでは収益は計算できない、状態遷移のモデルと方策がわかっている場合は、それに対応した収益を計算できるようになる
そのためには、現在の状態sと行動aの価値を考える必要がある。
現在の状態sにいることの価値を次のように表す。
V_s^{\pi} = E\{ R_t|s_t=s\}\\
これは、方策πにおいて現在の状態にいることで、今後得られる収益の期待値を意味する。
定義に従って、変形していく
\begin{split}
V_s^{\pi} &= E\{ R_t|s_t=s\} \\
&=E\{ r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+ \cdots|s_t=s\} \\
&=E\{ r_{t+1}+\gamma (r_{t+2}+\gamma^2 r_{t+3}+ \cdots)|s_t=s\} \\
&=E\{ r_{t+1}+|s_t=s\} \\
&=\sum_{a \in A(s)} \pi(s,a) \{
\sum_{s' \in S} P^a_{ss'} (R^a_{ss'}+\gamma E\{R_{t+1}|s_{t+1}=s'\})\} \\
&=\sum_{a \in A(s)} \pi(s,a) \{
\sum_{s' \in S} P^a_{ss'} (R^a_{ss'}+\gamma E\{R_{t+1}=s'\})\}\\
\end{split} \\
$ V^{\pi}_s $ 各要素間の関係を表す連立一次方程式にいなっている。
この式をBellman方程式と呼ぶ。
一般的には、動的計画法として知られる数学的最適化において、最適性の必要条件を表す方程式である。
行動価値関数
現在の状態で行動を取ることの価値を次のように表す。
Q_{s,a}^{\pi} = E\{ R_t|s_t=s,a_t=a\}\\
これは、方策πにおいて現在の状態で行動aを選択することで、今後得られる収益の期待値を意味する。
行動価値関数も状態価値関数と同様に、展開をすることで、Bellman方程式を得ることができる。
Q_{s,a}^{\pi} = \sum_{s \in S} \pi(s,a) \left \{
\sum_{a' \in A(s)} P^a_{ss'} (r^a_{ss'}+\gamma E\{R_{t+1}=s'\})\right \}\\
これらbellman方程式をとくことにより,行動選択のルールとなる最適な方策が得られる。
参考
http://sysplan.nams.kyushu-u.ac.jp/gen/edu/RL_intro.html
https://qiita.com/Hironsan/items/56f6c0b2f4cfd28dd906
https://qiita.com/icoxfog417/items/242439ecd1a477ece312
http://www.sist.ac.jp/~kanakubo/research/reinforcement_learning.html
http://sysplan.nams.kyushu-u.ac.jp/gen/edu/RL_intro.html
https://qiita.com/sugulu/items/3c7d6cbe600d455e853b
https://ja.wikipedia.org/wiki/Q%E5%AD%A6%E7%BF%92
https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%AB%E3%83%9E%E3%83%B3%E6%96%B9%E7%A8%8B%E5%BC%8F#%E5%8B%95%E7%9A%84%E6%B1%BA%E5%AE%9A%E5%95%8F%E9%A1%8C
http://d.hatena.ne.jp/masatoi/20060715/1152943285
http://yamaimo.hatenablog.jp/entry/2015/08/23/200000
http://yamaimo.hatenablog.jp/entry/2015/08/24/200000
http://yamaimo.hatenablog.jp/entry/2015/09/03/200000
http://yamaimo.hatenablog.jp/entry/2015/09/04/200000