はじめに
みなさん、強化学習してますか?
強化学習はロボットや、囲碁や将棋のようなゲーム、対話システム等に応用できる楽しい技術です。
強化学習とは、試行錯誤を通じて環境に適応する学習制御の枠組みです。教師あり学習では入力に対する正しい出力を与えて学習させました。強化学習では、入力に対する正しい出力を与える代わりに、一連の行動に対する良し悪しを評価する「報酬」というスカラーの評価値が与え、これを手がかりに学習を行います。以下に強化学習の枠組みを示します。
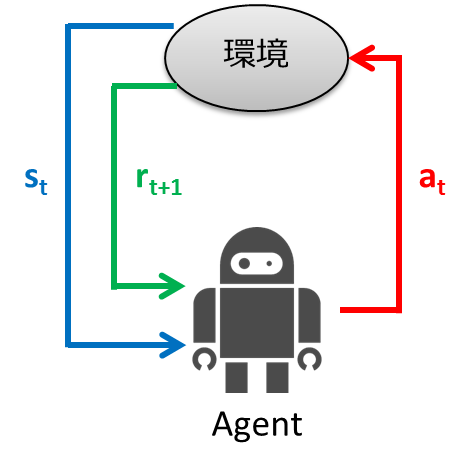
- エージェントは時刻 $t$ において環境の状態 $s_t$ を観測
- 観測した状態から行動 $a_t$ を決定
- エージェントは行動を実行
- 環境は新しい状態 $s_{t+1}$ に遷移
- 遷移に応じた報酬 $r_{t+1}$ を獲得
- 学習する
- ステップ1から繰り返す
強化学習の目的は、エージェントが取得する利得(累積報酬)を最大化するような、状態から行動へのマッピング(政策)を獲得することです。
強化学習では上記の枠組みをマルコフ決定過程(Markov decision processes: MDP)によってモデル化し、学習アルゴリズムを考えるといったことが行われます。本稿では、強化学習について理論編と実践編に分けて解説します。理論編では、MDPおよび学習アルゴリズムについて説明し、実践編ではプログラミング言語Pythonを用いて理論編で説明したことを実装していきます。順番に読むことをおすすめしますが、「こまけぇこたぁいいんだよ!」という方は理論編を飛ばして実践編を読んでください。
理論編
まず、強化学習の理論を例を交えて説明していきます。ここでは例題の問題設定を説明した後、マルコフ決定過程について説明します。マルコフ決定過程について理解できたところで、その学習方法について説明します。
問題設定
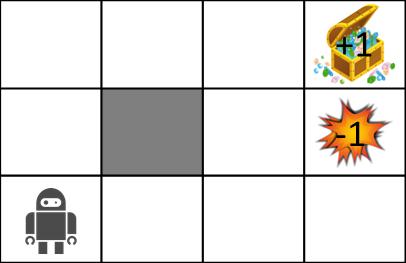
さて、MDPを説明するにあたって以下のような迷路の世界を考えてみましょう。
迷路の世界のルールは以下の通りです。
- エージェントはあるグリッドの中にいます
- エージェントは壁(灰色)を越えられません
- エージェントは自分が思った通りに動けるとは限りません
- 80%の確率で正しく動けますが、10%の確率で動こうと思っていた方向の左側へ動き、もう10%の確率で右側へ動きます
- 動こうと思った場所に壁があった場合は、その場にとどまります
- エージェントは各時刻に報酬を受け取ります
- ゴール(宝箱)やトラップ(爆発)にたどり着くとゲーム終了し、スタート位置に戻ります
確率的な遷移について以下の図を用いてもう少し詳しく説明します。
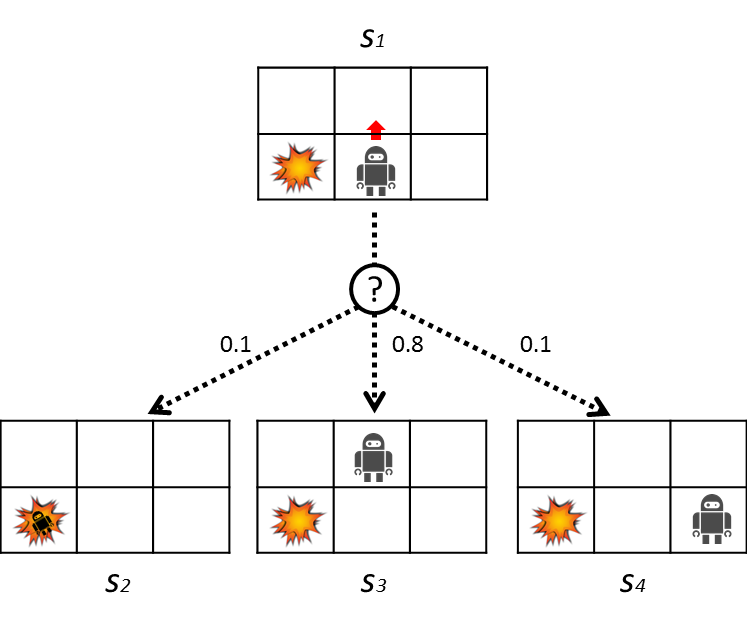
ここではロボットは上に動こうとしています。このとき80%の確率で上に動けますが、10%の確率で左側に動き、残りの10%の確率で右側に動いてしまいます。遷移確率は以下の表のようになります。
| $s'$ | $P(s' \mid s_1, a)$ |
|---|---|
| $s_2$ | 0.1 |
| $s_3$ | 0.8 |
| $s_4$ | 0.1 |
マルコフ決定過程(Markov decision processes: MDP)
さて、問題設定はわかったでしょうか?わかったところで、問題をMDPでモデル化します。
MDPは以下の4項組で定義されます
M = (S, A, T, R)
それぞれ何なのかというと、
- 状態集合: $s \in S$
- 行動集合: $a \in A$
- 遷移関数: $T(s, a, s') \sim P(s' \mid s, a)$
- 報酬関数: $R(s)$, $R(s, a)$, $R(s,a,s')$
それぞれ上で説明した問題設定に当てはめて考えてみます。
- 状態集合は環境がとりうる状態の集合を表しており、例題の場合はグリッドのすべてのセルを表しています。
- 行動集合はエージェントがとりうる行動の種類のことです。例題の場合、エージェントは上下左右に動くことができるので4種類です。
- 遷移関数とは、ある状態 $s$ で行動 $a$ を取った時に次の状態 $s'$ へどのくらいの確率で遷移するかということを表しています。上の図で説明した通りです。
- 報酬は観測した状態から取るべき行動を決定し、新たに遷移した結果として環境から受け取る値のことです。後で詳しく説明します。
このMDPの目的は利得(=累積報酬)を最大化する行動戦略を学習することです。この行動戦略のことを政策と呼びます。
政策についてもう少し詳しく
MDPでは最適な政策 $\pi^*: S \rightarrow A$ を得ることが目的です。政策は状態から行動へのマッピングを行う関数とみなせます。
政策は各状態で取るべき行動を教えてくれます。また、最適な政策は期待利得を最大化します。
遷移した時に得られる報酬を変化させたときの最適な政策の変化を見てみましょう。
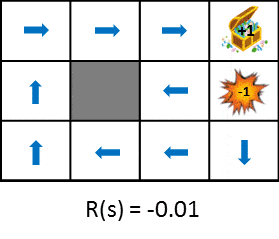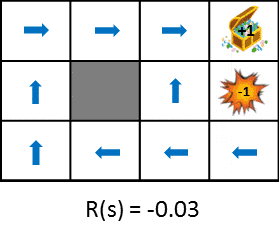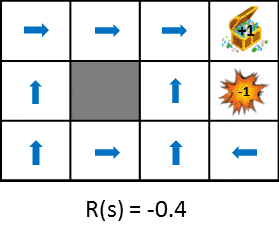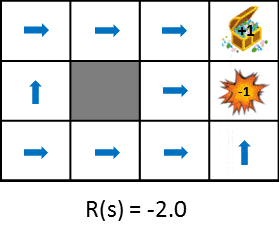
この図では状態遷移で得られる報酬をだんだん小さく(ペナルティを大きく)した時における政策の変化を示しています。政策は得られる期待利得を最大化するという考え方から学習します。そのため、状態遷移によるペナルティが小さければ遠回りしてでもゴールを目指そうとし、ペナルティが大きければ速やかにゲームを終了させる戦略を取るようになります。比較しやすいように静止画も用意しました。
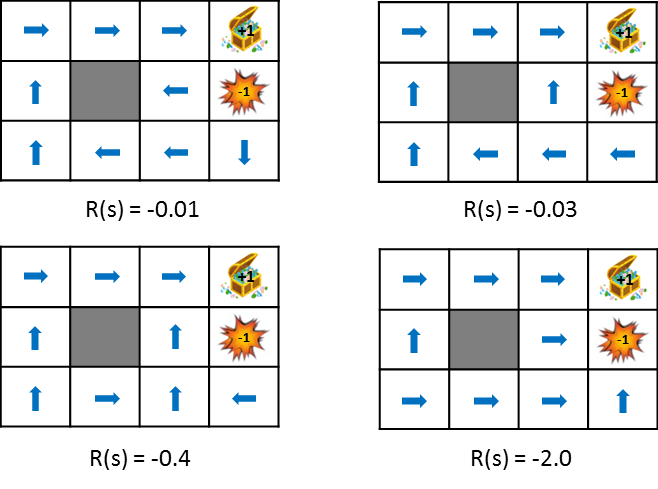
報酬についてもう少し詳しく
さて、ここまでで政策を学習するためには累積報酬を最大化すると述べました。
各時刻に報酬 $R(s_t)$ を得ることができるので、累積報酬は以下のように表せます。
\begin{align}
U([s_0, s_1, s_2,\ldots]) &= R(s_0) + R(s_1) + R(s_2) + \cdots \\
&= \sum_{t=0}^{\infty}R(s_t)
\end{align}
このように単純な累積報酬を使ってもいいのですが、いくつかの理由から以下の式のように将来得られる報酬を割引係数 $\gamma (0 \leq \gamma < 1)$ で割り引いた累積報酬が使われます。こうすることで、将来得られる報酬より現在得られる報酬を重視するようになります。
\begin{align}
U([s_0, s_1, s_2,\ldots]) &= R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots \\
&= \sum_{t=0}^{\infty}\gamma^t R(s_t)
\end{align}
このような割引報酬を使う理由としては以下があげられます。
- 計算的に値が発散しない
- 実際の環境では、時間がたつと環境が変化する可能性があるため、時系列のすべての報酬を同じ重みで考慮するのは妥当ではない
最適な政策の見つけ方
ここまででMDPというモデルについてはわかりました。残された問題はどうやって最適な政策を見つけるかということです。以下では最適な政策を見つけるアルゴリズムとして、価値反復法とQ-Learningについて説明します。
価値反復法(Value Iteration)
価値反復法では、状態 $s$ から最適な行動をとり続けた時の期待利得を計算します。得られる利得の期待値を考えるのは確率的な遷移が行われるためです。
この期待利得がわかれば、現在の状態 $s$ から将来にわたって得られる価値がわかるので、その価値を最大化するような行動を選択できるようにすればいいはずです。価値は以下の状態価値関数で求められます。複雑に見えますが、要するに(期待)割引累積報酬を計算しているだけです。
U(s) = R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')
この式の中にはmaxという非線形計算があり行列等で解くことは困難です。そのため反復的に計算を行って価値を徐々に更新していきます。これが価値反復法の名前の所以です。以下に価値反復法のアルゴリズムを示します。計算量は$O(|S|^2 |A|)$です。
1.すべての状態 $s$ について $U(s)$ を適当な値(ゼロなど)に初期化
2.すべての $U(s)$ について以下の式を計算して値を更新
U(s) \leftarrow R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')
>3.ステップ2を値が収束するまで繰り返す
上記の式にはmax計算をする部分がありますが、その値が最大値となる行動aを記録しておく必要があります。そのため $U(s)$ だけでは最適な政策(行動)がわかりにくいという問題があります。そこで以下のQ関数を導入します。行動価値関数とも呼ばれます。
```math
Q^*(s,a) = R(s) + \gamma \sum_{s'} P(s' \mid s,a) \max_{a'}Q^*(s', a')
**$Q^(s,a)$**は、状態$s$で行動aを選択後はずっと最適な政策を取り続ける場合の割引累積報酬の期待値を表しています。
$U(s)$ と $Q^(s,a)$ には、各状態における最大の値だけ保持するのか、それとも各行動に対して値を保持するのかの違いがあります。したがって、状態sにおける最大のQ値は $U(s)$ に等しくなり、このQ値を持つ行動aが最適な行動となります。以下の図がそのイメージです。
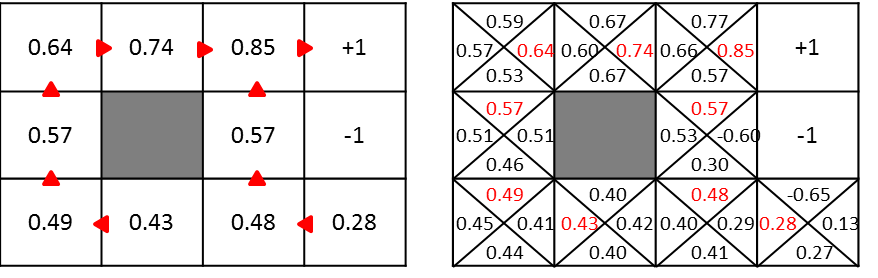
Q関数を用いた場合の価値反復法は以下のようになります。
1.すべての状態 $s$ について $Q^*(s,a)$ を適当な値(ゼロなど)に初期化
2.すべての $Q^*(s,a)$ について以下の式を計算して値を更新
Q^(s,a) \leftarrow R(s) + \gamma \sum_{s'} P(s' \mid s,a) \max_{a'}Q^(s', a')
>3.ステップ2を値が収束するまで繰り返す
ここまでくれば最適な政策$\pi ^*(s)$を見つけるのは簡単です。以下で求められます。
```math
\pi^*(s) = arg\max_{a}Q^*(s,a)
計算例
せっかくなので試しに以下の赤い場所の価値を計算してみましょう。
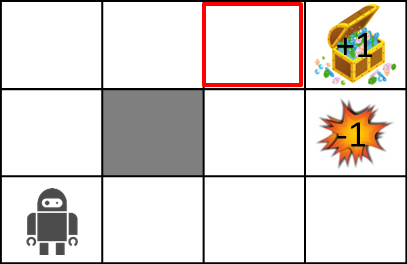
計算には以下の式を使います。
U(s) \leftarrow R(s) + \gamma \max_a\sum_{s'} P(s' \mid s,a) U(s')
$\gamma = 0.5$、 $R(s) = -0.04$、遷移確率は進みたい方向に0.8、その左右に0.1ずつとします。
以上の条件のとき、赤い場所の値は・・・
\begin{align}
U(s) &= -0.04 + 0.5 \cdot (0.8 \cdot 1 + 0.1 \cdot 0 + 0.1 \cdot 0)\\
&= -0.04 + 0.4\\
&= 0.36
\end{align}
と求められます。
Q-Learning
さて、価値反復法で最適な政策が求められて一安心。そうは問屋がおろしません。何が問題なのでしょうか?
今までは状態遷移確率についてわかっていました。しかし現実の問題を考えると状態遷移確率がわかっていることは珍しいです。チェスや将棋を思い浮かべてみてください。ある盤面(状態)から別の盤面(別の状態)へ遷移する確率はあらかじめ与えられているでしょうか?与えられていませんよね?そのような場合は価値反復法は使えません。
そこで出てくるのが価値反復法の強化学習版ともいえるQ-Learningです。Q-Learningでは
$\hat{Q}^{*}(s,a)$の推定値$\hat{Q}^{*}(s_t, a_t)$を計算します。Q-Learningを使うことで、遷移確率がわからない状況でも最適な政策の学習を行うことができます。Q-Learningのアルゴリズムは以下の通りです。
1.適当な値で $\hat Q^*(s_t, a_t)$ を初期化
2.以下の式を用いて行動価値の推定値を更新。ただし $\alpha$ は学習率で $0 \leq \alpha \leq 1$。
\hat Q^(s_t, a_t) \leftarrow \hat Q^(s_t, a_t) + \alpha \Bigl[ r_{t+1} + \gamma \max_{a \in A}\hat Q^(s_{t+1}, a) - \hat Q^(s_t, a_t) \Bigr]
>3.時間ステップ $t$ を $t+1$ へ進めて2へ戻る
この計算を繰り返すことで最適な $Q^*(s,a)$ を得ることができます。
<!--
実際に価値反復法の更新式(Q関数版)とQ-Learningの更新式を比べてみると、価値反復法ではQ関数の計算に遷移確率 $P(s' \mid s,a)$を用いているのに対し、Q-Learningを使う状況では未知なので使用していない。繰り返し計算を行うことで
-->
# 実践編
上で説明したことをPythonでやったらどうなるかについて見ていきましょう。
## 価値反復法
まずは価値反復法からです。
価値反復法は[UC Berkeley](https://github.com/aimacode/aima-python)のコード(mdp.py)がきれいだったので、それを基に説明します。
### MDPクラス
まずは基底クラスとなるMDPから。これを継承してGridMDPクラスを作ります。
```py3
class MDP:
def __init__(self, init, actlist, terminals, gamma=.9):
self.init = init
self.actlist = actlist
self.terminals = terminals
if not (0 <= gamma < 1):
raise ValueError("An MDP must have 0 <= gamma < 1")
self.gamma = gamma
self.states = set()
self.reward = {}
def R(self, state):
return self.reward[state]
def T(self, state, action):
raise NotImplementedError
def actions(self, state):
if state in self.terminals:
return [None]
else:
return self.actlist
__init__メソッドでは以下のパラメータを受け取ります:
- init: 初期状態.
- actlist: 各状態でとれる行動.
- terminals: 終了状態のリスト
- gamma: 割引係数
Rメソッドは各状態での報酬を返します。
Tメソッドは遷移モデルです。ここでは抽象メソッドとなっていますが、状態 $s$ で行動 $a$ を取った時に、次状態への遷移確率と次状態のタプル(probability, s')のリストを返します。GridMDPで実装していきます。
actionsメソッドは各状態でとれる行動のリストを返します。
GridMDPクラス
GridMDPクラスは基底クラスMDPの具象クラスです。例題で説明した迷路の世界を表現するためのクラスです。
class GridMDP(MDP):
def __init__(self, grid, terminals, init=(0, 0), gamma=.9):
grid.reverse() # because we want row 0 on bottom, not on top
MDP.__init__(self, init, actlist=orientations,
terminals=terminals, gamma=gamma)
self.grid = grid
self.rows = len(grid)
self.cols = len(grid[0])
for x in range(self.cols):
for y in range(self.rows):
self.reward[x, y] = grid[y][x]
if grid[y][x] is not None:
self.states.add((x, y))
def T(self, state, action):
if action is None:
return [(0.0, state)]
else:
return [(0.8, self.go(state, action)),
(0.1, self.go(state, turn_right(action))),
(0.1, self.go(state, turn_left(action)))]
def go(self, state, direction):
state1 = vector_add(state, direction)
return state1 if state1 in self.states else state
def to_grid(self, mapping):
return list(reversed([[mapping.get((x, y), None)
for x in range(self.cols)]
for y in range(self.rows)]))
def to_arrows(self, policy):
chars = {(1, 0): '>', (0, 1): '^', (-1, 0): '<', (0, -1): 'v', None: '.'}
return self.to_grid({s: chars[a] for (s, a) in policy.items()})
__init__メソッドが受け取る引数はほぼMDPクラスと同じですが、grid引数を受け取る点が違います。gridには各状態での報酬が格納されています。以下のような感じで渡します。Noneは壁を表しています。
GridMDP([[-0.04, -0.04, -0.04, +1],
[-0.04, None, -0.04, -1],
[-0.04, -0.04, -0.04, -0.04]],
terminals=[(3, 2), (3, 1)])
goメソッドは指定した方向に移動した場合の状態を返します。
TメソッドはMDPで説明したとおりです。ここでは実際に実装されています。
to_gridやto_arrows メソッドは表示用のメソッドです。
価値反復法の実装
def value_iteration(mdp, epsilon=0.001):
U1 = {s: 0 for s in mdp.states}
R, T, gamma = mdp.R, mdp.T, mdp.gamma
while True:
U = U1.copy()
delta = 0
for s in mdp.states:
U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
for a in mdp.actions(s)])
delta = max(delta, abs(U1[s] - U[s]))
if delta < epsilon * (1 - gamma) / gamma:
return U
def best_policy(mdp, U):
pi = {}
for s in mdp.states:
pi[s] = argmax(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
return pi
def expected_utility(a, s, U, mdp):
return sum([p * U[s1] for (p, s1) in mdp.T(s, a)])
value_iteration関数は入力としてGridMDPのインスタンスと小さな値epsilonを受け取り、出力として各状態におけるU(s)を返します。以下のような感じです。
>> value_iteration(sequential_decision_environment)
{(0, 0): 0.2962883154554812,
(0, 1): 0.3984432178350045,
(0, 2): 0.5093943765842497,
(1, 0): 0.25386699846479516,
(1, 2): 0.649585681261095,
(2, 0): 0.3447542300124158,
(2, 1): 0.48644001739269643,
(2, 2): 0.7953620878466678,
(3, 0): 0.12987274656746342,
(3, 1): -1.0,
(3, 2): 1.0}
そして、value_iteration関数で計算した結果をbest_policy関数に渡してあげることで、最適な政策を求めます。
実行
以下が試すためのコードです。ただし、このままでは必要なモジュールをいくつかimportしていないので動きません。そのため実際に動かしたい場合はここのリポジトリをクローンして動かしてください。
sequential_decision_environment = GridMDP([[-0.04, -0.04, -0.04, +1],
[-0.04, None, -0.04, -1],
[-0.04, -0.04, -0.04, -0.04]],
terminals=[(3, 2), (3, 1)])
pi = best_policy(sequential_decision_environment, value_iteration(sequential_decision_environment, .01))
print_table(sequential_decision_environment.to_arrows(pi))
実行結果として、以下の政策を得られます。
> > > .
^ None ^ .
^ > ^ <
Q-Learning
へんじがない、ただのしかばねのようだ
Q-Learningは体力のある時に書かせてください。
参考資料
Udacityの講義動画。文字は読みにくいが、話は分かりやすい。
日本語の資料
英語の資料
- Reinforcement Learning: A User’s Guide
- Introduction to Reinforcement Learning
- Introduction Reinforcement Learning
Value Iterationに関して図を交えてわかりやすく解説している資料
- Markov Decision Processes and Exact Solution Methods:
- Markov Decision Processes Value Iteration
- Markov Decision Processes
Value Iteration実装するときに参考になる資料
- Artificial Intelligence: Markov Decision Process
- Artificial Intelligence: A Modern Approach
- Value Iteration
- Pythonic Markov Decision Process (MDP)
価値関数の数式展開が丁寧