はじめに
天体画像を複数の時期に観測すると、構造の位置や形が少しずつ変化していることがあります。超新星残骸の膨張やジェットの進展などがその典型例です。こうした変化を定量化するのが 固有運動解析 です。
本記事ではその中でも、二次元的な自由度をもつ固有運動の推定 を取り上げます。
特に X 線観測では画像がフォトンの「カウント数」として記録されるため、ガウス雑音よりも ポアソン統計を前提とするのが自然です。ここでは ポアソン尤度(C-statistic)に基づく最尤推定 を導入し、シミュレーションを通じてその仕組みを確認します。
このテーマは、修士課程から約3年間取り組んできた研究をまとめ直したものです。まだまだ浅いところもあると思いますが、何か参考になれば嬉しいです。
実装コード
本記事の実装コードは Google Colab こちら からご確認いただけます。
ポアソン尤度に基づく固有運動推定
画像同士をポアソン分布として比較
ここで扱うのは、2つの異なる時期に観測された画像です。仮に、ある時刻の画像を $\Lambda$、別の時刻の画像を $K$ としましょう。
1つの画素だけではカウントの違いが小さく、動きを判定するのは難しいです。そこで、ある範囲(領域 $\Omega$)をまとめて評価し、模様全体から位置の変化を統計的に推定します(詳細は 窓サイズはどう決めるか? を参照)。
各ピクセルのカウントはポアソン分布で表せます。これを領域内のピクセル全体で掛け合わせると、尤度は次の式になります。
\mathcal{L}
= \prod_{(x,y)\in\Omega}
\frac{e^{-\Lambda_{x,y}} \,\Lambda_{x,y}^{K_{x,y}}}{K_{x,y}!}
ただし、尤度は積の形なので値が非常に小さくなり、計算上扱いにくくなります。そこで対数を取って、対数尤度に書き換えます。
\ln \mathcal{L}
= \sum_{(x,y)\in\Omega}
\Big[ K_{x,y}\,\ln \Lambda_{x,y} - \Lambda_{x,y} - \ln(K_{x,y}!) \Big]
移動量を加えたモデルの構築
ここで求めたい量は 2 枚の画像間の平行移動(シフト) です。考え方はシンプルで、観測画像 $K$ はそのまま固定し、基準画像(モデル) $\Lambda$ をシフトさせながら、各シフト量がどれだけ観測を「尤もらしく」説明できるかをポアソン尤度で評価します。
観測は固定、モデルを動かす
以降は前提として、観測 $K$ を固定し、モデル $\Lambda$ を動かします。これは尤度の意味づけ(「観測カウントは固定された試行の結果、モデルはその期待値」)にも合致し、実装上も自然です。
厳密にはモデル固定、観測を動かしても良いが...
厳密には観測を動かすように統計的に定式化することも可能です。ポアソン分布の枠組みが崩れない限り、いずれの定式化でも「もっともらしいシフト位置」を尤度に基づいて決めることはできます。ただし観測を動かす場合には $K_{x,y}!$ の階乗がシフト依存になり、実装が煩雑になります。そのため、本記事ではモデル側を動かす形を採用しています。
シフトを $(x',y') = (x+\Delta_x, y+\Delta_y)$ とおくと、対数尤度は
\ln \mathcal{L}(\Delta_x,\Delta_y)
= \sum_{(x,y)\in\Omega}
\Big[ K_{x,y}\,\ln \Lambda_{x',y'} - \Lambda_{x',y'} - \ln(K_{x,y}!) \Big]
ここで $\ln(K_{x,y}!)$ はシフト $(\Delta_x,\Delta_y)$ に依存しない定数なので、最適化には影響しません。したがって実装では定数項を落とし、
\ln \mathcal{L}(\Delta_x,\Delta_y)
= \sum_{(x,y)\in\Omega}
\Big[ K_{x,y}\,\ln \Lambda_{x',y'} - \Lambda_{x',y'} \Big]
を最大化すれば最適化の上で同値です。
この考え方を整理したものが、ポアソン分布を用いたX線解析で広く用いられる C-statistic(Cash 1979)であり、次のように定義されます。
C(\Delta_x,\Delta_y)
= -2 \sum_{(x,y)\in\Omega}
\left[ K_{x,y}\,\ln \Lambda_{x',y'} - \Lambda_{x',y'} \right]
これは「対数尤度から定数項を落とし、符号を反転して 2 倍したもの」であり、$C$ を最小化することが対数尤度の最大化と等価になります。
最適化の対象と処理イメージ
ここまでで「移動量 $(\Delta_x, \Delta_y)$ を変化させながら $C$ を最小化する」と書きましたが、実際の処理イメージが分かりにくいと思います。そこで、もう少し直感的に説明します。
領域 Ω とは?
数式では $\Omega$ と書きましたが、これは「評価を行う画素の集合」を意味します。
実際の実装では、画像全体を使うのではなく、ある程度の大きさの 局所的な窓(window) を切り出して、その範囲で観測とモデルを比較します。
例えば半径10ピクセルの円形の窓を選んだ場合、$\Omega$ はその円の中の画素すべてを指します。窓を画像上のいろいろな場所に配置することで、場所ごとの固有運動を推定できるわけです。
モデルを「動かす」とは?
$(\Delta_x, \Delta_y)$ は「モデル画像をどのくらい動かすか」を表します。実装では整数ピクセル単位でずらすのが一般的です。たとえば $(\Delta_x, \Delta_y) = (1, -2)$ なら「右に1ピクセル、下に2ピクセル」動かすことを意味します。
(ちなみに、サブピクセル単位でモデルを動かす方法もあり、Vink et al. (2022) などで実際に用いられています。)
探索範囲は半径 $R$ の円とし、全ての候補を試して最も $C$ が小さくなるシフトを探します。数式で書くと、
(\hat{\Delta}_x, \hat{\Delta}_y)
= \arg\min_{\Delta_x^2 + \Delta_y^2 \leq R^2} C(\Delta_x, \Delta_y)
となります。ここで $R$ は探索半径です。
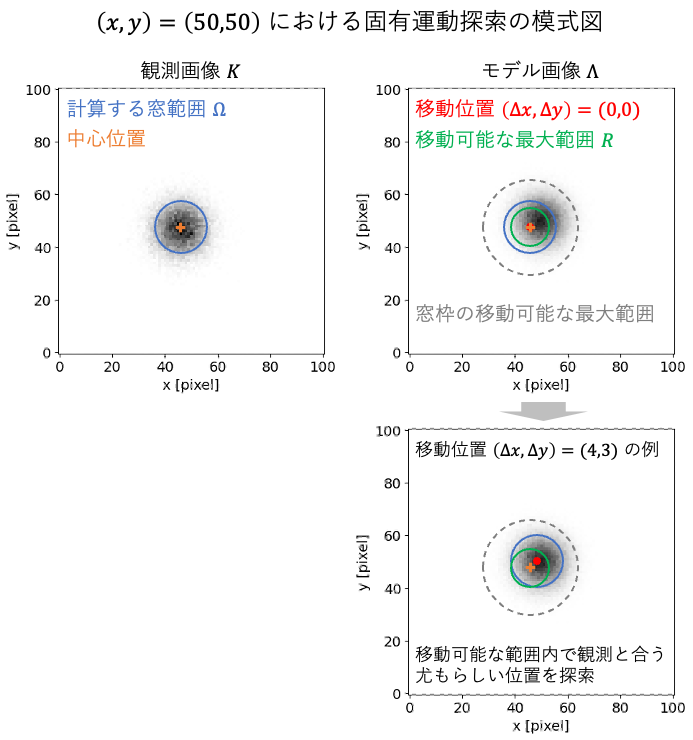
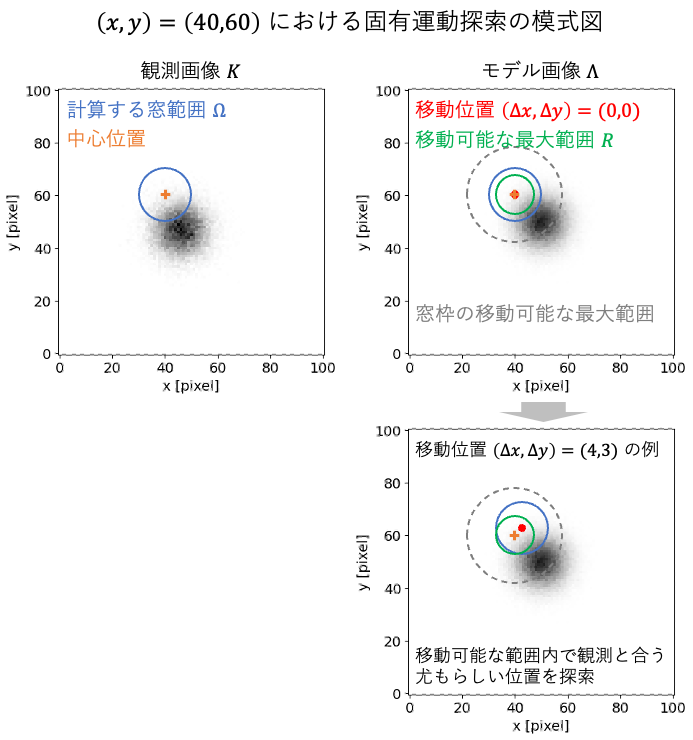
模式図でみる処理の流れ
文章だけではイメージが湧きにくいと思うので、下図で用語やパラメータの関係を図示します。
- 左上:評価に使う窓(青い円)が $\Omega$、その中心(オレンジの十字)が「基準位置」です。ここで観測とモデルを比較します。
- 右上:窓の中心を $(\Delta_x,\Delta_y)=(0,0)$ に置いた場合です。緑の円は「移動可能な最大範囲」$R$ を示し、灰色の破線はそのとき窓枠が取りうる最大範囲を表しています。探索はこの範囲内で行われます。
- 下:例として $(\Delta_x,\Delta_y)=(4,3)$ にシフトした場合です。窓全体をその分だけ動かし、観測と最もよく一致する「尤もらしい位置」を探します。
今回の対象は構造がはっきりしているため、中心付近の固有運動は精度よく推定できます。
構造の端ではカウント数が減少し、特徴がノイズに埋もれるため推定精度は低下します。
このように固有運動解析は、同じ構造を見ていても「どの位置を基準に推定するか」に強く依存します。理想的には構造の中心で推定するのが望ましいですが、実務ではその位置を一意に決めるのが難しい場合もあり、全体を通して推定することもあります。次節では、シミュレーションを通じてその影響を詳しく見ていきます。
シミュレーション実装例
ここでは人工的に作った画像を用いて、手法の動作を確認してみます。
まずはシンプルに ガウス分布ひとつ を使った例から始め、その後で カウント不足のケース や 複数構造を含むケース も確認します。
以下は、ポアソン尤度による固有運動推定の実装例です。
詳細な実装(全関数定義やシミュレーション例)は Google Colab にまとめています。
実装コードの一部(基本例:固有運動推定と誤差推定)
import numpy as np
import cv2
from tqdm import tqdm
from scipy.signal import convolve
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import colormaps
from matplotlib import lines as mlines
from matplotlib.colors import LinearSegmentedColormap, ListedColormap
# DS9 カラーマップの実装記事:https://qiita.com/sakaimaging/items/b30ca36be1c43beecde5
ds9_b_cdict = {
'red': [(0.0, 0.0, 0.0), (.25, 0.0, 0.0), (.5, 1.0, 1.0), (1.0, 1.0, 1.0)],
'green': [(0.0, 0.0, 0.0), (.5, 0.0, 0.0), (.75, 1.0, 1.0), (1.0, 1.0, 1.0)],
'blue': [(0.0, 0.0, 0.0), (.25, 1.0, 1.0), (.5, 0.0, 0.0), (.75, 0.0, 0.0), (1.0, 1.0, 1.0)]
}
ds9_b_cmap = LinearSegmentedColormap('ds9_b', ds9_b_cdict)
colormaps.register(name='ds9_b', cmap=ds9_b_cmap, force=True)
ds9_b_r_cmap = ds9_b_cmap.reversed()
colormaps.register(name='ds9_b_r', cmap=ds9_b_r_cmap, force=True)
def make_circular_window(window_radius):
"""
円形ウィンドウを作成する。
パラメータ
----------
window_radius : int
円の半径(ピクセル単位)。
戻り値
-------
window : ndarray of shape (2*window_radius+1, 2*window_radius+1)
半径以内を 1、それ以外を 0 とする二値マスク配列。
"""
size = 2*window_radius + 1
window = np.zeros((size, size))
center = window_radius
for y in range(size):
for x in range(size):
if np.sqrt((x-center)**2 + (y-center)**2) <= window_radius:
window[y, x] = 1
return window
def c_stat(obs_counts, model_counts, eps=1e-3):
"""
C統計量(Cash statistic)を各ピクセルで計算する。
パラメータ
----------
obs_counts : ndarray
観測カウント画像(ポアソン分布に従う)。
model_counts : ndarray
モデルカウント画像(観測の露出に正規化されたもの)。
eps : float, optional (default=1e-3)
0除算を避けるための小さな値。
戻り値
-------
cstat : ndarray
各ピクセルごとのC統計量。
"""
safe_model = np.clip(model_counts, eps, None) # ゼロを回避
cstat = -2 * (obs_counts * np.log(safe_model) - safe_model)
return cstat
def make_search_shift_list(search_radius):
"""
円形の探索半径内に含まれるシフト候補 (dy, dx) を生成する。
パラメータ
----------
search_radius : int
探索する最大半径(ピクセル単位)。
例: search_radius=3 → -3〜+3 の範囲を探索。
戻り値
-------
search_list : list of [dy, dx]
円領域内に含まれるシフト候補のリスト。
"""
search_list = []
for dy in range(-search_radius, search_radius+1):
for dx in range(-search_radius, search_radius+1):
if np.sqrt(dx**2 + dy**2) <= search_radius:
search_list.append([dy, dx])
return search_list
def _max_shift_radius(search_list):
"""
シフト候補リストから最大の絶対シフト量を求める。
パラメータ
----------
search_list : list of [dy, dx]
シフト候補のリスト。
戻り値
-------
r : int
シフト量の最大値。
"""
return max(max(abs(dy), abs(dx)) for dy, dx in search_list)
def estimate_proper_motion(obs_counts, model_counts,
window_radius=30, search_radius=15,
use_tqdm=True, return_cstat_map=False):
"""
C統計量の最小化に基づいて、二次元的な固有運動(シフト量)を推定する。
パラメータ
----------
obs_counts : ndarray of shape (H, W)
観測カウント画像(ポアソン分布に従う)。
model_counts : ndarray of shape (H, W)
モデルカウント画像(観測の露出に正規化されたもの)。
window_radius : int, optional (default=30)
C統計量マップを平滑化する円形ウィンドウの半径。
search_radius : int, optional (default=15)
シフト候補を探索する最大半径(ピクセル単位)。
use_tqdm : bool, optional (default=True)
True の場合、シフト探索中に tqdm による進捗バーを表示する。
return_cstat_map : bool, optional (default=False)
True の場合、全シフト候補に対するC統計量マップ (cstat_cube) も返す。
戻り値
-------
flow : ndarray of shape (H, W, 2)
各ピクセルにおける推定シフトベクトル (dy, dx)。
search_list : list of [dy, dx], optional
return_cstat_map=True の場合のみ返す。
cstat_cube : ndarray of shape (N_shifts, H, W), optional
return_cstat_map=True の場合のみ返す。
"""
search_list = make_search_shift_list(search_radius)
window = make_circular_window(window_radius)
H, W = obs_counts.shape
r = _max_shift_radius(search_list)
best_cstat = np.full((H, W), np.inf, dtype=float)
flow = np.zeros((H, W, 2), dtype=float)
pad_model = np.pad(model_counts, ((r, r), (r, r)),
mode='constant', constant_values=1e-3)
cy, cx = pad_model.shape[0] // 2, pad_model.shape[1] // 2
if return_cstat_map:
cstat_cube = []
iterator = tqdm(search_list, desc="Searching shifts", leave=False) if use_tqdm else search_list
for (dy, dx) in iterator:
y0 = cy - H//2 + dy
x0 = cx - W//2 + dx
shifted = pad_model[y0:y0+H, x0:x0+W]
cstat = c_stat(obs_counts, shifted)
cstat_smooth = convolve(cstat, window, mode='same')
if return_cstat_map:
cstat_cube.append(cstat_smooth)
mask = cstat_smooth < best_cstat
best_cstat[mask] = cstat_smooth[mask]
flow[mask] = (dy, dx)
if return_cstat_map:
return flow, search_list, np.array(cstat_cube)
else:
return flow
def plot_delta_c_map(search_list, cstat_cube, x0, y0):
"""
特定の座標 (x0, y0) における ΔC マップを可視化し、
68%, 90%, 95% 信頼区間と最小値の位置を表示する。
"""
# 注目ピクセルの C統計量
cstat_vals = cstat_cube[:, y0, x0] # yが行, xが列
cstat_min = np.min(cstat_vals)
delta_c = cstat_vals - cstat_min
# search_list を (dx, dy) に分解
dx_list = np.array([dx for dy, dx in search_list])
dy_list = np.array([dy for dy, dx in search_list])
# 最小点を特定
min_idx = np.argmin(cstat_vals)
best_dx, best_dy = dx_list[min_idx], dy_list[min_idx]
# グリッド化
dxu = np.unique(dx_list)
dyu = np.unique(dy_list)
grid = np.full((len(dyu), len(dxu)), np.nan)
for val, dx, dy in zip(delta_c, dx_list, dy_list):
ix = np.where(dxu == dx)[0][0]
iy = np.where(dyu == dy)[0][0]
grid[iy, ix] = val
# 可視化
plt.figure(figsize=(6,5))
im = plt.imshow(grid, origin="lower", cmap="gray",
extent=(dxu.min()-0.5, dxu.max()+0.5,
dyu.min()-0.5, dyu.max()+0.5))
plt.colorbar(im, label="ΔC")
# 信頼区間を等高線で描画
levels = [2.3, 4.61, 5.99]
labels = ["68% (ΔC=2.3)", "90% (ΔC=4.61)", "95% (ΔC=5.99)"]
colors = ["red", "orange", "blue"]
for lev, col in zip(levels, colors):
plt.contour(dxu, dyu, grid, levels=[lev], colors=[col])
# 最小点をマーカーで表示
plt.scatter(best_dx, best_dy, c="yellow", marker="x", s=50, label="Best-fit")
# 凡例用ハンドル
handles = [mlines.Line2D([], [], color=col, label=lab)
for lab, col in zip(labels, colors)]
handles.append(mlines.Line2D([], [], color="yellow", marker="x", linestyle="None",
label=f"Best-fit (dx,dy)=({best_dx},{best_dy})"))
plt.xlabel("dx [pixel]")
plt.ylabel("dy [pixel]")
plt.title(f"ΔC map at pixel (x,y)=({x0},{y0}), Cmin={cstat_min:.1f}")
plt.legend(handles=handles, fontsize="small")
plt.show()
def gaussian_2d(X, Y, cx, cy, sigma_x, sigma_y, shift=(0,0)):
"""2次元ガウス分布を返す関数"""
dx, dy = shift[0], shift[1]
return np.exp(-(((X-(cx+dx))**2)/(2*sigma_x**2)
+((Y-(cy+dy))**2)/(2*sigma_y**2)))
def flow_vector(flow, spacing, margin, minlength=-np.inf, maxlength=np.inf):
"""
フローベクトルを抽出し、可視化に適した形式に変換する。
パラメータ
----------
flow : ndarray of shape (H, W, 2)
各ピクセルにおけるフローベクトル (dy, dx)。
spacing : int
サンプリング間隔(間引きピクセル数)。
margin : int
枠から除外するマージン幅。
minlength : float, optional (default=-np.inf)
流れの最小サイズ(この値以下は無視)。
maxlength : float, optional (default=np.inf)
流れの最大サイズ(この値以上は無視)。
戻り値
-------
x : ndarray
サンプリングした x 座標。
y : ndarray
サンプリングした y 座標。
u : ndarray
各座標における x 方向ベクトル成分 (dx)。
v : ndarray
各座標における y 方向ベクトル成分 (dy)。
"""
h, w, _ = flow.shape
x = np.arange(margin, w - margin, spacing, dtype=np.int64)
y = np.arange(margin, h - margin, spacing, dtype=np.int64)
mesh_flow = flow[np.ix_(y, x)]
mag, _ = cv2.cartToPolar(mesh_flow[..., 0], mesh_flow[..., 1])
mask = (mag <= minlength) | (mag >= maxlength)
mesh_flow[mask] = np.nan
u = mesh_flow[..., 1]
v = mesh_flow[..., 0]
return x, y, u, v
import matplotlib.lines as mlines
# --------------------------
# 1. シミュレーションデータ作成
# --------------------------
H, W = 101, 101
np.random.seed(2025)
Y, X = np.mgrid[0:H, 0:W]
cx, cy = W//2, H//2
sigma = 6
# モデル
raw_model_flux = gaussian_2d(X, Y, cx, cy,
sigma_x=sigma, sigma_y=sigma,
shift=(0, 0))
# 観測
true_shift = (-4, -3) # (dx, dy)
raw_obs_flux = gaussian_2d(X, Y, cx, cy,
sigma_x=sigma, sigma_y=sigma,
shift=true_shift)
# exposure
t_obs = 100
t_model = 400
obs_exposure = np.ones((H, W)) * t_obs
model_exposure = np.ones((H, W)) * t_model
# Poissonカウント生成
raw_model_counts = np.random.poisson(raw_model_flux * model_exposure)
obs_counts = np.random.poisson(raw_obs_flux * obs_exposure)
# 規格化済みモデル
model_counts = raw_model_counts * obs_exposure / model_exposure
# --------------------------
# 2. proper motion の推定
# --------------------------
window_radius = 11
search_radius = 9
flow = estimate_proper_motion(obs_counts, model_counts,
window_radius=window_radius, search_radius=search_radius,
use_tqdm=False)
# --------------------------
# 3. 可視化 (subplots 版)
# --------------------------
# maxlength は探索範囲の端に張り付いた「不安定な解」を除外するために設定。
# search_radius ちょうどのシフトが最尤解になることがありますが、
# それは探索範囲外にさらに良い解がある可能性を示唆しています。
# 特に斜め方向ではピクセル境界の影響で不安定になりやすいため、
# 安全のために -1 をつけて search_radius-1 として解を除外しています。
x, y, u, v = flow_vector(flow, spacing=5, margin=5, maxlength=search_radius-1)
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# 共通のカラースケールを決定
vmin = min(obs_counts.min(), model_counts.min())
vmax = max(obs_counts.max(), model_counts.max())
# (1) 観測
ax = axes[0,0]
im = ax.imshow(obs_counts, origin="lower", cmap="ds9_b", vmin=vmin, vmax=vmax)
ax.set_title(f"Observed ({t_obs=})")
ax.set_xlabel("x [pixel]")
ax.set_ylabel("y [pixel]")
fig.colorbar(im, ax=ax)
# (2) 規格化モデル
ax = axes[0,1]
im = ax.imshow(raw_model_counts, origin="lower", cmap="ds9_b", vmin=vmin, vmax=vmax*t_model/t_obs)
ax.set_title(f"Raw Model ({t_model=})")
ax.set_xlabel("x [pixel]")
ax.set_ylabel("y [pixel]")
fig.colorbar(im, ax=ax)
# (3) 差分
ax = axes[1,0]
diff = obs_counts - model_counts
im = ax.imshow(diff, origin="lower", cmap="seismic",
vmin=-np.max(np.abs(diff)), vmax=np.max(np.abs(diff)))
ax.set_title("Difference (Observed - Model)")
ax.set_xlabel("x [pixel]")
ax.set_ylabel("y [pixel]")
# カラーバー
cbar = fig.colorbar(im, ax=ax)
cbar.set_label("Difference")
# 図中にラベルを追加
ax.text(0.03, 0.97, "Obs > Model", color="red",
transform=ax.transAxes, va="top", ha="left")
ax.text(0.03, 0.86, "Model > Obs", color="blue",
transform=ax.transAxes, va="bottom", ha="left")
# (4) フローベクトル
ax = axes[1,1]
ax.set_title(f"Flow field ({window_radius=}px, {search_radius=}px)")
ax.imshow(obs_counts, origin="lower", cmap="gray", alpha=0.7)
# 流れの大きさと quiver
mag = np.sqrt(u**2 + v**2)
q = ax.quiver(x, y, u, v, mag, cmap="plasma",
angles="xy", scale_units="xy", scale=1)
fig.colorbar(q, ax=ax, label="Flow magnitude [pixel]")
# 正解シフト (モデルシフトとの整合性を知りたいので符号反転させて比較)
true_flow = (-true_shift[0], -true_shift[1])
mask = (u == true_flow[0]) & (v == true_flow[1])
xx, yy = np.meshgrid(x, y)
ax.scatter(xx[mask], yy[mask], s=15, c="red", marker="o",
label=f"Correct flow (dx,dy)=({true_flow[0]},{true_flow[1]})")
ax.set_xlabel("x [pixel]")
ax.set_ylabel("y [pixel]")
ax.legend()
fig.tight_layout()
plt.show()
# --------------------------
# 4. 誤差推定
# --------------------------
# proper motion の推定(return_cstat_map=Trueにしてc-statの結果も返す)
window_radius = 11
search_radius = 9
flow, search_list, cstat_cube = estimate_proper_motion(
obs_counts, model_counts,
window_radius=window_radius, search_radius=search_radius,
use_tqdm=False, return_cstat_map=True
)
# 指定座標における ΔC マップを表示
plot_delta_c_map(search_list, cstat_cube, x0=50, y0=50)
plot_delta_c_map(search_list, cstat_cube, x0=40, y0=60)
基本例:単一構造の場合
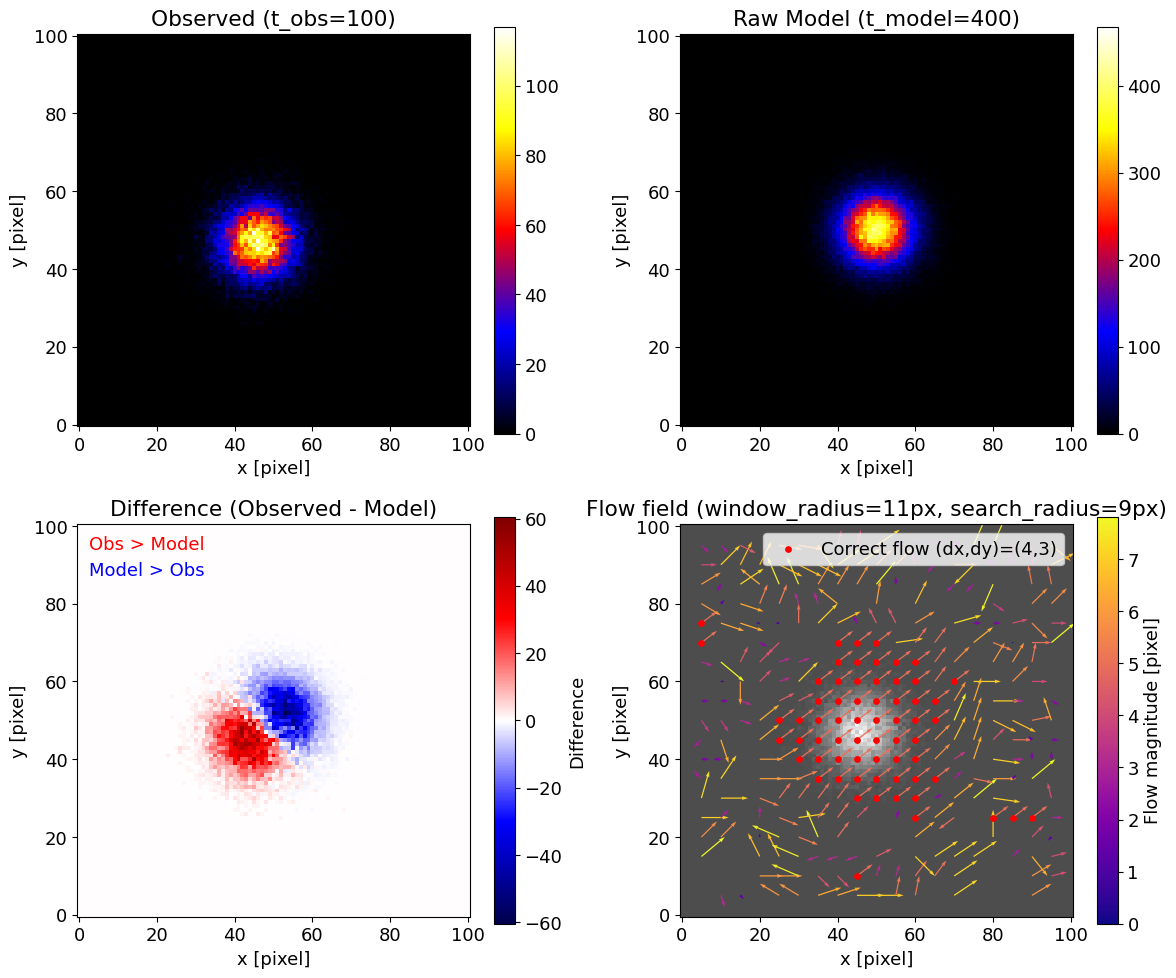
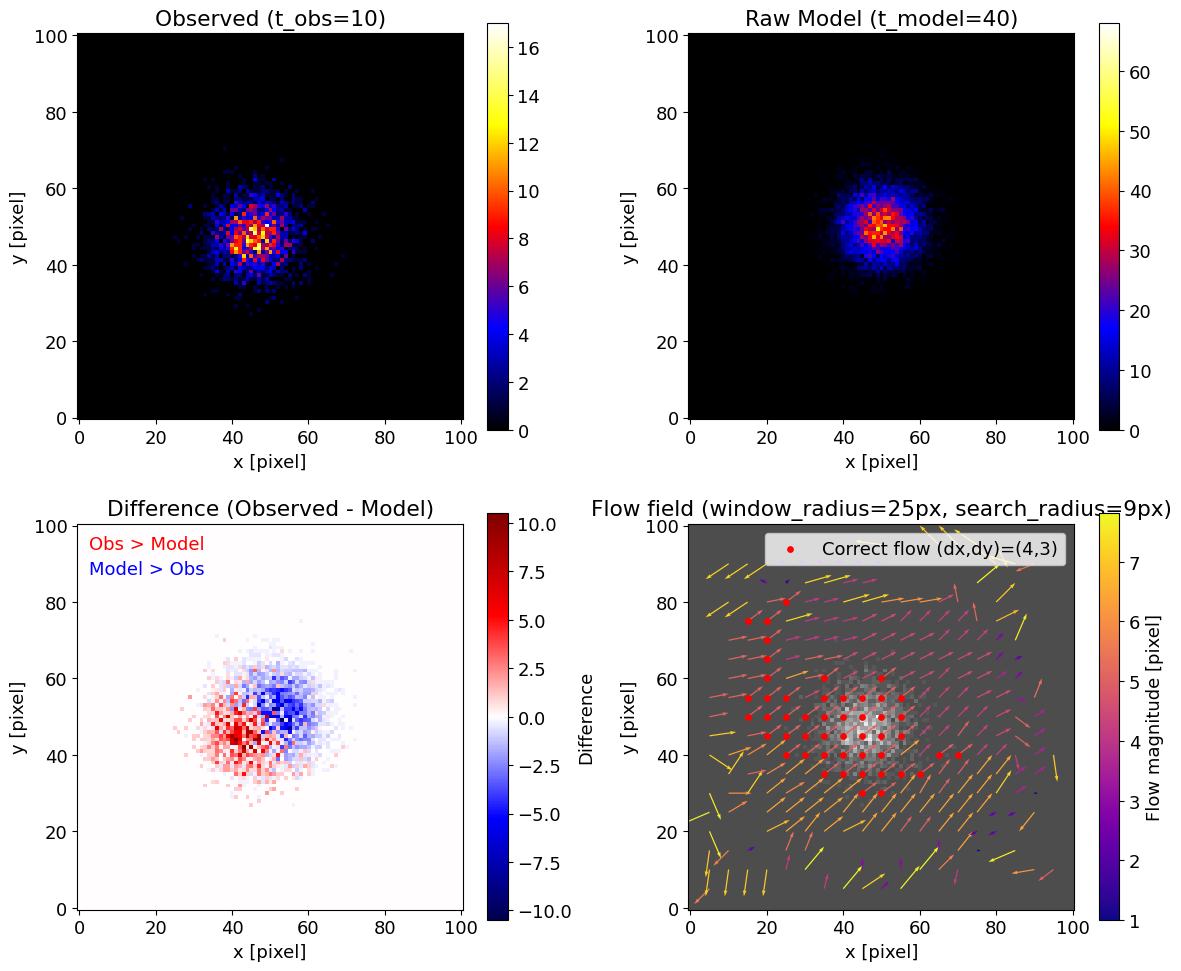
観測とモデルをそれぞれ露光時間 $t_{\rm obs}=100$, $t_{\rm model}=400$ で用意し、観測側を $(-4,-3)$ ピクセルだけシフトさせました。
両方の画像に Poisson ノイズを加えて、実際の観測に近い状況を再現しています。
- 左上:観測画像(Poisson ノイズ入り)
- 右上:生のモデル画像($t_{\rm model}$ の露光時間で得られたままのカウント数)
- 左下:観測と、観測露光時間に正規化したモデル画像との差分。赤=観測が強い、青=モデルが強い
- 右下:推定されたフローベクトル場。矢印が推定結果、赤丸が正解シフト
この例では、中心付近ではほぼ正しくシフトが推定できていることがわかります。
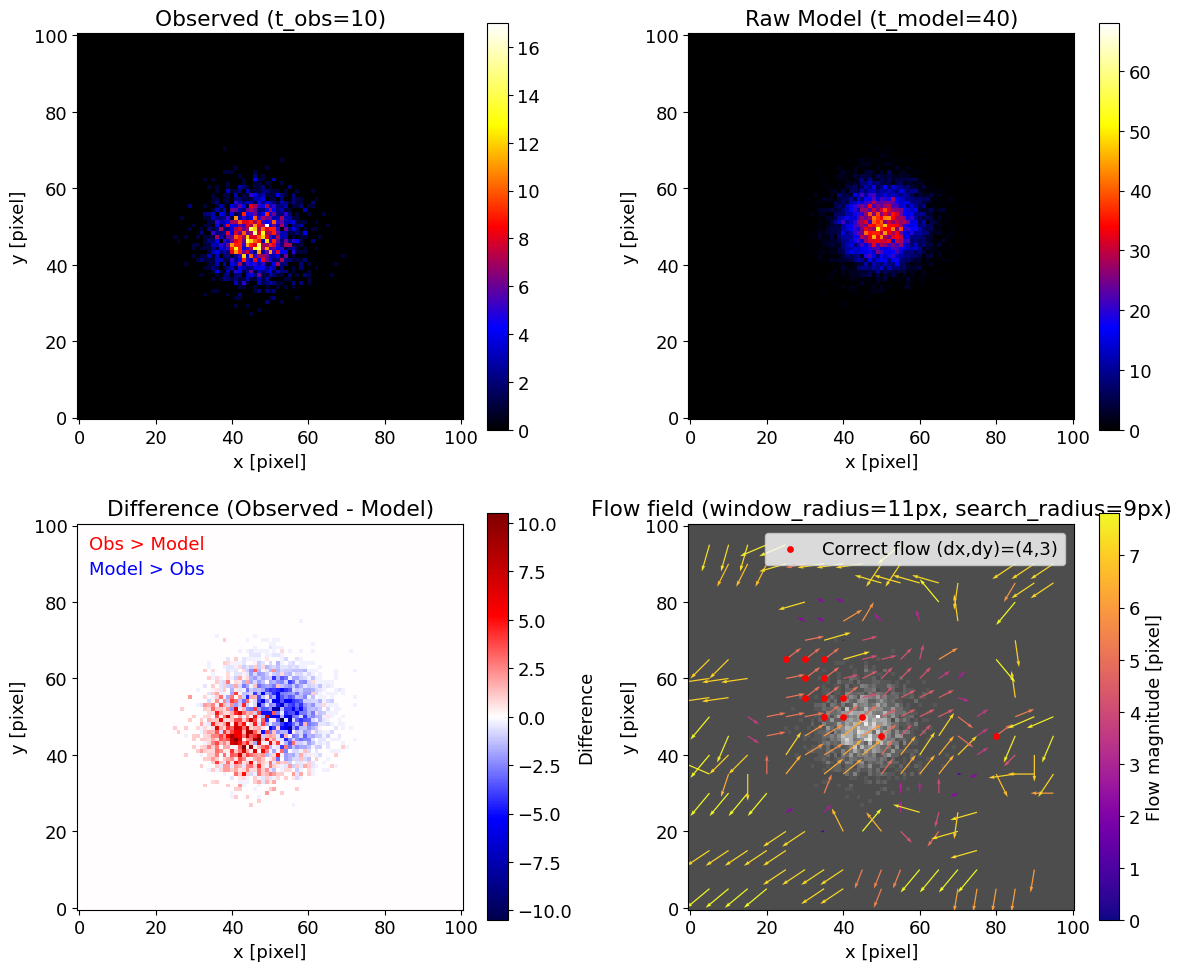
カウント不足の場合
露光時間を短い例として $t_{\rm obs}=10$, $t_{\rm model}=40$ とした場合、カウント数が少なくなるため推定は安定しない場合があります。
構造がある領域でも、正解となる固有運動を示す範囲が狭くなってしまっているのがわかります。
このような場合、窓サイズを広げることで安定性を高めることができます。
窓を広げると安定性は増しますが、その分だけ位置決定の精度は下がります。
複数構造を含む場合
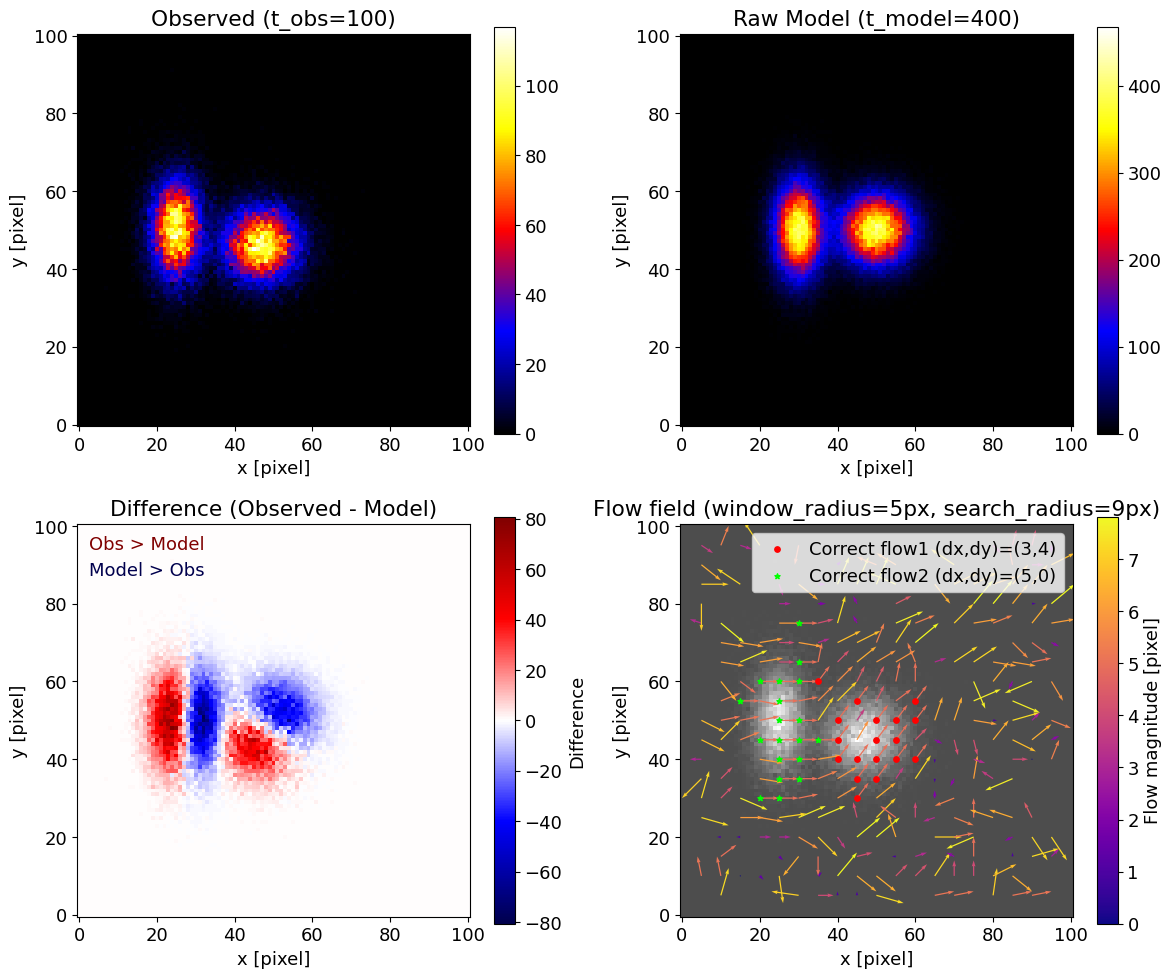
最後に、実際の天体画像を模して、2つの異なるガウス成分を重ねた例を試してみます。
このように複数の構造が存在する場合は、窓サイズの選び方が特に重要になります。
構造が込み入っていることは画像を見ればある程度わかるので、事前知識を踏まえて「半径5ピクセル程度なら適切そうだ」というあたりをつけながら窓サイズを決めます。窓を大きくしすぎると複数の構造を一度に含んでしまい、逆に小さすぎると信号が不足してノイズに埋もれてしまうためです。
実装上の注意点と解析戦略
窓サイズはどう決めるか?
窓の大きさについては「小さい方が局所の動きを正確に捉えられる」という直感が成り立ちますが、小さすぎるとノイズや局所的な揺らぎに敏感になり、どこでも一致してしまうという問題が生じます。
これは画像解析の分野では aperture problem(開口問題) と呼ばれており、例えば こちらのアニメーション(The Aperture Problem → Movie 1〜6)を見ると直感的に理解できます。
一方で、大きな窓を使うと統計的には安定しますが、複数の構造をまたいでしまうために「本来の動き」ではなく「平均的な動き」を拾ってしまうことがあります。
つまり、窓の大きさは対象の構造スケールと深く関係しており、構造よりも大きな窓を安易に使うと誤った解釈につながる点に注意が必要です。
実際の研究においても窓サイズの扱いは重要な課題となっています。例えば Sakai et al. (2024) では、超新星残骸 Cas A の解析において 場所依存的に窓サイズを調整することで推定精度を向上させる手法を検討しました。
探索範囲はどう決めるか?
どの範囲で解を探すかは重要な問題です。
X線スペクトル解析でも「観測を説明できるモデルはあっても、物理的に正しいとは限らない」と言われますが、固有運動の推定も同様です。
探索範囲を大きくとりすぎると、観測を説明できても物理的には不自然なほど大きなシフト量が最小値として得られる場合があります。これは数値的に最も適合しているだけで、必ずしも妥当な解ではありません。
また、探索範囲の端に解が現れる場合も注意が必要です。C-statistic が最小となっていても、それが真の最小値なのか、それとも探索範囲外により深い極小があるのかは判断できません。
このため、探索範囲は段階的に調整し、端に張り付いた解は慎重に扱う必要があります。本記事の実装では、そのような誤解を避けるため、探索半径に近いシフトは表示から除外しています。
モデル画像にゼロが出るとき
モデル画像も観測に基づくため、画素によってはカウントがゼロになることがあります。しかしポアソン分布では母平均がゼロは定義されないため、そのままでは $C$ 統計量に含まれる $\log \Lambda$ が計算不能になります。
この記事では簡易的な実装として、λ がゼロのときは 小さい値(例: 0.01) を代入することで計算を継続しています。
ただし、これはあくまで暫定的な回避策です。背景光の寄与を考えれば「本当にゼロの領域」は存在しにくく、背景レベルを平均的に代入する方が自然かもしれません。しかし背景は場所によって異なる可能性もあり、さらに天体の構造が重なると背景 + α となるため、どの値を入れるかは一筋縄ではいきません。
つまり ゼロの扱いは単純ではなく、解析戦略そのものに直結する難題 です。研究現場でも議論が続いており、ここでは記事を簡潔にするため簡易処理にとどめています。
モデル画像は「真の母数」ではない
比較に用いるモデル画像は、真の母数ではない点にも注意が必要です。ここでのモデルは観測を正規化して得られた近似であり、依然としてノイズを含んでいます。
したがって、モデルを用いた推定結果には誤差やバイアスが入り得ます。詳しくは こちらの記事 でも紹介していますが、モデルはあくまで観測を基にした近似として扱うのが適切です。
誤差をどう見積もるか?
最尤推定で得られた固有運動ベクトルには、当然ながら不確かさが伴います。
誤差の見積もり方としては、大きく分けて 2 つの方法があります。
1. 漸近近似に基づく方法
Cash (1979) によれば、$C$ 統計量の増分 $\Delta C = C - C_{\min}$ は漸近的に $\chi^2$ 分布に従います。
本記事ではシフト量 $(\Delta x, \Delta y)$ の2変数を推定しているため、自由度 $\nu=2$ のカイ二乗分布を仮定し、
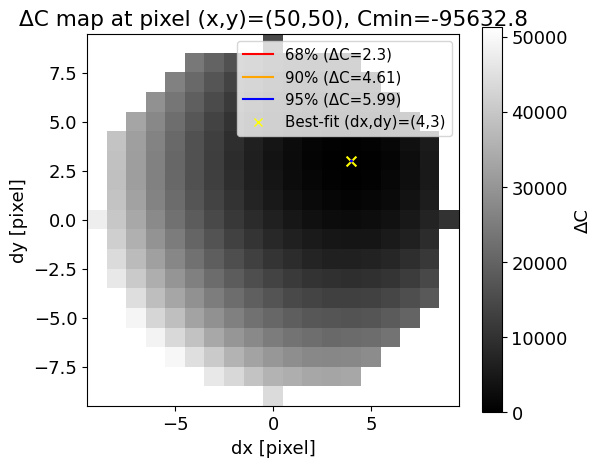
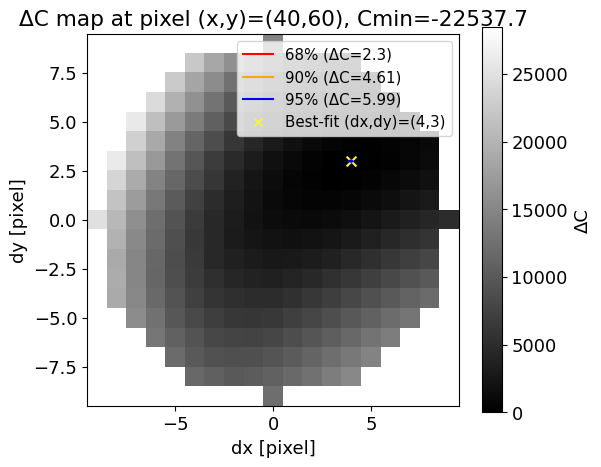
$\Delta C = 2.3, 4.61, 5.99$ を用いてそれぞれ 68%, 90%, 95% 信頼区間を評価します(実装コードは Google Colab にあります)。
例として 単一構造のケース では、以下のように可視化できます:
今回の例のように統計が良い場合は最小値($C_{\min}$)の近傍 1 ピクセル以内に収まりますが、統計量が少ない場合や複雑な構造では広がりが大きくなることもあります。その広がりを誤差として解釈します。
さらに、$C_{\min}$ の値そのものが小さいほど「モデルが観測に適合している」ことを意味します。したがって、$C_{\min}$ はフィットの良さを表す指標、広がりはその推定の不確かさを表す指標として、両方を意識して見ると良いと思います(今回の例では、構造の中心付近の方が適合度が高いことを示しています)。
2. モンテカルロ法による方法
もう一つのアプローチは モンテカルロシミュレーション です。
各画像のカウント値を平均を母数としたポアソン分布で揺らがせ、何度も固有運動を再推定することで分布を得ます。
この記事ではその実装コードは含めていませんが、比較的シンプルに導入できる誤差推定手法として用いられることがあります。
X線天文における固有運動解析の種類
ここでは、X 線天文学における代表的な固有運動法について説明します。
固有運動の推定では主に χ² フィッティング と ポアソン尤度(C-statistic) の 2 つのアプローチが使われることが多いです。
また近年では、画像処理分野の手法や物理的制約を組み込む試みも進んでいます。
以下ではそれらの手法を概観します。
χ² フィッティング
カウント数が十分に大きい場合、ポアソン分布はガウス分布で近似できるため、χ² 法が有効です。
特に画像の移動方向があらかじめ分かっている場合は、その方向に沿って一次元プロファイルを作り、差を評価する形で実装されます。
実際の研究例としては、Katsuda et al. (2008) が超新星残骸の膨張速度の測定に用いられ、
さらに Tanaka et al. (2020) では加速度の推定にも応用されています。
近年では Suzuki et al. (2022), (2023) にも受け継がれ、実務的な固有運動解析の標準的な手法となっています。
Poisson 尤度(C-statistic)
カウント数が少ない場合や、二次元的なベクトル場として運動を扱いたい場合には、ポアソン統計に基づくアプローチが有効です。
Vink et al. (2022) では、Cas A の膨張を自己相似モデルに従うと仮定して解析し、爆発環境の推定に結びつけています。
また Sakai et al. (2024) では、Cas A において数十年スケールで運動方向が大きく変化しないという制約を課すことで、解の安定性を議論しています。
画像処理的アプローチ
画像解析の手法も、近年では X 線天文学に応用され始めています。
Sato et al. (2018) は optical flow を Cas A に適用し、二次元的な流れの構造を捉えることに成功しています。
また Ichinohe & Sato (2023) では、格子点の変位を cubic B-spline で補間する方法を導入し、連続的で滑らかな変形場をモデル化しています。
この他にも、点源やブロブのような単純な構造では クロスコリレーション法 や ガウス関数フィット などがよく用いられます。
このように、固有運動解析は 「統計的な枠組み」 × 「物理的制約」 × 「画像処理的アプローチ」 が組み合わさりながら進化しています。
まとめ
本記事では、ポアソン尤度(C-statistic)に基づく固有運動解析の枠組みを紹介しました。
数式から実装、シミュレーションを通じて「窓サイズや探索範囲の選び方が結果に大きく影響する」ことを確認しました。固有運動解析は対象やデータによって工夫が必要ですが、ここでの内容が解析の参考や新しい発想のきっかけになれば幸いです。
本記事は、修士課程から取り組んできた研究を整理し直したものです。まだ模索中の部分もありますが、日々ご指導くださっている指導教官や共著者の皆様に深く感謝申し上げます。