はじめに
ポアソン分布は、光や粒子のカウント、イベント検出、到着過程など、さまざまな分野で広く使われています。
その中でよくあるのが「ある観測で得られたカウント値を、そのままポアソン分布のパラメータ $\lambda$ として使う」というやり方です。
たとえば次のようなケースです:
- 観測A(測定時間が長い)で得たカウント値を $\lambda$ とみなす
- 観測B(別の時間スケール)のカウント $k$ を、その $\lambda$ に基づいて評価する
一見すると自然な方法ですが、そもそも $\lambda$ 自体もポアソン過程から得られた観測値のひとつであり、本当の期待値(母数)であるとは限りません。もし両方の観測条件が近い場合、「片方だけをパラメータ扱いする」という前提はどこまで正当なのか?という素朴な疑問が生まれます。
とはいえ、この近似がどの程度ズレを生むのかは、手元で直感的に判断しにくい問題です。
そこでこの記事では、以下の2つのモデルを比較しながら、
- どの程度までなら近似として妥当か
- どの条件でズレが顕在化するのか
を実際に数値的に確かめることで、「なんとなく問題なさそう」と済ませていた部分が、どういう条件で破綻し始めるのか、あるいは意外と安定しているのかを視覚的に把握することを目的としています。
本記事で紹介した実装コードは、Google Colab こちら からそのまま試すことができます。
環境構築不要で動かせますので、ぜひ手元のデータやパラメータに合わせて活用してみてください。
基本的な設定
観測で得られるカウント値 $k$ はポアソン分布に従うと考えられます。
しかし、その期待値 $\lambda$ が「真の母数」かといえばそうではなく、実際には別の観測から得られた値を代用していることが多いです。
つまり 「$\lambda$ は、ある母数 $\theta$ に従うポアソン分布の実現値だったかもしれない」という視点を持つことができます。
この前提のもとで、次に2つのモデルを定式化します。
モデルの定式化
Simple Poisson(λ をそのまま固定パラメータとして扱う場合)
観測から得られたカウント値 $\lambda$ を、そのままポアソン分布の期待値として用いる近似です。観測時間などの違いをスケール係数 $s$ で補正すると、$k$ の分布は次のように書けます:
p(k \mid s,\lambda)
= \frac{(s\lambda)^k e^{-s\lambda}}{k!}
ここで
\lambda' = s\lambda
とおけば、
p(k \mid s,\lambda) = p(k \mid \lambda')
= \frac{(\lambda')^k e^{-\lambda'}}{k!}
となります。
このモデルでは $\lambda$ は確率変数とはみなさず、観測値などから与えられた定数として扱います。実務上は「代表的な観測値をそのままパラメータに代入する」形で広く用いられています。
Double Poisson(λ に揺らぎがある場合)
一方で、$\lambda$ 自体も本来はポアソン過程から得られた観測量と考えることができます。その場合、$\lambda$ の背後にある母数 $\theta$ を用いて次のような分布を仮定できます:
p(\lambda \mid \theta) = \frac{\theta^\lambda e^{-\theta}}{\lambda!}
この $\lambda$ に対する揺らぎを考慮すると、$k$ の分布は周辺化によって次のように定義されます(これをここでは Double Poisson と呼びます):
p(k \mid s,\theta)
= \sum_{\lambda=0}^\infty p(k \mid s,\lambda)\, p(\lambda \mid \theta).
すなわち、
p(k \mid s,\theta) =
\sum_{\lambda=0}^\infty
\frac{(s\lambda)^k e^{-s\lambda}}{k!}
\cdot
\frac{\theta^\lambda e^{-\theta}}{\lambda!}.
このように書くことで、Simple Poisson との差がはっきりします:
- Simple Poisson:$\lambda$ を固定して使う
- Double Poisson:$\lambda$ を確率変数とみなし、$\theta$ に基づき周辺化する
観測条件が近い場合や統計量が十分でない場合には、この違いが無視できなくなることがあります。
数値的な比較
Double Poisson モデルは解析的に閉じた式を得るのが難しいため、ここでは数値積分を用いて確率分布を計算します。
以下に Python による実装例を示します。
比較を分かりやすくするため、基準となる期待値を $\lambda' = 7.5$ とし、観測時間の比率を表すスケール係数 $s$ を変化させながら結果を見ていきます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammaln, logsumexp
plt.rcParams["font.size"] = 14
# ---- Simple Poisson ----
def poisson_prob(k, lam):
return np.exp(k * np.log(lam) - lam - gammaln(k + 1))
# ---- Double Poisson (離散和) ----
def double_poisson_prob_discrete(k, theta, s, lam_max=None):
"""
Double Poisson probability with discrete summation.
lam_max を None にすると θ+5√θ まで自動で打ち切る
"""
if lam_max is None:
lam_max = int(theta + 5 * np.sqrt(theta)) # だいたい十分
lam = np.arange(lam_max + 1)
log_terms = (
k * np.log(s * lam + 1e-300) - s * lam
- gammaln(k + 1)
+ lam * np.log(theta) - theta
- gammaln(lam + 1)
)
return np.exp(logsumexp(log_terms))
# ---- k の範囲 ----
k_values = np.arange(0, 50)
# ---- Simple Poisson(比較用) ----
theta_base = 7.5
simple_probs = [poisson_prob(k, theta_base) for k in k_values]
# ---- Double Poisson のパラメータセット ----
param_sets = [
(7.5, 1.0),
(15.0, 0.5),
(75.0, 0.1)
]
# ---- プロット開始 ----
plt.figure(figsize=(8, 6))
# Simple Poisson(基準)
plt.plot(
k_values,
simple_probs,
label=f"Simple Poisson (λ'={theta_base})",
linestyle="--",
linewidth=2
)
# Double Poisson を 3 種類重ね描画
for theta, s in param_sets:
double_probs = [double_poisson_prob_discrete(k, theta, s) for k in k_values]
plt.plot(
k_values,
double_probs,
label=f"Double Poisson (θ={theta}, s={s})"
)
# 軸・凡例
plt.xlabel("k")
plt.ylabel("Probability")
plt.title("Simple Poisson vs Double Poisson (Discrete Summation)")
plt.legend()
plt.tight_layout()
plt.show()
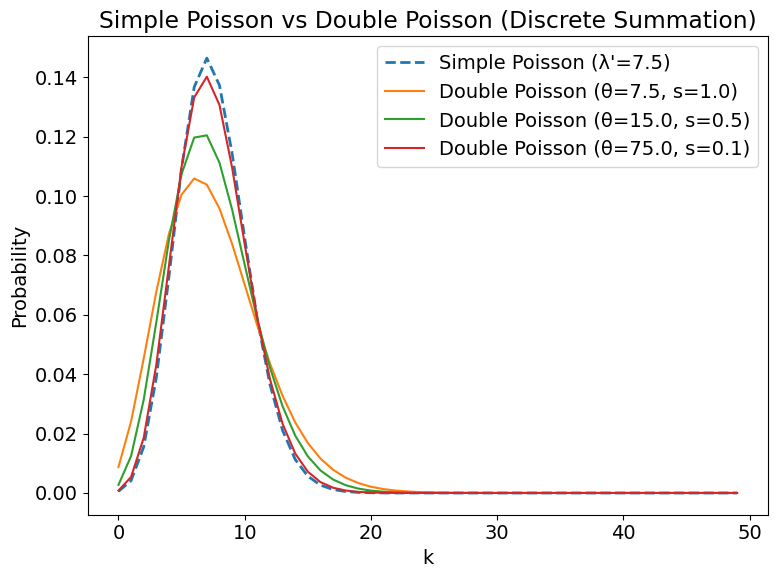
出力結果
結果の解釈
計算結果を比べると、スケール係数 $s$ によって Simple Poisson と Double Poisson の一致度合いが大きく変わることが分かります。
-
$s = 1$(観測側とモデル側が同じ観測時間の場合)
→ 両分布はほぼ完全に一致し、違いは見られません。 -
$s = 0.5$(モデル側の観測時間が2倍長い場合)
→ Simple Poisson と Double Poisson の間に中程度の差が現れます。観測を2倍モデルで補正するイメージに近いです。 -
$s = 0.1$(モデル側の観測時間が10倍長い場合)
→ 両分布の差はほとんど消え、Simple Poisson で十分近似できます。
まとめ
今回見てきたように、ポアソン分布を使うときに $\lambda$ を「そのままパラメータ」として扱うと、観測時間が短い場合には $\lambda$ 自体の持つ誤差によってズレが生じることがあります。
そこで Double Poisson のように揺らぎを含めたモデルを考えると、「どの程度ズレが出るのか」を簡易的に確かめることができます。もちろん実際には、その背後にある真のパラメータを直接知ることはできませんが、こうした見方を通じて「誤差のイメージ」を掴むことはできます。
ポアソン分布に限らず、どんなモデルでも大切なのは「現実とのズレがどの程度あるか」を意識することだと思います。この記事が、ポアソン近似による影響を考えるきっかけになれば幸いです。