回帰の誤差、２乗するか絶対値をとるか

概略

関数の回帰のとき、損失関数を誤差の2乗の和にするか絶対値の和にするかですが、回帰した結果が

• 差の2乗の合計：データ分布の平均
• 差の絶対値の合計：データ分布の中央値

となることを確認しました。

対象

$$
x(x^2 - 1) = y
$$

という３次式に適当にノイズを乗せ、

$$
f(x; a, b, c, d) = ax^3 + bx^2 + cx + d
$$

でフィットしてみます。回帰パラメータは係数、$a, b, c, d$です。

このノイズの分布において、回帰関数は平均値・中央値のどこら辺に落ち着くかを見てみます。

損失関数

• ２乗誤差

$$
L_\mathrm{square}(x, y; a, b, c, d) = \sum_i\left(y_i - f(x_i; a, b, c, d)\right)^2
$$

• 絶対値誤差

$$
L_\mathrm{abs}(x, y; a, b, c, d) = \sum_i\left|y_i - f(x_i; a, b, c, d)\right|
$$

なんの変哲もない損失関数の定義かと思います。

実装と結果

準備

ライブラリ

import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

３次関数

def f(x, a, b, c, d):
    return a*x**3 + b*x**2 + c*x + d

これについて、xはndarray配列、a, b, c, dはただのfloatが入る予定です。

データ列の準備

def make_samples(N, a, sigma=0.05, xmin=-1, xmax=1):
    x = np.linspace(xmin, xmax, N)
    return x, np.random.normal(f(x, a, 0.0, - a*0.5, 0.0), sigma, size=N)

これはサンプル列としてndarray配列x, yを返します。

呼び出し例と確認

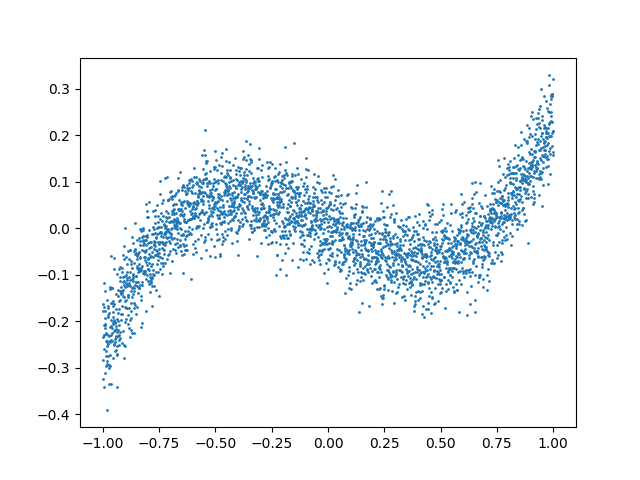
    x, y = make_samples(3000, 0.5) 
    plt.scatter(x, y, s=1)
    plt.show()

誤差の分布も出力してみました。

まあ正規分布になっているかなと思います。

最小化

scipy.optimizeのminimizeを使います。
$a, b, c, d$の初期値は適当に$(1, 0, 0, 0)$とします。

• ２乗誤差

def L_square_minimize(x, y):
    init = np.array([1.0, 0.0, 0.0, 0.0])
    def loss(args):
        a, b, c, d = args
        return np.sum(0.5*(y - f(x, a, b, c, d))**2)
    ret = minimize(loss, init)
    return  ret["x"]

• 絶対値誤差

def L_abs_minimize(x, y):
    init = np.array([1.0, 0.0, 0.0, 0.0])
    def loss(args):
        a, b, c, d = args
        return np.sum(np.abs(y - f(x, a, b, c, d)))
    ret = minimize(loss, init)
    return  ret["x"]

L_square, L_abs どちらも、１次元で長さNのndarray配列xとyを受け取り、フィットしたパラメータ $a, b, c, d$ を返します。

loss中のfに渡しているxはndarrayで、aからdはminimize中で最適化中のパラメータです。

実行

def main():
    x, y = make_samples(3000, 0.5) 

    sq_p = L_square_minimize(x, y)
    abs_p = L_abs_minimize(x, y)

    print("Minimize square loss: ({}) x**3 + ({}) x**2 + ({}) x + ({}) = y".format(*sq_p))
    print("Minimize absolute loss: ({}) x**3 + ({}) x**2 + ({}) x + ({}) = y".format(*abs_p))

出力

Minimize square loss: (0.5024932610686912) x**3 + (-0.0026207180970209062) x**2 + (-0.24999001968629547) x + (-0.00033071957587381406) = y
Minimize absolute loss: (0.4979255174265226) x**3 + (-0.0005586381675982033) x**2 + (-0.24843328425212305) x + (-0.0006657675223310448) = y

結果のパラメータの数値だけ見ると、２乗と絶対値でほとんど変わりませんね。

誤差の計算と確認

確認方法ですが、回帰した関数と真値との差をサンプル全体でみて、その差の平均値が０なら回帰した関数はサンプルの平均値を見ていて、中央値が０なら中央値に回帰していると考えます。関数の形がまだそんなにややこしくないので、これで大丈夫かなと。

    fit_sq = f(x, sq_p[0], sq_p[1], sq_p[2], sq_p[3])
    fit_abs = f(x, abs_p[0], abs_p[1], abs_p[2], abs_p[3])
    error_sq = y - fit_sq
    error_abs = y - fit_abs

    print("Square: Error mean = {}, median = {}".format(np.mean(error_sq), np.median(error_sq)))
    print("Absval: Error mean = {}, median = {}".format(np.mean(error_abs), np.median(error_abs)))

出力

Square: Error mean = 7.485378837361148e-09, median = 0.00031691672538972093
Absval: Error mean = -0.00035276293742007365, median = 1.5704008083892995e-06

２乗誤差の方は平均がほぼ０、絶対値誤差では中央値がほぼ０になっていることが確認できました。が、そうでない方もあまり大きくはありません。
とりあえず、ちゃんと回帰はできているようです。

グラフ描画

    plt.scatter(x, y, s=1)
    plt.plot(x, fit_sq, label="minimize squared L")
    plt.plot(x, fit_abs, label="minimize absolute L")
    plt.legend()
    plt.show()

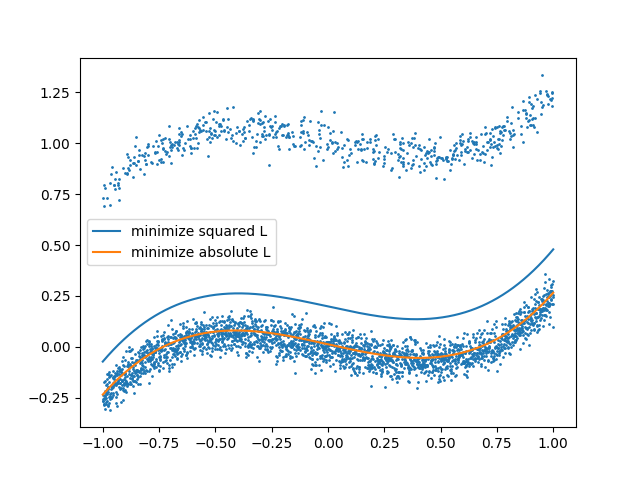
図でみると２つの誤差関数をもとに最小化した場合で差がほとんど見えませんね。

ノイズの分布の変更

先ほどの例のノイズは普通の正規分布で、平均値と中央値が一致していました。これをずらしたノイズを考えてみます。

ふた山ノイズ生成

def make_samples2(N, a, sigma=0.05, xmin=-1, xmax=1):
    offset = np.zeros(N)
    mask = np.random.rand(N) < 0.2
    offset[mask] = 1.0
    x = np.linspace(xmin, xmax, N)
    return x, np.random.normal(f(x, a, 0.0, - a*0.5, 0.0) + offset, sigma, size=N)

20％の割合でxy平面で上に１ずれるようにします。

分布をみると２つの正規分布の和で、高さが異なるので平均値と中央値がずれるようになります。

Noise average = 0.19983994665313767
Noise median = 0.013205082869315616

損失関数最小化

さっきのと同じです。

結果

出力

Minimize square loss: (0.5169492952572832) x**3 + (0.004766657455387494) x**2 + (-0.24132826196093088) x + (0.19824999318107048) = y
Minimize absolute loss: (0.4982556245394046) x**3 + (0.0032733811955541164) x**2 + (-0.24801097149238918) x + (0.01226739280297712) = y
Square: Error mean = 8.043188911048086e-09, median = -0.18530803483732208
Absval: Error mean = 0.1864806991243788, median = 2.5998962142892434e-07

両者で定数項dが特に大きく異なることが分かります。また２乗誤差の中央値、絶対値誤差の平均値がそれなりに大きな値になりました。一方で２乗誤差の平均値、絶対値誤差の中央値は０に近いままです。

もうひとつ図から分かることとして、

• ２乗誤差だと上にずれたサンプル群に引っ張られる。
• 絶対値誤差だとサンプル数が多い下のサンプル群をしっかり見ている。

その他

外れ値

一般に、最小二乗法は外れ値に弱いとされています。一方で絶対値の誤差にすると強くなり、ロバスト回帰の１つとして使われたりするようです。まあ、外れ値に対する平均値と中央値の性質に準拠しているようにも見えます。

参考：https://biolab.sakura.ne.jp/robust-regression.html

関数の非線形性

よく例で見かけるのはパラメータが１個の１次関数が多いように思ったので、頑張ってパラメータが複数で関数も線形でないものでやってみました。
なおノイズを$bx^2$の項に乗せてみた場合も試してみましたが、それでも傾向は同様でした。

ややこしいニューラルネットワークでの回帰タスクでも同様の傾向ではないかなと思います。

メリットとデメリット

これだけ見ると損失関数を2乗にすると外れ値に弱くなるだけでよくないように見えますが、最小二乗法はアルゴリズムが行列演算の形で高度に整備されていて、線形な関数ならイテレーションもいらないという利点が考えられます。
最小二乗法の適用前にトンプソン検定などでデータをチェックして外れ値の除去をするとかの工夫もあるようです。
そもそも今回の外れ値を導入したケースでは最小二乗法の前提に適しておらず、例としてよくないとも言えます。

一方で絶対値誤差の方は、$x = 0$で微分ができないというのがあり、劣微分を考えても微分係数が一意に定まらなくなります。
今回はなんかうまくいきましたが・・・。

正則化

機械学習とか統計で、L2正則化（リッジ回帰）とかL1正則化（LASSO）とかを思い出すかもしれませんが、数学的には違う話かなと思います。

「〜かと思います」多くない？

ほとんど独学なもので・・・断言するだけの自信を持てません。すみません。

探し物

２乗誤差の損失関数最小化がサンプル分布の平均値になり、絶対値誤差の損失関数最小化が中央値になるというのを数学的にちゃんと導いている講義用pdfを見かけた気がするのですが、失念してしまいました。

ブログ記事なら見つけた。
http://tsujimotter.hatenablog.com/entry/2013/11/17/201051

ほかにも

誤差関数で２乗、絶対値のほか一定以上の誤差で１、以内なら０とする０１型単純損失（L0ノルムっぽいの）だと最頻値になるとか。

ほかにも　２

変更したノイズの分布、なんか混合ガウス分布とするのが良さそうな気がしました。
EMアルゴリズムの練習がてら、気が向いたらやってみます。

結論

サンプルをきれいにしてから最小二乗法を使うのがいいのかな、と。

追記

補足記事を書きました。
https://qiita.com/sage-git/items/a2e0a54afbd849cdd415