あらすじ
Tensorflowで、勾配法とかで自動微分するときに途中で行列の対角化(固有値)を求めるところがあっても問題なく自動微分と勾配法による最小化ができるようです。
GradientTape を使って手動で apply_gradient する方法、自動的に微分して損失関数を minimize する方法も付けました。
Version
- Tensorflow 2.1.0
- Python 3.7.3 (Anaconda)
- Windows 10
要点
適当な3行3列の行列 $A$ を用意して、その固有値 $\lambda$ を計算したとき、最小の固有値 $\lambda_0$ に対する行列 $A$ の各成分での微分 $d\lambda_0/dA$ (成分ごとなので3行3列の行列です)を計算したいとき。
以下のコードで $d\lambda_0/dA$ を計算できます。Eagerモードですので、微分計算のための計算グラフを把握させるために GradientTape() を使います。
import tensorflow as tf
A = tf.random.uniform(shape=(3, 3))
with tf.GradientTape() as g:
g.watch(A)
val, vec = tf.linalg.eigh(A)
val0 = val[0]
grad0 = g.gradient(val0, A)
print(A)
print(val)
print(grad0)
tf.Tensor(
[[0.6102723 0.17637432 0.38962376]
[0.3735156 0.6306771 0.19141042]
[0.34370267 0.7677151 0.4024818 ]], shape=(3, 3), dtype=float32)
tf.Tensor([-0.25994763 0.34044334 1.5629349 ], shape=(3,), dtype=float32)
tf.Tensor(
[[ 5.3867564e-04 0.0000000e+00 0.0000000e+00]
[ 3.0038984e-02 4.1877732e-01 0.0000000e+00]
[-3.5372321e-02 -9.8626012e-01 5.8068389e-01]], shape=(3, 3), dtype=float32)
最後、下半分しか非ゼロになってないので、 eigh は下半分のみを使っているのではと推測されます。
実は要点といいつつ val0 = val[0] という、 slice 演算をしています。つまり固有値を求める演算以外もしています。固有値を1つ切り出さず g.gradient(val, A) というのも問題なく動作するのですが・・・数式での説明のしやすさを優先しました。
あと、val0 = val[0] ですが、 GradientTape()環境内で行っています。このように微分をつなげてほしい演算はすべてこの環境内でしないと、 g.gradient() が None を返すようになります。
応用
自動微分ゆえ、前後に演算を挟んでいくことも可能です。以降はそれを試してみます。
状況
ある6つの値を用意し、これを対称行列にならべ、固有値を計算します。これをある条件に当てはまるか、その誤差を計算して誤差関数とし、これを微分します。
- 固有値前の演算:行列の構成
- 固有値後の演算:固有値と目的の値との誤差の合計
ついでに、Tensorflow という機械学習のライブラリらしく、勾配法で元の値を更新してみます。
$r$ は3x3対称行列の成分6個を保持、 $t = (t_0, t_1, t_2)$ は目指す固有値たちとします。
r = \left(r_0, r_1, \cdots, r_5\right)
これを並べ替えて
A_h=\left(\begin{array}{ccc}
\frac{1}{2} r_0 & 0 & 0 \\
r_3 & \frac{1}{2} r_1 & 0 \\
r_5 & r_4 & \frac{1}{2} r_2
\end{array}
\right)
A = A_h + A_h^T
として行列 $A$ を構成、これの固有値を求めます。 $\lambda = (\lambda_0, \lambda_1, \lambda_2)$ を $A$ の3つの固有値を並べたものとすると、
L = \sum_{i=0}^2\left(t_i - \lambda_i\right)^2
を損失関数とします。$r$ を学習させるためには、
\frac{\partial L}{\partial r_n} = \sum_{i,j,k}\frac{\partial A_{ij}}{\partial r_n}\frac{\partial \lambda_k}{\partial A_{ij}}\frac{\partial L}{\partial \lambda_k}
が必要な計算です。真ん中の $\frac{\partial \lambda_k}{\partial A_{ij}}$ が、行列の成分による固有値の微分です。
解析的には $\det(A - \lambda I)=0$ の解 $\lambda$ を求めたら計算できますが、正直3次元を超えると、よほどの疎行列でないともう手に負えないかと。なので、数値計算のできるtensorflowに頼ります。
手動による微分呼び出し
まずめんどくさいけど処理を追える方法。
準備
r = tf.Variable(initial_value=tf.random.uniform(shape=[6]))
t = tf.constant([1.0, 1.0, 1.0])
r は3x3対称行列の成分6個を保持、 t は目指す固有値たちです。ここでは初期値として r に一様乱数を与えました。 また t はすべて1です。
自動微分のための計算
with tf.GradientTape() as g:
g.watch(r)
A = 0.5*tf.linalg.diag(r[0:3])
A = A + tf.pad(tf.linalg.diag(r[3:5]), [[0, 1], [1, 0]], "CONSTANT")
A = A + tf.sparse.to_dense(tf.sparse.SparseTensor(indices=[[0, 2]], values=[r[5]], dense_shape=(3, 3)))
A = A + tf.transpose(A)
eigval, eigvec = tf.linalg.eigh(A)
d = tf.reduce_sum((eigval - t)**2)
ここからの処理は自動微分の対象のため、 GradientTape の中でやります。
A の特定の成分を r から代入する方法として、紹介のために diag を使う方法とSparseTensor を使う2通りを使いました。
対角成分3つとその1つとなりの2つの成分を並べる関数として、tf.linalg.diagを使いました。
ただ、対角成分から1つとなりのところに並べるために pad を使っていますが、これは k オプションを使って対角から k ずれたところに並べるオプションがドキュメントでは紹介されていて、それを使うと
A = A + tf.linalg.diag(r[3:5], k=1)
と書けますが、なんか k オプションが動作しませんでした。なのでわざわざ pad を使っています。
また、 $r_5$ の1つだけを行列の角にセットする方法として、 Tensor には numpyのようなインデックス指定のassignはないので、面倒ですが疎行列を経由して足し合わせることでセットしました。
A を構成したあとは普通に対角化の eigh と損失関数の計算です。ここでは損失関数 $L$ を d としています。ややこしくてすみません。
微分の計算
grad_dr = g.gradient(d, r)
改めて、 d は損失関数 $L$ のことです。
grad_dr に長さ6のテンソルが代入されます。これでこの記事の目的は達成されました。
値の更新
適当なオプティマイザを使います。
opt = tf.keras.optimizers.Adam()
opt.apply_gradients([(grad_dr, r), ])
ここで微分が使えるからと、
opt.minimize(d, var_list=[r])
とすると、
TypeError: 'tensorflow.python.framework.ops.EagerTensor' object is not callable
というエラーが出ます。これは第一引数の d が Tensor ではなく、損失関数を返す引数なしの関数であることを要求されているからです。こっちの方法は後述します。
出力例
たとえば初期の r が
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([0.12108588, 0.8856114 , 0.00449729, 0.22199583, 0.8411281 ,
0.54751956], dtype=float32)>
のとき、Aは
tf.Tensor(
[[0.12108588 0.22199583 0.54751956]
[0.22199583 0.8856114 0.8411281 ]
[0.54751956 0.8411281 0.00449729]], shape=(3, 3), dtype=float32)
となります。すると損失関数の微分 $\frac{dL}{dr}$ は
tf.Tensor([-1.757829 -0.22877683 -1.991005 0.88798404 3.3645139 2.1900787 ], shape=(6,), dtype=float32)
と計算されました。これを opt.apply_gradients([(grad_dr, r), ]) という感じで適用すると r の値は
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([0.12208588, 0.8866114 , 0.00549729, 0.22099583, 0.8401281 ,
0.5465196 ], dtype=float32)>
となっていて、最初の値 [0.12108588, 0.8856114 , 0.00449729, 0.22199583, 0.8411281, 0.54751956]から若干変わっていることがわかります。
収束へ
せっかくなんで繰り返してみます。もし最適化が成功すれば t で設定したように固有値がすべて1の対称行列が得られるでしょう。
while d > 1e-8:
with tf.GradientTape() as g:
g.watch(r)
A = 0.5*tf.linalg.diag(r[0:3])
A = A + tf.pad(tf.linalg.diag(r[3:5]), [[0, 1], [1, 0]], "CONSTANT")
A = A + tf.sparse.to_dense(tf.sparse.SparseTensor(indices=[[0, 2]], values=[r[5]], dense_shape=(3, 3)))
A = A + tf.transpose(A)
eigval, eigvec = tf.linalg.eigh(A)
d = tf.reduce_sum((eigval - t)**2)
grad_dr = g.gradient(d, r)
opt.apply_gradients([(grad_dr, r), ])
print("---------------")
print(r)
print(eigval)
print(d)
d が2乗誤差で、これが一定以下になるまで while ループで繰り返しています。
これを実行すると
---------------
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([0.10630785, 0.18287621, 0.14753745, 0.16277793, 0.7271476 ,
0.08771187], dtype=float32)>
tf.Tensor([-0.56813365 0.07035071 0.9315046 ], shape=(3,), dtype=float32)
tf.Tensor(3.3279824, shape=(), dtype=float32)
---------------
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([0.10730778, 0.18387613, 0.14853737, 0.16177836, 0.72614765,
0.0867127 ], dtype=float32)>
tf.Tensor([-0.5661403 0.07189684 0.9309651 ], shape=(3,), dtype=float32)
tf.Tensor(3.3189366, shape=(), dtype=float32)
---------------
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([0.10830763, 0.18487597, 0.1495372 , 0.1607792 , 0.72514784,
0.08571426], dtype=float32)>
tf.Tensor([-0.564147 0.07343995 0.9304282 ], shape=(3,), dtype=float32)
tf.Tensor(3.3099096, shape=(), dtype=float32)
以下略
という感じで、 r と A が少しずつ変わっていることが見て取れます。収束まですると、
<tf.Variable 'Variable:0' shape=(6,) dtype=float32, numpy=
array([ 9.9999946e-01, 9.9999988e-01, 9.9999732e-01, 6.9962436e-05,
4.2644251e-07, -1.1688111e-14], dtype=float32)>
tf.Tensor([0.9999294 0.9999973 1.0000702], shape=(3,), dtype=float32)
tf.Tensor(9.917631e-09, shape=(), dtype=float32)
となりました。A はおおよそ単位行列のようですね。何度かやっても同様だったので、固有値が 1 だけの行列をこの方法で求めると単位行列に行き着くようです。
一応ループ回数をカウントしてみますと、3066とか2341とか3035とか、数千ステップかかるようです。
自動で微分と更新処理をやってもらう方法
要は minimize() を使う方法です。
対称行列 A の構成については、上の方の「自動微分のための計算」節を参考にしてください。
r = tf.Variable(initial_value=tf.random.uniform(shape=[6]))
t = tf.constant([1.0, 1.0, 1.0])
def calc_eigval(r):
A = 0.5*tf.linalg.diag(r[0:3])
A = A + tf.pad(tf.linalg.diag(r[3:5]), [[0, 1], [1, 0]], "CONSTANT")
A = A + tf.sparse.to_dense(tf.sparse.SparseTensor(indices=[[0, 2]], values=[r[5]], dense_shape=(3, 3)))
A = A + tf.transpose(A)
eigval, eigvec = tf.linalg.eigh(A)
return eigval
def calc_loss(r):
eigval = calc_eigval(r)
d = tf.reduce_sum((eigval - t)**2)
return d
opt = tf.keras.optimizers.Adam()
loss = lambda: calc_loss(r)
while d > 1e-8:
opt.minimize(loss, var_list=[r])
print("---------------")
print(r)
print(calc_eigval(r))
print(calc_loss(r))
calc_eigval は固有値を返す関数、 calc_lossは損失関数を計算する関数です。
loss は関数で loss() とするとこの時点での r の値に基づいて損失関数を計算し、その Tensor を返す関数です。
minimize の第1引数はこういう引数なしの関数を要求しています。だから
gradientTape で計算していた d を minimize に渡してもエラーが出ていたのでした。
calc_eigval は calc_loss の中に書いてしまってもいいのですが、ループ中に固有値もどう変化しているか見たかったので別の関数を用意しました。
def calc_loss(r) と loss = lambda: calc_loss(r) が minimize 利用のためのポイントです。calc_lossをはじめから引数なしで定義すればそのままminimizeに渡せた気がしないでもない。
ともかく、これで自分でを管理しなくても良くなりました。
上のコードをそのまま main 関数とかでくくって実行すると、収束の様子が出力されます。
その他
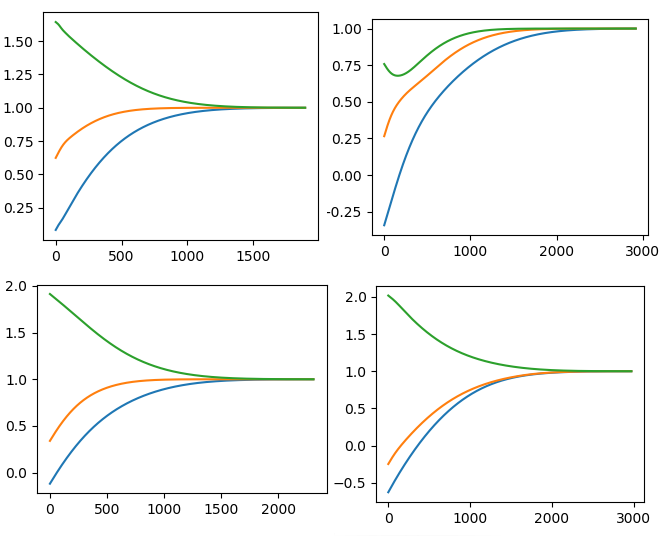
おまけで固有値の収束の様子を、ランダムな初期値で始めた4パターンほど。線はそれぞれ固有値1、固有値2、固有値3です。
右端は収束の目標とした 1 で、ちゃんと動いていることが分かります。
GradientTape() を入れ子にすることで高次微分も可能だとのこと。思ったより自動微分のカバー範囲は広いようです。
なんで GradientTape メインの記事かというと、はじめ minimize を使う方法が分からず、手動で apply_gradient するしかないと思っていたからです。記事を大半書き終えてから minimize での方法が分かりました。