概要
Prophet は「高度な専門知識を持たなくとも簡単に」時系列予測モデルを作成できるようにする、というコンセプトで作成されました。実際、Prophet は伝統的な周期・トレンド・ノイズ成分の分解に構造変化の要素を加えただけのシンプルなモデルを扱いますが、様々な時系列に柔軟に対応でき、かつ非常に手軽に使用できます。
しかし、あとほんの少しだけ時系列分析に関する知識があれば、Prophetを使ったデータ分析のクオリティを一層向上させられます。例えば以下2つの記事は、Prophet を使って時系列分析をしています。
- @haltaro さんの あまりに暑いので,140年分の気温をProphetで分析した
- @HotAllure さんの 「あまりに暑いので,140年分の気温をProphetで分析した」かったが、先を越されていたので掘り下げてみた
どちらも興味深い記事ですが、時系列分析をする際の定石が抜けており、そこを補えばさらに深い分析ができると思います。断っておきますが、コケにしたいとか、限られた人にしか分からないような小難しい数学の定理をひけらかして自分の優位を示したいとか、そういう意図はありません。上記の記事での分析を例にして、今回、説明するテクニックは、 Prophet のコンセプトに反しないよう、(やや厳密さに欠けますが) 高度な知識を持っていることを前提としない方法です。
残差診断とは
今回説明するのは残差診断です。 残差 (residuals) とは、実現値と予測値の差であり、いわばモデルと現実の誤差です。データのレコード1件1件に対して存在するため、回帰分析では決定係数とか平均二乗誤差 (MSE) とか、1つの集約された値で見られることが多いですが、残差をうまく視覚化することで、モデルをどう修正すれば良いかを知ることができます。これを残差診断といいます。
まずは準備として、モデルをフィットさせて残差を求めるところまでやります1。なお、私はグラフ作成に matplotlib ではなく plotnine をよく使いますので、以下でも読み込んでいます。
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from plotnine import ggplot, aes, theme, labs
from plotnine.geoms import *
from plotnine.scales import *
from plotnine.facets import *
from plotnine.stats import *
from plotnine.themes import *
import plotnine
from fbprophet import Prophet
from fbprophet.diagnostics import cross_validation
from fbprophet.diagnostics import performance_metrics
from fbprophet.plot import plot_cross_validation_metric
# data ディレクトリのパス。 data 以下に 'raw' ディレクトリがあるという前提
data_dir = Path().cwd() / 'data'
# データ読み込み
all_data = pd.concat(
[pd.read_csv(
file,
encoding='cp932',
skiprows=6,
header=None,
names=['date', 'average', 'high', 'low'],
usecols=[0, 1, 4, 7],
) for file in (data_dir / 'raw').glob('*.csv')]
)
all_data['date'] = pd.to_datetime(all_data['date'])
all_data.dropna(how='all', inplace=True)
all_data = all_data.set_index('date')['1875-06-10':] # 最初の数年は欠損なので削除
all_data.reset_index(inplace=True)
ave_data = all_data[['date', 'average']].rename(
columns={'date': 'ds', 'average': 'y'})
# the model by haltaro
model_haltaro = Prophet(weekly_seasonality=False)
model_haltaro.fit(ave_data)
data_result_haltaro = model_haltaro.predict(ave_data)
model_haltaro.plot_components(data_result_haltaro)
ここまでで、上記の記事 (1) の著者 haltaro さんとほぼ同じ処理をしました。ここからモデルの残差を求めます。
残差を求めるのは非常に簡単で、モデルの結果には予測値の yhat が、入力したデータには y があるはずなので、この差をとれば計算できます。今後何度も使うことになるので、関数として定義しておきます。
def add_residuals(data_input, data_result):
"""
data_input: Prohpet に入力したデータ
data_result: Prophet で predict したデータ
"""
data = data_result.copy()
data['y'] = data_input['y']
data['residual'] = data['y'] - data['yhat']
return(data)
data_result_haltaro = add_residual(ave_data, data_result_haltaro)
これで、 predict の結果に残差の列を追加したデータができました。
テクニック1: 残差ヒストグラム
この残差のヒストグラム描いてみましょう。
def plot_prophet_residual_histo(data, column='residual'):
"""
ヒストグラムを作成
data: 当てはめ結果データ
column: 残差の列名
"""
return ggplot(data,
aes(x='ds')
) + geom_histogram(aes(x=column), bins=50, fill='steelblue')
print(plot_prophet_residual_histo(data_result_haltaro, column='residual'))
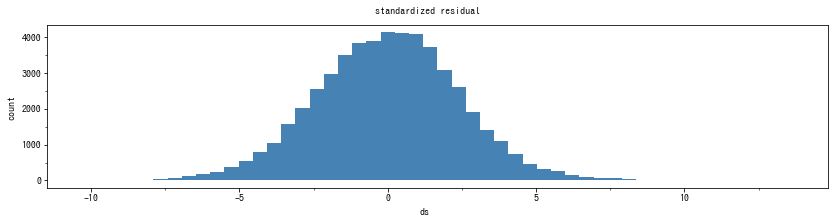
すると、以下のようなヒストグラムが得られるはずです。
回帰分析と同様に、ゼロを頂点とした左右対称な釣鐘型分布になっていれば、問題ありません。これは、時系列でないデータの回帰分析でもよく使われるやり方です2。しかし、時系列分析の場合は、残差のヒストグラムだけではわからないこともあります。そこで、次の残差プロットのテクニックが必要になります。
なお、もしも分布が上記のようにならない場合、変数を変換すると良いでしょう。よくあるパターンは、入力データの y を対数にすることです。その場合、対数変換後の値でモデルが作られるので、実際の予測値を見るときは指数変換する必要があります。
テクニック2: 残差プロット
残差ヒストグラムは時間の情報を削ったグラフです。時系列モデルなので、時間の関係を確認するのは大切です。そこで、次に、横軸を年月、縦軸を残差にしてプロットしてみます。
def plot_prophet_residual(data, column='residual'):
return ggplot(data,
aes(x='ds', y='residual')) + geom_line(color='steelblue')
print(plot_prophet_residual(data_result_haltaro))
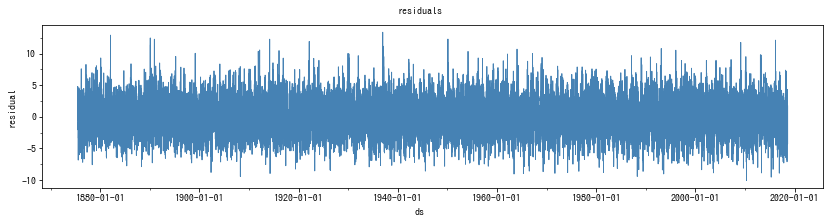
すると、ゼロを中心として上下に振れる折れ線グラフができました。
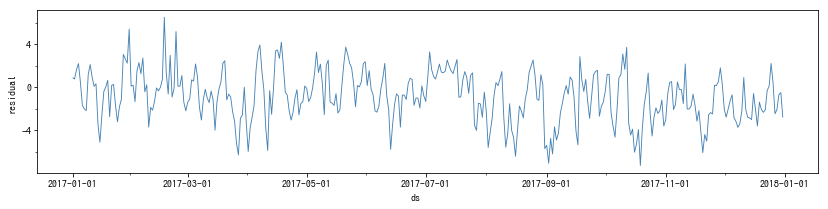
理論上、残差は平均がゼロ、分散が一定であると仮定しています。このグラフを見るかぎり、残差は全期間を通してゼロ周辺で変動し、振れ幅も同じに見えます。よって、問題はなさそうです。しかし、データの期間が長すぎると線で塗りつぶされて見づらいため、期間を分けて見てみましょう。2017年だけを取り出すと、以下のようになりました。
こうしてみると、やや動きに偏りがあるようにも見えます。残差がしばらくプラスの方向ばかりに触れてから戻ったり、逆にマイナス方向にとどまったりしている箇所があります。しかし、ノイズはあくまでランダムなので、偶然そうなっただけかもしれません。そこで、次に、残差の傾向を集約したグラフを作ってみます。
テクニック3: 残差コレログラム
時系列データの変数というのはしばしば、自身の過去の値に依存します。これを自己相関といいます。しかし、多くの統計モデルは、誤差が互いに相関しないことを暗黙のうちに前提としています。よって、残差に自己相関がないほうが時系列予測モデルとして適切ということになります。自己相関は、1つ前の値、2つ前の値、というふうに、ラグを広げることができます。ラグの広さ順に自己相関の大きさを棒グラフで表したものを、コレログラムといいます。以下では Prophet の結果から残差のコレログラムを作成しています。
def plot_prophet_autocorr(data, column='residual', max_lag=366):
"""
自己相関係数を計算してプロットする
"""
g = ggplot(pd.DataFrame([(
l,
data[column].autocorr(l)
) for l in range(max_lag)],
columns=['lag', 'autocorr']),
aes(x='lag', y='autocorr')
) + geom_bar(stat='identity', fill='steelblue')
return g + scale_x_continuous(
breaks=range(1, max_lag, 144)
) + labs(y=' ', title='residual autocorretaion')
print(plot_prophet_autocorr(data_result_haltaro,
max_lag=60) + scale_x_continuous(
breaks=range(0, 60, 10)))
print(plot_prophet_autocorr(data_result_haltaro,
max_lag=365 * 10) + scale_x_continuous(
breaks=list(range(0, 365*10, 365)))
)
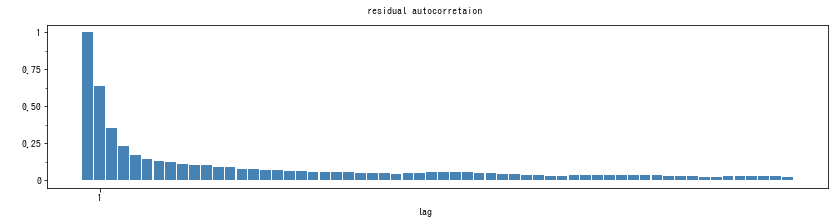
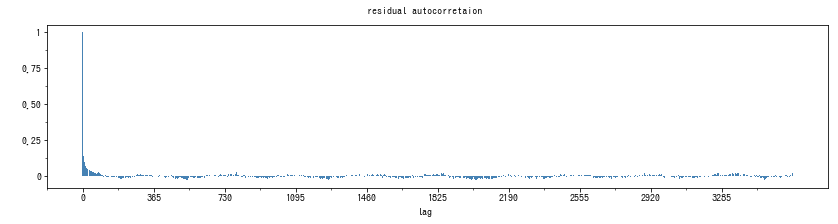
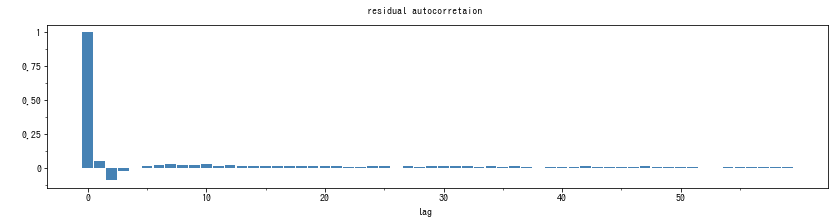
すると、以下のような結果が得られました。
というコレログラムが得られます。ラグがゼロのときは、自分自身との相関係数なので、どんなデータでも必ず1になります。自己相関がないものが好ましいということは、ラグ1以降の自己相関係数がゼロであると良い、ということです。ただし、実際にはノイズがあるので、必ずしも正確にゼロになるとは限りません。よって、ラグ1以降の自己相関がゼロの周辺で小さく上下するようなグラフが理想となります。今回のデータでは、たしかに自己相関は急激に減少していますが、ゼロ以下にならず、ずっと小さな値を維持しています。時系列モデルを改良するとしたら、このあたりに余地がありそうです。
なお、残差コレログラムの自己相関が大きい場合、残差プロットもそれに対応してもう少し変わってきます。自己相関が大きいということは、直前の値に強く依存するということで、振動が小刻みでなくなります。
また、一旦自己相関が減少するも、ラグが広がると再び自己相関があるような場合は、残差に周期性が残っていることになります。 Prophet は周期成分を取り出しますが、このような場合は何らかの取りこぼしがあるということです。ラグの大きさでだいたい周期の大きさがわかります。 Prophet のデフォルト設定で最も大きな周期成分は1年周期なので、今回はそれより長いラグについても見ておくといいかもしれません。以下が、およそ10年のラグを取った場合です。
どうやら、10年規模の大きな周期性は見当たらないようです。最大のラグ長は扱うデータしだいで変える必要があります。あまりラグを長くすると、ラグの大きな自己相関の計算に使えるサンプルサイズが小さくなるため、右端へ行くと精度が悪くなります。
テクニック4: 残差の累積プロット
残差をそのまま時系列に沿ってプロットするだけでなく、残差の累積値をプロットすることも有効です。ただし、残差はマイナスにも振れるので、そのまま足すのではなく、絶対値にしてから足していきます。
def plot_prophet_cum_abs_error(data, column='residual'):
"""
累積絶対和を計算してプロットする
"""
return ggplot(data.assign(cumsum=data[column].abs().cumsum()),
aes(x='ds', y='cumsum')
) + geom_line(
color='steelblue'
) + labs(title='cumulative abs. error')
print(plot_prophet_cum_abs_error(data_result_haltaro))
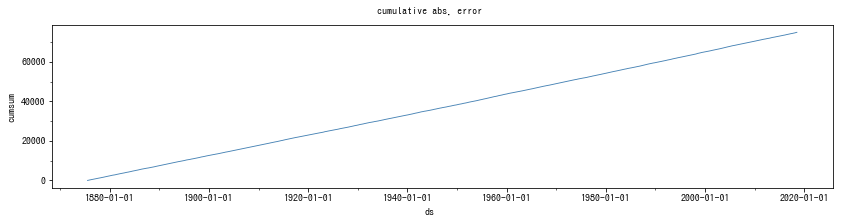
残差が理想的なら、累積値は時間経過に伴って直線的に増加していくはずです。もし、ある時点で急に累積値が増えたり、傾斜が変わってりしている場合、変化点が存在している可能性があります。変化点の設定を変えてみると良いでしょう。
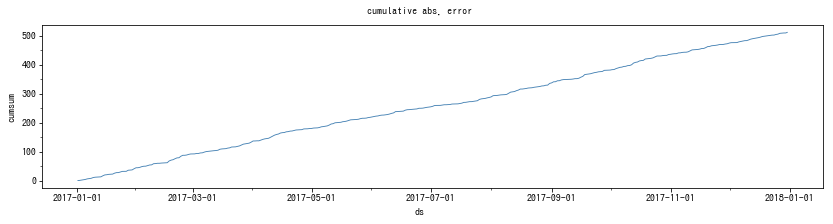
結果は以下の通りでした。全期間ではほぼ直線に見えるため、2017年だけを抜き出したものも掲載しました。
今回のデータとモデルは、整然とした直線に近いので、問題はなさそうです。
平均気温はどうやら、かなり規則的な変化をするようです。個人的な経験上、多くの時系列データでは、これよりだいぶ乱れたグラフができあがります。
モデルの当てはまりの良さを調べる
これは少し悩みました。
モデルの当てはまりの良さを数値化する指標として、残差の2乗の平均値である平均二乗誤差 (MSE) と、その平方根をとった RMSE、2乗の代わりに絶対値をとった平均絶対誤差 (MAE) があります。これらは広く使われていますが、複数モデルの比較に使える相対的な指標で、ある値以上/未満だからどうだ、という判断に使うことができません。
Prophet にはさらに、平均絶対パーセント誤差 (MAPE) という指標が使われています。 MAPE は誤差の大きさが元の時系列に対して何パーセントかで計算するため、元の時系列の単位やスケールに関係なく評価できる、という利点がありますが、一方で、
- 原系列に一つでもがゼロが含まれる場合は計算できない (無限大になってしまう)
- マイナス方向の誤差よりもプラス方向の誤差を評価する
という問題があります。 Prophet はもともとプラスの値しか取らないような KPI の時系列データの分析を想定しているので、 この限りでは MAPE でも問題はありませんが、気温データとは相性がかなり悪いです。
そこで、今回は、プラスマイナスの値を取る気温データに対して適切で、かつわかりやすい基準のある指標として、 平均絶対尺度誤差 (MASE; Mean Absolute Scaled Error) を使うことにします3。 MASE は、通常の MAE と、$y_{t}$ の予測値を実際の直前の値 $y_{t-1}$ とする「ナイーブな」 予測モデルの MAE との比です。MASE は、MAPE のような問題点がなく、かつ誤差が 1 未満かどうかで、そのモデルが直前の値を予測値に代用するような単純なモデルより優れているかどうかを判定できます。
ただし、 MASE をひたすら小さくすればいいわけではありません。そのような場合はたいてい過剰適合が発生し、未来のデータに対する精度が低下します。そのため、普通はデータを当てはめ (学習) 用と検証用に分けて交差検証 (CV) をしながらモデルを決めるのですが、今回焦点となっているのは、ここ最近20年の傾向なので、CVすることができません4。
Prophet における CV の詳しい話は、以下を参考にしてください。
モデルの改良
haltaro さんと HotAllure さんのモデルの MASE を計算すると、それぞれ 1.2305, 1.2298 でした。
以上の残差診断の結果を踏まえると、今回の気温モデルは、気温の長期的な変化をだいたいうまく近似できていますが、精度はさほどよくありません。残差診断の結果では、残差の自己相関が残存しているのが気になります。これをうまく解消できれば、結果が変わってくるかもしれません。
自己相関が残存している時系列は、自己回帰成分か、確率トレンド成分が存在すると予想できます。
自己回帰成分の場合、ある程度ラグが長くなれば自己相関が消えますが、確率トレンドを持つ場合、長期に渡って自己相関が残ります。ランダムウォークと呼ばれるタイプの時系列モデルは、確率トレンドのある典型例です。
しかし、 Prophet は確率トレンドのある時系列への対処が難しいので、今回は自己回帰項を追加しました5。自己回帰項とは、時系列の1つ前の変数で回帰する、ということです。今回の場合、Prophet
のモデルは以下のようになります。
$$\begin{aligned}y(t)= & g(t)+s(t)+\phi y_{t-1}+\epsilon_{t}\end{aligned}$$
この自己回帰を、 Prophet の「外部変数による回帰」という機能を使って再現します。つまり、入力データに新たに $y_{t-1}$を別の列として追加します。 Prophet の入力データは Pandas のデータフレームオブジェクトなので、 shift() メソッドを使えばこの列は簡単に作成できます6。
結果として、 MASE が 0.9210 となり、いちおうナイーブ予測よりもうまく予測できているモデルということになりました。コレログラムは以下のようになりました。
Hotallure さんの、1年毎に変化点を設けるモデルでも、コレログラムに同様の傾向があったため、自己回帰を追加しましたが、90年代後半からトレンドが低下しているという結果は変わりませんでした。
なお、この他にも、 Prophet のデフォルト設定では最大でも1年周期の成分しか追加しないことから、10年周期の周期成分を追加してみましたが、結果に大きな違いがなかったため省略します。どうやら平均気温は、外部要因の影響が強いのかもしれません7。
「夏暑く冬寒い仮説」への答えは
「ここ数年は暑いのに、モデルでは減少トレンドにある」という問題意識から、 HotAllure さんが考えた最高気温と最低気温を使うというアイディアは面白いですが、最高気温と最低気温は1日ごとの値であるという点が気になります。おそらく日々の最高気温は真昼ごろの気温で、最低気温は明け方直前くらいの気温になるはずです。すると、最高気温・最低気温への当てはめは、正確には日中気温の推移と夜間の気温の推移を見ていることになり、正確には (本人が指摘しているように) 夏・冬の比較になっていません。
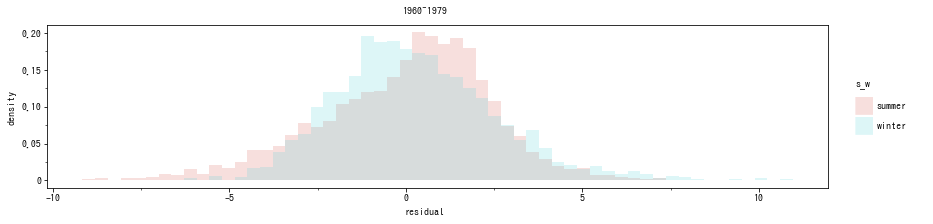
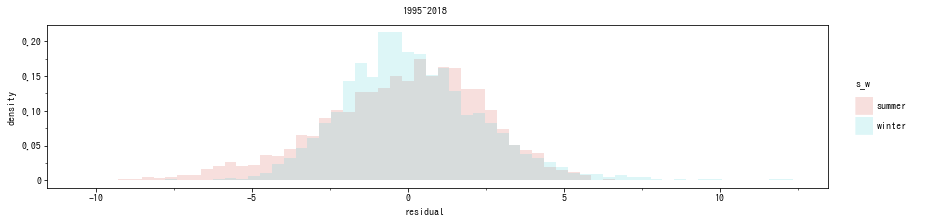
ここまでで説明した残差診断の応用で、データを夏と冬に分割して残差を比べてみましょう。仮説が正しいなら、夏のデータは残差がプラス方向に偏り、冬のデータは残差がマイナス方向に偏りがちになる、という傾向が1990年代後半から顕著に見られるようになるはずです。
夏・冬に分けて残差ヒストグラム作成をします。夏は 6, 7, 8 月、冬は 12, 1, 2月とします。さらに、1995~2018年までのものと、経時的な変化を見るため、 1960, 70年代のデータを取り出して同様のヒストグラムを作成しました。その結果、以下のようになりました8。
夏は残差がプラス方向に偏り、冬は逆にマイナス方向に偏っていますが、この傾向は両方の年代で見られます。よって、最近の平均気温のトレンドの停滞の原因は、「夏暑く冬寒い」ではないようです。一方で、最高気温・最低気温は近年それぞれ上昇・下降トレンドとなっています。つまり、ここ最近は、夏暑く冬寒くなっているのではなく、1日の気温差が大きくなっている、ということになります。
ただし、これはあくまで日毎の気温データのみから言えることです。実際には気温は様々な要因の影響を受けていると考えられ、外部要因を考慮して分析し直したらやはり「夏暑く冬寒い仮説」が正しかった、となることも十分考えられます。
以下は今回使用したソースコードの全体です (あまり整頓されていませんがご容赦ください。あくまで書き方の参考としてください。)
ソースコードが長いため折りたたんでいます
# ! /usr/bin/env python
# -*- coding: utf-8 -*-
# Python
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mizani.breaks import date_breaks
from mizani.formatters import date_format
from plotnine import ggplot, aes, theme, labs
from plotnine.geoms import *
from plotnine.scales import *
from plotnine.facets import *
from plotnine.stats import *
from plotnine.themes import *
from plotnine.coords import *
import plotnine
from fbprophet import Prophet
from fbprophet.diagnostics import cross_validation
from fbprophet.diagnostics import performance_metrics
from fbprophet.plot import plot_cross_validation_metric
plotnine.options.current_theme = theme(
figure_size=(14, 3),
text=element_text(family='IPAGothic')
)
data_dir = Path().cwd() / 'data'
def add_residuals(data_input, data_result):
data = data_result.copy()
data.set_index('ds', drop=False, inplace=True)
data['y'] = data_input.set_index('ds')['y']
data['residual'] = data['y'] - data['yhat']
return(data)
def MAE(data):
return (data['y'] - data['yhat']).abs().dropna().mean()
def MAPE(data):
data = data.copy()
data = data[['y', 'yhat']].dropna(how='all')
return ((data['yhat'] - data['y']).abs() / data['y']).dropna().mean()
def MASE(data):
return MAE(data) / data['y'].diff().abs().dropna().mean()
# 診断用の関数
def plot_prophet_residual(data, column='residual'):
return ggplot(data,
aes(x='ds', y='residual')) + geom_line(color='steelblue')
def plot_prophet_residual_histo(data, column='residual'):
"""
ヒストグラムを作成
"""
return ggplot(data,
aes(x='ds')
) + geom_histogram(aes(x=column), bins=50, fill='steelblue')
def plot_prophet_residual_qq(data, column='residual'):
"""
残差で正規q-qプロットする
"""
return ggplot(data,
aes(sample=column)
) + stat_qq(color='steelblue') + stat_qq_line(
color='steelblue') + theme(aspect_ratio=1.0)
def plot_prophet_autocorr(data, column='residual', max_lag=366):
"""
自己相関係数を計算してプロットする
"""
g = ggplot(pd.DataFrame([(
l,
data[column].autocorr(l)
) for l in range(max_lag)],
columns=['lag', 'autocorr']),
aes(x='lag', y='autocorr')
) + geom_bar(stat='identity', fill='steelblue')
return g + scale_x_continuous(
breaks=range(1, max_lag, 144)
) + labs(y=' ', title='residual autocorretaion')
def plot_prophet_cum_abs_error(data, column='residual'):
"""
累積絶対和を計算してプロットする
"""
return ggplot(data.assign(cumsum=data[column].abs().cumsum()),
aes(x='ds', y='cumsum')
) + geom_line(
color='steelblue'
) + labs(title='cumulative abs. error')
def plot_prophet_summary(data):
print(plot_prophet_residual_histo(data) + labs(
title=' standardized residual')
)
print(plot_prophet_autocorr(data))
print(ggplot(data,
aes(x='ds', y='residual')
) + geom_line(
color='steelblue'
) + labs(title='residuals')
)
print(plot_prophet_cum_abs_error(data))
all_data = pd.concat(
[pd.read_csv(
file,
encoding='cp932',
skiprows=6,
header=None,
names=['date', 'average', 'high', 'low'],
usecols=[0, 1, 4, 7],
) for file in (data_dir / 'raw').glob('data_*.csv')]
)
all_data['date'] = pd.to_datetime(all_data['date'])
# 最初の数年は欠損なので削除
all_data = all_data.set_index('date', drop=False)['1875-06-10':'2018-08-01']
# Prophet用DataFrameを生成
ave_data = all_data[['date', 'average']].rename(
columns={'date': 'ds', 'average': 'y'})
data_rain = pd.concat(
[pd.read_csv(
file,
encoding='cp932',
skiprows=5,
header=None,
names=['date', 'rain'],
usecols=[0, 1],
) for file in (data_dir / 'raw').glob('rain_*.csv')]
)
data_rain['date'] = pd.to_datetime(data_rain['date'])
data_rain = data_rain.set_index('date', drop=False)['1875-06-10':'2018-08-01']
data_rain.info()
data_rain['rain'].fillna(0, inplace=True)
ggplot(all_data, aes(x='date', y='average')) + geom_line(color='steelblue')
ggplot(data_rain, aes(x='date', y='rain')) + geom_line(color='steelblue')
# ----- modeling ------
# the model by haltaro
model_haltaro = Prophet(weekly_seasonality=False)
model_haltaro.fit(ave_data)
data_result_haltaro = model_haltaro.predict(ave_data).set_index('ds',
drop=False)
data_result_haltaro = add_residuals(ave_data, data_result_haltaro)
print('MAE: %.4f' % MAE(data_result_haltaro))
print('MASE: %.4f' % MASE(data_result_haltaro))
model_haltaro.plot_components(data_result_haltaro)
print(plot_prophet_residual_histo(data_result_haltaro))
print(plot_prophet_residual_qq(data_result_haltaro))
print(plot_prophet_residual(data_result_haltaro))
print(plot_prophet_residual(data_result_haltaro['2017-01-01':'2017-12-31']))
print(plot_prophet_autocorr(data_result_haltaro,
max_lag=60) + scale_x_continuous(
breaks=range(0, 60, 10)))
print(plot_prophet_autocorr(data_result_haltaro, max_lag=366))
print(plot_prophet_autocorr(data_result_haltaro,
max_lag=365 * 10) + scale_x_continuous(
breaks=list(range(0, 365*10, 365)))
)
print(plot_prophet_cum_abs_error(data_result_haltaro))
cv_haltaro = cross_validation(model_haltaro,
initial=int(50 * 365),
period=int(20 * 365.25),
horizon=int(20 * 365.25)
)
plot_cross_validation_metric(performance_metrics(cv_haltaro), metric='mape')
# the model by HotAllure
model_HotAllure = Prophet(weekly_seasonality=False,
n_changepoints=142,
changepoint_range=1.0)
model_HotAllure.fit(ave_data)
data_result_HotAllure = model_HotAllure.predict(ave_data).set_index('ds', drop=False)
data_result_HotAllure = add_residuals(ave_data, data_result_HotAllure)
print('MAE: %.4f' % MAE(data_result_HotAllure))
print('MASE: %.4f' % MASE(data_result_HotAllure))
model_HotAllure.plot_components(data_result_HotAllure)
print(plot_prophet_residual_histo(data_result_HotAllure))
print(plot_prophet_residual(data_result_HotAllure))
print(plot_prophet_residual(data_result_HotAllure['2017-01-01':'2017-12-31']))
print(plot_prophet_autocorr(data_result_HotAllure,
max_lag=60) + scale_x_continuous(
breaks=range(0, 60, 10)))
print(plot_prophet_autocorr(data_result_HotAllure, max_lag=366))
print(plot_prophet_autocorr(data_result_HotAllure,
max_lag=365 * 10) + scale_x_continuous(
breaks=list(range(0, 365*10, 365)))
)
print(plot_prophet_cum_abs_error(data_result_HotAllure))
# My idear:
ave_data_inplemented = ave_data.copy()
ave_data_inplemented['y_origin'] = ave_data_inplemented['y']
ave_data_inplemented['y'].interpolate(inplace=True)
ave_data_inplemented['y_lag'] = ave_data_inplemented['y'].shift()
ave_data_inplemented = ave_data_inplemented.iloc[1:, ]
model_ar = Prophet(weekly_seasonality=False, yearly_seasonality=30,
daily_seasonality=False,
n_changepoints=5,
)
model_ar.add_regressor('y_lag')
model_ar.fit(ave_data_inplemented)
data_result_ar = model_ar.predict(
ave_data_inplemented).set_index('ds', drop=False)
data_result_ar = add_residuals(ave_data_inplemented, data_result_ar)
print('MAE: %.4f' % MAE(data_result_ar))
print('MASE: %.4f' % MASE(data_result_ar)) # lag: .9210
model_ar.plot_components(data_result_ar)
print(plot_prophet_residual_histo(data_result_ar))
print(plot_prophet_residual_qq(data_result_ar))
print(plot_prophet_residual(data_result_ar))
print(plot_prophet_residual(data_result_ar['2017-01-01':'2017-12-31']))
print(plot_prophet_autocorr(data_result_ar,
max_lag=60) + scale_x_continuous(
breaks=range(0, 60, 10)))
print(plot_prophet_autocorr(data_result_ar, max_lag=366))
print(plot_prophet_autocorr(data_result_ar['1970-01-01':], max_lag=366))
print(plot_prophet_autocorr(data_result_ar,
max_lag=365 * 10) + scale_x_continuous(
breaks=list(range(0, 365*10, 365))
) + coord_cartesian(ylim=[0, .1])
)
print(plot_prophet_cum_abs_error(data_result_ar))
print(plot_prophet_cum_abs_error(data_result_ar['2017-01-01':'2017-12-31']))
# 夏・冬に分けて残差ヒストグラム作成
data_result_ar['summer'] = data_result_ar['ds'].dt.month.isin(range(6, 9))
data_result_ar['winter'] = data_result_ar['ds'].dt.month.isin([12, 1, 2])
data_result_ar['s_w'] = ''
data_result_ar['s_w'].mask(data_result_ar['summer'], 'summer', inplace=True)
data_result_ar['s_w'].mask(data_result_ar['winter'], 'winter', inplace=True)
ggplot(data_result_ar['1960-01-01':'1980-01-01'].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2)
ggplot(data_result_ar['1995-01-01':].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2)
data_result_HotAllure['summer'] = data_result_HotAllure['ds'].dt.month.isin(range(6, 9))
data_result_HotAllure['winter'] = data_result_HotAllure['ds'].dt.month.isin([12, 1, 2])
data_result_HotAllure['s_w'] = ''
data_result_HotAllure['s_w'].mask(data_result_HotAllure['summer'], 'summer', inplace=True)
data_result_HotAllure['s_w'].mask(data_result_HotAllure['winter'], 'winter', inplace=True)
ggplot(data_result_HotAllure['1960-01-01':'1980-01-01'].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1960~1979')
ggplot(data_result_HotAllure['2000-01-01':].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1995~2018')
# model of max temperature
data_high= all_data[['date', 'high']].rename(
columns={'date': 'ds', 'high': 'y'})
data_high['y'].interpolate(inplace=True)
data_high['y_lag'] = data_high['y'].shift()
model_high = Prophet(weekly_seasonality=False,
n_changepoints=142,
changepoint_range=1.0)
model_high.add_regressor('y_lag')
model_high.fit(data_high)
data_result_high = model_high.predict(data_high).set_index('ds', drop=False)
data_result_high = add_residuals(data_high, data_result_high)
model_high.plot_components(data_result_high)
data_result_high['summer'] = data_result_high['ds'].dt.month.isin(range(6, 9))
data_result_high['winter'] = data_result_high['ds'].dt.month.isin([12, 1, 2])
data_result_high['s_w'] = ''
data_result_high['s_w'].mask(data_result_high['summer'], 'summer', inplace=True)
data_result_high['s_w'].mask(data_result_high['winter'], 'winter', inplace=True)
ggplot(data_result_high['1960-01-01':'1980-01-01'].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1960~1979')
ggplot(data_result_high['2000-01-01':].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1995~2018')
# model of min temperature
data_low= all_data[['date', 'low']].rename(
columns={'date': 'ds', 'low': 'y'})
data_low['y'].interpolate(inplace=True)
data_low['y_lag'] = data_low['y'].shift()
model_low = Prophet(weekly_seasonality=False,
n_changepoints=142,
changepoint_range=1.0)
model_low.add_regressor('y_lag')
model_low.fit(data_low)
data_result_low = model_low.predict(data_low).set_index('ds', drop=False)
data_result_low = add_residuals(data_low, data_result_low)
model_low.plot_components(data_result_low)
data_result_low['summer'] = data_result_low['ds'].dt.month.isin(range(6, 9))
data_result_low['winter'] = data_result_low['ds'].dt.month.isin([12, 1, 2])
data_result_low['s_w'] = ''
data_result_low['s_w'].mask(data_result_low['summer'], 'summer', inplace=True)
data_result_low['s_w'].mask(data_result_low['winter'], 'winter', inplace=True)
ggplot(data_result_low['1960-01-01':'1980-01-01'].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1960~1979')
ggplot(data_result_low['2000-01-01':].query('s_w != ""'),
aes(x='residual', y='..density..', group='s_w', fill='s_w')
) + geom_histogram(position='identity', alpha=.2) + labs(title='1995~2018')
# rain regression
data = pd.concat([all_data[['date', 'average']],
data_rain.drop(columns=['date'])], axis=1).rename(
columns={'average': 'y', 'date': 'ds'})
data['y'].interpolate(inplace=True)
data['y_lag'] = data['y'].shift()
data['rain_lag'] = data['rain'].shift()
data = data.iloc[1:, :]
model_rain = Prophet(weekly_seasonality=False,
daily_seasonality=False,
n_changepoints=5,
)
# model_rain.add_regressor('y_lag')
model_rain.add_regressor('rain_lag')
model_rain.fit(data)
data_result_rain = model_rain.predict(data)
data_result_rain = add_residuals(data, data_result_rain)
print('MAE: %.4f' % MAE(data_result_rain))
print('MASE: %.4f' % MASE(data_result_rain))
model_rain.plot_components(data_result_rain)
plot_prophet_residual_histo(data_result_rain)
plot_prophet_residual(data_result_rain)
plot_prophet_autocorr(data_result_rain, max_lag=100)
参考文献
私が今までに読んだ本や、経験を元に内容を構成したので、これといったものはないのですが、以下の本が比較的近いです。モデルを作る前に時系列の特徴を見る方法として、コレログラムを提示しています。ただし、 Prophet をベースにした本ではないので、取り扱っている時系列モデルの種類が違います9。
- 沖本竜義『経済・ファイナンスデータの計量時系列分析』は ARIMA や GARCH モデルが主で、金融関係のデータを取り扱うことを前提としています。
- 北川源四郎『時系列解析入門』は SARIMA や状態空間モデルの言及が多くよりテクニカルです。いずれも、様々な時系列データのコレログラムがどういう傾向を示すのかについて言及されています。
-
Prophetにはなぜか、残差を計算する機能がありません。簡単さを求めた結果なのかもしれませんが、モデル改良の勘所は残差にあるので、少し不親切な気がします。 ↩ -
また、残差のヒストグラムの代わりに、 q-q プロットを描画する、という方法も考えられます。こちらのほうが、理論上の分布とどれくらい離れているかがより明確にわかります。 ↩
-
MASE について日本語で詳しく説明している文献は残念ながらありません。 MASE が最初に提案された論文として、 Hyndman, R. J. and Koehler A. B. (2006). "Another look at measures of forecast accuracy." International Journal of Forecasting volume 22 issue 4, pp. 679-688. doi:10.1016/j.ijforecast.2006.03.001 があります。 Wikipedia 英語版にも記事があります。 ↩
-
よって、ここでの議論は、過剰適合が発生していないことが前提になっています。 ↩
-
とはいえ、日々の気温がランダムウォーク的に変化するとも考えにくいので、そこまで問題があるとも思いません。 ↩
-
ただし、今回のデータはところどころに欠損があります。ラグを取ると欠損のある行が倍増するため、ラグ変数列を作る前に、$y_{t}$ の欠損値を前後の平均値で補間しておきます。 ↩
-
弊社弊チームきっての気象予報士に聞いたところ、気温は風向風速や上空の気温などの影響を受けやすいようです。 ↩
-
夏季・冬季の分け方を多少変更して確認しましたが、ヒストグラムに見られる傾向は変わりませんでした。 ↩
-
Prophet のモデルも ARIMA も「状態空間モデル」と呼ばれるグループの一形態なので, 数学的には同じカテゴリですが, それぞれ表現の自由度が違います. ↩