概要
Factorization Machine (FM) の性質についての確認と, 最近の研究動向の調査についてのまとめです. 以下について言及しています
- FMの特徴を従来の線形モデルなどと対比して説明
- 現在使用可能なFMの実装と, それぞれの長所短所を紹介
- 最新の研究動向についてもいくつかピックアップ
FM の特徴
Rendle (2010)はサポートベクターマシン (SVM) などスパースなデータの学習に失敗する従来のアルゴリズムに対する代案としてFactorization Machine (FM, 分解器) を提案した. スパースなデータは, 例えばカテゴリカル変数, bag-of-word だったり, リコメンドシステムなどでよくありうる. 基本的なSVMは超分離平面で線形分離できるような分類タスクのみ良好なパフォーマンスを発揮し, 非常にスパースなデータではカーネル空間をうまく学習できないことが多い一方で, 従来スパースデータの学習に向いているとされていたテンソル分解モデル (tensor factorization model) は入力データに制約があった. 彼の提案するFMは名前の通りパラメータの行列を因数分解して表現するモデルで, そういう意味では特異値分解 (SVD) や主成分分析 (PCA) などと似ている. しかし, FM は以上に挙げた従来のモデルの問題を解決し, 以下のような長所をアピールしている.
SVMなど既存の方法ではうまくいかないような, 非常にスパースなデータでも学習できる
時間計算量のオーダーが線型であり, 大きなデータにも応用しやすい
従来のfactorization modelと違い, データの形式に制約がない
なお, 今回は推薦システムではなく分類タスクへの応用を念頭に置いて解説する.
従来の多項式モデル
一番簡単なFMのモデルは2つの特徴量の交差項に対する相互効果を考慮する, 2元FM (2-way FM) である. これを従来の線形モデルとの違いで比較していく. なお, ここでの説明はJuan, Zhung, and Chin (2015) のスライドとほぼ同じである.
$\boldsymbol{x}$ を特徴行列から取り出した $D$次元の特徴ベクトルとする. FMはスパースデータを考慮しているので, カテゴリカル変数をone-hot encodingで変換して次元が大きくなった状態を想像してほしい. $\boldsymbol{x}$と正解ラベル$y$のペアのインスタンス $(\boldsymbol{x}^{(n)},y^{(n)})$ を考える. 従来的な線型モデルだと, $\boldsymbol{x}$と同じ長さのパラメータベクトル $\boldsymbol{w}\in\mathbb{R}^{D}$との内積で以下のように表現したモデルを学習させる.
$$
\begin{aligned}
\phi(\boldsymbol{x},\boldsymbol{w}):= & \left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle =\sum_{i=1}^{D}w_{i}x_{i}\end{aligned} \tag{1}
$$
ここで $\left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle$ とは$\boldsymbol{w},\boldsymbol{x}$ の内積を表す. 従来のやり方では線型モデルに相互作用項を追加するには以下のように2次多項式項を追加する.
$$
\begin{aligned}
\phi_{\mathit{poly2}}(\boldsymbol{x},\boldsymbol{w}):= & \left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle +\sum_{(i,j)\in C}w_{i,j}x_{i}x_{j}\end{aligned}
\tag{2}
$$
$C$ は, $\{1,\cdots,D\}$ までの $D$ 個の要素の組み合わせ全体を表す集合である. つまり, 2つの特徴 $x_{j},x_{k}$ の積 $x_{j}x_{k}$ が$D(D-1)$ 通りあり, それぞれに対してパラメータ $w_{j,k}$ を用意していることになる. ただし $D$ の大きさ次第では計算困難になるので, 実際には組み合わせ $C$ の一部だけを使う場合が多いだろう. しかし, どれを使うかの取捨選択にはやはりコストがかかる. そして, 特にデータのほとんどがカテゴリカル変数で, これらをone-hot encodingしている想定では, $D$ が非常に大きくなることが予想される.
FM の利点
一方でFMはRendle によって以下のように定義されている.
$$
\begin{aligned}
\phi_{\mathit{FM2}}(\boldsymbol{x},\boldsymbol{w}):= & w_0 + \left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle +\sum_{i=1}^{D}\sum_{j=i+1}^{D}\left\langle \boldsymbol{v}_{i},\boldsymbol{v}_{j}\right\rangle x_{j}x_{j}\nonumber \\
= & w_0 + \left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle +\sum_{(i, j)\in C}\left\langle \boldsymbol{v}_{i},\boldsymbol{v}_{j}\right\rangle x_{j}x_{j}\end{aligned}\tag{3}
$$
$\boldsymbol{v}\_{i},\boldsymbol{v}\_{j}$ は長さ $k$ のベクトルで, 関連研究では潜在ベクトル (latent vector) と呼ばれることが多い. 長さ $k$ は任意に決められるハイパーパラメータである.
多項式モデルとFMがどう違うのか比較してみる. $\hat{w}_{i,j}=\left\langle \boldsymbol{v}_{i},\boldsymbol{v}_{j}\right\rangle$ を$i,j$成分とするパラメータ行列を $\mathbf{W}$ で表すと, これに対応する FM のパラメータは, $\mathbf{V}\mathbf{V}^{\top}$ である ($\mathbf{W}$ が正定値行列という前提). $\mathbf{V}$ は $\boldsymbol{v}_{1}\cdots\boldsymbol{v}_{D}$ を積み上げた行列のことである. これを$\mathbf{W}$の近似という意味で, 以降は$\hat{\mathbf{W}}$と表す.
$$
\begin{aligned}
\mathbf{V}:= & \begin{bmatrix}\boldsymbol{v}_{1}^{\top}\\
\vdots\\
\boldsymbol{v}_{D}^{\top}
\end{bmatrix},\\
\hat{\mathbf{W}}=\mathbf{V}\mathbf{V}^{\top}= & \begin{bmatrix}\boldsymbol{v}_{1}^{\top}\\
\vdots\\
\boldsymbol{v}_{D}^{\top}
\end{bmatrix}\begin{bmatrix}\boldsymbol{v}_{1} & \cdots & \boldsymbol{v}_{D}\end{bmatrix}\\
= & \begin{bmatrix}\boldsymbol{v}_{1}^{\top}\boldsymbol{v}_{1} & \cdots & \boldsymbol{v}_{1}^{\top}\boldsymbol{v}_{D}\\
\vdots & \ddots & \vdots\\
\boldsymbol{v}_{D}^{\top}\boldsymbol{v}_{1} & \cdots & \boldsymbol{v}_{D}^{\top}\boldsymbol{v}_{D}
\end{bmatrix}\\
= & \begin{bmatrix}\left\langle \boldsymbol{v}_{1},\boldsymbol{v}_{1}\right\rangle & \cdots & \left\langle \boldsymbol{v}_{1},\boldsymbol{v}_{D}\right\rangle \\
\vdots & \ddots & \vdots\\
\left\langle \boldsymbol{v}_{D},\boldsymbol{v}_{1}\right\rangle & \cdots & \left\langle \boldsymbol{v}_{D},\boldsymbol{v}_{D}\right\rangle
\end{bmatrix}\end{aligned}
$$
推薦システムへの応用では, ユーザー属性・商品属性という2軸でのデータを行列の因数分解 (matrix factorization) をする, と説明される事が多い1. FM も2つの特徴の相互作用効果を分解するという点でこのアイディアを受け継いでいるといえる.
Rendle (2010) は FM の利点を3つ挙げている.
1つは, $\mathbf{W}\simeq\hat{\mathbf{W}}$となる程度に $k$ の大きさを調整できるということである. FMを使わずに多項式モデルで相互作用をすべて表現しようとすれば, $D(D-1)/2$ 個のパラメータが必要になる. しかしFMでは, 例えば $k=1$ とすれば, FM の相互作用の係数が $v_{i}v_{j}$ で表現され, パラメータの数も $D(D-1)/2$ から $D$ 個に減り多項モデルよりも単純になる. 一般にFM ではパラメータ数が $Dk$ 個となり, $k$ を調整して $\mathbf{W}$より小さな行列 $\mathbf{V}$ だけを使って相互作用を表現可能である. $k$ を調整することで計算量を減らせるということである (最適な $k$ の大きさはデータに依存するが, 少なくとも $D$ より大きくする意味はないはず).
2つ目は, スパースなデータへの強みである. 従来の多項式モデルでは, $w_{i,j}x_{i}x_{j}$ というふうに組み合わせごとに個別に交互作用パラメータを用意して学習する必要があった. しかしスパースなデータではほとんどの$x_{i}, x_{j}$ がゼロになり, さらにその積となるとゼロでない成分はいっそう少なくなるので実際にはほとんど計算できない. しかしFMでは $x_{i}x_{j}$ の交互作用の大きさを $\left\langle \boldsymbol{v}\_{i},\boldsymbol{v}\_{j}\right\rangle$ , つまり, $x\_{i},x\_{j}$ それぞれに固有なベクトルの内積で表現している. よって, 相互作用成分の片方/両方がゼロでもどこかで非ゼロな $x\_{i},x\_{j}$ が現れていればパラメータ $\boldsymbol{v}\_{i},\boldsymbol{v}\_{j}$ を学習できる. これはFMが目的の相互作用成分のないデータからも交互作用効果を間接的に学習できることを意味する. Rendle (2010) では, 極端にスパースなデータでもうまく学習できたという実験結果を見せている.
3つ目が, 計算の容易さである. 単純に考えるとFM の相互作用項部分の計算時間は $O(kD^{2})$ になるが, 工夫することで線形時間 $O(kD)$ で計算できる. なぜなら以下のように変形できるため.
$$
\begin{aligned}
\sum_{i,j}\left\langle \boldsymbol{v}_{i},\boldsymbol{v}_{j}\right\rangle x_{i}x_{j}= & \frac{1}{2}\sum_{f=1}^{k}\left(\left(\sum_{i=1}^{D}v_{i,f}x_{i}\right)^{2}-\sum_{i=1}^{D}v_{i,f}^{2}x_{i}^{2}\right)\end{aligned}
$$
なお, 2次多項式モデルの場合は, $O(D^{2})$ である2.
M-way FM
ここまで, 2つの値の交差項だけを考慮した 2元 FM で説明したが, 3つ以上特徴量の交差項についても拡張できる. 2-way FM が行列因数分解 (matrix factorization) に対応しているなら, 3元以上の FM は, その拡張であるテンソル因数分解 (tensor factorization) に対応していると言える. この場合は以下のように表現できる.
$$ \begin{aligned} \phi\_{\mathit{FM}m}(\boldsymbol{x},\boldsymbol{w}):=\left\langle \boldsymbol{w},\boldsymbol{x}\right\rangle & +\sum_{C\in D^{M}}\left[\left[\prod\_{j\in C}x\_{j}\right]\sum\_{i=1}^{k}\left(\prod\_{j\in C}(\boldsymbol{v}_{j})\_{i}\right)\right]\end{aligned} $$ここで, $D^{M}$ は $M$ 個の $D$ の直積集合である. ただし, 3元以上の複雑なFMはあまり使われることがない.
具体的な学習方法
Rendle (2010) は, 学習した $\phi_{\mathit{FM2}}(\boldsymbol{x},\boldsymbol{w})$ は回帰, 2値分類, ランキング予測に使えるとしている. 例えば分類タスクならば, ロジスティック損失を最適化問題を解くことになる. いずれのタスクでも, 正則化を追加するのが良いとしている. この損失関数は従来どおり SGD で学習できる. 最適化計算のオーダーは $O(kD)$ から $O(km(\boldsymbol{x}))$の範囲となる. $m(\boldsymbol{x})$ は, $\boldsymbol{x}$の非ゼロ要素の数である.
発展版: Field-aware FM
追記: http://hhok777.hatenablog.com/entry/2016/10/19/204037 ここでも FMから順を追って FF
M を解説していた.
FM の発展版, フィールド認識型分解機 (Field-aware FM; FFM) は Jahrer et al. (2012) で最初に提案された3. ただし当初は, Rendle and Schmidt-Thieme (2010) によるペアワイズ相互作用テンソル因数分解 (PITF) の一般化として, Factor Model と呼ばれていた. FM の発展版として位置づけられ FFM と呼ばれるようになったのは Juan et al. (2016; Juan, Lefortier, and Chapelle (2017) 以降のようだ. 特に Juan et al. (2016) は FFM は FM の発展型であり, 行列因数分解 (MF) と紛らわしいが別物であると強調している.
FFM のモチベーションはこうである. FM ではカテゴリカル変数を one-hot encoding して特徴量とするのが前提であった. このため, 媒体, 広告主, 性別といった異なる属性情報がすべて一律 0/1 の値にされてしまった. 各特徴量が元はどのようなカテゴリカル変数のものだったかという情報が抜け落ちていることになる. FFM へ拡張したことで, このように, フィールドごとに特有の要因のある相互作用を表現できる.
具体的なモデルについて説明する. FM では 1つの特徴量ごとに 1つのベクトルパラメータ $\boldsymbol{v}$ が存在したが, FFM では1対1ではなく複数のベクトルパラメータを持つことができる. つまり, FM では, $x_{i}$, $x_{j}$ の相互効果の大きさを $\left\langle \boldsymbol{v}_{i},\boldsymbol{v}_{j}\right\rangle$ としていたが, FFM では $i$ と $j$ に対する相互作用ではなく, 以下の式になる.
$$
\begin{aligned}
\phi_{\mathit{FFM}}(\boldsymbol{w},\boldsymbol{x})=& \sum_{i,j}\left\langle \boldsymbol{v}_{i,f_{2}},\boldsymbol{v}_{j,f_{1}}\right\rangle x_{i}x_{j}
\end{aligned}
$$
| ラベル | フィールド | ||
|---|---|---|---|
| クリック | 媒体 (Publisher) | 広告主 (Adevertiser) | 性別 (Genger) |
| Yes | ESPN | Nike | 男 |
| No | ESPN | Nike | 女 |
| No | Vogue | Gucci | 男 |
| ラベル | 媒体 (P) | 広告主 (A) | 性別 (G) | |||
|---|---|---|---|---|---|---|
| クリック | 媒体 - ESPN | 媒体 - Vogue | 広告主 - Nike | 広告主 - Gucci | 性別 - 男 | 性別 - 女 |
| Y | 1 | 0 | 1 | 0 | 1 | 0 |
| N | 1 | 0 | 1 | 0 | 0 | 1 |
| N | 0 | 1 | 0 | 1 | 1 | 0 |
FM では, 変換後の各列 (=特徴量) ごとにベクトル $\boldsymbol{v}$ を1つだけパラメータとして持っているとしていた. しかし, FFM では, 他の列 (=フィールド) ごとにパラメータを持つ. 例えば表 1 の場合なら, 「媒体 - ESPN」 の特徴量は, 広告主 (A) と, 性別 (G) に対応するパラメータベクトルを持つ必要がある. よって, $\{\boldsymbol{v}_{e,A},\boldsymbol{v}_{e,G}\}$ の2つになる. よって, フィールド数を $F$ とすると, パラメータの数は $Dk$ から $DFk$ になる. 表 1 の例で全ての組み合わせを書くと, 表 2 のようになる. そのぶん FM と比べてパラメータが増えているから, オーダーは $O(\bar{D}^{2}k)$ へと増大している (表 3).
| 媒体 - ESPN | 媒体 - Vouge | 広告主 - Nike | 広告主 - Gucci | 性別 - 男 | 性別 - 女 | |
|---|---|---|---|---|---|---|
| 媒体 - ESPN | - | $\left\langle \boldsymbol{v}_{e},\boldsymbol{v}_{v}\right\rangle$ | $\left\langle \boldsymbol{v}_{e},\boldsymbol{v}_{n}\right\rangle$ | $\left\langle \boldsymbol{v}_{e},\boldsymbol{v}_{g}\right\rangle$ | $\left\langle \boldsymbol{v}_{e},\boldsymbol{v}_{m}\right\rangle$ | $\left\langle \boldsymbol{v}_{e},\boldsymbol{v}_{f}\right\rangle$ |
| 媒体 - Vogue | - | - | $\left\langle \boldsymbol{v}_{v},\boldsymbol{v}_{n}\right\rangle$ | $\left\langle \boldsymbol{v}_{v},\boldsymbol{v}_{g}\right\rangle$ | $\left\langle \boldsymbol{v}_{v},\boldsymbol{v}_{m}\right\rangle$ | $\left\langle \boldsymbol{v}_{v},\boldsymbol{v}_{f}\right\rangle$ |
| 広告主 - Nike | - | - | - | $\left\langle \boldsymbol{v}_{n},\boldsymbol{v}_{g}\right\rangle$ | $\left\langle \boldsymbol{v}_{n},\boldsymbol{v}_{m}\right\rangle$ | $\left\langle \boldsymbol{v}_{n},\boldsymbol{v}_{f}\right\rangle$ |
| 広告主 - Gucci | - | - | - | - | $\left\langle \boldsymbol{v}_{g},\boldsymbol{v}_{m}\right\rangle$ | $\left\langle \boldsymbol{v}_{g},\boldsymbol{v}_{f}\right\rangle$ |
| 性別 - 男 | - | - | - | - | - | $\left\langle \boldsymbol{v}_{m},\boldsymbol{v}_{f}\right\rangle$ |
| 性別 - 女 | - | - | - | - | - | - |
| 媒体 - ESPN | 媒体 - Vouge | 広告主 - Nike | 広告主 - Gucci | 性別 - 男 | 性別 - 女 | |
|---|---|---|---|---|---|---|
| 媒体 - ESPN | - | $\left\langle \boldsymbol{v}_{e,P},\boldsymbol{v}_{v,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{e,A},\boldsymbol{v}_{n,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{e,A},\boldsymbol{v}_{g,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{e,G},\boldsymbol{v}_{m,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{e,G},\boldsymbol{v}_{f,P}\right\rangle$ |
| 媒体 - Vogue | - | - | $\left\langle \boldsymbol{v}_{v,A},\boldsymbol{v}_{n,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{v,A},\boldsymbol{v}_{g,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{v,G},\boldsymbol{v}_{m,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{v,G},\boldsymbol{v}_{f,P}\right\rangle$ |
| 広告主 - Nike | - | - | - | $\left\langle \boldsymbol{v}_{n,A},\boldsymbol{v}_{g,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{n,G},\boldsymbol{v}_{m,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{n,G},\boldsymbol{v}_{f,P}\right\rangle$ |
| 広告主 - Gucci | - | - | - | - | $\left\langle \boldsymbol{v}_{g,G},\boldsymbol{v}_{m,P}\right\rangle$ | $\left\langle \boldsymbol{v}_{g,G},\boldsymbol{v}_{f,P}\right\rangle$ |
| 性別 - 男 | - | - | - | - | - | $\left\langle \boldsymbol{v}_{m,G},\boldsymbol{v}_{f,P}\right\rangle$ |
| 性別 - 女 | - | - | - | - | - | - |
| モデル | パラメータ数 (次元) | 計算時間 |
|---|---|---|
| 線形 | $D$ | $O(\bar{D})$ |
| 2次交差項 | $D(D-1)/2$ | $O(\bar{D}^{2})$ |
| FM | $Dk$ | $O(\bar{D}k)$ |
| FFM | $DFk$ | $O(\bar{D}^{2}k)$ |
応用上のヒント
Juan, Lefortier, and Chapelle (2017) の応用例では, CTR 予測についてより具体的な応用例と, いくつかのテクニックを紹介している.
FFM は学習方法も, FM と同様にできる5. なお, Juan et al. (2016) は計算を効率化する工夫についても書いているが, 著者らがすでにプログラムを公開しているので, ここでは実装上の細かいテクニックの話は省略する.
ただし, 一方で空間計算量はロジスティック回帰より明らかに多い.
one-hot encoding ではなく ハッシュ変換 (Shi et al. 2009; Weinberger et al. 2009)) によって次元を線形モデルと同じになるように削減している.
$k$ はかなり小さくしてもうまくいったとしている. 特に FFM は計算量が多いのでこういう工夫は重要である.
正則化パラメータを調整するよりも, early stopping のほうが過学習 (過剰適合) の回避に効果的だったという.
Juan, Lefortier, and Chapelle (2017) の応用例では, 2次交差項を含むロジスティック回帰モデルに対して, 特に配信の少ない広告主の広告に対して CTR 予測の精度が向上していることを報告している. これは, 訓練データには現れない組み合わせの交差項が, FM ではうまく学習できるからだと著者らは考えている.
過去のモデルを更新する形で再学習する (warm-starting) のも有効
FFM (というかMF) は行列の非凸性を仮定している. よって非凸でないならば局所解に陥りうる. 最も簡単な解決方法は, 著者らがやっているように, 複数の初期値をランダムに決めて計算することである.
A/B テストでオンライン評価する際には, 計算時間の違いから更新頻度に差が出て不公平にならないよう, 更新タイミングを同期している. (計算の速さも重要な性能指標なので, 実用性で評価するならこの措置は不要な気がする.)
オリジナル
FM, FFM ともに考案者の実装が存在する. いずれもC++で書かれており, コマンドライン上で実行する使い方だが, 研究目的で作られたものなので民間企業でよくやるようなオンライン予測のような用途を想定しておらず, 使いづらい.
hivemall での利用
hivemall の場合は, FM, FFM はそれぞれtrain_fm() 関数でサポートされている.それぞれ, オリジナルのlibfm/libffmに沿ってJavaで実装している.
- Factorization Machine · Hivemall User Manual
- Field-Aware Factorization Machines · Hivemall User Manual
train_fm()は-f または –-factor オプションでベクトルの大きさ $k$ を調整できる. デフォルトは2-way FMのみで, 一般化された $M$-way FM は実装されていない(というかRendleらのlibfmも実装していない). train_ffm() 関数のオプションもtrain_fm()とほぼ同じである. FFMへの拡張にともなっていくつか増えたものとして, 例えば入力データのフィールド数を –-num-field で指定する必須の引数がある.
最近の研究動向
FM とニューラルネット
ここ数年はニューラルネット (NN) あるいはディープニューラルネット (DNN) に FM を取り入れようという研究も多く見られる. そのあたりに関して, 日本語で代表的な研究がリストアップされている.
https://data.gunosy.io/entry/deep-factorization-machines-2018#f-95055ec5ここによると, FMとDNNのあわせ技を提案した最初期の研究は Zhang, Du, and Wang (2016), Qu et al. (2016), Cheng et al. (2016), Guo et al. (2017) などがあるようだ6. そこで, ここで挙げられている研究を中心に調べてみる.
これらのうち, Zhang, Du, and Wang (2016) はFactorization-machine-supported Neuarl Network (FNN) と, FNN を少しアレンジした Sampling-based NN (SNN)を提案している. スケールの大きなカテゴリカル変数のデータを DNN でどう学習するかという観点で, FM を embedding 層の一種としてみなして書いている (これは他の研究でも同様) ため, FM の課題を発展解決させるという文脈とは目的意識が少し外れる研究だが, ZhangらがFNNを構想したきっかけが畳み込みニューラルネット (CNN) だという記述は興味深い. 彼らはCNNの最下層が局地的な隣接するニューロンのどうしの結合層であり, 一方でFMはフィールドごとの結合を見ているため, 両者は局所的な相関関係を学習しているという類似点があることに着目している. (こういうイメージは大雑把だが, 新しいアイディアに役に立つかもしれない.)
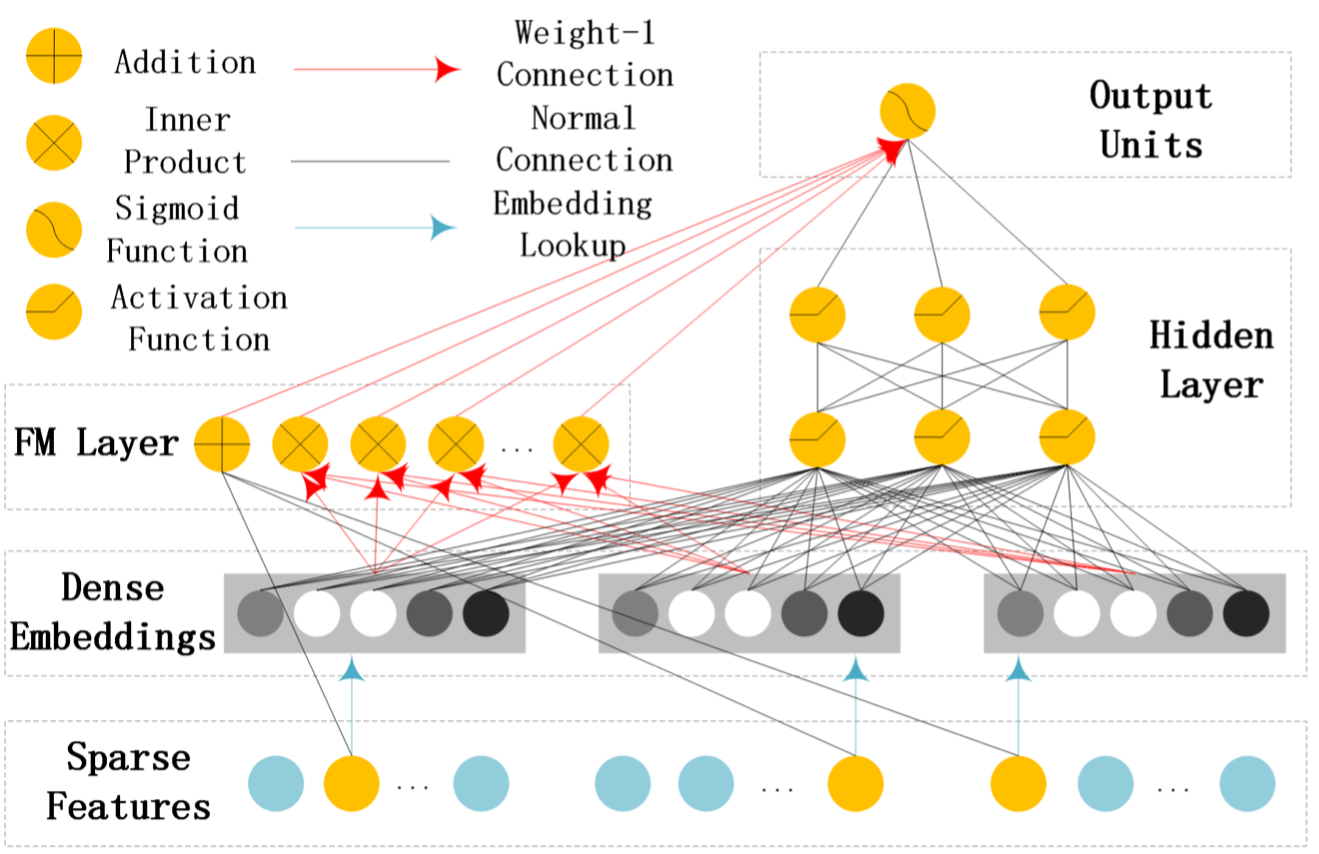
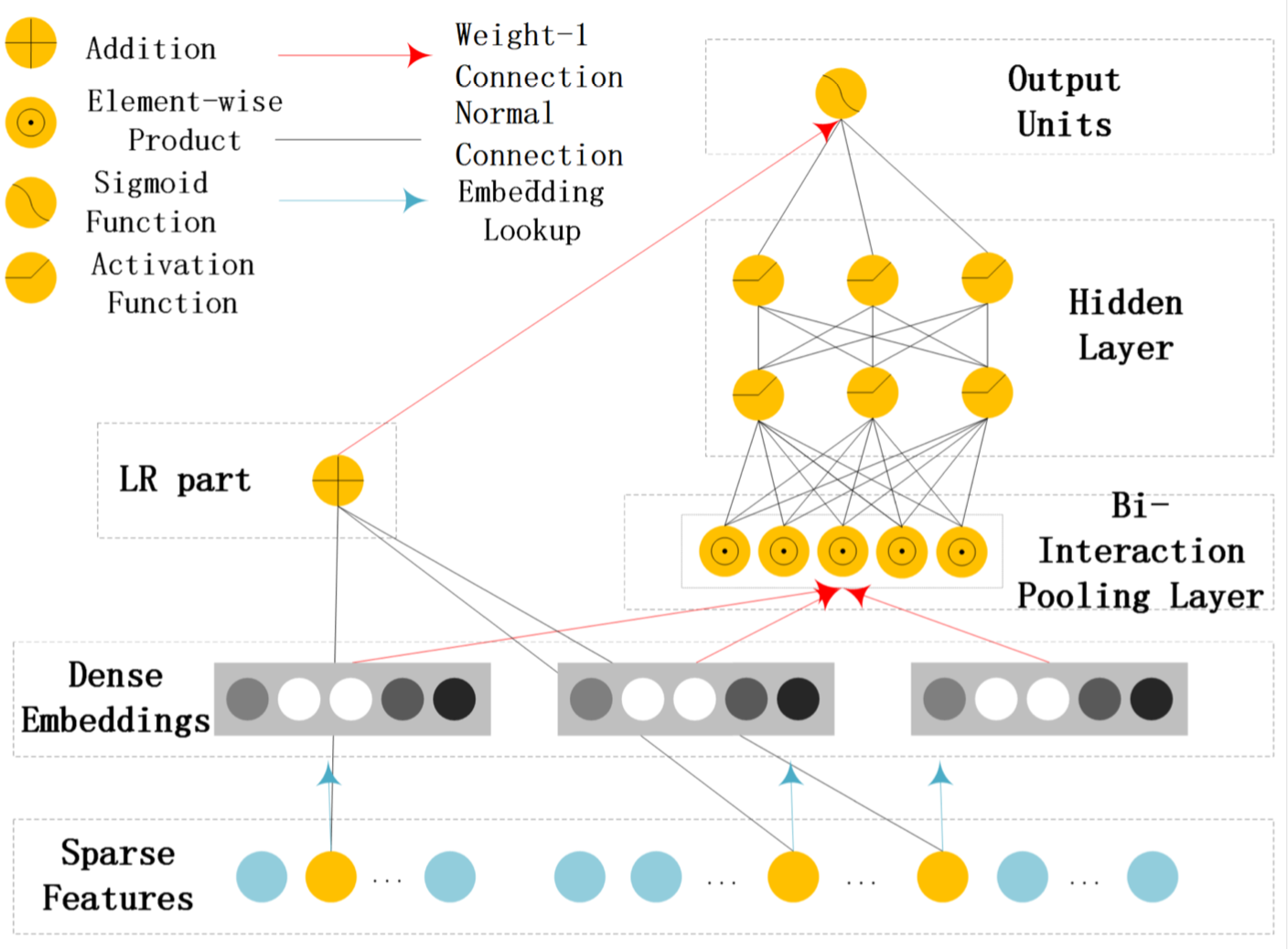
Guo et al. (2017) が提案したDeepFMは, 実質的にFMとDNNのコンポネントを並列した構造で, 最後の出力層でやっと両者を結合させることであえて低次元の組み合わせで表現できるようにしている (図 1). これに対し, He and Chua (2017) が提案した Neural FM (NFM) では, FM層 (bi-interaction polling 層と書いているが, 要するに 2-way FM) とDNNを直列にしている(図 2).
図 1: Guo et al. (2017) による DeepFM のネットワーク構造 (Zhang et al. 2019 より引用) 図 2: He and Chua (2017) による Neural FM のネットワーク構造 (Zhang et al. 2019 より引用)FFM の発展
さらにZhang et al. (2019) は, 既存のFMベースのネットワークの問題点を指摘し, FMではなくFFMを取り入れたField-aware Neural FM (FNFM) を提案している.
図 3: (Zhang et al. 2019) による Field-aware Neural FM (FNFM) のネットワーク構造 (Zhang et al. 2019 より引用)Zhang et al. (2019) の実験では, FM, DCN, DeepFM, NFM, など主要な競合モデルとも比較したが, いずれも少ないエポック数のうちに過学習が発生していることが示され, ごく小さな学習率 ( .0001 とか) を設定するのが望ましいとしている.
ここまで紹介した研究は, Criteo, Avazu, iPinYouなどのweb広告データによるクリック予測結果をベンチマークにしているが, 当てはまりの良さの向上の観点では, それぞれ顕著な進展があるとは言えない7ので, 自由度が大きすぎても学習が難しいのではないか?と思う.
ただし, 実験の課程でいくつか興味深い話はある.
Zhang, Du, and Wang (2016), He and Chua (2017) によれば, ドロップアウトが汎化に重要になる. 特に He and Chua (2017) は, L2 正則化よりもドロップアウトのほうがパフォーマンス向上に寄与したことを報告し, 著者らはその理由をドロップアウトは単に重みを抑制するのではなく部分モデルによるアンサンブル学習と同等のものとみなせるから, と推理している.
以下では, FM ではなく FFM とニューラルネットの研究に着目してサーベイをしている.
Field-awareなFactorization Machinesの最新動向(2019)
こちらで紹介されているものは, FFM で当初から問題とされていた過学習のしやすさをどう解決するかという研究が多く紹介されている.
参考文献
Cheng, Heng-Tze, Mustafa Ispir, Rohan Anil, Zakaria Haque, Lichan Hong, Vihan Jain, Xiaobing Liu, et al. 2016. “Wide & Deep Learning for Recommender Systems.” In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems - DLRS 2016, 7–10. Boston, MA, USA: ACM Press. DOI: 10.1145/2988450.2988454.
Duchi, John, Elad Hazan, and Yoram Singer. 2011. “Adaptive Subgradient Methods for Online Learning and Stochastic Optimization.” J. Mach. Learn. Res. 12 (July): 2121–59. http://jmlr.org/papers/v12/duchi11a.html.
Guo, Huifeng, Ruiming Tang, Yunming Ye, Zhenguo Li, and Xiuqiang He. 2017. “DeepFM: A Factorization-Machine Based Neural Network for CTR Prediction.” In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, 1725–31. Melbourne, Australia: International Joint Conferences on Artificial Intelligence Organization. DOI: 10.24963/ijcai.2017/239.
He, Xiangnan, and Tat-Seng Chua. 2017. “Neural Factorization Machines for Sparse Predictive Analytics.” In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval - SIGIR ’17, 355–64. Shinjuku, Tokyo, Japan: ACM Press. DOI: 10.1145/3077136.3080777.
Jahrer, Michael, Andreas Töscher, Jeong-Yoon Lee, J Deng, Jacob Spoelstra, and Hang Zhang. 2012. “Ensemble of Collaborative Filtering and Feature Engineered Models for Click Through Rate Prediction.” In KDDCup Workshop. https://www.semanticscholar.org/paper/KDD-Cup-2012-Track-2-\%3A-Ensemble-of-Collaborative-\%E2\%80\%94-Jahrer-T\%C3\%B6scher/05a8058916e7359e52eaee081e13194efdb21484.
Juan, Yuchin, Damien Lefortier, and Olivier Chapelle. 2017. “Field-Aware Factorization Machines in a Real-World Online Advertising System.” In Proceedings of the 26th International Conference on World Wide Web Companion - WWW ’17 Companion, 680–88. Perth, Australia: ACM Press. https://doi.org/10.1145/3041021.3054185.
Juan, Yuchin, Yong Zhuang, Wei-Sheng Chin, and Chih-Jen Lin. 2016. “Field-Aware Factorization Machines for CTR Prediction.” In Proceedings of the 10th ACM Conference on Recommender Systems - RecSys ’16, 43–50. Boston, Massachusetts, USA: ACM Press. DOI: 10.1145/2959100.2959134.
Juan, Yuchin, Yong Zhung, and Wei-sheng Chin. 2015. “Field-Aware Factorization Machines.” http://www.csie.ntu.edu.tw/~r01922136/slides/ffm.pdf.
Qu, Yanru, Han Cai, Kan Ren, Weinan Zhang, Yong Yu, Ying Wen, and Jun Wang. 2016. “Product-Based Neural Networks for User Response Prediction.” In 2016 IEEE 16th International Conference on Data Mining (ICDM), 1149–54. Barcelona, Spain: IEEE. DOI: 10.1109/ICDM.2016.0151.
Rendle, Steffen. 2010. “Factorization Machines.” In 2010 IEEE International Conference on Data Mining, 995–1000. Sydney, Australia: IEEE. DOI: 10.1109/ICDM.2010.127.
Rendle, Steffen, and Lars Schmidt-Thieme. 2010. “Pairwise Interaction Tensor Factorization for Personalized Tag Recommendation.” In Proceedings of the Third ACM International Conference on Web Search and Data Mining - WSDM ’10, 81. New York, New York, USA: ACM Press. DOI: 10.1145/1718487.1718498.
Shi, Qinfeng, James Petterson, Gideon Dror, John Langford, Alex Smola, and S.V.N. Vishwanathan. 2009. “Hash Kernels for Structured Data.” Jornal of Machine Learning Research 10 (December): 2615–37. http://www.jmlr.org/papers/v10/shi09a.html.
Wang, Ruoxi, Bin Fu, Gang Fu, and Mingliang Wang. 2017. “Deep & Cross Network for Ad Click Predictions.” In Proceedings of the ADKDD’17 on ZZZ - ADKDD’17, 1–7. Halifax, NS, Canada: ACM Press. https://doi.org/10.1145/3124749.3124754.
Weinberger, Kilian, Anirban Dasgupta, John Langford, Alex Smola, and Josh Attenberg. 2009. “Feature Hashing for Large Scale Multitask Learning.” In Proceedings of the 26th Annual International Conference on Machine Learning - ICML ’09, 1–8. Montreal, Quebec, Canada: ACM Press. DOI: 10.1145/1553374.1553516.
Zhang, Li, Weichen Shen, Jianhang Huang, Shijian Li, and Gang Pan. 2019. “Field-Aware Neural Factorization Machine for Click-Through Rate Prediction.” IEEE Access 7: 75032–40. DOI: 10.1109/ACCESS.2019.2921026.
Zhang, Weinan, Tianming Du, and Jun Wang. 2016. “Deep Learning over Multi-Field Categorical Data.” In Proceedings of 38th European Conference on IR Research, edited by Nicola Ferro, Fabio Crestani, Marie-Francine Moens, Josiane Mothe, Fabrizio Silvestri, Giorgio Maria Di Nunzio, Claudia Hauff, and Gianmaria Silvello, 9626:45–57. Paduva, Italy: Springer International Publishing. DOI: 10.1007/978-3-319-30671-1_4.
この話は, https://tech-blog.fancs.com/entry/factorization-machine の当該箇所が参考になる↩
より正確には, ゼロの要素は計算する必要がないため, $D$ を特徴量の非ゼロ成分の数の平均値 $m(\boldsymbol{x})$ に置き換えることができる.↩
実装は https://www.csie.ntu.edu.tw/~cjlin/libffm/ で公開されている.↩
ここではカテゴリカル変数のみの生データを one-hot encoding した例を挙げているが, 数値変数が含まれていても同様に扱える.↩
たとえば, Juan et al. (2016) では Duchi, Hazan, and Singer (2011) による AdaGrad を利用している.↩
その他, Wang et al. (2017) の Deep & Cross Network (DCN) は明示的に2次交差項をネットワーク構造に組み込んでいるので, [eq:polynomial2] のニューラルネット版と言えるかもしれない.↩
例えば, ここまでで紹介した研究では, Wang et al. (2017) によって提案された, FM ではなく2次交差項モデルと同様な構造に制約した Deep & Cross NN (DCN) もよく比較対象に挙げられており, それとも大きな違いが出ていない↩