はじめに
こんにちは。ぐぐりら(guglilac)です。
今回は最近興味を持って調べているField-awareなFactorization Machinesの近年の動向をまとめてみようと思います。
Factorization Machinesが提案された2010年から、Factorization Machines関連の研究はいくつかの方向に進んできました。
例えば、Factorization MachinesをDeep Learningと組み合わせた研究はその主流の一つで、xDeepFM [Lian+, KDD2018]までの流れが以下の記事でまとめられています。
DeepなFactorization Machinesの最新動向 (2018)
今回紹介するFieldという概念に関わるFactorization Machinesは、Deep + Factorization Machinesとは別に発展してきた研究の方向の一つです。
2016年に発表されたField-aware Factorization Machines (FFM) [Juan+, RecSys2016]から派生した研究はいくつか存在し、2019年現在もいわゆるTop Conferenceに採択される論文にはField関連のFactorization Machinesの名前が含まれているものが複数あります。
今回の記事は2016年~2019年の間に発表されたField-aware Factorization Machinesから派生した研究をいくつかまとめていきたいと思います。
何かしらおかしなところ、疑問、コメント等あればご指摘よろしくお願いいたします!
Factorization Machines[Rendle, ICDM2010]とは
まず、Field-aware FMの説明に入る前に簡単にFactorization Machines(FM)自体の紹介をしたいと思います。
FMは特徴量どうしの交互作用を考慮するためのモデルであり、予測モデルとしてはとてもpopularなモデルで、XGBoostなどと並びとりあえず試してみるべき手法として知られています。
ここでいう交互作用とは、例えば年齢という特徴と性別という特徴の組み合わせのことで、これらの組み合わせが予測へ効いてくることは十分あり得ます。
単純な線形回帰では特徴量の交互作用を学習できません。この交互作用をうまくモデリングしようという思想から、FMが研究されています。
さて、単純に交互作用を考慮したモデルを作ろう、と思った時に
f(x)=w_0 + \sum_{i=1}^d w_ix_i + \sum_{i,j}w_{i,j}x_ix_j
のように線形項に加えて特徴量$x_i,x_j$の交互作用を$w_{i,j}x_ix_j$として扱うモデルが一番最初に思い浮かぶと思います。
ですが、これだと特徴量の個数が$d$個あると項の個数は$O(d^2)$で増えていきます。その分重み$w_{i,j}$も増えていきます。
また、ナイーブに交互作用をモデリングすることのデメリットには、学習すべき重みの個数が増えることの他に、学習時に現れなかった特徴量の組み合わせの重みが学習できないということが挙げられます。
このように、ナイーブに交互作用をモデリングすると、
- 学習すべきパラメータが多い
- 汎化性能が低い
といったデメリットがあります。
一方、FMでは特徴量$x_i,x_j$の交互作用に対応する重み$w_{i,j}$をベクトル$v_i,v_j$の内積で置き換えます。
f(x)=w_0 + \sum_{i=1}^d w_ix_i + \sum_{i,j}\langle v_i,v_j \rangle x_ix_j
$v_i$は特徴量$x_i$に対応する低次元のベクトルで、embeddingとかlatent vectorなどと呼ばれます。
このように単一の重み$w_{i,j}$をそれぞれの特徴量のembeddingの内積に分解すること(factorizeする)ことで、embeddingの次元を$K$とすればパラメータの個数は$O(d^2)$から$O(dK)$となります。
一般に高次元の特徴量を用いることが多いため$d$は大きく、embeddingの次元$K$は低次元にするので、大きく学習すべきパラメータの個数を削減できます。
また、ナイーブなモデルの二つ目のデメリットである汎化性能の低さも改善することができています。
なぜなら、ある特徴量の組$x_i,x_k$が学習データに含まれていなかったとしても、$x_i,x_j$の組と$x_j,x_k$の組が含まれていれば、それぞれのembeddingである$v_i,v_j,v_k$を学習することができ、得られた$v_i,v_k$の内積で(ある程度)特徴量の組$x_i,x_k$の交互作用を捉えることができると考えられるからです。
Field-aware Factorization Machines (FFM) [Juan+, RecSys2016]
次に、今回のテーマであるField-aware FM (FFM)について紹介します。
FFMの説明をする前に、Fieldとは何かを説明します。
入力がカテゴリカルな特徴量の場合、それぞれの特徴量をone hot化してconcatしたものをモデルに入力することが多いです。
例えば、特徴量が(性別、国籍、職業)のようなカラムを持っていたとして、
男性 -> [0,1]
女性 -> [1,0]
日本 -> [0,0,...,1,0,...,0]
アメリカ -> [1,0,...,0]
エンジニア -> ...
医者 -> ...
のようにone hotになったとき、男性かつ日本国籍かつエンジニアの人は入力がそれぞれone hot化したベクトルをconcatしたものになる、といった感じです。
Fieldとはこの性別や国籍、職業などのone hotされた時のかたまりの単位です。one hotされたベクトルはどのField由来なのかという単位で分割できるというわけです。
Fieldの紹介が終わったので、Field-aware FMの話に入ります。
FMでは、各特徴量のembeddingは一本のベクトルで、他のどの特徴量との交互作用を考える時も特徴量$x_i$のembeddingはいつも$v_i$でした。
しかし、よく考えてみると、特徴量$x_i$の交互作用の仕方は交互作用する相手のFieldによって変わりそうです。
男性という特徴は職業と国籍で違った交互作用をしそうだよね、ということです。
それを一本のembeddingで扱うのは難しい、ということでFFMでは交互作用する相手のFieldの個数分embeddingを用意するという方法を提案しています。
男性という特徴に対応するembeddingがFMでは一本でしたが、対国籍Field用と職業Field用の二つのembeddingを学習する、という手法になります。
定式化すると、このようになります。
f(x)=w_0 + \sum_{i=1}^d w_ix_i + \sum_{i,j} \langle v_{i,F(j)},v_{j,F(i)} \rangle x_ix_j
$F(i)$は$x_i$が属するFieldとし、$v_{i,F(j)}$は特徴量$x_i$の、Field $F(j)$用のembeddingを表します。
論文の詳しい内容が知りたい方はこちらを参考にしていただければと思います。
【論文紹介】Field-aware Factorization Machines for CTR Prediction (RecSys2016)
FFMの弱点
先述したように、FFMはFieldの情報を入れてFMを改善しました。
しかし、
Fieldの個数はfeatureの個数よりずっと少ないのですが、それでもパラメータの増加は大きな問題です。
実際、FFMはそのモデルの構成からわかる通りとても表現力があり、過学習しやすいという弱点があることが指摘されています。
今回以下で紹介する論文として、主に二つの観点でFieldと関連したものを持ってきました。
- Field-aware Probabilistic Embedding Neural Network (FPENN)[Liu+, RecSys2018]
- Field-weighted Factorization Machines (FwFM) [Pan+, WWW2018]
- Interaction-aware Factorization Machines (IFM) [Hong+, AAAI2019]
- Field Attentive Deep Field-aware Factorization Machine (FAT-DeepFFM) [Zhang+, ICDM2019]
一つ目は、FFMの弱点であるパラメータ数が多く過学習しやすい点を改善するもので、前半の二つが
該当します。
もう一つはAttention + FMにFieldの概念を取り入れるもので、後半の二つです。
Field-aware Probabilistic Embedding Neural Network (FPENN) [Liu+, RecSys2018]
Field-aware Probabilistic Embedding Neural Network (FPENN)は、FFMの過学習を防ぐモデルへの改善を目的として考案されたモデルです。
FPENNでは、FFMのように特徴量につきField分のembeddingを学習するという点では一緒ですが、そのembeddingを直に学習するのではなく、そのembeddingが従う確率密度分布のパラメータを推定する、という方法で学習します。
このようにembeddingに確率的なゆらぎをもたせることで、学習時に含まれるノイズに過度にfitせずに汎化性能を高めることができる、という寸法です。
embeddingはFFMの様に線形項と交互作用項に使われる他に、deepなcomponentにも入力され、それぞれの出力をまとめて最終的な出力としています。Deepとの組み合わせ方は、DeepFM [Guo+, IJCAI2017]を参考にしているようです。
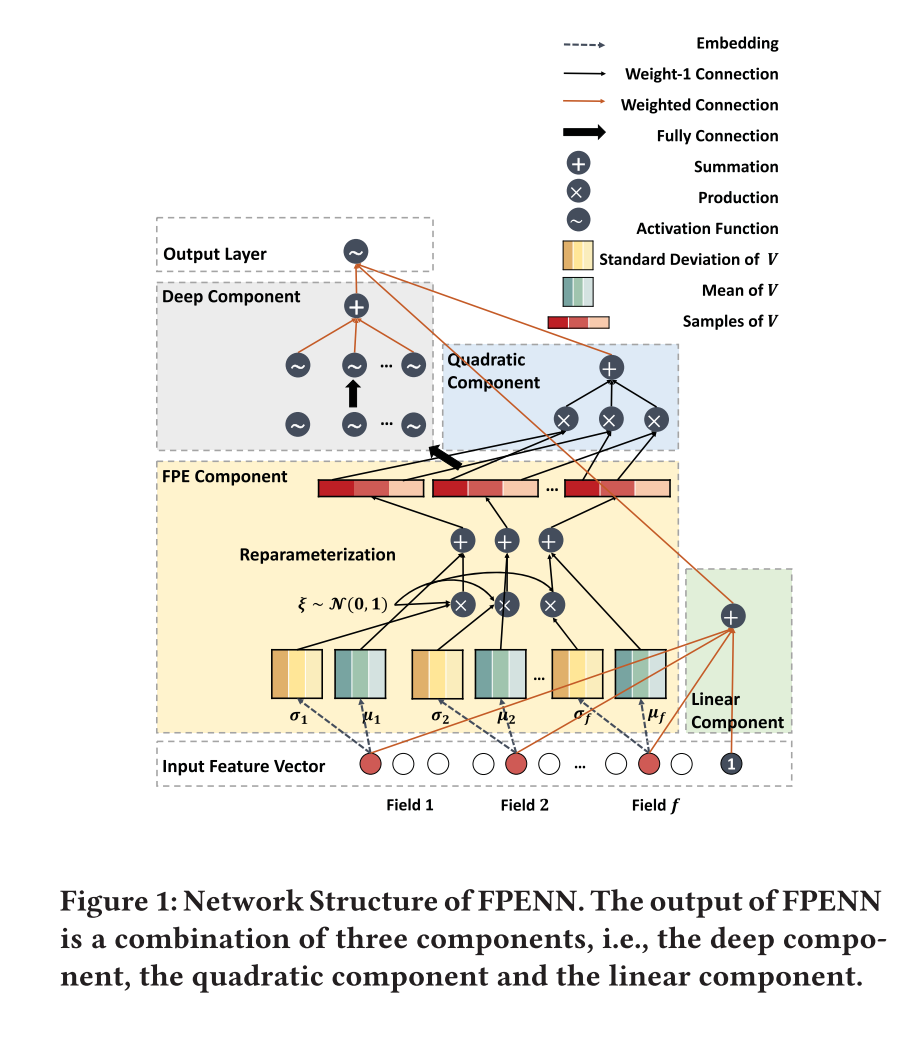
学習した確率密度分布(論文中では共分散行列が対角行列の多次元ガウス分布)のパラメータに従うembeddingをサンプルする部分をナイーブに実行するとback propagationできなくなってしまうのですが、
embeddingの従う確率密度分布のパラメータの学習にはReparameterization trickを用いています。
Reparameterization trickはVariational Auto Encoder (VAE)の学習で使われています。
この辺りの記事がわかりやすいと思います。
実験では、FFMは学習を進めるとすぐ過学習するのに対し、FPENNは学習を続けてもvalidation lossがあまり上がらない、という結果が出ています。
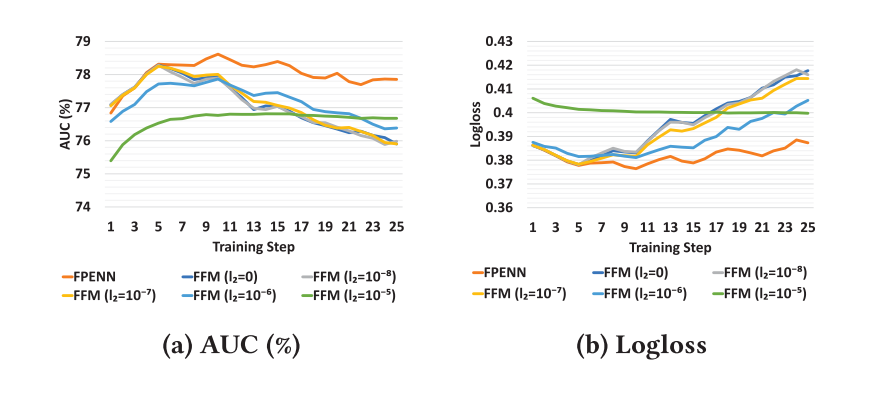
Field-weighted Factorization Machines (FwFM) [Pan+, WWW2018]
FPENNとは別の方法で、 FFMの過学習問題を改善した研究にField-weighted Factorization Machines (FwFM)があります。
FwFMでは、FFMのパラメータ数をいかにして減らすか、という部分で改善を施しています。
振り返りになりますが、FFMでは各特徴量に対して相手のFieldごとに異なるembeddingを学習していました。
これは、相互作用する相手のFieldごとに交互作用の仕方が違う、という点を考慮するために考えられたモデルですが、この交互作用の仕方が違う、という部分をFieldのpairごとに予測への寄与が異なると考え直したのがFwFMです。
FFMはFieldごとに異なるembeddingを用意するから内積でよしなに学習してね、というモデルで、この「内積でよしなに学習する」べき部分って大部分が「Fieldのpairごとに異なる予測への重要度」だよね、じゃあこれをexplicitに重みにしてmodelを作ればいいよね、という気持ちです。
実際、Fieldのpairごとに異なる予測への重要度がどれくらいFieldの組ごとに異なるのかをヒートマップにしたものをみると、大きく異なっていることがわかります。
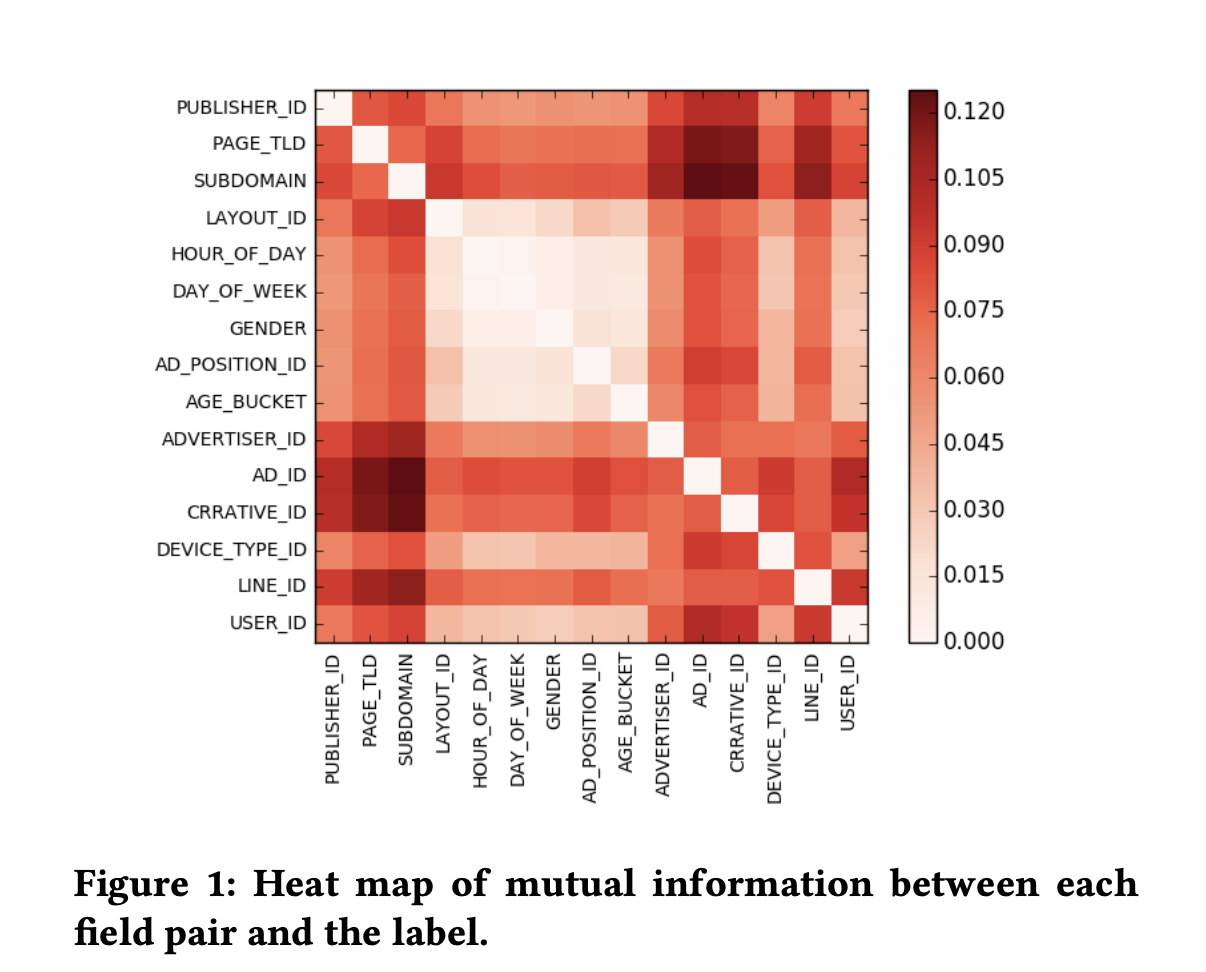
これを定式化するとこの様になります。
f(x)=w_0 + \sum_{i=1}^d w_ix_i + \sum_{i,j} \langle v_i,v_j \rangle x_ix_jr_{F(i),F(j)}
FFMとは異なり、embeddingは特徴量につき一つです。
FMと比較して、$r_{F(i),F(j)}$が新しく追加されています。これがField $F(i)$と$F(j)$の交互作用の重要度を表す重みです。
FFMと比較すると、FwFMはFFMのField分のembeddingが全て互いに定数倍の関係にあるようなembeddingに制限しているモデルと解釈できます。
FFMのうち重要そうな部分だけに制限をかけたモデル、と捉えると面白いですね。
この他にも、通常のFMでは線形項ではembeddingではなく元の特徴量を入力にしていますが、今回の研究では線形項の部分もembeddingを使ってモデリングするという手法も提案しています。
詳しくは自分のブログの記事を参考にしていただければと思います。
ところで、この「Field pairごとに重要度を表す重みを導入する」という部分、自分は読んでいて引っかかりました。
「ん?これってFMがナイーブに交互作用を考えていたときに直接重みを考えていたのと似てる?じゃあこれFieldごとのembeddingにfactorizeするっていうアイデアもありでは??」
と考えました。Fieldの個数が多かったり、学習時に現れないFieldのpairがあるわけではないので改善する理由は特に見当たりませんが、Fieldの個数が多い場合にはfactorizeするとパラメータ数が削減できそうです。
と考えていたらやはりFieldへのembeddingを考える研究がありました。それが次の研究です。
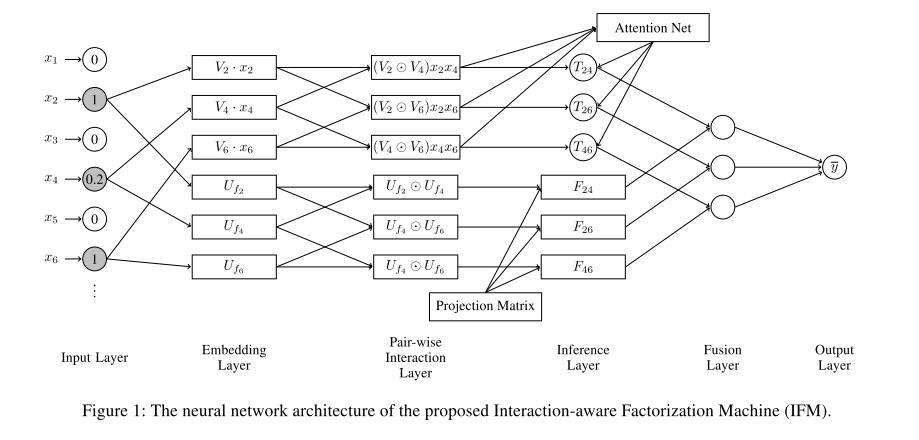
Interaction-aware Factorization Machines (IFM) [Hong+, AAAI2019]
こちらの研究は、FFMの過学習問題を防ぐというよりは、よりよくAttention + FMを組み合わせる方法を調べる、という研究になっています。
Attention + FMの手法の研究はAttentional FM (AFM)[Xiao, IJCAI2017]がありますが、AFMとは異なり今回の研究はFieldの情報を組み合わせたものを提案しています。
IFMでは、feature levelとfield levelのattentionを考慮するモデルを考えています。
まず、featureとfieldのembeddingをそれぞれ得ます。featureのembeddingはFMと同じく特徴量につき一本です。
この「Fieldのembeddingを考えること」が先ほどFwFMで述べたField pairのFactorizeに対応します。
feature levelとfield levelのembeddingを得たら、交互作用を考えたいので内積をとります。
モデルのアーキテクチャ上、交互作用をスカラーではなくベクトルで欲しい!みたいなときは要素積をとります。
この辺りは些細なので詳しくは別の記事に譲るとして、ポイントは
- featureもfieldもembeddingする
- それらの交互作用からそれぞれのlevelのattentionを計算する
- それぞれのattentionで特徴量のペアを重み付けて予測に使う
という構成になっている部分です。
得られたembeddingや交互作用はここでもDeepFM [Guo+, IJCAI2017]を参考にしたモデルに使われます。
先ほど述べた、「fieldのembeddingを考えて、pairの交互作用は内積や要素積で表現する」というFieldに関してのFactorizationのメリットはFieldが多いときにパラメータ数が削減できるってことが挙げられます。
この論文では特にそれについての言及はありませんでした。(し、FwFMがそもそも引かれていない)
Field Attentive Deep Field-aware Factorization Machine (FAT-DeepFFM) [Zhang+, ICDM2019]
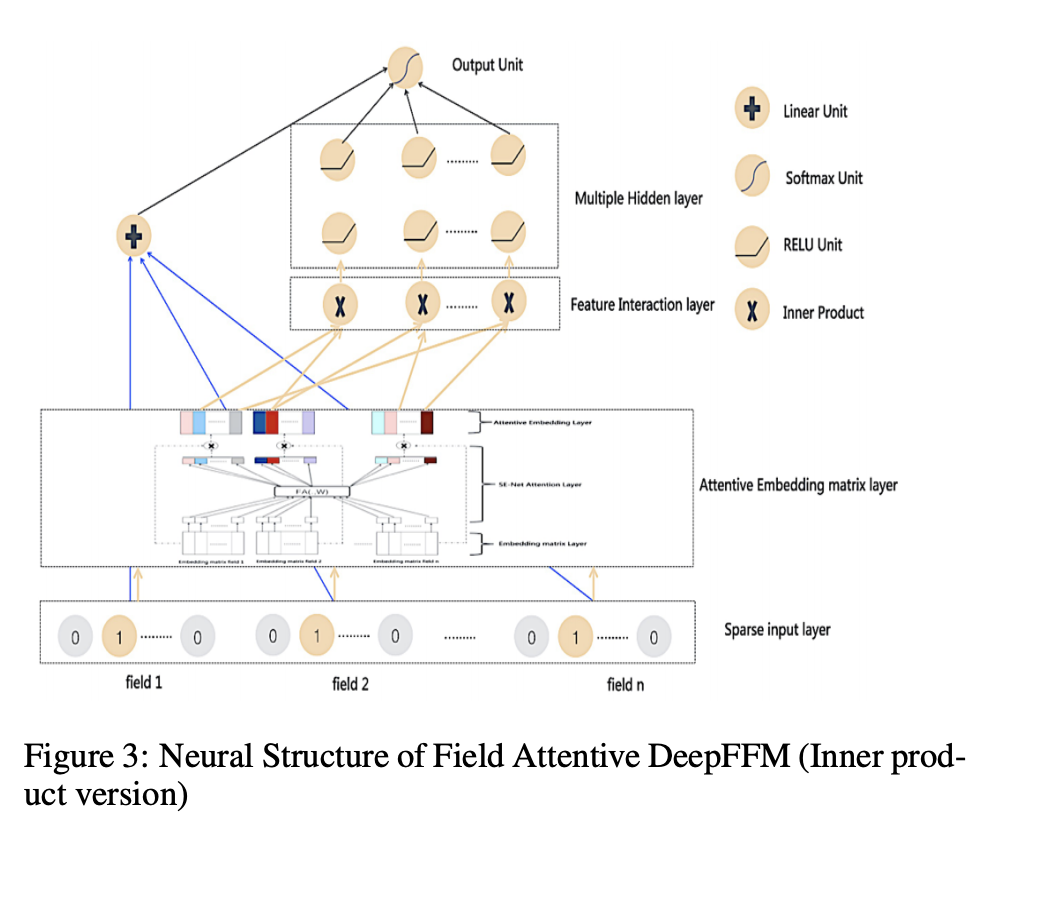
最後は、Field Attentive Deep Field-aware Factorization Machine (FAT-DeepFFM)です。これもFMMにAttentionをつけてみよう、という研究です。
先ほど少し述べたAttentional FM(AFM)[Xiao, IJCAI2017]では、featureの交互作用項たちを入力としてAttentionを計算し、重要なfeatureのinteractionにhighlightするように学習する、というモデルでした。
AFMからのFAT-DeepFFMの差分は
- FFMのように交互作用する相手のFieldの個数分embeddingを用意する(FFMなので当たり前)
- Fieldの情報をAttentionに入れるという部分
- 交互作用後ではなくembeddingの時点でattentionする
です。
Attentionの計算には、ILSVRC 2017 画像分類 Top の手法であるSqueeze-and-Excitation Networks[Hu+, CVPR2018]を参考に作ったCE-netというものを使います。(詳しい説明は他の記事でお願いします。)
Attentionを交互作用の前にいれる(embeddingの時点で入れる)か後に入れるかの比較が実験でなされていて、CE-netをAFMの様に交互作用のあとにいれるものも試していますが、実験ではembedding時点でattentionをかけた方がいい結果が出たそうです。Deep learningむずかしい。。。

MLP-やCE-が交互作用の後にAttentionを入れているもので、どちらもembedding時点でAttentionを入れている提案手法に劣っています。
まとめ
今回はFactorization Machinesから始まり、Fieldの情報を用いた改善を行ったField-aware FMを紹介し、FFMから派生した研究として四つの論文を紹介しました。
冒頭で述べた通り、 Deep + FMの発展もこれとは別に行われており、記事中でもちらほらDeepFMなどのDeepモデルと組み合わせた手法が提案されていました。
これまでのField awareなFMの発展はDeep + FMの発展とは基本的に直交するため、今後両方の観点から工夫されたモデルが出てくることを考えるとだいぶカオスになってきそうですね。
紹介した順番でも前に持ってきた二つの研究のような、改善が明確でモデルがあまり複雑ではないものを読むと面白いなあと感じます。
今後もFM関連の研究はチェックしていきたいと思います。
長くなりましたが、最後までお読みいただきありがとうございました。
(宣伝)
普段は機械学習やプログラミングに関する技術ブログを書いています。
よろしければどうぞ!
参考文献
- [Lian+, KDD2018] Jianxun Lian, et al. "xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems" KDD, 2018.
- [Rendle, ICDM2010] Steffen Rendle. "Factorization Machines" ICDM, 2010.
- [Juan+, RecSys2016] Yuchin Juan, et al. "Field-aware Factorization Machines for CTR Prediction" RecSys, 2016.
- [Liu+, RecSys2018] Weiwen Liu, et al. "Field-aware Probabilistic Embedding Neural Network for CTR Prediction" RecSys, 2018.
- [Guo+, IJCAI2017] Huifeng Guo, et al. "DeepFM: A Factorization-Machine based Neural Network for CTR Prediction" IJICAI, 2017.
- [Pan+, WWW2018] Junwei Pan, et al. "Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising" WWW, 2018.
- [Xiao+, IJCAI2017] Jun Xiao, et al. "Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks" IJCAI, 2017.
- [Hong+, AAAI2019] Fuxing Hong, et al. "Interaction-aware Factorization Machines for Recommender Systems" AAAI, 2019.
- [Hu+, CVPR2018] Jie Hu, et al. "Squeeze-and-Excitation Networks" CVPR, 2018.
- [Zhang+, ICDM2019] Junlin Zhang, et al. "FAT-DeepFFM: Field Attentive Deep Field-aware Factorization Machine" ICDM, 2019.