はじめに
以下の記事によると、ニューラルネットワークは任意の関数を表現できるということである。
http://nnadl-ja.github.io/nnadl_site_ja/chap4.html
ずいぶんと昔に数学の先生に任意の関数は高次の関数(例:a0+a1×X^1+a2×X^2)で表現できると聞いたことがあった。しかしながら、ニューラルネットワークの基本形である線形関数と(Y=wX+b)と活性化関数(シグモイド関数)を複数重ねただけで任意の関数が表現できるとこの記事はいう。説明そのものは理解できないものではないのだが、線形関数が曲がるわけがないと思っているのでどうしても信じがたい。そこで、tensorflowを使って実験をすることにした。
実験の前提条件
OS:Win10(64bit)
開発環境 : python3.6 + tensorflow1.2
実験用データは、Sin関数を使って生成したデータにノイズを混ぜたものにした。これによって学習後のモデルが過学習の傾向を示すかどうかを視覚的にわかるようにした。つまり、正解であるSin関数の波形が表現できていればOkだが、ノイズを拾って学習すると見た目がSin関数から外れていくことになる。
データはXについては0~6を0.02刻みとし、yは先に示した通り、Sin関数のアウトプットにノイズを加えた。念のため、切片も加えてみた。
こうして生成した300件のデータからランダムに120件を抽出し学習データとする。
以上をコードにしたものを次に示す。
input_data = np.arange(0,6,0.02) # Xの生成
output_data = np.sin(input_data) + 1 + np.random.randn(input_data.size)/3 # Y生成
dataset = np.vstack((input_data , output_data))
idx = np.random.choice(300,120) # ランダムに作成したデータから一部を選択
idx.sort()
dataset_mini = dataset[0: , idx]
train_x = dataset_mini[0].reshape(120,1)
train_y = dataset_mini[1].reshape(120,1)
参考として生成したデータの分布を示す。

見ようによっては、3次曲線と思える分布が取得できた。ニューラルネットが3次曲線に近似したものになれば、学習は成功である。しかしながら、ほぼ直線に近いものになっていたり、分布に合わせてジグザグなものになるようであれば、成功とはいえない。
モデルの構築
ニューラルネットワークのモデルであるが、隠れ層は先の記事にあるように1層とする。この隠れ層のノードであるが、データの分布が0からスタートして右上がり、右下がり、右上がりという傾向を示していることから最低でも3つの線形関数が必要と予測されることからノード数のベースを3とする。とりあえず、試行の1回目ということもあり、この3に予備的に2を加えたノード数から初めて、学習程度から増減させるという方法で進めることにする。
隠れ層の活性化関数はsigmoid関数を使用する。他の活性化関数を使用した場合については、実験結果を踏まえて実施要否を判断する。
損失関数は最小二乗誤差を用い、最適化関数は学習率を気にする必要のないAdamを用いる。
以上をコードにしたものを次に示す。
# inputの格納領域を定義
x = tf.placeholder(tf.float32,[None,1])
# ウェイトの初期値をゼロとして定義
w1 = tf.Variable(tf.truncated_normal([1,5]))
b1 = tf.Variable(tf.zeros([5]))
w2 = tf.Variable(tf.truncated_normal([5,1]))
b2 = tf.Variable(tf.zeros([1]))
# モデルの定義
y0 = tf.nn.sigmoid(tf.matmul(x ,w1) + b1)
y1 = tf.matmul(y0,w2) + b2
# 観測値の格納領域を定義
y = tf.placeholder(tf.float32,[None,1])
# 損失関数を二乗誤差和として定義
loss = tf.reduce_sum(tf.square(y1-y))
# トレーニングアルゴリズムを定義
train_step = tf.train.AdamOptimizer().minimize(loss) # Adamを使って損失関数の値を最小化するように最適化する
学習プロセスであるが、データ件数が120件と少数なのでミニバッチを使用しないことにする。学習回数は10,000回をベースにして、収束状況を見ながら調整する。
# トレーニング環境の定義
sess = tf.Session()
# 変数の初期化
sess.run(tf.global_variables_initializer())
# 学習の実施
i=0
for _ in range(10000):
i=i+1
sess.run(train_step , feed_dict={x:train_x , y:train_y}) # 所定のアルゴリズムにて学習実行
if i % 500 == 0 :
loss_val = sess.run(loss,feed_dict={x:train_x,y:train_y}) # 損失関数を計算
print('Step : %d, loss : %f' % (i,loss_val))
実験結果
まず、損失関数の収束状況であるが、次のように収束しているといってよいであろう。8,000回から10,000回の収束状況を見ると、さらに学習回数を増やせばより小さい値に近づくことがうかがえる。
Step : 500, loss : 55.952148
Step : 1000, loss : 37.403114
Step : 1500, loss : 29.274075
Step : 2000, loss : 25.615166
Step : 2500, loss : 23.357674
Step : 3000, loss : 21.246296
Step : 3500, loss : 19.382114
Step : 4000, loss : 17.950485
Step : 4500, loss : 16.868690
Step : 5000, loss : 16.006006
Step : 5500, loss : 15.290855
Step : 6000, loss : 14.695663
Step : 6500, loss : 14.208690
Step : 7000, loss : 13.818590
Step : 7500, loss : 13.477202
Step : 8000, loss : 12.306458
Step : 8500, loss : 11.863388
Step : 9000, loss : 11.507794
Step : 9500, loss : 11.225819
Step : 10000, loss : 10.998775
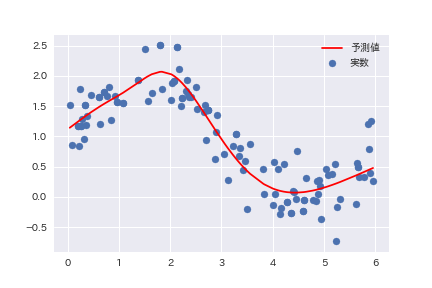
学習結果として得られた曲線は以下のようになった。
まず、それなりに高い説明力のある曲線が生成されていることが読み取ることができる。曲線そのものは、Sin関数というよりも3次曲線に近いように見える。X=0からX=2あたりが若干直線的となっていることが気になる程度である。
学習回数を減少させると未学習の傾向を示す。5,000回にしたところ、次のような結果となった。
本実験の場合、正解がわかっているため、未学習であると判断できるが、グラフだけで判断する限り、それほど誤ったものとは言えない程度の未学習状況である。
反対に学習回数を増やすとどのようになるのかを確認するため、100,000回にしたところ、次のような過学習の傾向となることがわかる。
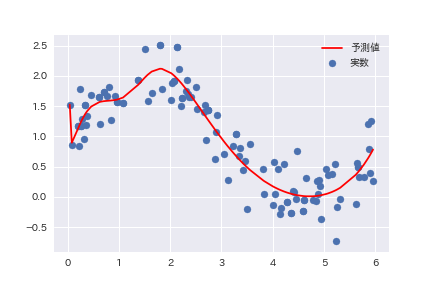
以上より、今回のようなデータの場合、10,000回程度で十分な学習結果を得ることができるということができる。この10,000回という回数は、データ件数120件からすると、かなり大きい印象を持つ。言い換えると、ニューラルネットワークで回帰を行うと、それだけの計算量が必要とされることになる。学習データが数万件単位となった場合のことを考えると、あまり実務的とは言えないように思われる。
次に隠れ層のノードを調整する。まず、最低限数にあたるノード数=2として学習回数=20,000とした結果、以下の結果が得られた。
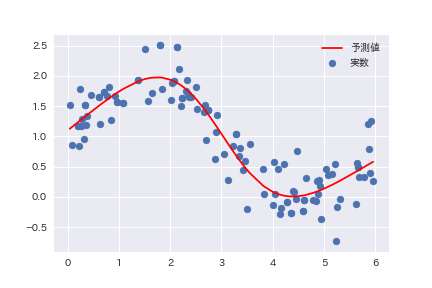
これより、ノード数は必要最低限の2であっても十分な説明力を持つことがわかる。
最後に学習済みのモデルに対して実験用データ全件(300件)を入力データとして用いた結果を示す。

過学習とはいえない程度の適合であり、完成したモデルは十分に実用に耐えるように思われる。
まとめ
まず、当初の実験目的である任意の関数をニューラルネットワークが表現することができるかどうかについては、可能であることが実証できた。また、その結果であるが、polynominal-Regressionの場合と比較してほど同等のものである。(下図参照)
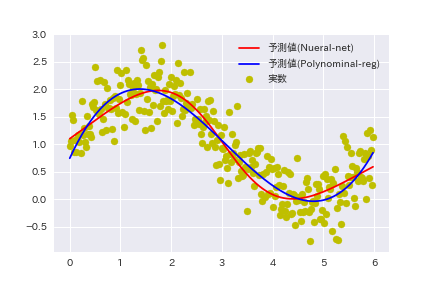
ただし、ニューラルネットワークは学習にある程度の時間(あるいはコンピュータリソース)を必要とする。したがって、比較的簡易なものの場合は従来の機械学習技術を用いたほうが簡単に結果が得られると思われる。