因子分析を概説しつつ、Pythonで動かしてみよう記事です。
因子分析の概要
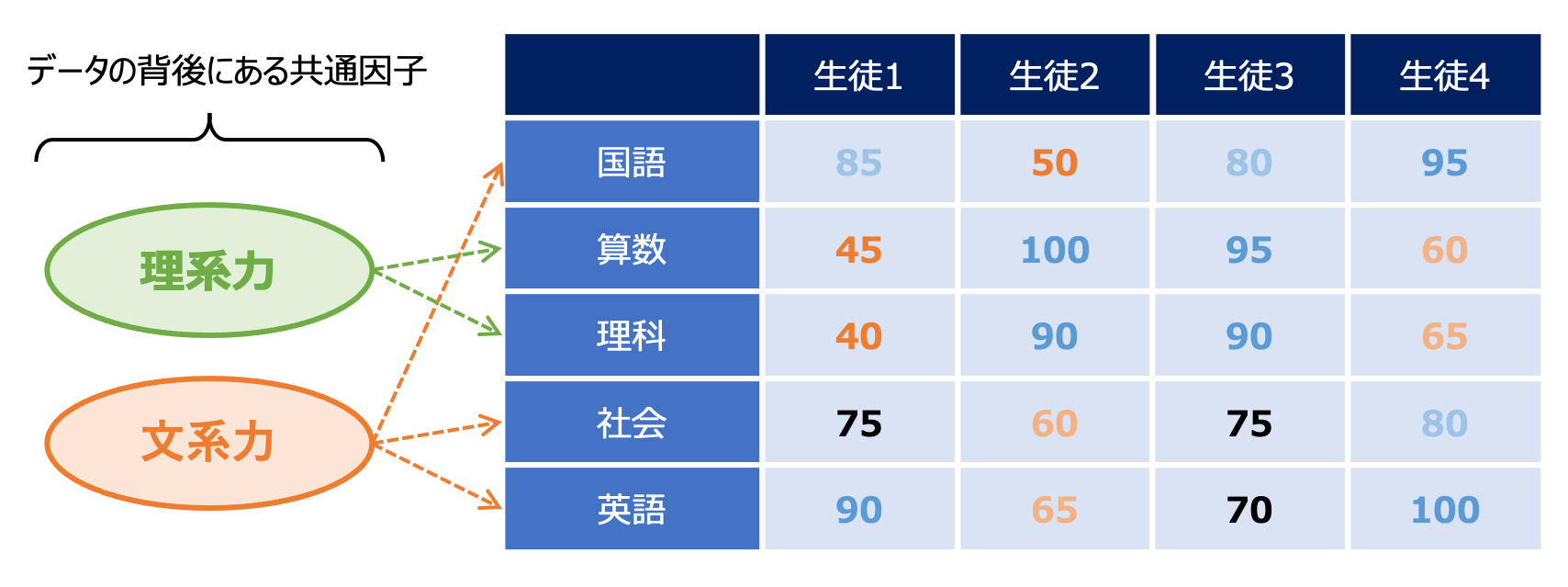
多数の特徴量からなるデータから、特徴量間の共通の因子を探り出し、少数の共通因子によってデータを単純化する手法を因子分析 (factor analysis) といいます。
5教科のテストをn人の生徒が受験した時、各科目の点数はそれぞれ独立に決定されるわけではなく、例えば「理系の能力」が高い人は「数学」と「理科」の点数がともに高い傾向にあり、「文系の能力」が高い人は「国語」「英語」「社会」が高くなる傾向にあると考えられます。このように「理系の能力」「文系の能力」といった共通の要因を共通因子 (common factor) といいます。
「理系の能力」「文系の能力」といった因子の各生徒が持つ値を因子スコア (factor score) といい、今、生徒iのk番目の因子スコアを$f_{ik}$と表すことにします。このとき、K個の因子の存在を仮定するモデル (K因子モデル) において、(生徒i, 科目j) の点数$x_{ij}$は以下のように表されます。
$$x_{ij}=a_{j1}f_{i1}+...+a_{jK}f_{iK}+d_{j}u{ij}$$
ここで$a_{jk}$は因子負荷量と呼ばれ、因子分析で推定される対象になります。また$d_{j}u{ij}$の項は共通因子では説明できなかった部分を表しており、$u{ij}$は独自性因子、$d_{j}$は独自係数などと呼ばれます。
上の式を行列で表現すると以下のようになります。
$$X=FA^{\mathrm{T}}+UD$$
因子負荷量を要素に持つ$A$を因子負荷行列といいます。
なお、因子の解釈が分かりやすくなるような座標軸を探索する回転 (rotation) という操作がありますが、本記事では触れません。有名なものとしてはバリマックス回転 (varimax rotation) などがあります。
それでは実際にデータを使って因子分析を試してみましょう!
使用するデータセットについて
イタリアの同じ地区で生産された3つの異なる品種のワインの化学分析結果に関するデータです。説明変数として以下の13個の特徴量があり、目的変数としてワインの品種 (class_0, class_1, class_2) が用意されています。データサイズは178です。
| 変数名 | 意味 |
|---|---|
| alcohol | アルコール度数 |
| malic_acid | リンゴ酸 |
| ash | 灰 (?) |
| alcalinity_of_ash | 灰 (?) のアルカリ度 |
| magnesium | マグネシウム |
| total_phenols | 総フェノール類量 |
| flavanoids | フラボノイド (ポリフェノールの一種) |
| nonflavanoid_phenols | 非フラボノイドフェノール類 |
| proanthocyanins | プロアントシアニジン (ポリフェノールの一種) |
| color_intensity | 色の強さ |
| hue | 色合い |
| od280/od315_of_diluted_wines | ワインの希釈度合い |
| proline | プロリン (アミノ酸の一種) |
factor_analyzerによる因子分析
因子分析のためのPythonパッケージとしては主に次の2つがあるようです。
sklearn.decomposition.FactorAnalysisfactor_analyzer
factor_analyzerの方は回転なども扱えるようだったので、今回はこちらを使用します。
必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_wine
from factor_analyzer import FactorAnalyzer
データの読込み・前処理
scikit-learnが提供しているデータセットを読み込み、pandas DataFrameに格納します。
wine = load_wine()
X = pd.DataFrame(wine.data, columns=wine.feature_names)
print(X)
alcohol malic_acid ash alcalinity_of_ash magnesium total_phenols flavanoids nonflavanoid_phenols proanthocyanins color_intensity hue od280/od315_of_diluted_wines proline
0 14.23 1.71 2.43 15.6 127.0 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065.0
1 13.20 1.78 2.14 11.2 100.0 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050.0
2 13.16 2.36 2.67 18.6 101.0 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185.0
3 14.37 1.95 2.50 16.8 113.0 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480.0
4 13.24 2.59 2.87 21.0 118.0 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735.0
.. ... ... ... ... ... ... ... ... ... ... ... ... ...
173 13.71 5.65 2.45 20.5 95.0 1.68 0.61 0.52 1.06 7.70 0.64 1.74 740.0
174 13.40 3.91 2.48 23.0 102.0 1.80 0.75 0.43 1.41 7.30 0.70 1.56 750.0
175 13.27 4.28 2.26 20.0 120.0 1.59 0.69 0.43 1.35 10.20 0.59 1.56 835.0
176 13.17 2.59 2.37 20.0 120.0 1.65 0.68 0.53 1.46 9.30 0.60 1.62 840.0
177 14.13 4.10 2.74 24.5 96.0 2.05 0.76 0.56 1.35 9.20 0.61 1.60 560.0
[178 rows x 13 columns]
値の大小にばらつきがあるので正規化を行います。
X_stats = X.describe().transpose()
def norm(x):
return (x-X_stats['mean'])/X_stats['std']
X = norm(X)
因子分析
モデルを生成し、fit() メソッドでデータに適合させます。n_factors には仮定する因子の数 (default:3) を設定し、回転を与える場合には rotation を指定します。
fa = FactorAnalyzer(n_factors=3, rotation=None)
fa.fit(X)
計算された因子負荷行列は loadings_ 属性に格納されています。
fa.loadings_
array([[ 3.03695933e-01, 7.18459286e-01, -1.84135256e-01],
[-4.69444771e-01, 2.78685460e-01, 8.61921144e-02],
[-8.96586919e-04, 4.49071087e-01, 6.51789626e-01],
[-5.10072131e-01, -2.83591087e-02, 6.99150855e-01],
[ 2.63599880e-01, 3.49076632e-01, 9.10060413e-02],
[ 8.45207510e-01, 9.47272285e-02, 1.66562978e-01],
[ 9.38545127e-01, -1.21792372e-02, 1.90407577e-01],
[-5.80889756e-01, 4.43611005e-02, 1.38685529e-01],
[ 6.18386558e-01, 4.26912975e-02, 1.22035991e-01],
[-1.85667896e-01, 8.09678094e-01, -1.08117369e-01],
[ 5.98261734e-01, -3.88603476e-01, 5.02801023e-02],
[ 8.03486817e-01, -2.62017974e-01, 1.74507345e-01],
[ 6.02834445e-01, 5.48470217e-01, -1.24683648e-01]])
観測データを因子負荷行列を使って因子スコアに変換するには、引数にデータを与えて transform() を呼び出します。可視化のためにラベルも加えてみます。
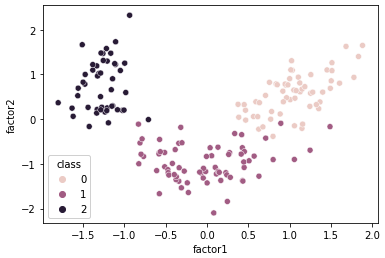
result_df = pd.DataFrame(fa.transform(X), columns=['factor1', 'factor2', 'factor3'])
result_df['class'] = wine.target
sns.scatterplot(x='factor1', y='factor2', hue='class', data=result_df)
factor1とfactor2を軸にとってみたところ、何となくクラス毎に別れている様子が確認できます。
各因子の考察
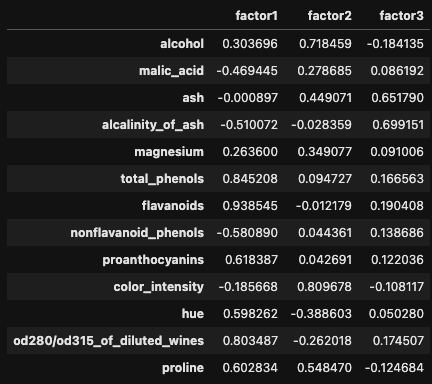
さて、因子分析によって導かれた各因子はどのような意味を持つでしょうか。見やすいように因子負荷行列をDataFrameに入れてみます。
loadings_df = pd.DataFrame(fa.loadings_, columns=['factor1', 'factor2', 'factor3'])
loadings_df.index = wine.feature_names
loadings_df
特徴量が専門的なので解釈が難しいですが、以下の傾向が見えるような気がします。
-
【factor1】 :
- (>0.6)
total_phenols,flavanoids,proanthocyanins,od280/od315_of_diluted_wines,proline - フェノール関係の特徴量が集まってるっぽい?
- (>0.6)
-
【factor2】 :
- (>0.6)
alcohol,color_intensity - アルコール度数と色の強さ (関連性はよく分からない)
- (>0.6)
-
【factor3】 :
- (>0.6)
ash,alcalinity_of_ash - 灰 (?) に関する特徴量
- (>0.6)
何らか共通の因子 (例えばfactor1) が存在して、それが原因で total_phenols や flavanoids といった値に影響を与えているのであれば、分析には意味があると言えます。化学に知見があればもう少し深い考察ができるかもしれません。
因子スコアによる分類
せっかくなので分類までやってみましょう。得られた因子スコアのデータとラベルを使ってSVMで分類してみます。
from sklearn.model_selection import KFold
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix
svc = SVC(C=1.0)
y = wine.target
# 5分割交差検証
kf = KFold(n_splits=5, random_state=0, shuffle=True)
# 予測結果格納用NumPy配列
y_pred = np.zeros((len(X),), dtype=float)
for train_idx, valid_idx in kf.split(X):
X_train, X_valid = X.iloc[train_idx], X.iloc[valid_idx]
y_train, y_valid = y[train_idx], y[valid_idx]
svc.fit(X_train, y_train)
y_pred[valid_idx] = svc.predict(X_valid)
acc = accuracy_score(y, y_pred)
# 0.9831460674157303
cnf = confusion_matrix(y, y_pred)
# [[58 1 0]
# [ 0 70 1]
# [ 0 1 47]]
次元数を落とした上でしっかり分類できています。めでたし!