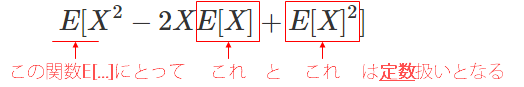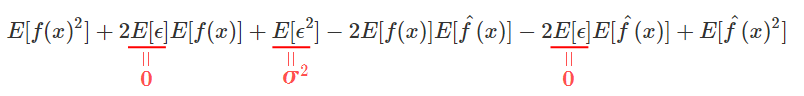機械学習にとって大切なことは全部MSE(平均二乗誤差)が教えてくれた

概要

機械学習の回帰問題において評価関数としてよく出てくる MSE(mean squared error,平均二乗誤差) とは一体何なのか。

山登りのように、ふもとから一歩ずつふみしめながら理解をすすめていく記録となります。

（必要な数式の導出過程も省略せず記録しました）

とうことで、さっそく山登り開始します

1合目：母集団・母平均

登り始める前に、準備運動。統計用語をおさらい

「日本人成人男性の平均身長調査」
を題材に、考えてみる。

選挙年齢が引き下げられたので　成人＝18歳以上　とすると　日本人のうち　成人　に該当するのは　約1億人。　そのうち男性が約半数なので、日本人成人男性は5000万人程度と考える。

母集団（ぼしゅうだん、population）

母集団とは、調査対象となる数値、属性等の源泉となる集合全体

平均身長調査で考えると、母集団とは対象者全員ということになる。

つまり母集団は5000万人（の日本人成人男性たち）

母平均（ぼへいきん,population mean)

母平均とは、母集団の平均のこと。平均は英語で mean その頭文字mに対応するギリシア文字$μ$(ミュー)を使うことが多いので、本稿でも$μ$をつかう。

さて、平均身長調査で考えると、母平均は以下のように計算できる。

母平均 μ=\frac{対象者全員ぶんの身長の総和}{5000万}

ちなみに、18歳以上の日本人成人男性の平均身長 $ μ=170.9cm $ だそう

2合目：大数の法則

大数の法則(たいすうのほうそく,Law of Large Numbers)

大数の法則とは、以下のような法則

「ある母集団から標本を抽出するとき、抽出する数が大きくなればなるほど、標本の平均は$μ$に近づく」
（$μ$は母集団の平均である母平均）

平均身長調査をしたら以下のようになったとする

• 母集団から10人の身長を無作為に抽出したら、その平均は166.5cmだった
  • 標本の大きさ 10 で、標本平均は 166.5
• 母集団から50人の身長を無作為に抽出したら、その平均は169.2cmだった
  • 標本の大きさ 50 で、標本平均は 169.2
• 母集団から500人の身長を無作為に抽出したら、その平均は170.5cmだった
  • 標本の大きさ 500 で、標本平均は 170.5

多くの標本を抽出すると、その平均が 母平均 $ μ=170.9cm $ に近づいていくことがわかる。

このように母集団から抽出した標本の平均のことを標本平均という

3合目：確率変数

確率変数(かくりつへんすう、 random variable)

確率変数とは「どのような値をとるかが、ある確率によって決まる変数」

確率変数には$ X $がよく使われる。

平均身長調査で考える。

任意に抽出した人の身長を確率変数$ X $と考えると、
数学的には、「確率変数$ X $は　対象となる人→その身長　という関数」を意味する。

身長180cm以上190cm以下の確率、150cm未満の確率など、
確率変数は確率分布に対応し、妥当にあり得る範囲の確率を計算できる。
(wikipediaより)

平均身長調査で母集団から標本を抽出したとき、抽出した身長データ $ \mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_n $ (cm)は確率変数$ \mathbf{X}_1,\mathbf{X}_2,...\mathbf{X}_n $の実現値と考えることができる。$n$は標本の大きさという。

実現値(観測値)・・・実際の試行の結果として観察された値

4合目：期待値と平均

期待値(きたいち、expected value)

期待値とは「確率変数のすべての値に確率の重みをつけた加重平均」のこと

確率変数$X$の期待値は、$E(X)$で表すことが多い。

平均身長調査で考える。

任意に抽出した人の身長を確率変数$ X $としたとき、
母集団から標本を抽出したとき、抽出した身長データ $ \mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_n $ (cm)のそれぞれの発生確率（その身長の人がどのくらいの割合いるのか）を$\mathbf{p}_1,\mathbf{p}_2,...\mathbf{p}_n $とすると、その期待値$E(X)$は以下のように計算¹する。

E(X) = \sum_{i=1}^{n}\mathbf{x}_i\mathbf{p}_i

期待値の性質①「和の期待値は期待値の和」

和の期待値は期待値の和となる性質がある（期待値の線形性）

E[X+Y]=E[X]+E[Y]

期待値の性質②「定数の期待値は定数」

E[C]=C

期待値の性質③「(定数＋確率変数)の期待値は、定数＋確率変数の期待値」

E[C+x]=C+E[X]

期待値の性質④「(定数ｘ確率変数)の期待値は、定数ｘ確率変数の期待値」

E[CX]=CE[X]

期待値と平均の違い

期待値と平均の違いは平均の定義を見て考える必要がある。

確率変数の平均

確率変数$X$の平均は確率変数すべての値に確率の重みを付けた加重平均であり、これは期待値のことを示す

E(X) = \sum_{i=1}^{n}\mathbf{x}_i\mathbf{p}_i

母集団の平均(期待値)を$μ$とすれば、

μ = E(X) = \sum_{i=1}^{n}\mathbf{x}_i\mathbf{p}_i

となる

標本平均

以下の平均身長調査の例を再度考える

• 母集団から10人の身長を無作為に抽出したら、その平均は166.5cmだった
  • 標本の大きさ 10 で、標本平均は 166.5

母集団から10件の標本を抽出したら以下のようなデータが取得できたとする

x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	平均
160	166	162	163	172	169	166	168	172	167	166.5

この標本の平均は、母集団から標本を抽出したとき、抽出した身長データ $ \mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_n $ (cm)としたとき、抽出した身長データの総和を、抽出した個数$n$で割ったものとなる

\begin{align}
 \frac{x1+x2+x3+x4+x5+x6+x7+x8+x9+x10}{n}&=\\
\\
 \frac{160+166+162+163+172+169+166+168+172+167}{10} &= 166.5
\end{align}

つまり平均$E[X]$を式で表すと以下のようになる

E(X) = \frac{\sum_{i=1}^{n}\mathbf{x}_i}{n}

平均を表す場合はよく変数の頭にバーをつけて$ \bar{x}$のようにするので以下のようにした

標本平均 \bar{x} = E(X) = \frac{\sum_{i=1}^{n}\mathbf{x}_i}{n}

ここで、標本の大きさ**$n$** をどんどん大きくしていって平均身長調査の母数5000万人に近づけていったらどうなるか。

大数の法則を思い出すと、

「ある母集団から標本を抽出するとき、抽出する数が大きくなればなるほど、標本の平均は$μ$に近づく」
（$μ$は母集団の平均である母平均）

であるので、
標本の大きさ$n$を大きくしていくと、標本平均 $\bar{x}$は母平均μに限りなく近づく

つまり、5000万人ぶんの標本（身長データ）を集めることができれば、その標本平均は母平均と一致する。母平均とは母集団の平均＝期待値なので、この場合、標本平均＝期待値となる。

まとめると、

• 確率変数$X$の平均は確率変数すべての値に確率の重みを付けた加重平均であり、これを期待値とも呼ぶ

μ = E(X) = \sum_{i=1}^{n}\mathbf{x}_i\mathbf{p}_i

• 標本平均$\bar{x}$は標本の大きさ$n$が増えるほど、大数の法則により母集団の平均$μ$(期待値)に限りなく近づく

\begin{align}
 \bar{x} &= E(X) = \frac{\sum_{i=1}^{n}\mathbf{x}_i}{n}\\
&n → ∞のとき μ =  \bar{x}

\end{align}

確率論的視点と統計学的視点

ここまでで、だんだん気づいてきたとおもうが、いままでのトピックは一定の確率をもって変数が決まる確率論的見方と、母集団から標本を抽出して母集団の推測しようとする統計学的見方と両方の視点であえてごちゃっと見てきた。

どちらかというと、目に見えづらい確率論的見方よりも、標本を集めて統計的処理をしていく統計学的視点のほうがピンと来る気もするが機械学習の理論を学ぶ上ではどちらの見方も重要だと考える。

5合目：分散

分散(ぶんさん、variance)

分散は英語よみそのままでバリアンスともいう。

分散とは「確率変数値が全体として**「平均」からどれだけ散らばっているか**を表す特性値」のこと。

分散は平均からの散らばり具合を示し、0に近いほど散らばりが少ない（まとまっている）、大きいほど散らばっている（ばらばらになっている）

分散はVarianceなので、分散を関数的に表すとき$ V[X] $や $VAR[X]$、$Var[X]$などが好んで使われる。

さて、確率論的見方と統計学的見方の両方の定義をみていく。

確率変数の分散

まず、確率論的見方から。

確率変数$X$の期待値を$E[X]$とすると、分散$V[X]$は以下のようになる

V[X]=E[(X-E[X])^2]

つまり、確率変数$X$ からその期待値$E(X)$を引いた値の二乗の期待値となる。

上の式は、あとでMSE(平均二乗誤差）を計算するときに展開するので覚えておくとよい。

標本の分散

次は統計学的見方で分散を見る

ある母集団から抽出した標本の分散を標本分散という

$\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_n $ からなる標本があり、その平均を$\bar{x}$としたときこの標本の分散は以下の数式で計算される

s^2=\frac{1}{n}\sum_{i=1}^{n}(\mathbf{x}_i-\bar{\mathbf{x}})^2 \\

$s$は標準偏差を示す。

この式のとおり、標準偏差を二乗したものを分散というので、$標準偏差=\sqrt{分散}$となる

\begin{align}
標準偏差 &= \sqrt{分散}\\
s &=  \sqrt{\frac{1}{n}\sum_{i=1}^{n}(\mathbf{x}_i-\bar{\mathbf{x}})^2}
\end{align}

母集団の分散

母集団の分散(母分散）も、計算式は標本の分散と同じだが、分散の記号として$\sigma^2$がよく使われる。
$\bar{\mu}$は母集団の平均(母平均)、$\sigma$は母集団の標準偏差。

\sigma^2=\frac{1}{n}\sum_{i=1}^{n}(\mathbf{x}_i-\bar{\mu})^2 \\

6合目：分散の式の展開

ひきつづき、分散をみていく。
分散というのは、統計学では最も重要な概念ともいわれているし、今回の目的でもあるMSE(平均二乗誤差)を考える上でも非常に重要なので丁寧にみていく。

分散の式を展開する

分散の式は以下のように展開可能である

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2]\\
&=E[X^2]-E[X]^2
\end{align}

計算過程がよく飛ばされるので、今回は丁寧にみていく

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2] \tag{1}\\
&=E[X^2-2XE[X]+E[X]^2] \tag{2}\\
\end{align}

さて、ここで(2)の式に注目すると、一番外側の$E[　]$にとって、その内側にいる$E[X]$と$E[X]^2$は定数扱いとなる。

この状態で、期待値の性質①をつかって式(2)を分解すると式(3)のようになり、

期待値の性質①「和の期待値は期待値の和」

E[X+Y]=E[X]+E[Y]

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2] \tag{1}\\
&=E[X^2-2XE[X]+E[X]^2] \tag{2}\\
&=E[X^2]-E[2XE[X]]+E[E[X]^2] \tag{3}\\
\end{align}

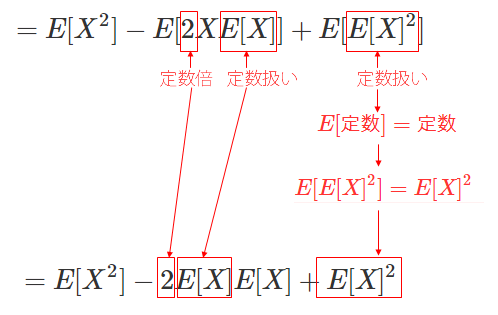
さらに、外側の$E[　]$の内側にいる$E[X]$と$E[X]^2$は定数扱いとなるので、式(4)のようにできる

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2] \tag{1}\\
&=E[X^2-2XE[X]+E[X]^2] \tag{2}\\
&=E[X^2]-E[2XE[X]]+E[E[X]^2] \tag{3}\\
&=E[X^2]-2E[X]E[X]+E[X]^2 \tag{4}\\
\end{align}

式(3)から式(4)の展開をもう少し詳しくみると以下のようになる。

$E[2XE[X]]$の2は定数、また$E[X]$も外側の$E[　]$にとっては定数なので期待値の性質④「(定数ｘ確率変数)の期待値は、定数ｘ確率変数の期待値」より、外だしして$2E[X]E[X]$となる。

次の$E[E[X]^2]$は、内側の$E[X]^2$は外側の$E[　]$にとって定数となるので 期待値の性質②「定数の期待値は定数」より$E[定数]=定数$と考えることができるので$E[E[X]^2]=E[X]^2$となる。

さて、残り展開を式(5)と式(6)のようにして以下のようになった

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2] \tag{1}\\
&=E[X^2-2XE[X]+E[X]^2] \tag{2}\\
&=E[X^2]-E[2XE[X]]+E[E[X]^2] \tag{3}\\
&=E[X^2]-2E[X]E[X]+E[X]^2 \tag{4}\\
&=E[X^2]-2E[X]^2+E[X]^2 \tag{5}\\
&=E[X^2]-E[X]^2 \tag{6}\\
\end{align}

これにより、さきほど求めたかった以下の関係を導出できた

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2]\\
&=E[X^2]-E[X]^2
\end{align}

分散の計算過程を今回は確率変数$X$の例で計算したが、これは母分散や標本の分散の計算式でも同じ事がいえる。

\begin{align}
s^2&=\frac{1}{n}\sum_{i=1}^{n}(\mathbf{x}_i-\bar{\mathbf{x}})^2 \\
&=\frac{1}{n}\sum_{i=1}^{n}\mathbf{x}_i^2-\bar{\mathbf{x}}^2 \\
\end{align}

7合目：MSE(平均二乗誤差,mean squared error)の定義

ようやく7合目まできた
いよいよMSEの定義をひもといていく。

学習モデルと真のモデルとMSE

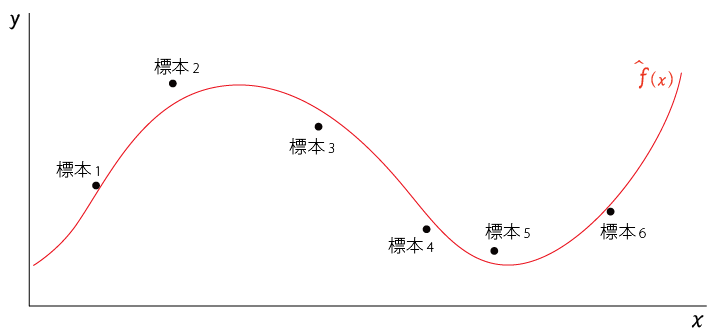
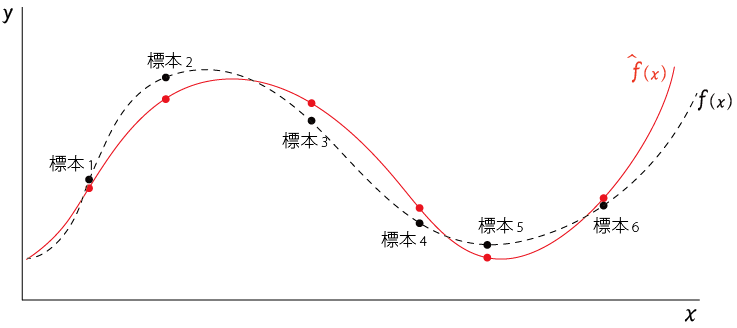
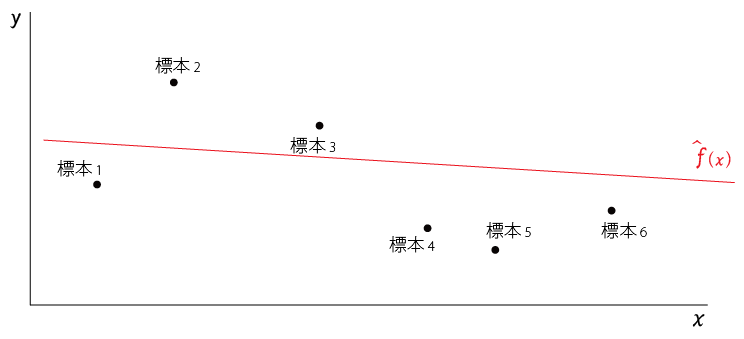
式の意味や定義を理解しやすくするために、以下のような状況を設定する

ある母集団から無作為に$標本_1,標本_2,,,標本_n$を抽出する

この標本に$x$、$y$の変数があるとき、それをプロットすると以下のようになったとする

この標本を入力として機械学習をさせて得られた学習モデルを$\hat{f}(x)$とする。

$\hat{f}(x)$は以下の赤線のようになる

$\hat{y}$を学習モデルの予測値とすると、以下のようにあらわすことができる

\hat{y}=\hat{f}(x)

このように、この学習モデル$\hat{f}(x)$をつかえば$x$から$y$を予測することができる

ちなみに、$\hat{y}$や$\hat{f}(x)$の上に$\hat{}$がついているが、一般に予測や推定を示す関数や値にはハット($\hat{}$)をつけて表現することが多いので覚えておく

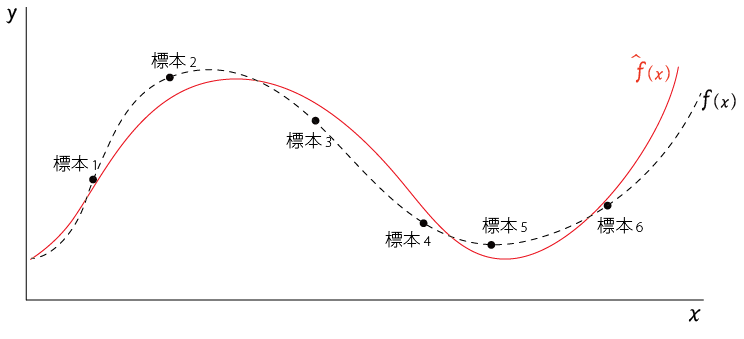
学習によって得られた学習モデル$\hat{f}(x)$は$標本_1,標本_2,,,標本_n$の近似をしている関数 と考えるとわかりやすい

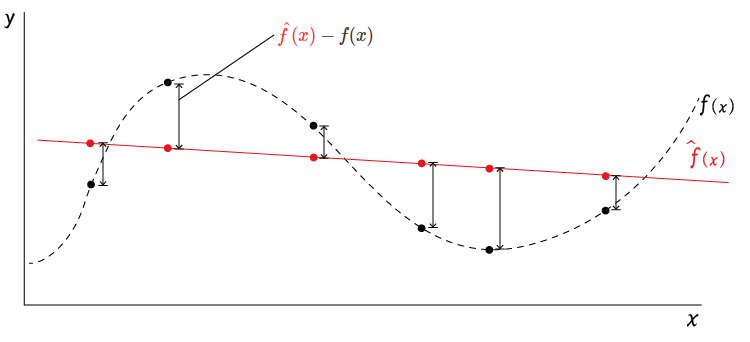
ところで、学習モデル$\hat{f}(x)$は観測済みの標本から作られているのに対して、真のモデル$f(x)$は直接観測することはできない。

真のモデルを$f(x)$とすると、その値$y$（真の値）との関係は以下のようになる

y=f(x)+\epsilon

$\epsilon$(イプシロン)は真のモデル自身がもつノイズ。これは真のモデルにどうしても内在するもので、コントロール不可能なもの。

$\epsilon$は平均が0、分散が$\sigma^2$の分布を持つ

真のモデル$f(x)$のイメージは以下の点線のような感じになる
（真のモデルは外部から観測できないので、ほんとうは描けない）

学習モデルが予測した$\hat{y}=\hat{f}(x)$と、真のモデル$f(x)$とノイズ$\epsilon$(平均:$0$、分散:$\sigma^2$)から計算される真の値$y=f(x)+\epsilon$の差が小さいほど「学習モデルは本当の値をよく近似できている」といえるので、この差を小さくするのが学習の目的となる。

\begin{align}
真の値・・・y&=f(x)+\epsilon\\
予測値・・・\hat{y}&=\hat{f}(x)\\
\end{align}

学習モデル$\hat{f}(x)$の**MSE(平均二乗誤差)**の式は以下のようになる

\begin{align}
MSE[\hat{f}(x)]&=E[(y-\hat{f}(x))^2]\\
&=E[((f(x)+\epsilon)-\hat{f}(x))^2]\\
\\
&\epsilon・・・平均:0,分散:\sigma^2
\end{align}

8合目：汎化誤差と訓練誤差（経験誤差）

訓練誤差(Training error)

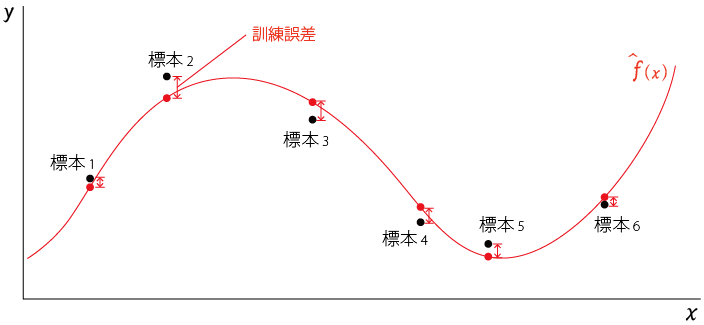
ところで、いままでみてきた機械学習は、ある母集団から無作為に抽出した$標本_1,標本_2,,,標本_n$をつかって行っている

その機械学習の結果得られた学習モデルは当然ながら入力となった標本を参考にしてできたものとなる

学習モデルが予測した値を以下のように赤丸●でプロットした
また、実際の値（真の値）は標本の黒丸●でプロットした

この、黒丸●と赤丸●の差が訓練誤差となる

訓練誤差とは、「学習につかった値と、学習モデルの予測した値の誤差」のことを指す

ここでいえば、標本を学習につかっているので、観測済みの標本と予測値の誤差となる

訓練誤差は、経験誤差、学習誤差、経験損失ともよぶ。

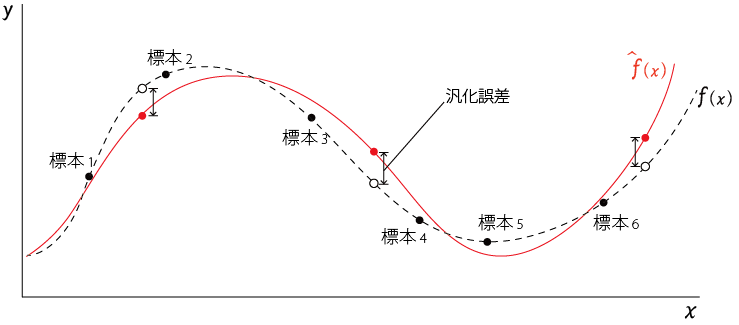
汎化誤差(Test Error)

それに対して、
汎化誤差とは「真のモデルと学習モデルの誤差」を指す。つまり、まだ観測されていない値（以下の図の○のようなデータ）を含む真のモデルと学習モデルの誤差。

前節で以下のように書いたが、より詳しくいえば

**学習モデル$\hat{f}(x)$と真のモデル$f(x)$**の差が小さいほど学習モデルは本当の値をよく近似できているといえるので、この差を小さくするのが学習の目的となる。

「学習の目的は学習モデルと真のモデルの差つまり汎化誤差が小さくなるようにする」ことが重要といえる。

ということで、機械学習の目標は汎化(generalization)性能の獲得、つまり汎化誤差の最小化といえる

汎化誤差は、テスト誤差、期待損失ともいう。

9合目：バイアスとバリアンスのトレードオフとMSE

MSEの計算式を展開する

7合目を思い出す

学習モデルが予測した$y=\hat{f}(x)$と真のモデル$f(x)$とノイズ$\epsilon$(平均:$0$、分散:$\sigma^2$)から来る真の値$\hat{y}=f(x)+\epsilon$の差が小さいほど学習モデルは本当の値をよく近似できているといえるので、この差を小さくするのが学習の目的となる。

\begin{align}
真の値・・・y&=f(x)+\epsilon\\
予測値・・・\hat{y}&=\hat{f}(x)\\
\end{align}

学習モデル$\hat{f}(x)$の**MSE(平均二乗誤差)**の式は以下のようになる

\begin{align}
MSE[\hat{f}(x)]&=E[(y-\hat{f}(x))^2]\\
&=E[((f(x)+\epsilon)-\hat{f}(x))^2]\\
\\
&\epsilon・・・平均:0,分散:\sigma^2
\end{align}

バイアスとバリアンスの話をするために、重要となるのが、以下の式(1)となる。

\begin{align}

MSE[\hat{f}(x)]&=E[(y-\hat{f}(x))^2]\\
&=E[((f(x)+\epsilon)-\hat{f(x)})^2] \\
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2  \tag{1}\\
\end{align}

ここでは、MSEの式を展開して式(1)$MSE[\hat{f}(x)]=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2$を導出していく。

$MSE[\hat{f}(x)]$

\begin{align}
&=E[((f(x)+\epsilon)-\hat{f(x)})^2] \\
&=E[(f(x)+\epsilon)^2-2(f(x)+\epsilon)\hat{f}(x)+\hat{f}(x)^2] \tag{2}\\
&=E[f(x)^2+2\epsilon f(x)+\epsilon^2-2f(x)\hat{f}(x)-2\epsilon\hat{f}(x)+\hat{f}(x)^2] \tag{3}\\
&=E[f(x)^2]+E[2\epsilon f(x)]+E[\epsilon^2]-E[2f(x)\hat{f}(x)]-E[2\epsilon \hat{f}(x)]+E[\hat{f}(x)^2] \tag{4}\\
&=E[f(x)^2]+2E[\epsilon]E[f(x)]+E[\epsilon^2]-2E[f(x)]E[\hat{f}(x)]-2E[\epsilon]E[\hat{f}(x)]+E[\hat{f}(x)^2] \tag{5}\\
\end{align}

式(5)について、各項にでてくる$\epsilon$について考察する。

まず、$E[\epsilon]$について。$\epsilon$は平均が0のノイズ成分なので、$E[\epsilon]=0$となる。

E[\epsilon]=0  \tag{6}\\

また、6合目でみた以下の分散$V[X]$の式より、

\begin{align}
V[X]&=E[(X-E(X))^2]\\
&=E[X^2]-E[X]^2
\end{align}

であるので、これを変形すると

E[X^2]=V[X]+E[X]^2

ここに$\epsilon$を代入すると

E[\epsilon^2]=V[\epsilon]+E[\epsilon]^2  \tag{7}\\

となる。$\epsilon$の定義より分散$V[\epsilon]=\sigma^2$、$E[\epsilon]=0$であるので式(7)は

\begin{align}
E[\epsilon^2]&=V[\epsilon]+E[\epsilon]^2  \\
&= \sigma^2+0^2  \\
&=\sigma^2
\end{align}

となり、

E[\epsilon^2]=\sigma^2\tag{8}\\

式(6)(8)より、$E[\epsilon]=0$、$E[\epsilon^2]=\sigma^2$であるので、式(5)は

となるので

$MSE[\hat{f}(x)]$

\begin{align}
&=E[f(x)^2]+2E[\epsilon]E[f(x)]+E[\epsilon^2]-2E[f(x)]E[\hat{f}(x)]-2E[\epsilon]E[\hat{f}(x)]+E[\hat{f}(x)^2]\\
&=E[f(x)^2]+\sigma^2-2E[f(x)]E[\hat{f}(x)]+E[\hat{f}(x)^2]\tag{9}\\
\end{align}

これまでと同様、$\hat{f}(x)$の関数において$E[f(x)]$の$f(x)$は定数であるので

\begin{align}

MSE[\hat{f}(x)]&=f(x)^2+\sigma^2-2f(x)E[\hat{f}(x)]+E[\hat{f}(x)^2]\tag{10}\\
\end{align}

式(10)の各項の順番を入れ替え

\begin{align}

MSE[\hat{f}(x)]
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2\tag{11}\\
\end{align}

以下のように式(1)を導出することができた

\begin{align}

MSE[\hat{f}(x)]
&=E[((f(x)+\epsilon)-\hat{f(x)})^2] \\
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2　 \tag{1}\\
\end{align}

この結果を覚えておきつつ、バイアスをみていく

バイアス(bias)とは

バイアスとは、偏りのことを意味する。

学習によって得られた学習モデルを$\hat{f}(x)$、直接観測できない真のモデルを$f(x)$とすると
$\hat{f}(x)$のバイアス$Bias(\hat{f}(x))$は以下のようになる

Bias[\hat{f}(x)]=E[\hat{f}(x)-f(x)]

バイアスは「学習モデルによる予測値と真のモデルの差の期待値」なので、差が大きい＝バイアスが高い(high biasという) とモデルの精度がわるい

訓練データをつかって、機械学習したときにバイアスが高くなってしまうようなモデルだと、いくらたくさん訓練データを入力してもモデルの精度が悪いままとなる。また、当然テストデータ（学習済みのモデルの性能を評価するためのデータ）をつかっても、モデルの精度が悪い。

なので、なるべくバイアスが低くなるよう学習させたい

バリアンス(variance,分散)とは

バリアンスは分散のこと。分散は5合目で見てきたとおりで、

分散とは「確率変数値が全体として「平均」からどれだけ散らばっているかを表す特性値」
となる。

\begin{align}
V[X]=\sigma^2&=E[(X-E(X))^2]\\
&=E[X^2]-E[X]^2
\end{align}

学習によって得られた学習モデルを$\hat{f}(x)$としたとき、$\hat{f}(x)$の分散は

\begin{align}
V[\hat{f}(x)]&=E[(\hat{f}(x)-E(\hat{f}(x)))^2]\\
&=E[\hat{f}(x)^2]-E[\hat{f}(x)]^2
\end{align}

となる。

バリアンスとは、平均からの散らばり具合だが、ここでいう平均とは、学習モデルが予測した値の平均。個々の予測値と、予測値の平均が離れている状態はバリアンスが高い（high variance)という。

モデルを複雑にしていくと、よく訓練データにフィットするようになる(バイアスが低くなる)が
訓練データにフィットしすぎ(overfit)て、テストデータにはフィットしなくなる。
こういう状況はバリアンスが高い(high variance)状態となる。

このようにバリアンスはモデルが複雑になるほど高くなりモデルが不安定になる

MSEはバイアス(bias)とバリアンス(variance)の成分でできていることを確認する

バイアスとバリアンスの特徴を軽く把握したところで、MSEとバイアス$Bias[\hat{f}(x)]$とバリアンス$V[\hat{f}(x)]$の関係をみてみる。

結論からいうと、

MSE[\hat{f}(x)]=V[\hat{f}(x)]+Bias[\hat{f}(x)]^2+\sigma^2

となる。

これを式で確かめてみる

バリアンス＝分散$V[\hat{f}(x)]$は以下の通り、

\begin{align}
V[\hat{f}(x)]
&=E[\hat{f}(x)^2]-E[\hat{f}(x)]^2
\end{align}

バイアス$Bias[\hat{f}(x)]$の二乗$Bias[\hat{f}(x)]^2$を計算すると以下の通り

\begin{align}
Bias[\hat{f}(x)]&=E[\hat{f}(x)-f(x)]\\
\\
Bias[\hat{f}(x)]^2&=E[\hat{f}(x)-f(x)]^2\\
&=E[\hat{f}(x)]^2-2f(x)E[\hat{f}(x)]+f(x)^2
\end{align}

であるので、

\begin{align}
V[\hat{f}(x)]+Bias[\hat{f}(x)]^2&=(E[\hat{f}(x)^2]-E[\hat{f}(x)]^2) + (E[\hat{f}(x)]^2-2f(x)E[\hat{f}(x)]+f(x)^2)\\
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2\\
\\
MSE[\hat{f}(x)]
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2 \\
\\
V[\hat{f}(x)]+Bias[\hat{f}(x)]^2+\sigma^2 &=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2 
\end{align}

これにより、以下のように、MSE(平均二乗誤差)は「$V$(バリアンス=分散)」と「$Bias^2$(バイアスの二乗)」と「真の値に含まれる誤差の分散$\sigma^2$」によって構成される値であることが確認できた。

\begin{align}
MSE[\hat{f}(x)]
&=V[\hat{f}(x)]+Bias[\hat{f}(x)]^2+\sigma^2\\
&=E[\hat{f}(x)^2]-2f(x)E[\hat{f}(x)]+f(x)^2+\sigma^2 \\
\end{align}

バイアス(bias)とバリアンス(variance)のトレードオフ

バイアスが高い(high bias)とき

以下は標本に対して直線で近似した学習モデルとなる（――の線）

バイアス$Bias[\hat{f}(x)]$は以下のように、学習モデル$\hat{f}(x)$と真のモデル$f(x)$の差から計算される

\begin{align}
Bias[\hat{f}(x)]&=E[\hat{f}(x)-f(x)]\\
\end{align}

学習モデル$\hat{f}(x)$と真のモデル$f(x)$の差$\hat{f}(x)-f(x)$を図示すると以下のような感じ

上のように、「学習モデルと真のモデルの差$\hat{f}(x)-f(x)$が大きい」＝「バイアスが高い」＝「精度の悪いモデルしかできない」

こういう状態を 未学習 underfit という。

バイアスを低く(low bias)する

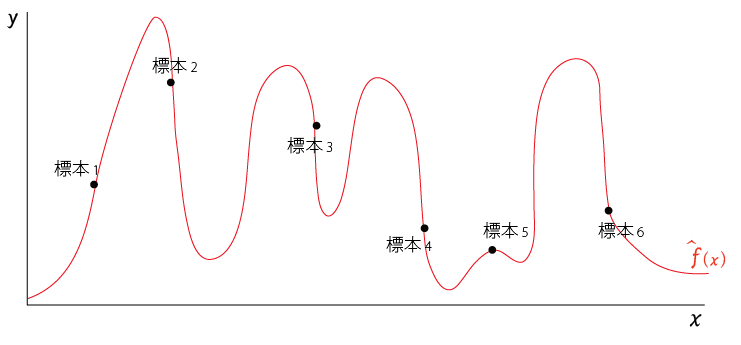
では、反対に学習モデルと真のモデルの差$\hat{f}(x)-f(x)$を徹底的に小さくするように学習させたとする。

学習モデルでは直線ではなくもっと複雑な関数で近似してみたら
以下のようになったとする。

訓練データ（標本）に見事に一致している学習モデルが出来た

この状態は「学習モデルと標本の差が非常に小さくなるように学習できている」＝「バイアスは非常に低い」を達成できているが、今度は訓練データ（標本）に学習モデルをピッタリ一致させたいが為に学習モデルがだいぶ複雑化してしまっているようなパターンとなる

このように複雑なモデルをつくってしまうと過剰にフィットして「バリアンス（分散）が高い状態」になりやすい

このバリアンスが高い状態を 過学習 overfitという。

トレードオフ関係

トレードオフ関係とは、こちらを良くしようとすると、あちらが悪くなる　という関係。

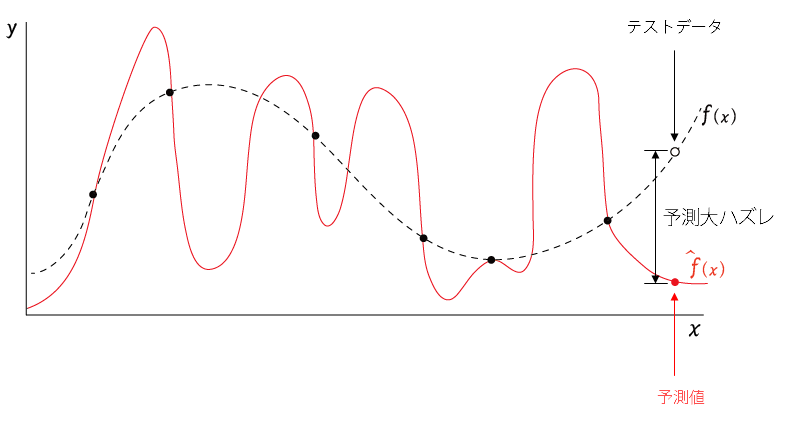
過学習(overfit)がおきていると、訓練データに対してはよくフィットするが、
訓練データ外のデータ、たとえばテストデータがくると下図のように予測がハズれて、精度が落ちてしまうという現象がおこりやすい。

(以下の○が訓練データ外のデータ）

つまり、
バイアスを低くしようとすると、バリアンスが高く(overfitするリスク)なる
というトレードオフの関係が存在するので、両者を良い感じに調整するのが学習モデルをつくる上でのポイントとなる。

上でみたように、

\begin{align}
MSE[\hat{f}(x)]
&=V[\hat{f}(x)]+Bias[\hat{f}(x)]^2+\sigma^2\\
\end{align}

の関係があるので、
**MSE(平均二乗誤差)**を小さくする（バイアスもバリアンスも小さくなればMSEも小さくなる）という方針は、良い学習モデルを作るということになる。

10合目：母数の推定

MSE登山も、だいぶ高いところまで上ってきて、ようやく山頂が見えてきたような

MSEの計算(予測値)

学習モデル（もう学習済みのモデル）で予測（回帰）を行ったとき、MSEの計算をする方法を再確認しておく。

つまり訓練誤差ではなく汎化誤差の計算をする場合、

• 学習モデルを$\hat{y}=\hat{f}(x)$、
• テストデータ(学習に使ってないデータ)が$N$個
• テストデータの値を順番に　$y_0,y_1,y_2,,,y_{N-1}$　とする
• 学習モデルによって予測された予測値を　$\hat{y}_0,\hat{y}_1,\hat{y}_2,,,\hat{y}_{N-1}$　

とするとき、MSEは以下のように計算できる。

MSE[\hat{\mathbf{y}}] = \frac{1}{N}\sum_{i=0}^{N-1} (\mathbf{y}_i - \hat{\mathbf{y}}_i)^2\\

MSEの計算(母数推定)

これまでは、標本にある具体的な変数に関して変数$X$と変数$Y$の関係を機械学習によってモデル化する視点でMSEをみてきた。

これと同様に、母数の推定においてもこれまでみてきたMSEの計算式と同様の考え方ができるので少しふれておく。

ちなみに、機械学習のプログラミングをする上では、9合目までの知識でそんなに困らない気がするので、ここはさらっと。

MSEの解説を調べたりすると、けっこうな確率で母数の推定の話($\theta$や$\hat{\theta}$がドヤ顔で使われた数式)がでてくるので、そういうときに困惑しない程度に。

母数(parameter)とは

母数は英語だとパラメータ(parameter)

母数とは、確率変数の確率分布を特徴付ける数である。たとえば、ポアソン分布では平均 λ, 正規分布では平均 μ および分散 σ2 がこれにあたる

wikipediaより

母数は分母という意味ではないし、全体の数という意味でもないので注意。
（「パラメータ(parameter)」という英語表現のほうが意味をつかみやすい）

推定量(Estimator)とは

推定量（すいていりょう）とは、現実に測定された標本データをもとに、確率分布の母数（パラメータ、現実には測定できない）として推定した数量（英語：Estimate）、もしくはそれをデータの関数として表す推定関数（すいていかんすう：Estimator）のことをいう。

wikipediaより

母数(parameter)の推定

母数には良く$\theta$がつかわれ、推定量は良く$\hat{\theta}$が使われる。どちらも単なる記号なので難しいことはない。

推定量のMSE(平均二乗誤差)は以下の式であらわされる

MSE[\hat{\theta}]=E[(\hat{\theta}-\theta)^2]

また、

MSE[\hat{\theta}]=V[\hat{\theta}]+(Bias[\hat{\theta}])^2

の関係が成り立つ。

いままでみてきたものと似ているし、導出の過程もほぼ同じ、なので、このくらいで。

PredictorとEstimator

学習モデルによって、数値や分類を予測(回帰)するときの予測器をPredictor、
母数の推定量（ or 推定するための関数）をEstimator という。

英語文献などでは、明確に分けて書いてあるのでおぼえておく。

ちなみに、このあたりの定義については論争もある模様。参考程度に。

山頂へ（まとめ）

MSEについて山登りをして、ようやく山頂についたかな、という感じです。

基本的な確率・統計のキーワードや大数の法則からからはじめて、確率、期待値・平均とすすめ5合目までは統計学でも特に重要な概念といわれる分散を理解するためのステップでした。

6合目から先はMSE(平均二乗誤差)の性質を理解するためのステップでバイアスとバリアンスという成分でできていることを理解できました。

10合目の入り口ではMSEの計算法や母数の推定についての考え方を簡単に整理しました。

MSEを調べていくと、機械学習に必要な確率・統計の知識が自然と学習できてなかなかお得感がありました。

MSEの山頂に登った気でいますが、
その先にまだまだ、奥深い世界が広がっているので歩みをとめず、先に進んでいきたいと思います。

最後までお読みいただき、ありがとうございました

参考にした資料・文献等

(順不同)

• はじめてのパターン認識
• 東京大学データサイエンティスト養成講座
• 計量経済学の第一歩
• 統計学からの計量経済学入門
• wikipedia(日本語版より英語版のほうが詳しい)
• http://www.deeplearningbook.org/

1. この数式は離散型変数（サイコロの目のように1,2,3と飛び飛びの値をとるもの）のためのもので、実際に身長は連続型変数となるが、後にMSEを考察するときにこちらのほうがわかりやすいので、$\sum_{i=1}^{n}\mathbf{x}_i\mathbf{p}_i$を期待値計算式として用いる ↩