はじめに
今回の記事は前回の続きになります。
よろしければ以下の記事もご覧ください。
[機械学習]決定木について分かりやすくまとめてみる①~理論編~
分類木の実装
それでは分類木を実装しています。
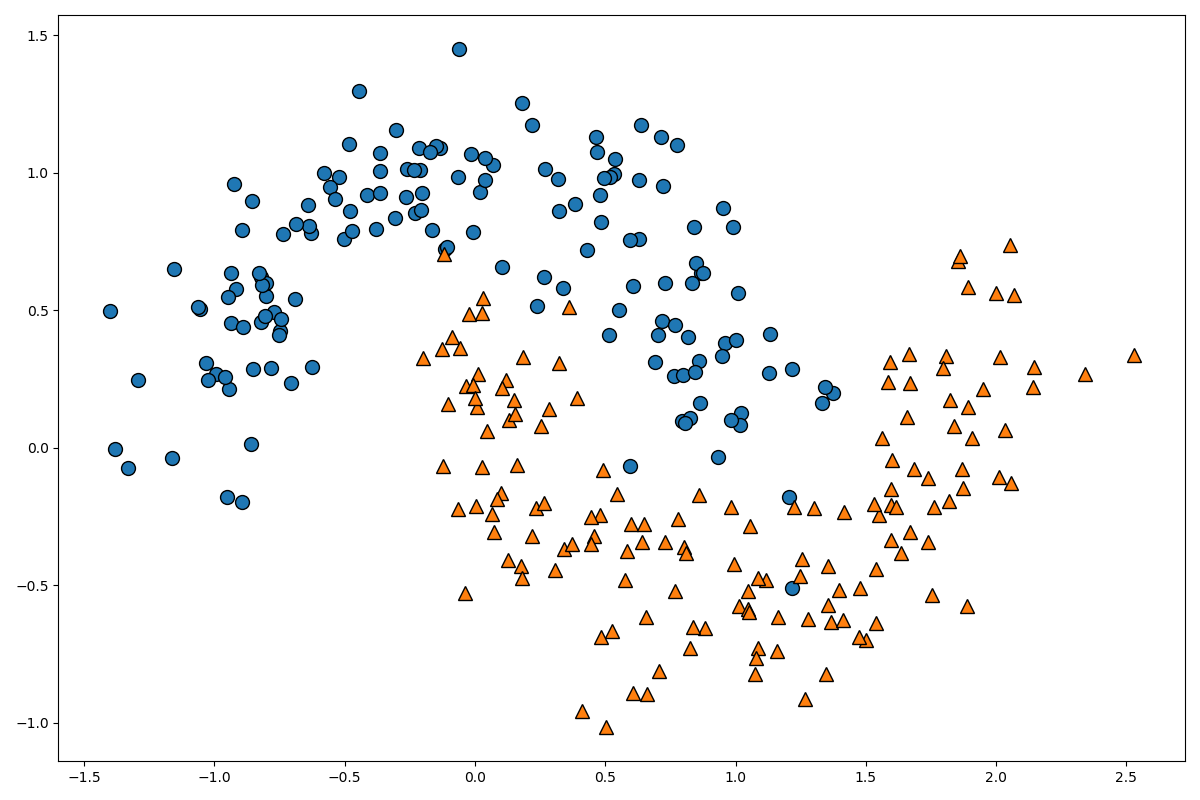
まず、分類するデータを作成します。
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from matplotlib.colors import ListedColormap
import graphviz
moons = make_moons(n_samples=300, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0, stratify=Y)
plt.figure(figsize=(12, 8))
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.show()
このデータを分類するモデルを作成していきます。
以下のコードです。
clf_model = DecisionTreeClassifier(max_depth=3)
clf_model.fit(X_train, Y_train)
print(clf_model.score(X_test, Y_test))
0.8933333333333333
そこそこの精度がでましたね。
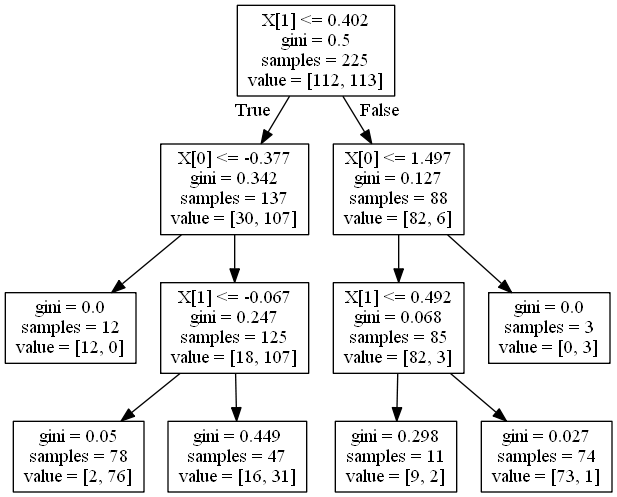
この分類木のモデルを可視化してみましょう。以下のコードです。
dot_data = export_graphviz(clf_model)
graph = graphviz.Source(dot_data)
graph.render('moon-tree', format='png')
graphvizを用いた可視化については、こちらの記事を参考にしてください。
このように、決定木はモデルの解釈性が非常に高いです。今回のモデルではmax_depth=3としたため、深さが3のモデルになっています。
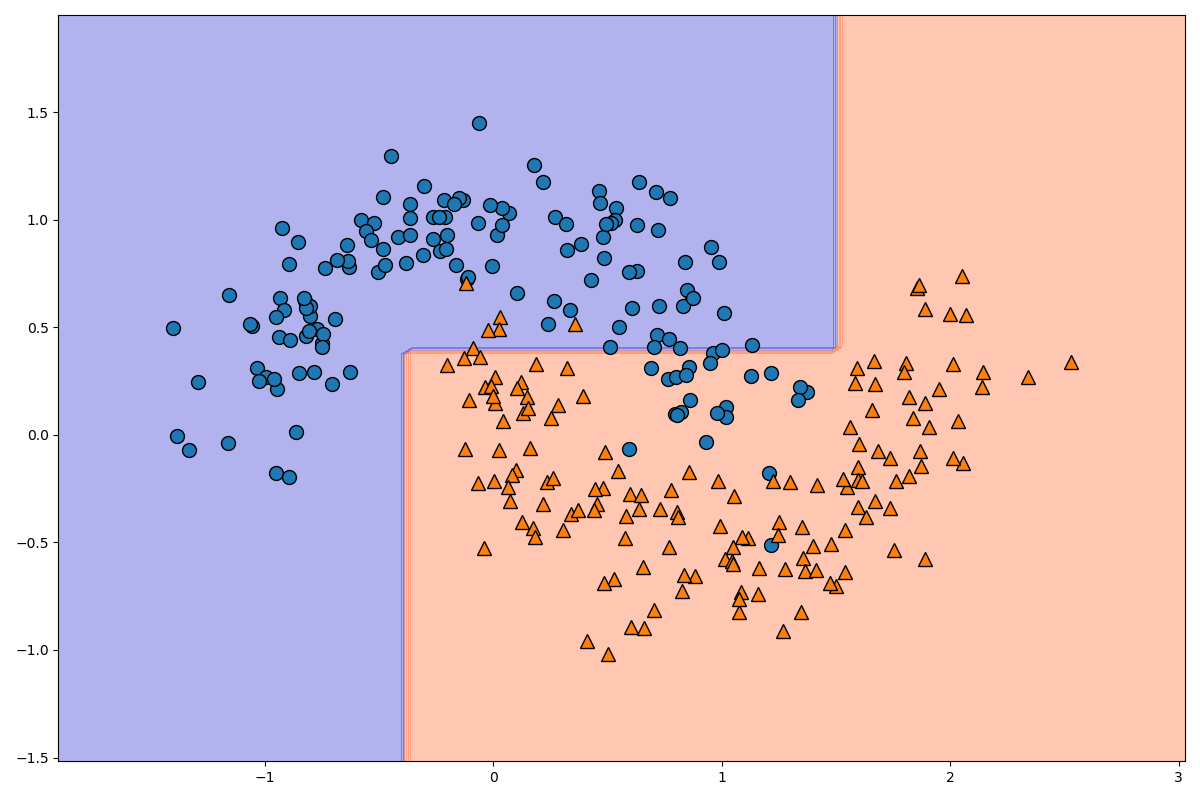
分類後のモデルを可視化してみましょう。以下のコードです。
plt.figure(figsize=(12, 8))
_x1 = np.linspace(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, 100)
_x2 = np.linspace(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, 100)
x1, x2 = np.meshgrid(_x1, _x2)
X_stack = np.hstack((x1.ravel().reshape(-1, 1), x2.ravel().reshape(-1, 1)))
y_pred = clf_model.predict(X_stack).reshape(x1.shape)
custom_cmap = ListedColormap(['mediumblue', 'orangered'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.show()
格子点を用いて色を変化させる方法についてはこちらの記事を参考にしてください。
_x1と_x2でx軸方向とy軸方向の格子点の領域を指定し、x1, x2 = np.meshgrid(_x1, _x2)で格子点を作成しています。
X_stack = np.hstack((x1.ravel().reshape(-1, 1), x2.ravel().reshape(-1, 1)))の部分で100×100の格子点を一次元配列に変化させた後、10000×1の二次元配列に変換し、水平方向に結合して10000×2のデータに変換しています。
y_pred = clf_model.predict(X_stack).reshape(x1.shape)の部分で10000×2のデータを0と1のデータに変換し、それを100×100のデータに変換しています。データを分離する線の片側が0でもう一方が1になります。
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)の部分で、等高線を描画します。色をcmap=custom_cmapで指定しています。
ここまでで分類木の実装は終了です。
回帰木の実装
それでは回帰木の実装を行いましょう。
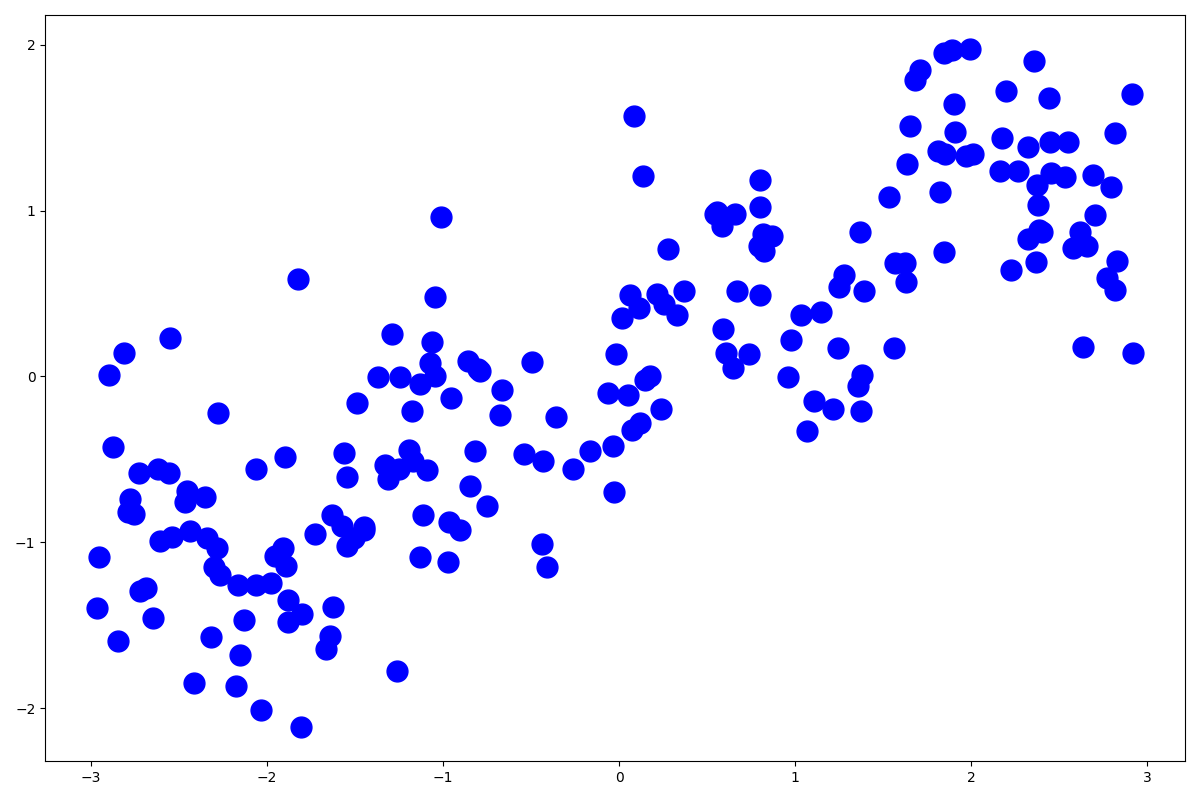
データを準備して描画してみましょう。
import mglearn
from sklearn.tree import DecisionTreeRegressor
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import export_graphviz
import graphviz
X, Y = mglearn.datasets.make_wave(n_samples=200)
plt.figure(figsize=(12, 8))
plt.plot(X, Y, 'bo', ms=15)
plt.show()
このようなデータになっています。それではモデルを作成しましょう。
tree_reg_model = DecisionTreeRegressor(max_depth=3)
tree_reg_model.fit(X, Y)
print(tree_reg_model.score(X, Y))
0.7755211625482443
scoreで$R^2$を表示させることができます。
score(self, X, y[, sample_weight]) Returns the coefficient of determination R^2 of the prediction.
あまり精度はよくありませんね。
次のコードでモデルを可視化してみましょう。
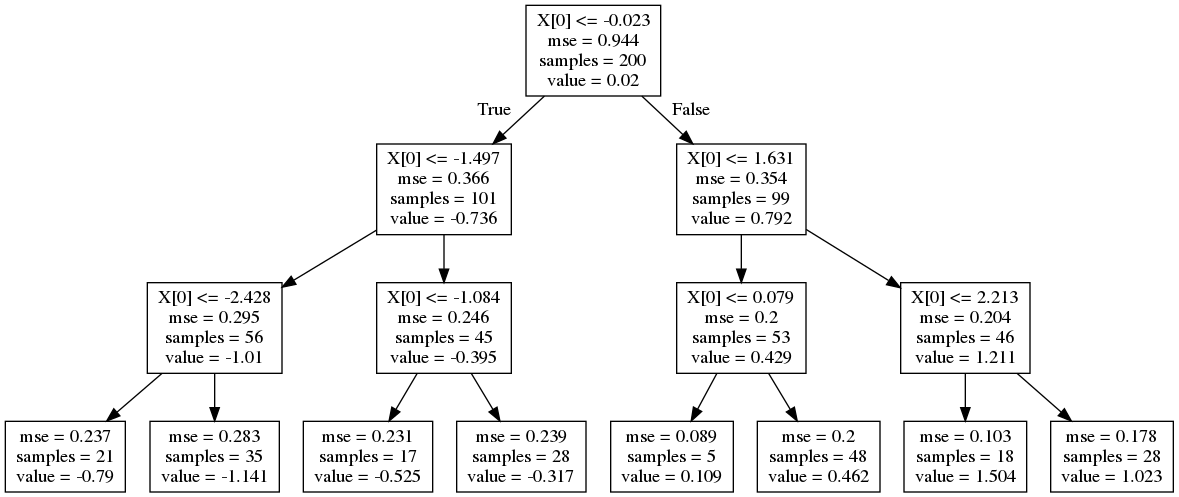
dot_data = export_graphviz(tree_reg_model)
graph = graphviz.Source(dot_data)
graph.render('wave-tree', format='png')
このように、回帰木は(決定木もそうですが)モデルの解釈性がとても良いですね。
それでは、次のコードで回帰直線を図示してみましょう。
X1 = np.linspace(X.min() - 1, X.max() + 1, 1000).reshape(-1, 1)
y_pred = tree_reg_model.predict(X1)
plt.xlabel('x', fontsize=10)
plt.ylabel('y', fontsize=10, rotation=-0)
plt.plot(X, Y, 'bo', ms=5)
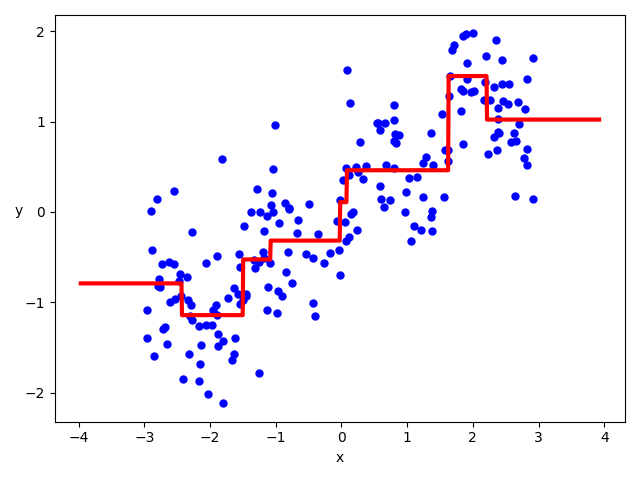
plt.plot(X1, y_pred, 'r-', linewidth=3)
plt.show()
図示してみてわかる通り、あまり正しくはありませんね。
深さを指定せずに実装
それでは、次は深さを実装せずに実装してみましょう。
深さを指定しない以外は同じなので、同じ手順は関数にまとめましょう。
import mglearn
from sklearn.tree import DecisionTreeRegressor
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import export_graphviz
import graphviz
X, Y = mglearn.datasets.make_wave(n_samples=200)
tree_reg_model_2 = DecisionTreeRegressor()
tree_reg_model_2.fit(X, Y)
print(tree_reg_model_2.score(X, Y))
1.0
$R^2$が1になりました。いったいどのようなモデルになっているのでしょうか。以下で分岐を図示しましょう。
def graph_export(model):
dot_data = export_graphviz(model)
graph = graphviz.Source(dot_data)
graph.render('test', format='png')
graph_export(tree_reg_model_2)
恐ろしいほどの分岐になりました。もう、どのように分岐しているか読めませんね。
次のコードでモデルを図示しましょう。
def plot_regression_predictions(tree_reg, x, y):
x1 = np.linspace(x.min() - 1, x.max() + 1, 500).reshape(-1, 1)
y_pred = tree_reg.predict(x1)
plt.xlabel('x', fontsize=10)
plt.ylabel('y', fontsize=10, rotation=-0)
plt.plot(x, y, 'bo', ms=5)
plt.plot(x1, y_pred, 'r-', linewidth=1)
plt.show()
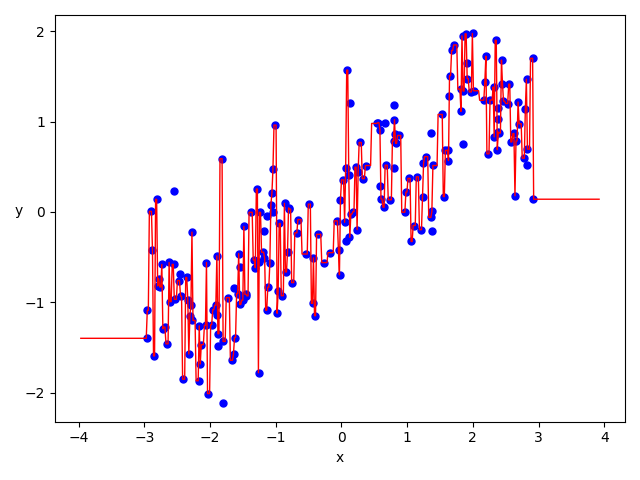
plot_regression_predictions(tree_reg_model_2, X, Y)
上の図を見て頂ければ分かりますが、これは明らかに過学習になっていますね。
これでは未知のデータを予測することができないので、適切に木の深さを設定する大切さが理解できると思います。
終わりに
今回はここまでになります。
ここまでお付き合い頂きありがとうございました。