はじめに
今回は、決定木の理論についてまとめていきます。
お付き合い頂ければ幸いです。
決定木について
決定木の概要
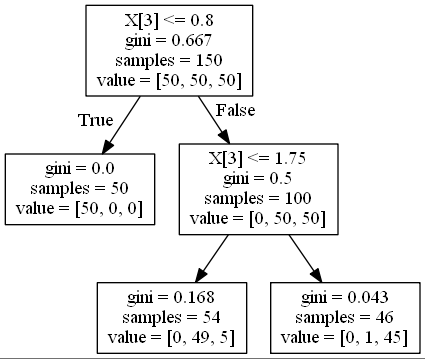
決定木の可視化すると以下のようになります。
今回はirisデータセットによる分類をscikit-learnのexport_graphvizを用いて可視化しました。
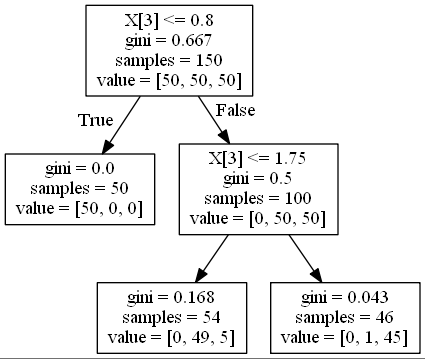
決定木とは、上の画像のようにデータをある条件に従って分割することにより、データの分類または回帰のモデルを作成するアルゴリズムです。分類を行う分類木と回帰を行う回帰木を総称して決定木と呼びます。
かなりシンプルなアルゴリズムのため、他の複雑なアルゴリズムと比較すると精度は出にくい傾向にあります。
しかし、モデルの解釈性が非常に高いです。
モデルの見た目が上の図のように木のように見えることから、決定木と呼ばれています。
代表的なアルゴリズムにCARTやC5.0などがあります。
アルゴリズムについてはこちらの記事を参考にしてください。
ここでは、ニクラス分類を繰り返し行うCARTのアルゴリズムを取り扱っていきます。
決定木の基準について
ここまでで決定木のおおよその概要をつかめたと思います。
ここでは、分類木と回帰木の枝分かれの基準について考えていきます。
分類木の基準
それでは、分類木はどのような判断基準に従って枝分かれさせていくのかを考えていきましょう。
結論から書くと、分類は不純度が最小になるような分割をする、という基準に基づいて特徴量や閾値を決めています。
不純度とはどれくらい多くのクラスが混じりあっているかを数値にしたもので、誤分類率やジニ指数、交差エントロピー誤差を用いて表されます。一つのノードに一つのクラスの観測地がある状態のとき、不純度は0になります。
回帰木の基準
回帰木は、平均二乗誤差で表されるコスト関数を定義し、そのコスト関数の重み付き和が最小となるように特徴量や閾値を選択します。
数式について
分類木
不純度を数式を用いて表してみましょう。以下の図について考えます。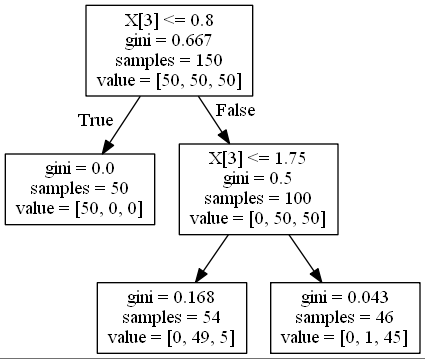
$N_m$個の観測値を持つ領域$R_m$におけるクラスkの観測値の割合を以下のように定義します。
\hat{p}_{mk} = \frac{1}{N_m} \sum_{x_i\in R_m}^{}I(y_i = k)
図の上から三番目の段に注目します。mは領域の番号を表しており、m=1でgini=0.168の領域を表し、m=2でgini=0.043の領域を表しています。kはクラスラベルを表していて、今回はvalueの部分の左からクラス1、クラス2、クラス3と定義しています。
数式にすると難しそうですが、実際に計算すると以下のようになります。
\hat{p}_{11} = \frac{0}{54} \quad \hat{p}_{12} = \frac{49}{54} \quad \hat{p}_{13} = \frac{5}{54}
なんとなく数式の意味が理解できたでしょうか。
この$\hat{p}$を用いて、以下の三つの関数で不純度を表現します。
誤分類率
\frac{1}{N_m} \sum_{x_i\in R_m}^{}I(y_i \neq k(m)) = 1-\hat{p}_{mk}
ジニ指数
1 - \sum_{k=1}^{K}\hat{p}_{mk}
交差エントロピー誤差
-\sum_{k=1}^{K}\hat{p}_{mk}log\hat{p}_{mk}
sklearnで標準で用いる不純度の関数はジニ指数になっているので、実際にジニ指数を計算してみましょう。
三段目の不純度をジニ指数を用いて計算します。
左のgini=0.168のノードのジニ指数は以下の式になりますね。
1 - (\frac{0}{54})^2 - (\frac{49}{54})^2 - (\frac{5}{54})^2 = 0.168
当然答えは0.168になります。上の式がsklearnが内部で行っている計算式になります。ついでに右のgini=0.043のノードの計算も行いましょう。
1 - (\frac{0}{46})^2 - (\frac{1}{46})^2 - (\frac{45}{46})^2 = 0.043
こちらも一致しましたね。それでは、それぞれのにデータの重みをかけることで全体の不純度を計算しましょう。以下の式になります。
\frac{54}{100} ×0.168 + \frac{46}{100} ×0.043 = 0.111
これで全体の不純度が導出できました。決定木はこの不純度を小さくするような特徴量や閾値を選択することにより、モデルを構築しています。
回帰木
回帰木において、コスト関数を以下のように定義します。
\hat{c}_m = \frac{1}{N_m}\sum_{x_i \in R_m}^{}y_i\\
Q_m(T) = \frac{1}{N_m} \sum_{x_i \in R_m}(y_i - \hat{c}_m)^2
$\hat{c}_m$がそのノードに含まれる観測値の平均を表しているので、コスト関数は平均二乗誤差となります。
このコスト関数はそれぞれのノードについて計算されるため、そのコスト関数の重み付き和が最小となるように特徴量や閾値を設定します。
終わりに
今回の記事はここまでになります。
お付き合い頂きありがとうございました。
よろしければ次回の記事もご覧ください。