【Unity】C# Job System + Burstで波動方程式を実装し、 ShaderGraphで水を描画する

はじめに

波を作ってみたので紹介します。
YouTube

C# Job Systemで波動方程式を実装し、ShaderGraphで水を描画しています。

GitHub
https://github.com/rngtm/Unity-JobSystem-WaveEquation

§1 . 波動方程式

2次元の波の運動は以下の数式で表されます。

\frac{\partial^2 u }{\partial t^2} = s^2 \left( \frac{\partial^2 u }{\partial x^2} + \frac{\partial^2 u }{\partial y^2} \right)

$u = u(x,y,t)$ は水面の波の変位、$s$は波の伝わる速さを表しています。

§2 . 関数f(x, y)の2階微分の計算

ここで、関数xとyの関数 $f(x,y)$　の2階微分は、ある小さな値 $h$ を使って以下の式で計算することができます。

$$
\frac{\partial^2}{\partial x^2}f(x, y) = \frac{f(x + h, y) + f(x - h,y) - 2 f(x,y)}{h^2} + O(h^2)
$$

$$
\frac{\partial^2}{\partial y^2}f(x, y) = \frac{f(x, y + h) + f(x,y - h) - 2 f(x,y)}{h^2} + O(h^2)
$$

$O(h^2)$は誤差を表しており、$h$を$0$に近づけるほど、誤差$O(h^2)$は0に近づきます。

※上記の式はテイラー展開を利用することで導出できますが、ここでは説明しません。
参考 : https://na.cs.tsukuba.ac.jp/jikken/wp-content/uploads/2016/07/wave.pdf

§3 . 波の加速度の計算

ここでは、時刻tにおける波の変位を $u(x,y)$ と表します。

先ほどの §2. の計算式の $ f(x,y) \rightarrow u(x,y)$ と置き換えると、$u$の$x, y$に関する2階微分を得ることができます。
$h$は$\Delta x, \Delta y$に置き換えます。

$$
\frac{\partial^2}{\partial x^2}u(x, y) \approx \frac{u(x + \Delta x, y) + f(x - \Delta x,y) - 2 u(x,y)}{(\Delta x)^2}
$$

$$
\frac{\partial^2}{\partial y^2}u(x, y) \approx \frac{u(x, y + \Delta y) + f(x,y - \Delta y) - 2 u(x,y)}{(\Delta y)^2}
$$

2階微分の足し合わせに波の伝わる速さ $s^2$を乗算すると、波の加速度 $ \frac{\partial^2 u }{\partial t^2} $　が求まります。

$$
\frac{\partial^2 u }{\partial t^2} = s^2 \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u }{\partial y^2} \right)
$$

§4. MonoBehaviourで波動方程式を実装してみる

まずはC# Job Systemを使わず、通常のMonoBehaviourで波動方程式シミュレーションを実装してみました。

ソースコード全体(WaveMesh2D.cs)

WaveMesh2D.cs

using System.Linq;
using UnityEngine;

/// <summary>
/// 2次元の波動方程式の実装
/// </summary>
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class WaveMesh2D : MonoBehaviour
{
    [SerializeField] private Vector2Int resolution = new Vector2Int(16, 16); // メッシュ解像度
    [SerializeField] private float s = 0.5f; // 波の伝わる速さ
    [SerializeField] private Vector2 meshSize = new Vector2(8f, 8f);
    private Mesh mesh;
    private Vector3[] vertices = null;
    private Vector3[] normals = null;
    private float[,] waveTable; // 波の変位
    private float[,] waveSpeedTable;

    [SerializeField] private float rainForceMin = 0.1f;
    [SerializeField] private float rainForceMax = 0.3f;
    [SerializeField] private int rainIntervalFrame = 10;

    // Start is called before the first frame update
    void Start()
    {
        // 波のデータ作成
        waveTable = new float[resolution.x, resolution.y];
        waveSpeedTable = new float[resolution.x, resolution.y];

        // 波の初期化
        InitializeWave();
        
        // メッシュの作成
        CreateMesh();
    }

    /// <summary>
    /// 波の初期状態の設定
    /// </summary>
    private void InitializeWave()
    {
        // 座標(1,1)を中心にして、水を持ち上げます
        Vector2 center = new Vector2(1f, 1f);
        for (int yi = 1; yi < resolution.y - 1; yi++) // 端点(yi = 0, yi = resolution.y - 1 ) は固定する
        {
            for (int xi = 1; xi < resolution.x - 1; xi++) // 端点(xi = 0, xi = resolution.x - 1 ) は固定する
            {
                var p = GetVertexPosition(xi, yi);
                float r = (new Vector2(p.x, p.z) - center).magnitude;
                float h = Mathf.Exp(-r * 8.0f) * 2.0f;
                h = Mathf.Clamp01(h);
                waveTable[xi, yi] = h;
            }
        }
    }

    void FixedUpdate()
    {
        SolveWaveEquation(Time.fixedDeltaTime);
    }

    // 2次元波動方程式の実装
    void SolveWaveEquation(float deltaTime)
    {
        float dx = meshSize.x / resolution.x;
        float dy = meshSize.y / resolution.y;

        // 位置を元に加速度 (d/dt)^2 u の計算
        for (int yi = 1; yi < resolution.y - 1; yi++)
        {
            for (int xi = 1; xi < resolution.x - 1; xi++)
            {
                float wave = waveTable[xi, yi];
                float waveX1 = waveTable[xi - 1, yi];
                float waveX2 = waveTable[xi + 1, yi];
                float waveY1 = waveTable[xi, yi - 1];
                float waveY2 = waveTable[xi, yi + 1];
                
                // (d/dx)^2 u     
                float dudx2 = (waveX1 + waveX2 - 2f * wave) / dx / dx;
                
                // (d/dy)^2 u     
                float dudz2 = (waveY1 + waveY2 - 2f * waveTable[xi, yi]) / dy / dy;

                float waveAccel = s * s * (dudx2 + dudz2);
                waveSpeedTable[xi, yi] += waveAccel * deltaTime;
            }
        }
        
        // 速度の反映
        for (int yi = 1; yi < resolution.y - 1; yi++)
        {
            for (int xi = 1; xi < resolution.x - 1; xi++)
            {
                waveTable[xi, yi] += waveSpeedTable[xi, yi] * deltaTime;
            }
        }

        UpdateMesh();
    }

    /// <summary>
    /// メッシュ作成
    /// </summary>
    void CreateMesh()
    {
        mesh = new Mesh();

        // 頂点の作成
        int vertexCount = resolution.x * resolution.y;

        // 頂点・法線・UV作成
        vertices = new Vector3[vertexCount];
        normals = new Vector3[vertexCount].Select(x => new Vector3(0, 1, 0)).ToArray();
        
        var uv = new Vector2[vertexCount];
        int vi = 0;
        for (int yi = 0; yi < resolution.y; yi++)
        {
            for (int xi = 0; xi < resolution.x; xi++)
            {
                vertices[vi] = GetVertexPosition(xi, yi);
                uv[vi] = new Vector2((float)xi / (resolution.x - 1), (float)yi / (resolution.y - 1));
                vi++;
            }
        }

        // 頂点インデックス作成
        int triangleCount = (resolution.x - 1) * (resolution.y - 1) * 6;
        int[] triangles = new int[triangleCount];
        int offset = 0;
        int ti = 0;
        for (int yi = 0; yi < resolution.y - 1; yi++)
        {
            for (int xi = 0; xi < resolution.x - 1; xi++)
            {
                triangles[ti++] = offset;
                triangles[ti++] = offset + resolution.x;
                triangles[ti++] = offset + 1;
                triangles[ti++] = offset + resolution.x;
                triangles[ti++] = offset + resolution.x + 1;
                triangles[ti++] = offset + 1;

                offset += 1;
            }

            offset += 1;
        }

        mesh.SetVertices(vertices);
        mesh.uv = uv;
        mesh.SetTriangles(triangles, 0);

        GetComponent<MeshFilter>().mesh = mesh;
    }

    /// <summary>
    /// メッシュ更新
    /// </summary>
    private void UpdateMesh()
    {
        float dx = meshSize.x / resolution.x;
        float dy = meshSize.y / resolution.y;
        int vi = 0;
        for (int yi = 0; yi < resolution.y; yi++)
        {
            for (int xi = 0; xi < resolution.x; xi++)
            {
                vertices[vi] = GetVertexPosition(xi, yi);
                vi++;
            }
        }

        for (int yi = 0; yi < resolution.y - 1; yi++)
        {
            for (int xi = 0; xi < resolution.x - 1; xi++)
            {
                // 法線の計算
                float dudx = (waveTable[xi + 1, yi] - waveTable[xi - 1, yi]) / dx;
                float dudy = (waveTable[xi, yi] - waveTable[xi - 1, yi]) / dy;
                normals[xi + yi * resolution.x] = new Vector3(-dudx, 1.0f, -dudy).normalized;
            }
        }

        mesh.SetVertices(vertices);
        mesh.SetNormals(normals);
    }

    /// <summary>
    /// 現在の頂点座標の取得
    /// </summary>
    private Vector3 GetVertexPosition(int x, int y)
    {
        return new Vector3(
            (float) x / resolution.x * meshSize.x - meshSize.x / 2f,
            waveTable[x, y],
            (float) y / resolution.y * meshSize.y - meshSize.y / 2f
        );
    }
}

波動方程式の計算部分(抜粋)

    // 2次元波動方程式の計算 (FixedUpdate()から呼ぶ想定)
    void SolveWaveEquation(float deltaTime)
    {
        float dx = meshSize.x / resolution.x;
        float dy = meshSize.y / resolution.y;

        // 波の速度の計算
        for (int yi = 1; yi < resolution.y - 1; yi++)
        {
            for (int xi = 1; xi < resolution.x - 1; xi++)
            {
                float wave = waveTable[xi, yi]; // u(x, y)
                float waveX1 = waveTable[xi - 1, yi]; // u(x - dx, y)
                float waveX2 = waveTable[xi + 1, yi]; // u(x + dx, y)
                float waveY1 = waveTable[xi, yi - 1]; // u(x, y - dy)
                float waveY2 = waveTable[xi, yi + 1]; // u(x, y + dy)
                
                // (d/dx)^2 u     
                float dudx2 = (waveX1 + waveX2 - 2f * wave) / dx / dx;
                
                // (d/dy)^2 u     
                float dudz2 = (waveY1 + waveY2 - 2f * wave) / dy / dy;

                // 加速度(d/dt)^2 u の計算
                float waveAccel = s * s * (dudx2 + dudz2);
                
                // 加速度を使って速度を更新
                waveSpeedTable[xi, yi] += waveAccel * deltaTime;
            }
        }
        
        // 速度を使って位置を更新
        for (int yi = 1; yi < resolution.y - 1; yi++)
        {
            for (int xi = 1; xi < resolution.x - 1; xi++)
            {
                waveTable[xi, yi] += waveSpeedTable[xi, yi] * deltaTime;
            }
        }

        UpdateMesh();
    }

補足 : メッシュの法線の計算方法

水面メッシュの点$P(x,y,u(x,y))$ における長さ1の法線ベクトル $ \vec{n}$の計算方法を軽く紹介します。
法線ベクトルの計算は、C#では以下のような実装になっています。

// 法線の計算
float dudx = (waveTable[xi + 1, yi] - waveTable[xi - 1, yi]) / dx;
float dudy = (waveTable[xi, yi] - waveTable[xi - 1, yi]) / dy;
normals[xi + yi * resolution.x] = new Vector3(-dudx, 1.0f, -dudy).normalized;

\vec{n} = 
\begin{vmatrix}
- \Delta u_x / \Delta x \\
- \Delta u_y / \Delta y \\
1
\end{vmatrix}
\\\\
\Delta u_x = u(x + \Delta x, y) - u(x, y)
\\\\
\Delta u_y = u(x, y + \Delta y) - u(x, y)

法線ベクトルの導出(ちょっと長いです)

■法線ベクトルの導出

水面にある点$P$からx方向に少しずれた位置にある水面上の点 $Q$と、
y方向に少しずれた位置にある水面上の点 $R$ を考えます。
$\vec{PQ}$ と $\vec{PR}$ の外積を計算することで、点Pの法線方向のベクトルを得ることができます。

■法線の計算

点P, Q, R は以下のようなベクトル形式で表すことができます。

P = \begin{pmatrix}
x \\
y \\
u(x,y)
\end{pmatrix}

Q = \begin{pmatrix}
x + \Delta x \\
y \\
u(x+\Delta x,y)
\end{pmatrix}

R = \begin{pmatrix}
x \\
y + \Delta y \\
u(x,y + \Delta y)
\end{pmatrix}

$\vec{PQ}$ と $\vec{PR}$ は以下のようなベクトルになります。

\vec{PQ} = \begin{pmatrix}
\Delta x \\
0 \\
u(x+\Delta x,y) - u(x,y) 
\end{pmatrix}
= \begin{pmatrix}
\Delta x \\
0 \\
\Delta u_x
\end{pmatrix}

\vec{PR} =  \begin{pmatrix}
0 \\
dy \\
u(x,y+\Delta y) - u(x,y) 
\end{pmatrix}
= \begin{pmatrix}
0 \\
dy \\
\Delta u_y
\end{pmatrix}

$\vec{PQ}$ と $\vec{PR}$ の外積を計算すると、以下のようになります。

\vec{PQ} \times \vec{PR}  
= 
\begin{pmatrix}
\Delta x\\
0 \\
\Delta u_y
\end{pmatrix}
\times
\begin{pmatrix}
0 \\
\Delta y \\
\Delta u_y
\end{pmatrix}
=
\begin{pmatrix}
- \Delta y \Delta u_x \\
- \Delta x \Delta u_y \\
\Delta x \Delta y
\end{pmatrix}
=
\begin{pmatrix}
- \Delta u_x / \Delta x \\
- \Delta u_y / \Delta y \\
1
\end{pmatrix}
\Delta x \Delta y

$ \vec{PQ} \times \vec{PR} $ を正規化すると、係数の $ \Delta x \Delta y $ は消え、長さ1の法線ベクトル $\vec{n}$ を得ます。

| \vec{PQ} \times \vec{PR} |
= \begin{vmatrix}
- \Delta u_x / \Delta x \\
- \Delta u_y / \Delta y \\
1
\end{vmatrix}
= \vec{n}

z方向下向きの法線ベクトルが欲しいときは、-1倍します。

\begin{vmatrix}
\Delta u_x / \Delta x \\
\Delta u_y / \Delta y \\
-1
\end{vmatrix}

(法線ベクトルの導出おわり)

---

$5. C# Job Systemで波動方程式を実装する

§4. の 波動シミュレーションをJobSystemに移植します。

移植に当たって以下のようなcsファイルを用意しました。

csファイル名	説明
WaveParameter.cs	波のパラメータを保持する構造体
WaveSpeedJob.cs	波動方程式を計算し、波の速度を更新するジョブ
WavePositionJob.cs	波の速度を利用して、波の位置を更新するジョブ。 WaveSpeedJobの後に実行
WaveMesh2D_Job.cs	波の状態をMeshへ反映するMonoBehaviourクラス
WaveJobSystem.cs	JobSystemを実行する大元のMonoBehaviourクラス

Unity上での実装を見たい方は、GitHubリポジトリをご覧ください
https://github.com/rngtm/Unity-JobSystem-WaveEquation

ソースコード

WaveParameter.cs (波のパラメータの構造体)

WaveParameter.cs

using System;
using UnityEngine;

/// <summary>
/// 波のパラメータ
/// </summary>
[Serializable]
public struct WaveParameter
{
    public int NumX; // グリッドの数(X)
    public int NumY; // グリッドの数(Y)
    public float DeltaX; // グリッド間の距離(X方向)
    public float DeltaY; // グリッド間の距離(Y方向)
    public float V; // 波が伝わる速さ
    public Vector2 MeshSize; // メッシュの大きさ
}

WaveSpeedJob.cs (波の速さを更新するジョブ)

WaveSpeedJob.cs

using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;

/// <summary>
/// 波の加速度・速度を計算するJob
/// </summary>
[BurstCompile]
public struct WaveSpeedJob : IJobParallelFor
{
    [ReadOnly] public WaveParameter Parameter;
    [ReadOnly] public NativeArray<float> WaveArray; // 波の変位u
    public NativeArray<float> Accel; // 波の加速度　(d/dt)^2 u
    public NativeArray<float> Speed; // 波の速さ (d/dt) u
    public float DeltaTime;

    public void Execute(int index)
    {
        int xi = index % Parameter.NumX;
        int yi = index / Parameter.NumX;
        
        // 端点の場合は何もしない
        if (xi == 0 || xi == Parameter.NumX - 1) return;
        if (yi == 0 || yi == Parameter.NumY - 1) return;

        float wave = GetWave(xi, yi);
        float waveX1 = GetWave(xi - 1, yi);
        float waveX2 = GetWave(xi + 1, yi);
        float waveY1 = GetWave(xi, yi - 1);
        float waveY2 = GetWave(xi, yi + 1);
        
        float d2ux = (waveX1 + waveX2 - 2f * wave) / (2f);
        float d2uy = (waveY1 + waveY2 - 2f * wave) / (2f);

        float dvdx = (Parameter.V / Parameter.DeltaX);
        Accel[index] = dvdx * dvdx * (d2ux + d2uy) * DeltaTime;
        Speed[index] += Accel[index] * DeltaTime;
    }

    float GetWave(int xi, int yi)
    {
        return WaveArray[xi + yi * Parameter.NumX];
    }
}

WavePositionJob.cs (波の位置(変位u)を更新するジョブ)

WavePositionJob.cs

using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;

/// <summary>
/// 波のSpeedを元にして、波の変位uを更新するJob
/// </summary>
[BurstCompile]
public struct WavePositionJob : IJobParallelFor
{
    [ReadOnly] public float DeltaTime;
    [ReadOnly] public NativeArray<float> Speed; // 波の速さ (d/dt) u
    public NativeArray<float> Position; // 波の速さ (d/dt) u

    public void Execute(int index)
    {
        // 波の変位の更新
        Position[index] += Speed[index] * DeltaTime;
    }
}

WaveMesh2D_Job.cs (波のメッシュを管理するMonoBehaviourクラス)

WaveMesh2D_Job.cs

using System.Linq;
using Unity.Collections;
using UnityEngine;

/// <summary>
/// 波のメッシュを管理するクラス(C# JobSystemから動かす)
/// </summary>
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class WaveMesh2D_Job : MonoBehaviour
{
    private WaveParameter parameter;
    private NativeArray<float> waveTable;
    private Vector2Int resolution; // メッシュ解像度
    private Mesh mesh = null;
    private Vector3[] vertices = null;
    private Vector3[] normals = null;
    
    /// <summary>
    /// 波の初期化
    /// </summary>
    public void Create(WaveParameter parameter, NativeArray<float> waveArray)
    {
        this.parameter = parameter;
        resolution = new Vector2Int(parameter.NumX, parameter.NumY);
        waveTable = waveArray;
        CreateMesh();
    }

    /// <summary>
    /// メッシュ作成
    /// </summary>
    void CreateMesh()
    {
        mesh = new Mesh();

        // 頂点の作成
        int vertexCount = resolution.x * resolution.y;

        // 頂点・法線・UV作成
        vertices = new Vector3[vertexCount];
        normals = new Vector3[vertexCount].Select(x => new Vector3(0, 1, 0)).ToArray();
        
        var uv = new Vector2[vertexCount];
        int vi = 0;
        for (int yi = 0; yi < resolution.y; yi++)
        {
            for (int xi = 0; xi < resolution.x; xi++)
            {
                vertices[vi] = GetVertexPosition(xi, yi);
                uv[vi] = new Vector2((float)xi / (resolution.x - 1), (float)yi / (resolution.y - 1));
                vi++;
            }
        }

        // 頂点インデックス作成
        int triangleCount = (resolution.x - 1) * (resolution.y - 1) * 6;
        int[] triangles = new int[triangleCount];
        int offset = 0;
        int ti = 0;
        for (int yi = 0; yi < resolution.y - 1; yi++)
        {
            for (int xi = 0; xi < resolution.x - 1; xi++)
            {
                triangles[ti++] = offset;
                triangles[ti++] = offset + resolution.x;
                triangles[ti++] = offset + 1;
                triangles[ti++] = offset + resolution.x;
                triangles[ti++] = offset + resolution.x + 1;
                triangles[ti++] = offset + 1;

                offset += 1;
            }

            offset += 1;
        }

        mesh.SetVertices(vertices);
        mesh.uv = uv;
        mesh.SetTriangles(triangles, 0);

        GetComponent<MeshFilter>().mesh = mesh;
    }

    /// <summary>
    /// メッシュ更新
    /// </summary>
    public void UpdateMesh()
    {
        float dx = parameter.MeshSize.x / resolution.x;
        float dy = parameter.MeshSize.y / resolution.y;
        int vi = 0;
        for (int yi = 0; yi < resolution.y; yi++)
        {
            for (int xi = 0; xi < resolution.x; xi++)
            {
                vertices[vi] = GetVertexPosition(xi, yi);
                vi++;
            }
        }

        for (int yi = 1; yi < resolution.y - 1; yi++)
        {
            for (int xi = 1; xi < resolution.x - 1; xi++)
            {
                // 法線の計算
                float dudx = (GetWave(xi + 1, yi) - GetWave(xi - 1, yi)) / parameter.DeltaX;
                float dudy = (GetWave(xi, yi) - GetWave(xi - 1, yi)) / parameter.DeltaY;
                normals[xi + yi * resolution.x] = new Vector3(-dudx, 1.0f, -dudy).normalized;
            }
        }

        mesh.SetVertices(vertices);
        mesh.SetNormals(normals);
    }

    private Vector3 GetVertexPosition(int x, int y)
    {
        return new Vector3(
            (float) x / resolution.x * parameter.MeshSize.x - parameter.MeshSize.x / 2f,
            GetWave(x, y),
            (float) y / resolution.y * parameter.MeshSize.y - parameter.MeshSize.y / 2f
        );
    }

    private float GetWave(int x, int y)
    {
        return waveTable[x + y * resolution.x];
    }
}

WaveJobSystem.cs (JobSystemを実行するMonoBehaviourクラス)

WaveJobSystem.cs

using Unity.Collections;
using Unity.Jobs;
using UnityEngine;

public class WaveJobSystem : MonoBehaviour
{
    [SerializeField] private WaveMesh2D_Job waveMesh = null;
    [SerializeField] private WaveParameter parameter = new WaveParameter();
    private NativeArray<float> accelArray;
    private NativeArray<float> speedArray;
    private NativeArray<float> waveArray;

    void Start()
    {
        // Native Arrayのメモリ割り当て
        int arrayLength = parameter.NumX * parameter.NumY;
        accelArray = new NativeArray<float>(arrayLength, Allocator.Persistent);
        speedArray = new NativeArray<float>(arrayLength, Allocator.Persistent);
        waveArray = new NativeArray<float>(arrayLength, Allocator.Persistent);
        
        // 波の初期状態の設定
        InitializeWave();
        
        // Mesh作成
        waveMesh.Create(parameter, waveArray);
    }
    
    private void FixedUpdate()
    {
        RunJob();
        waveMesh.UpdateMesh();
    }

    /// <summary>
    /// ジョブの実行
    /// </summary>
    private void RunJob()
    {
        float deltaTime = Time.fixedDeltaTime;
        var speedJob = new WaveSpeedJob
        {
            Accel = accelArray,
            Speed = speedArray,
            WaveArray = waveArray,
            Parameter = parameter,
            DeltaTime = deltaTime,
        };

        var speedHandle = speedJob.Schedule(speedArray.Length, 1);

        var positionJob = new WavePositionJob
        {
            Speed = speedArray,
            Position = waveArray,
            DeltaTime = deltaTime,
        };

        var positionHandle = positionJob.Schedule(speedArray.Length, 1, speedHandle);
        positionHandle.Complete();
    }

    /// <summary>
    /// 波の初期化
    /// </summary>
    private void InitializeWave()
    {
        Vector2 center = new Vector2(1f, 1f);
        int i = 0;
        for (int yi = 0; yi < parameter.NumY; yi++)
        {
            for (int xi = 0; xi < parameter.NumX; xi++)
            {
                var p = GetVertexPosition(xi, yi);
                float r = (new Vector2(p.x, p.z) - center).magnitude;
                float h = Mathf.Exp(-r * 8.0f) * 2.0f;
                h = Mathf.Clamp01(h);
                waveArray[i++] = h;
            }
        }
    }
    
    /// <summary>
    /// 頂点座標取得
    /// </summary>
    /// <param name="x"></param>
    /// <param name="y"></param>
    /// <returns></returns>
    private Vector3 GetVertexPosition(int x, int y)
    {
        return new Vector3(
            (float) x / parameter.NumX * parameter.MeshSize.x - parameter.MeshSize.x / 2f,
            GetWave(x, y),
            (float) y / parameter.NumY * parameter.MeshSize.y - parameter.MeshSize.y / 2f
        );
    }

    /// <summary>
    /// 波の取得
    /// </summary>
    /// <param name="x"></param>
    /// <param name="y"></param>
    /// <returns></returns>
    private float GetWave(int x, int y)
    {
        return waveArray[x + y * parameter.NumX];
    }
    
    /// <summary>
    /// NativeArrayの解放 (確保したNativeArrayは自分で開放する必要がある)
    /// </summary>
    private void OnDestroy()
    {
        waveArray.Dispose();
        speedArray.Dispose();
        accelArray.Dispose();
    }
}

JobSystemのBurst対応について

BurstCompileアトリビュートをJobの頭につけることで、Burst対応されます。

WavePositionJob.cs

[BurstCompile]
public struct WavePositionJob : IJobParallelFor
{
...

$6. ShaderGraphで水を描画する

水の描画方法は複数考えられます。
・地面のレンダリング結果に水面を上から重ねる
・地面レンダリングのUVを水面の法線でゆがませる
・光を水面で屈折させて地面を描画する
など

今回はRayを水面で屈折させて地面を描画することにしてみました。

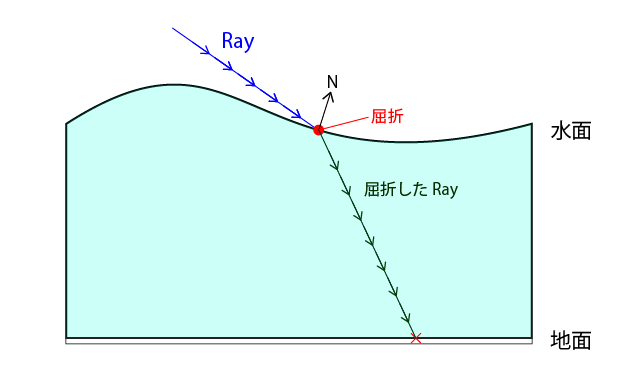
Rayの屈折

Rayを水面で屈折させて、地面を描画します。

具体的な手順

1. Cameraから、水面メッシュへ向けてRayを飛ばす
2. メッシュ上の法線を利用して、Rayの向きを屈折させる
3. 屈折したRayが地面にぶつかった位置の座標をテクスチャ座標として利用して、地面テクスチャを描画する

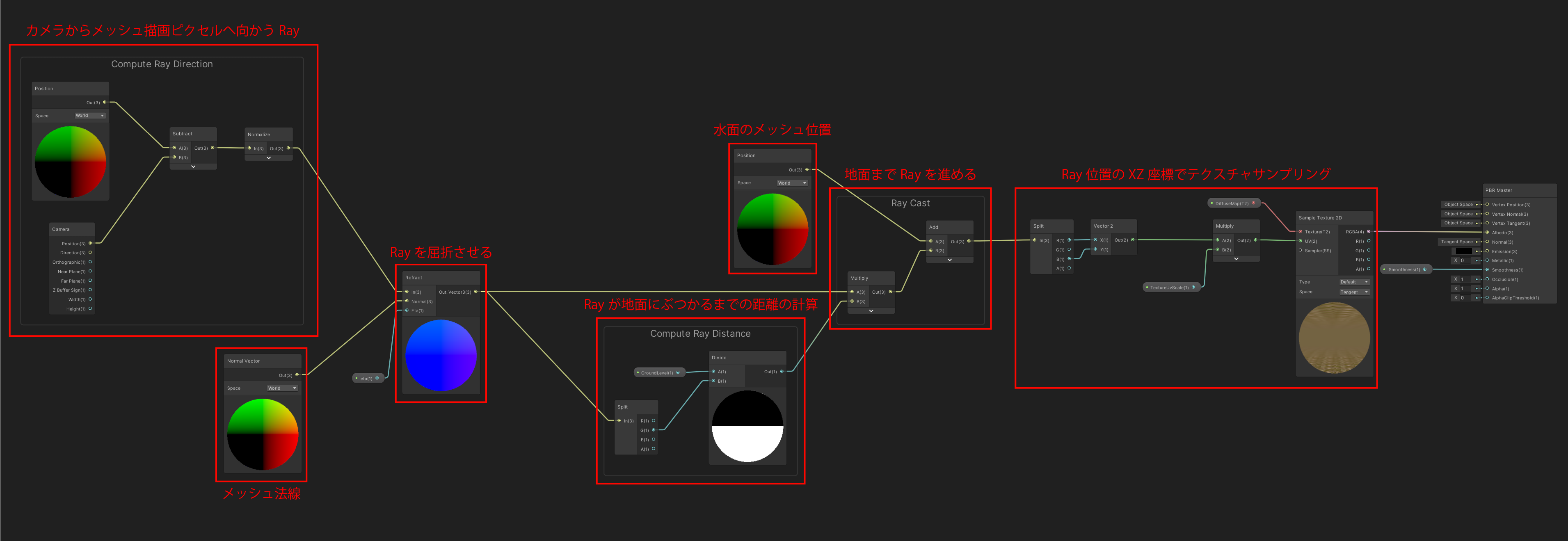
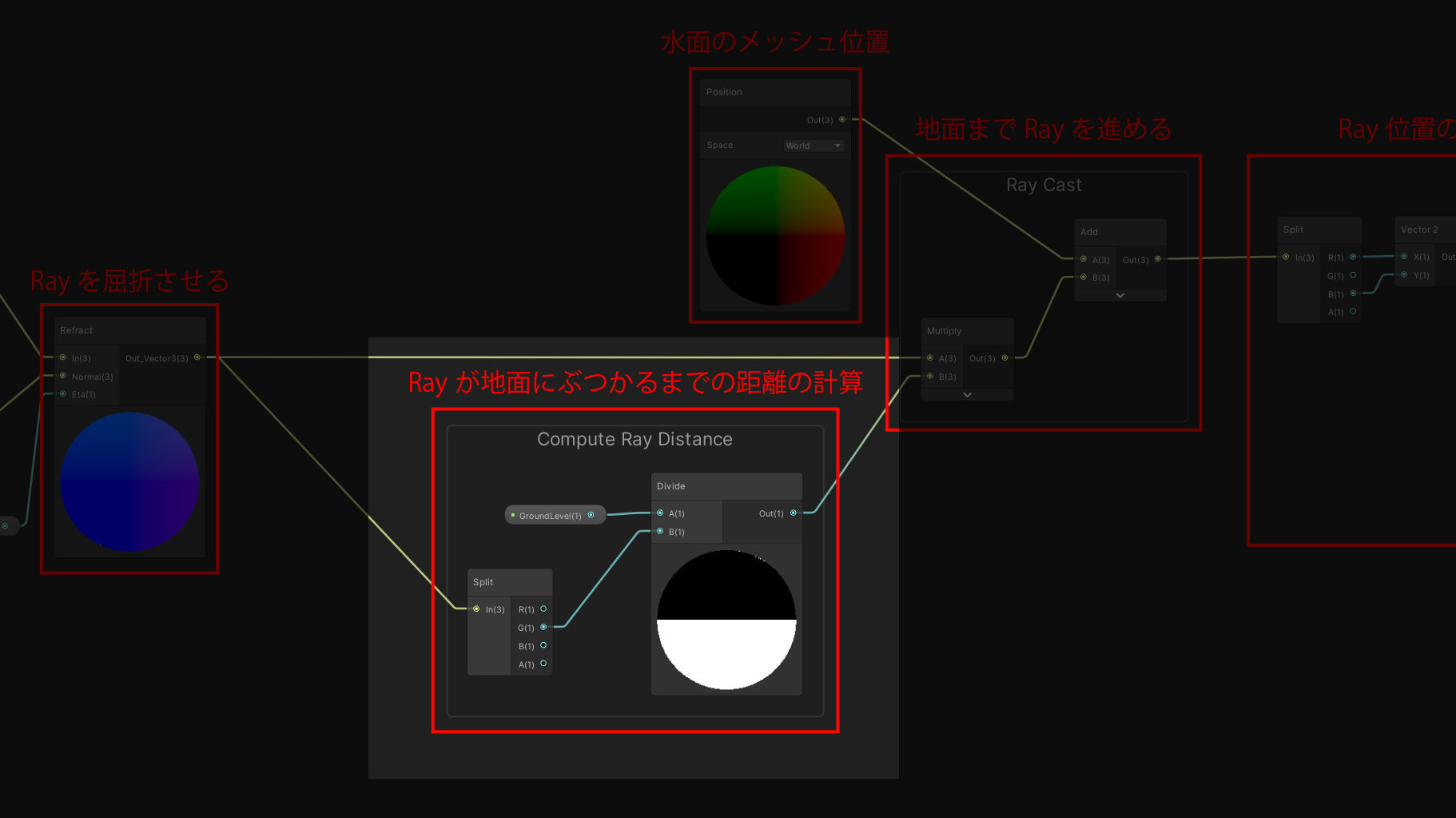
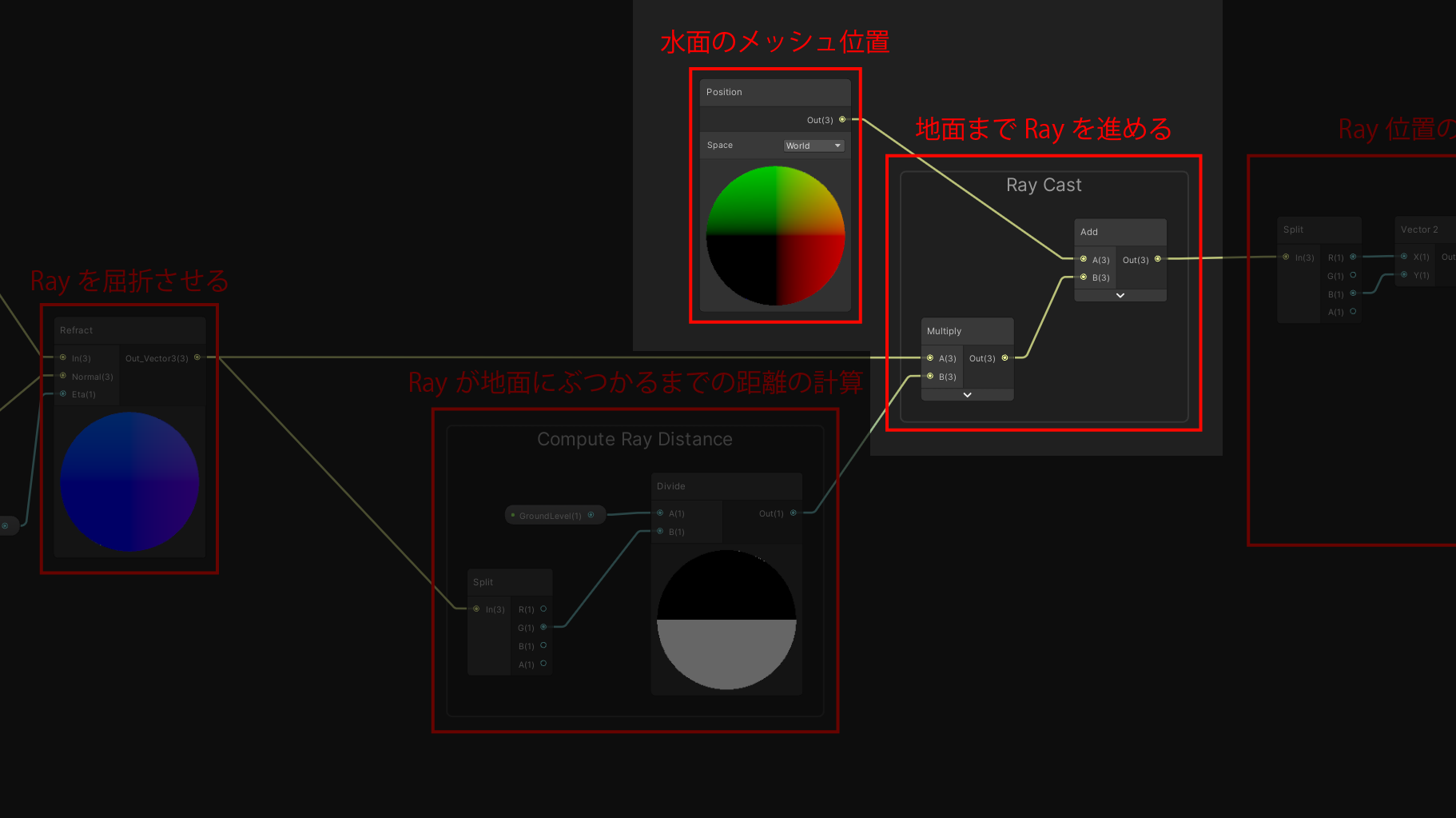
ShaderGraphの実装

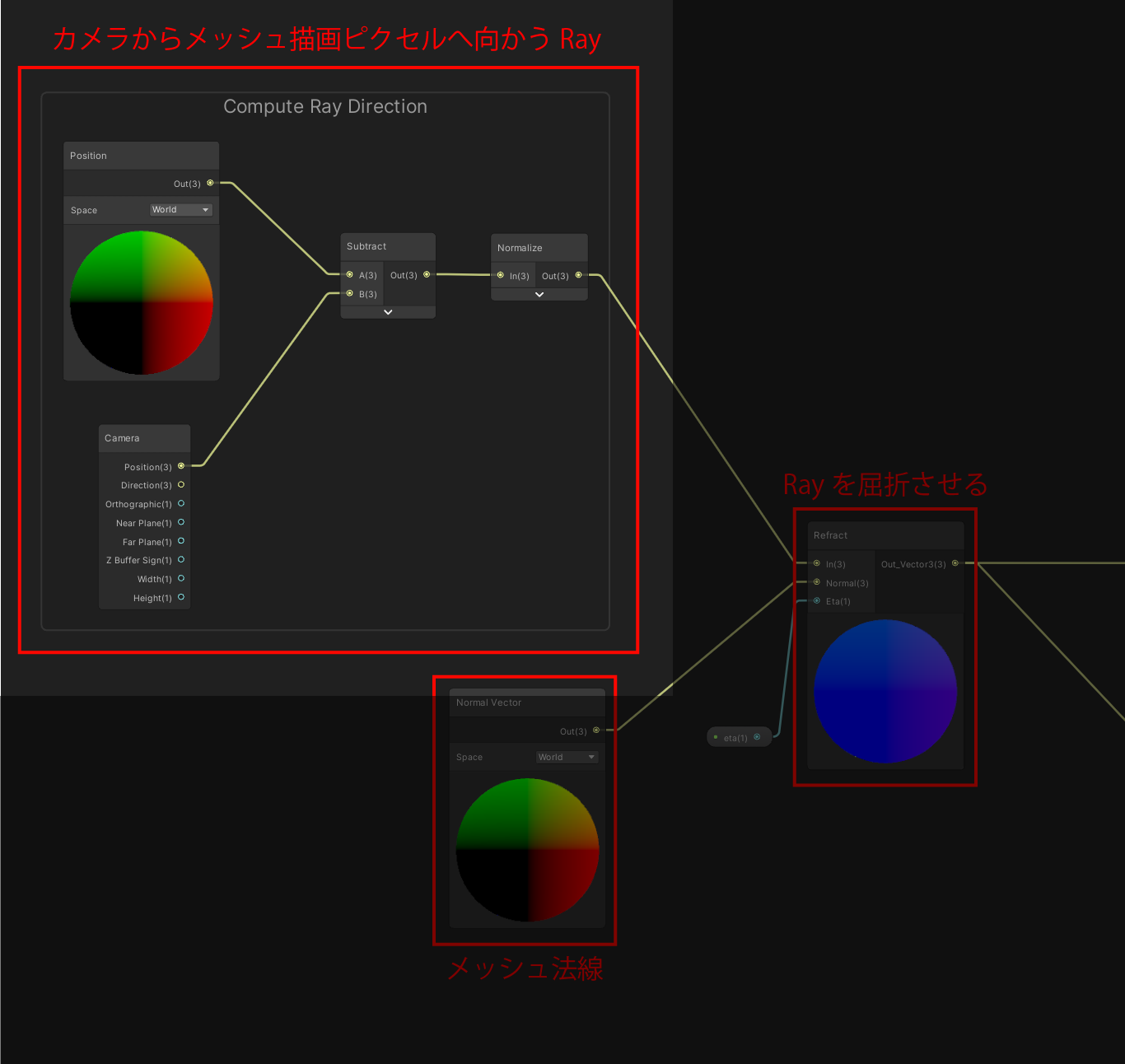
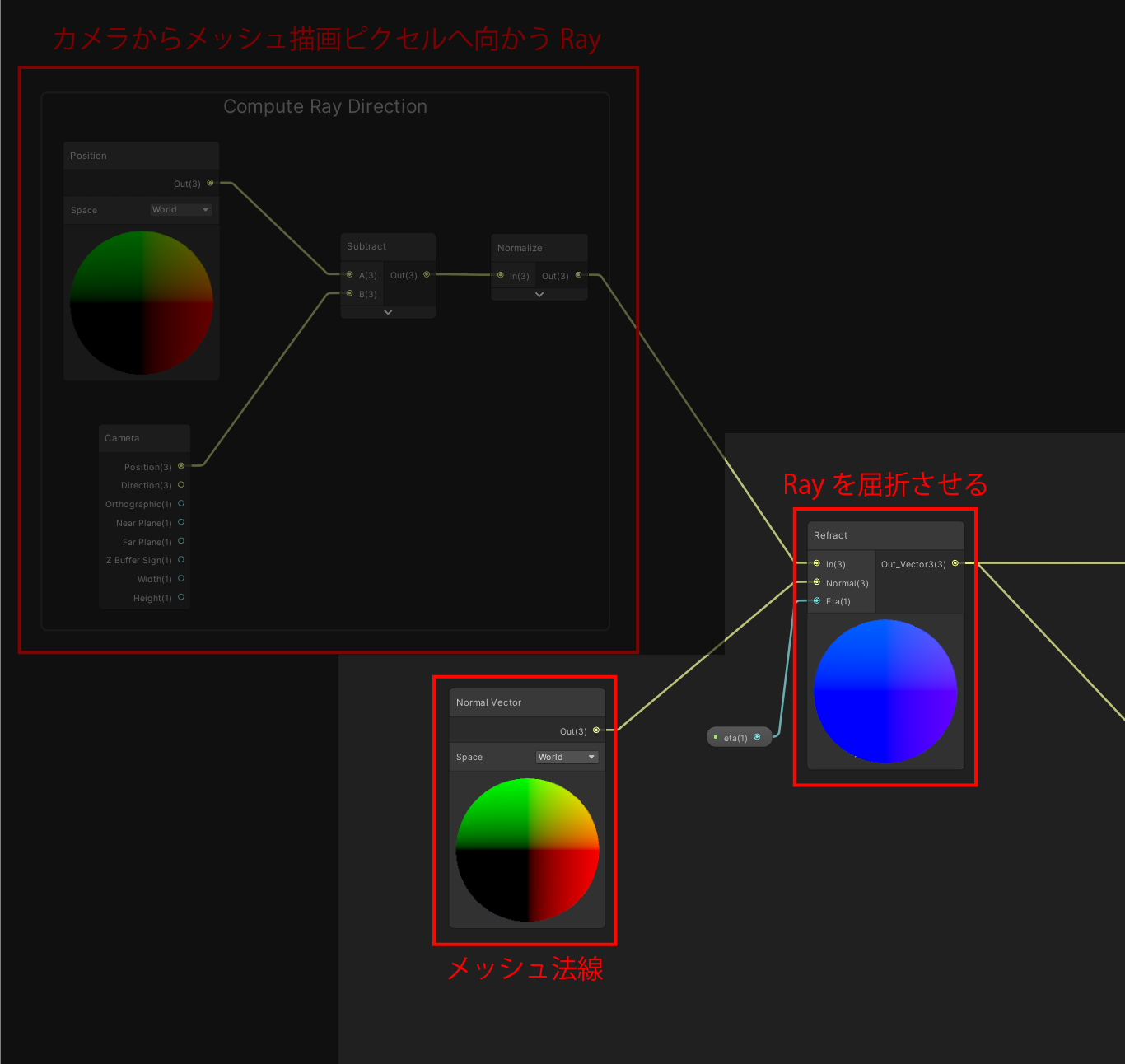
Ray向きの計算部分

Rayの屈折部分

ここではメッシュ法線を利用して、Rayの向きを屈折させています。

カスタムノード Refract

ShaderGraphには屈折させるノードは存在しないので、カスタムノードでRefract(屈折)ノードを作成しました。

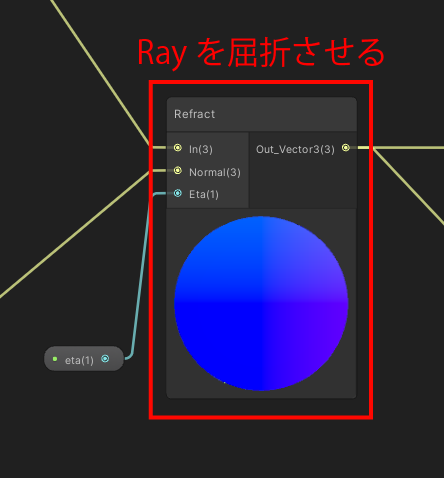
カスタムノード Refractの実装について

## カスタムノード Refractの実装 カスタムノードの中身では、Custom Functionで屈折処理を実装しています。 

Refract

OutDir = refract(RayDir, Normal, eta);

RayDir, Normal について

RayDirはRayの向き、NormalはRayとメッシュが当たる位置の法線Nです。

etaについて

etaは屈折率の比を表しています。
空気(1.0)から水(1.333)へ入射する場合、はeta = 0.75になります。

eta = \frac{1.0}{1.333} \approx 0.75

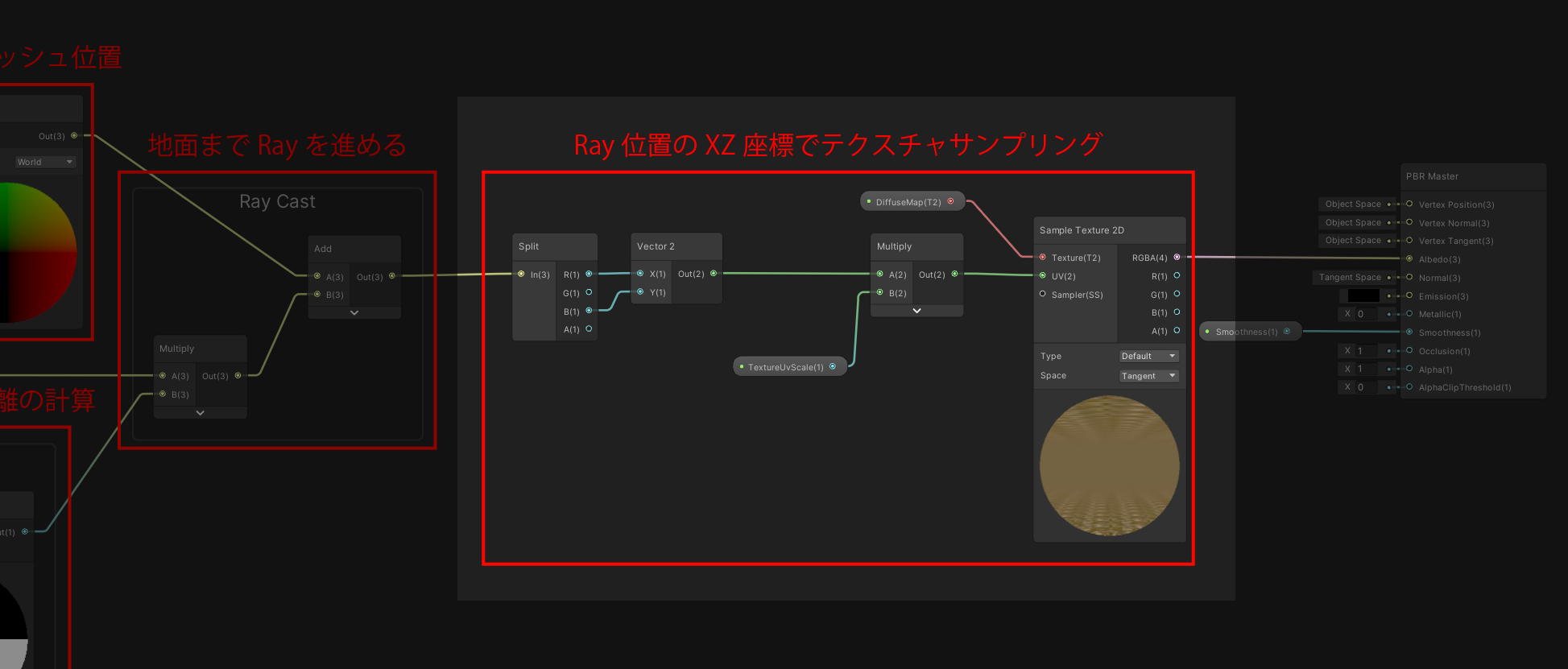
Rayの進む距離の計算部分

ここでは、Rayが地面にぶつかるまでの距離を計算しています。

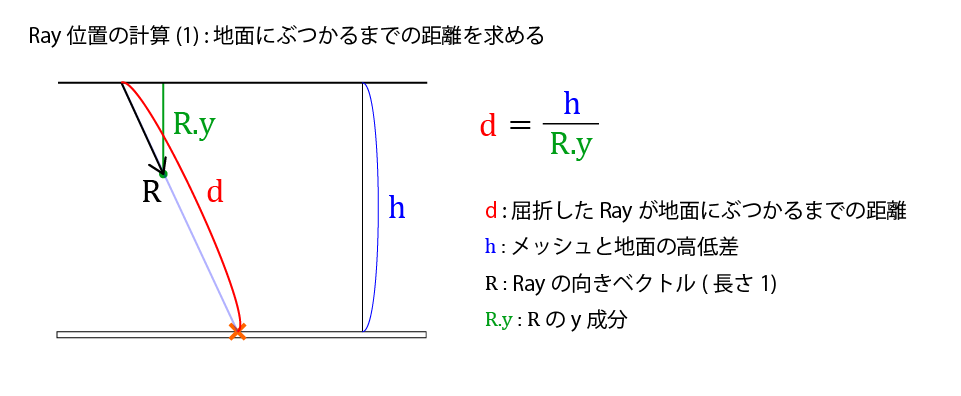
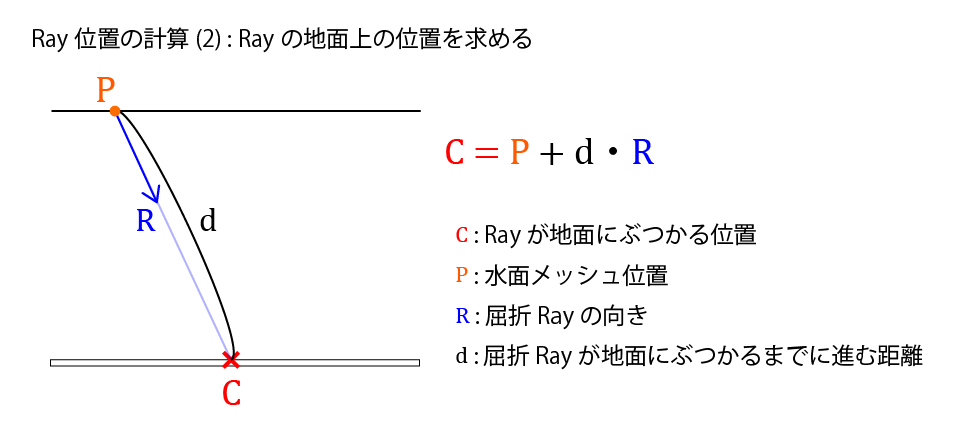
Ray位置の計算

ここでは、Rayの地面上の位置を計算しています。

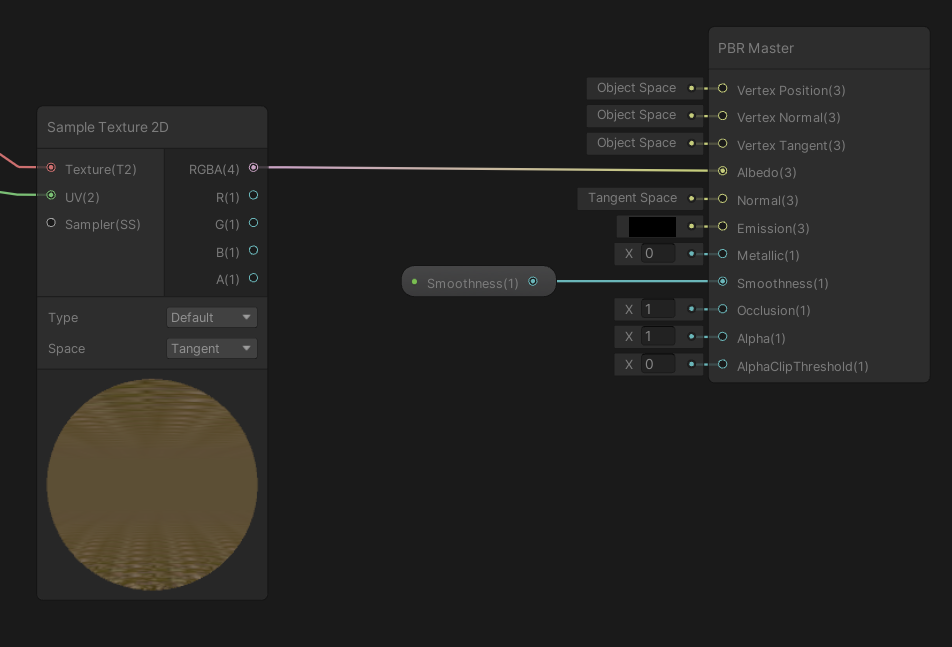
地面テクスチャサンプリング処理

地面のRayのXZ座標を使って地面テクスチャをサンプリングしています。

サンプリング結果は、Albedoとして出力します。

結果