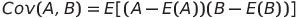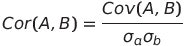Fundamental Statistics for Data Science (Part 03)

This article is a continuation of Fundamental Statistics for Data Science (Part 02).

1. Covariance
   Covariance measures the relationship among two random variables. Let's assume that we have two random variables, A and B. Where respectively E(A) and E(B) represent the means of the A and B.

Covariance values can be 0, positive or negative. A negative value indicates the variable varies in the opposite direction, and if the value is positive, two random variables vary in the same direction. And if the value is 0, then the variable not varies together.

cor_var.py

import numpy as np

a = np.array([2,4,7,8])
b = np.array([-1,-2,-4,-7])

ab_cov = np.cov(a,b)
print(ab_cov)

1. Correlation

This also measures the relationship between two random variables. Correlation coefficients values reside between -1 to 1. Correlation of variable with its self always 1. Cor(A, A) = 1 . And also, it is critical to remember even there is a correlation between two random variables, it's not necessary to change one variable cause to change the other. There might be another variable that causes both variables to change.

we can calculate the correlation coefficient by,

cor_var.py

import numpy as np

a = np.array([2,4,7,8])
b = np.array([-1,-2,-4,-7])
corr = np.corrcoef(a, b)

print(corr)

There are different correlation calculation methods such as;

• pearson
• spearman
• kendall

Some example that we use correlation.

• How the height of soccer players is correlated to their shooting strength.
• Is there any relationship between employee work experience and salary.

In the next part, lets' talk about probability distribution functions.

*本記事は @qualitia_cdevの中の一人、@nuwanさんが書いてくれました。
*This article is written by @nuwan a member of @qualitia_cdev.