LoginSignup
21
25

More than 3 years have passed since last update.

@ps010(cyumizou)inSupership株式会社

データ拡張：少数データをSMOTEで増やしてみる

Last updated at Posted at 2020-03-26

はじめに

機械学習をビジネスで使う場合、学習データが十分に準備できないことがままあります。
私のチームでも、デジタル広告を閲覧して購入するユーザーを二値分類するときに、正例の購入ユーザーのデータが十分にないことがあり、過学習による汎化性能の低下（＝精度低下）が課題となっています。

こうした少数データのモデルの精度を改善するアプローチに 「データ拡張（Data Augmentation）」 という技術があります。データ拡張は、学習データに変換を加えてデータ量を増やす技術で、構造化データ、画像、音声など幅広い分野に適用されています。

データ拡張は、データの種別によってアプローチが異なり、

  • 構造化データ： 不均衡データの調整でSMOTEがよく用いられる
  • 画像データ： コンピュータービジョンや深層学習の画像加工ライブラリが主流
  • 音声データ： 周波数データに変換し、水増し加工（移調、1分ごとに区切る等）

などが使われています。
今回は、構造化データのデータ拡張の一種 「SMOTE」 について調べ、実験してみようと思います。

SMOTEの概要

SMOTE(Synthetic Minority Oversampling Technique)は、不均衡データの少数派データを増やす Oversampling の一種です。
少数派のラベルが付いたデータをそのまま複製するのではなく、KNNを用いて増やします。
検出した少数派の近接データを線でつなぎ、その線分上の任意の点を人工データとしてランダムに生成します。

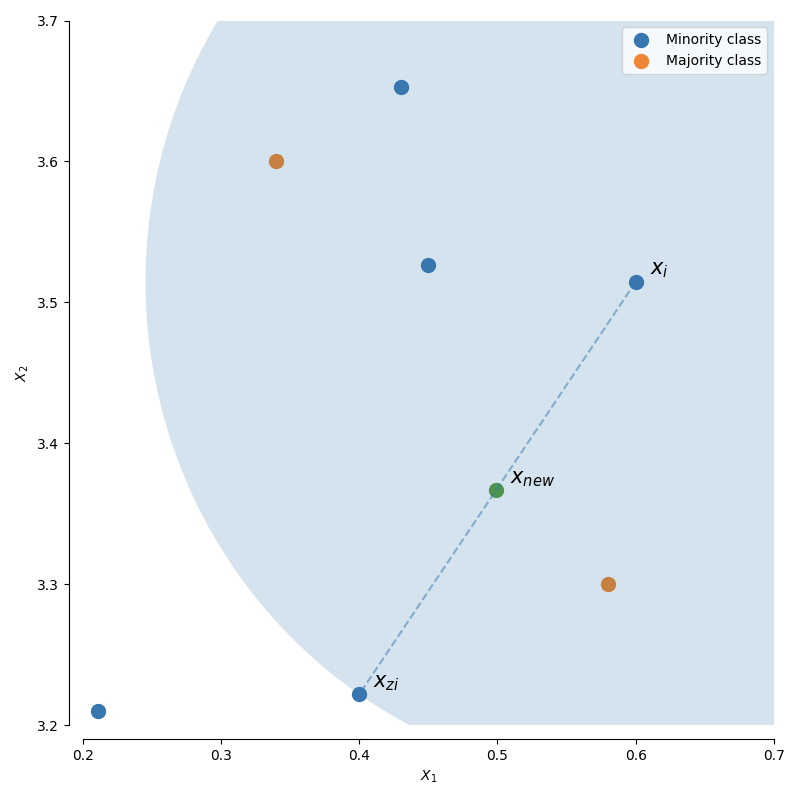
ユーザーガイドの図1がわかりやすいので、抜粋しました。
まず初期のデータ点 Xi が選ばれます。次に近傍3つからランダムに Xziが選ばれ、2つの線分上の任意の点 Xnewが生成されます。これが基本ロジックです。
image.png

拡張のタイプ

SMOTEには多くの拡張版が出ています。
15年記念に発表された論文2によると、拡張方針には次の7つが見られるそうです。

  1. Oversamplingする初期のデータ点の選び方（境界が近いか否か、近傍の少数派の数など）
  2. Undersamplingとの統合
  3. 補間範囲の制限をどう決定するか（近傍の特定手法など）
  4. 次元変化を伴う操作をどの段階で行うか
  5. 人工データ生成に、適応的な手法を用いるか否か
  6. どのデータ点を再ラベルづけするか
  7. ノイズ除去のフィルタリングステップを入れるか否か

今回実験する、4つの代表的な手法

  • SMOTE
  • Adasyn
  • Boderline SMOTE
  • SMOTEENN

は、1・2・5・7の方針に関係があるものです（Adasynは1・5、Boderlineは1、SMOTEENNは2・7）。
今回は、それぞれのアプローチの違いと精度に与える影響を見てみたいと思います。

試してみる

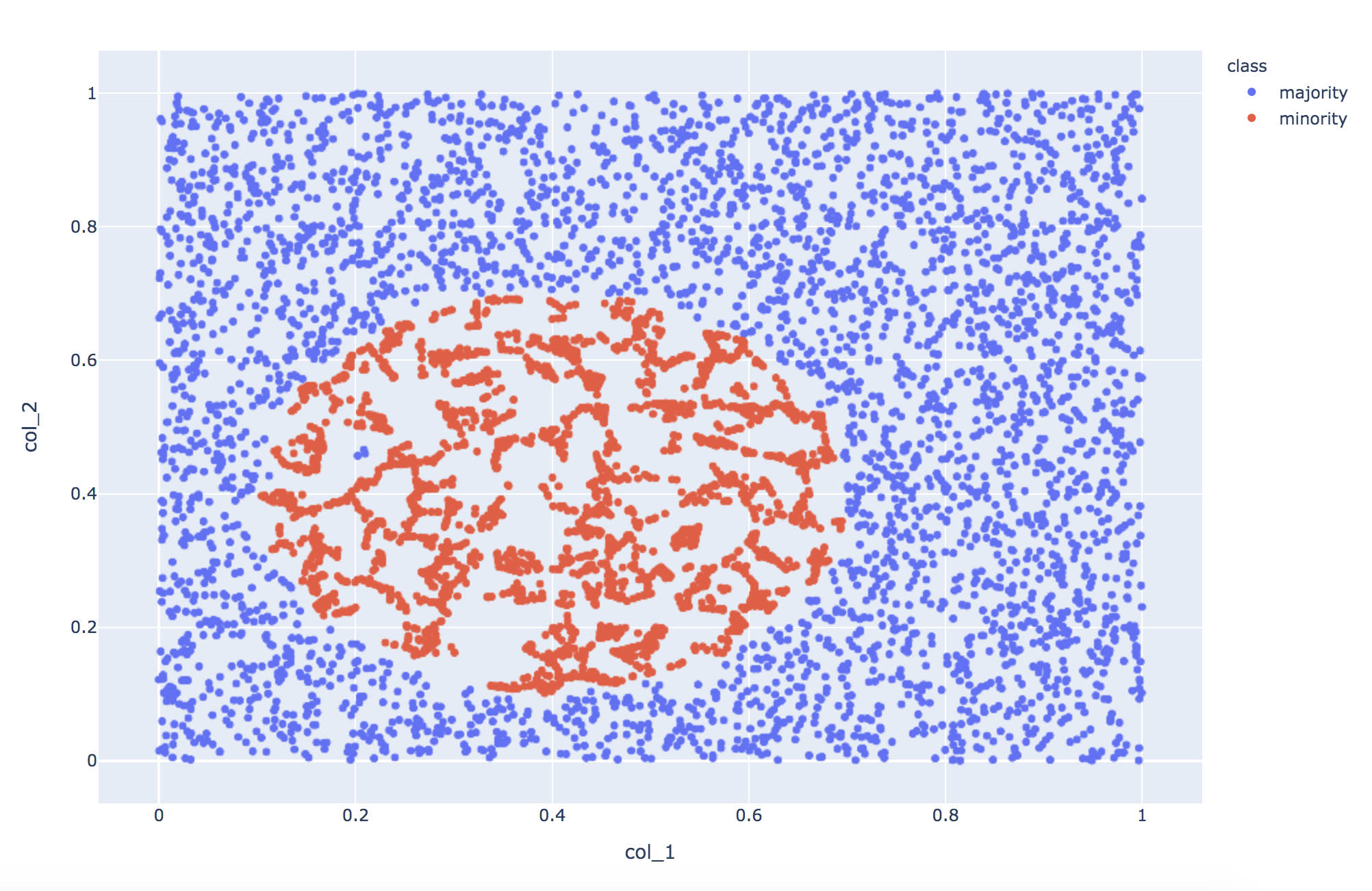
今回は、こちらのサイト3を参考にして不均衡データを作りました。拡張方針による挙動の違いがわかりやすいように、分布を調整しています。
不均衡データの二値分類はLightGBMで作りました。

データ作成のサンプルコード
サンプルデータ
import numpy as np
import random
import pandas as pd

# 元データ
Ndata = 7000
data = np.random.rand(Ndata, 2)

x = data[:,0]
y = data[:,1]
z = np.power(x-0.4,2) + np.power(y-0.4,2)

# 少数派データを作る
## 少数派エリアのデータを収集
data_minor_flg     = np.insert(data, 2, z, axis=1)
data_minor         = data_minor_flg[data_minor_flg[:,2] < 0.3**2][:,0:2]
data_minor_li      = data_minor.tolist()

## 少数派エリアをランダムサンプリング
len_data_for_minor = round(len(data_minor) * 0.4)
data_minor_sampled = random.sample(data_minor_li, len_data_for_minor)
Data_minor         = set(map(tuple, data_minor_li))
Data_minor_samp    = set(map(tuple, data_minor_sampled))

## 少数派データにフラグを付与
data_minor_arr         = np.array(list(Data_minor_samp))
Data_minor_pd          = pd.DataFrame(data_minor_arr)
Data_minor_pd          = Data_minor_pd.rename(columns={0: 'col_1', 1: 'col_2'})
Data_minor_pd['class'] = 1
print('Minority: ', len(data_minor_arr))

# 多数派データを作る
## 多数派エリアのデータを収集
data_li = data.tolist()
Data    = set(map(tuple, data_li))

## 少数派エリアに混ぜる多数派データを用意
len_data_for_data    = round(len(data_minor) * 0.15)
data_sampled         = random.sample(data_minor_li, len_data_for_data)
Data_samp_for_data   = set(map(tuple, data_sampled))
Data_wo_minor        = Data.difference(Data_minor)
Data_wo_minor_w_samp = Data_wo_minor | Data_samp_for_data

## 多数派データにフラグを付与
data_arr         = np.array(list(Data_wo_minor_w_samp))
Data_pd          = pd.DataFrame(data_arr)
Data_pd          = Data_pd.rename(columns={0: 'col_1', 1: 'col_2'})
Data_pd['class'] = 0
print('Majority: ',len(data_arr))

# データの保存
Data_all_pd = Data_minor_pd.append(Data_pd, ignore_index=True)
path = './data/sample_data.csv'
Data_all_pd.to_csv(path, index=False)
print('Total: ', Data_all_pd['class'].count())

LigthGBMサンプルコード
データ整形／LigthGBMの計算
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
import lightgbm as lgb
import pandas as pd
import plotly.express as px

# データ取得
path           = '/Users/somebody/data/sample_data.csv'
df_samp        = pd.read_csv(path)
df_samp_sorted = df_samp.sort_values('class')

# 行列を作る
X_origin = df_samp_sorted.drop('class', axis=1)
y_origin = df_samp_sorted['class']

# 学習用と検証用に分ける
X, y, X_test, y_test = train_test_split(X_origin, y_origin)

# LightGBMの計算
def run_lgb(X_train, y_train, X_test, y_test):
    # データセットを生成する
    lgb_train = lgb.Dataset(X_train, y_train)
    lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)
    # LightGBM のハイパーパラメータ
    lgbm_params = {
        # 二値分類問題
        'objective': 'binary',
        'boosting_type': 'gbdt',
        'metric': 'logloss',
    }
    # モデルを学習する
    model = lgb.train(lgbm_params, lgb_train, valid_sets=lgb_eval)
    # テストデータを予測する
    y_pred = model.predict(X_test, num_iteration=model.best_iteration)
    return y_test, y_pred

# LightGBMの適用
y_test, y_pred = run_lgb(X, y, X_test, y_test)
結果出力
# 散布図の描画
y = y.replace({1: 'minority', 0: 'majority'})
origin = pd.concat([X, y], axis=1)
fig    = px.scatter(origin, x='col_1', y='col_2', color='class')
fig.show()

# 精度の計算
print('Accuracy score  = \t {}'.format(accuracy_score(y_test, y_pred.round())))
print('Precision score = \t {}'.format(precision_score(y_test, y_pred.round())))
print('Recall score    = \t {}'.format(recall_score(y_test, y_pred.round())))
print('F1 score        = \t {}'.format(f1_score(y_test, y_pred.round())))

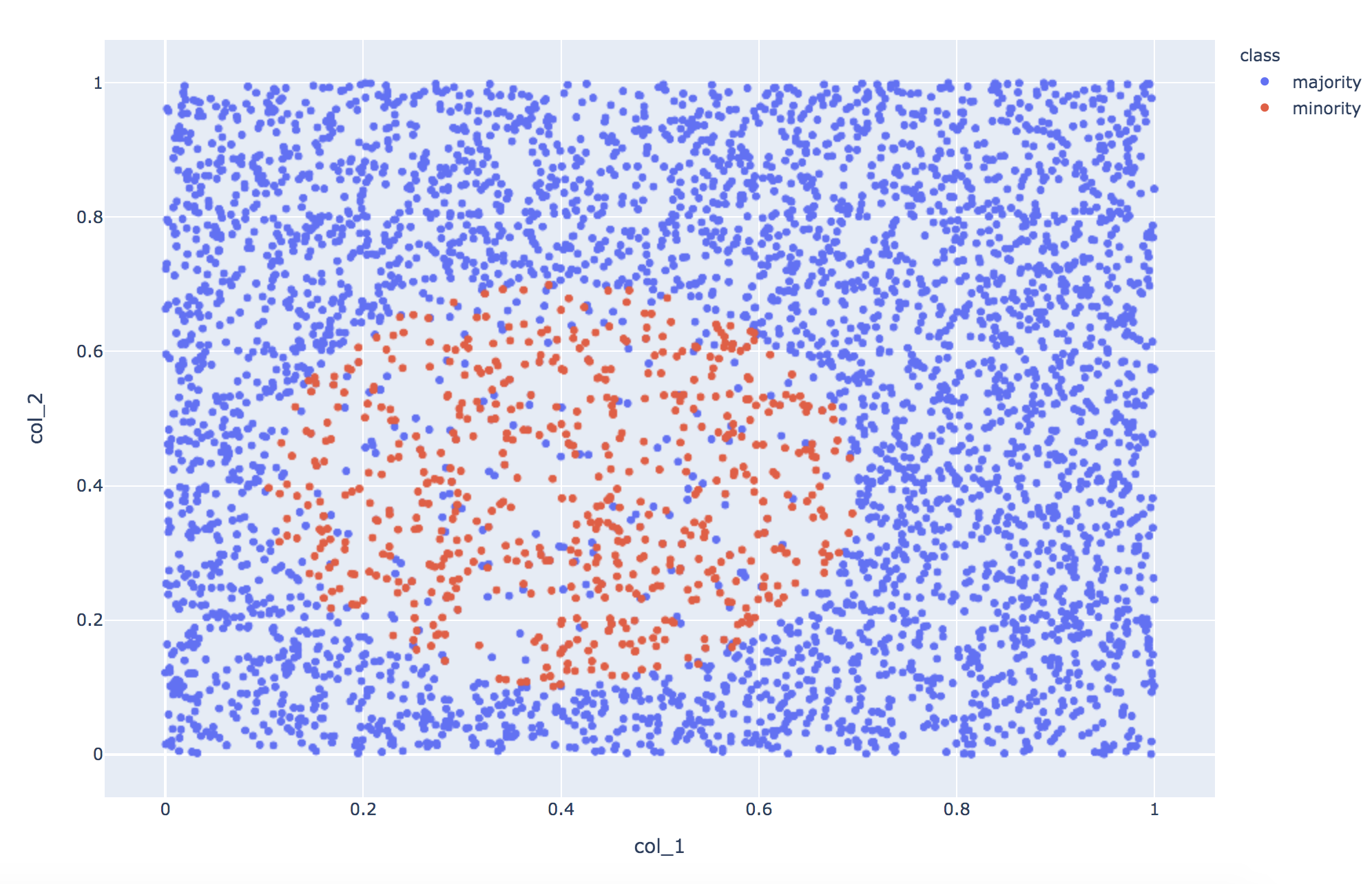
Original

作成したデータがこちら。
image.png

少数派データは多数派のおよそ8分の1とし、エリアを分けました。
少数派エリアに多数派を混ぜてます。

Originalデータの学習結果は、F1 scoreで0.74です。Recallが高め。
このデータをベンチマークにして比較をしていきます。
なお、検証用データは全種類でOriginalと同じものを使用します。

Originalの結果
X_trainの形 (4591, 2)     少数派の数 590     多数派の数 4001
Accuracy score =     0.9261920313520575
Precision score =    0.7033898305084746
Recall score =       0.7942583732057417
F1 score =           0.7460674157303372

SMOTE

では、SMOTEを適用してみましょう。

SMOTE適用のサンプルコード
SMOTEの適用
from imblearn.over_sampling import SMOTE

sm = SMOTE(sampling_strategy='auto', k_neighbors=5, random_state=71)
X_smote, y_smote = sm.fit_sample(X, y)
print('Xの形',X_smote.shape,'\t少数派の数', y_smote[y_smote=='minority'].count(),'\t多数派の数', y_smote[y_smote=='majority'].count())

結果はこちら。
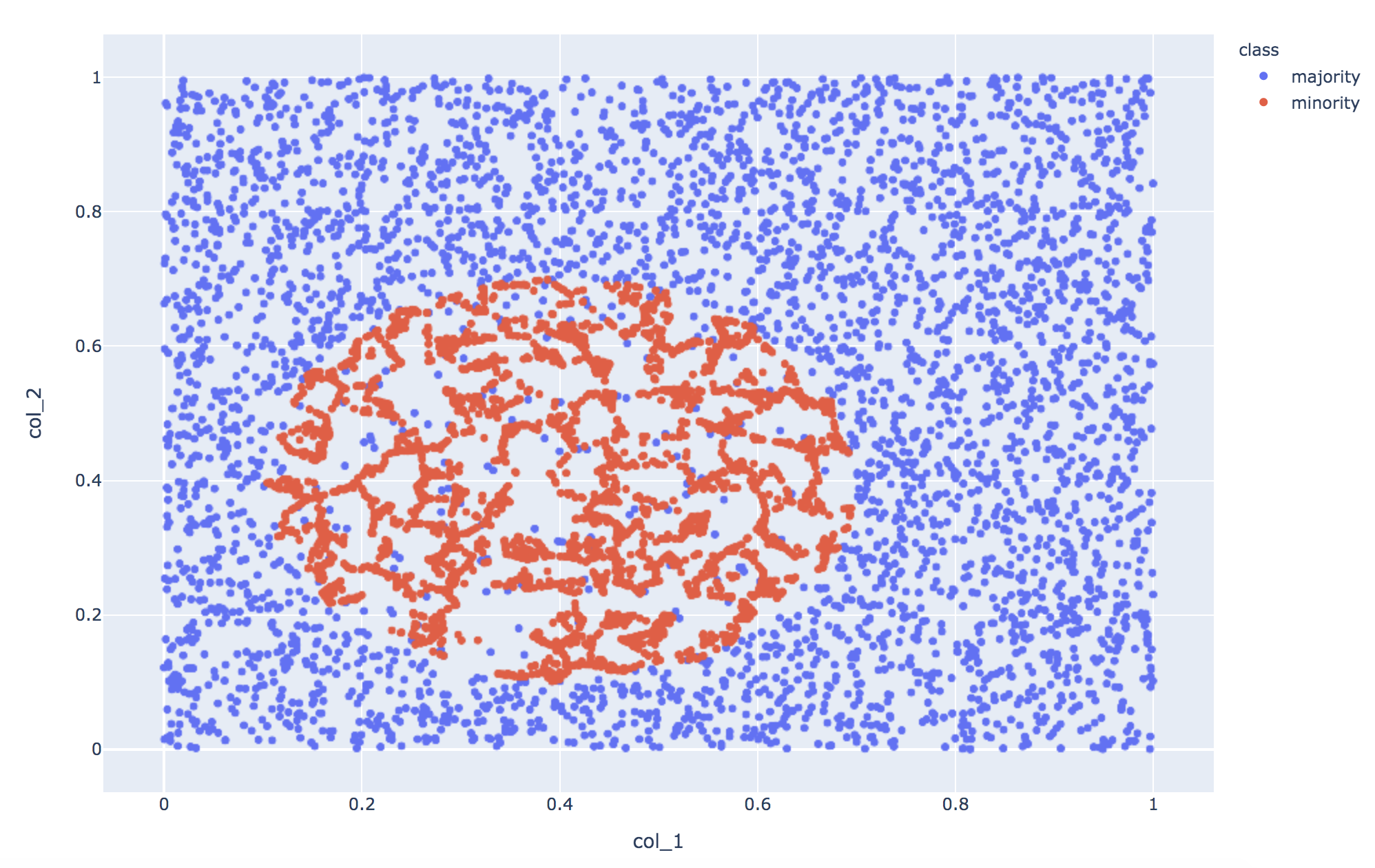
image.png

少数派が分布するところに、満遍なくデータが補間されました。
モデルの精度は、Recallが改善した影響でF1 scoreが0.81になりました。

SMOTEの結果
X_trainの形 (8002, 2)     少数派の数 4001    多数派の数 4001
Accuracy score =     0.9412148922273024
Precision score =    0.7148014440433214
Recall score =       0.9473684210526315
F1 score =           0.8148148148148149

Adasyn

次にAdasyn（Adaptive Synthetic）。
Oversamplingする初期のデータ点は、周囲に多数派データの比率が多いものが選ばれます。

Adasyn適用のサンプルコード
Adasynの適用
from imblearn.over_sampling import ADASYN

ada = ADASYN(random_state=71)
X_ada, y_ada = ada.fit_resample(X, y)
print('Xの形',X_ada.shape,'\t少数派の数', y_ada[y_ada=='minority'].count(),'\t多数派の数', y_ada[y_ada=='majority'].count())

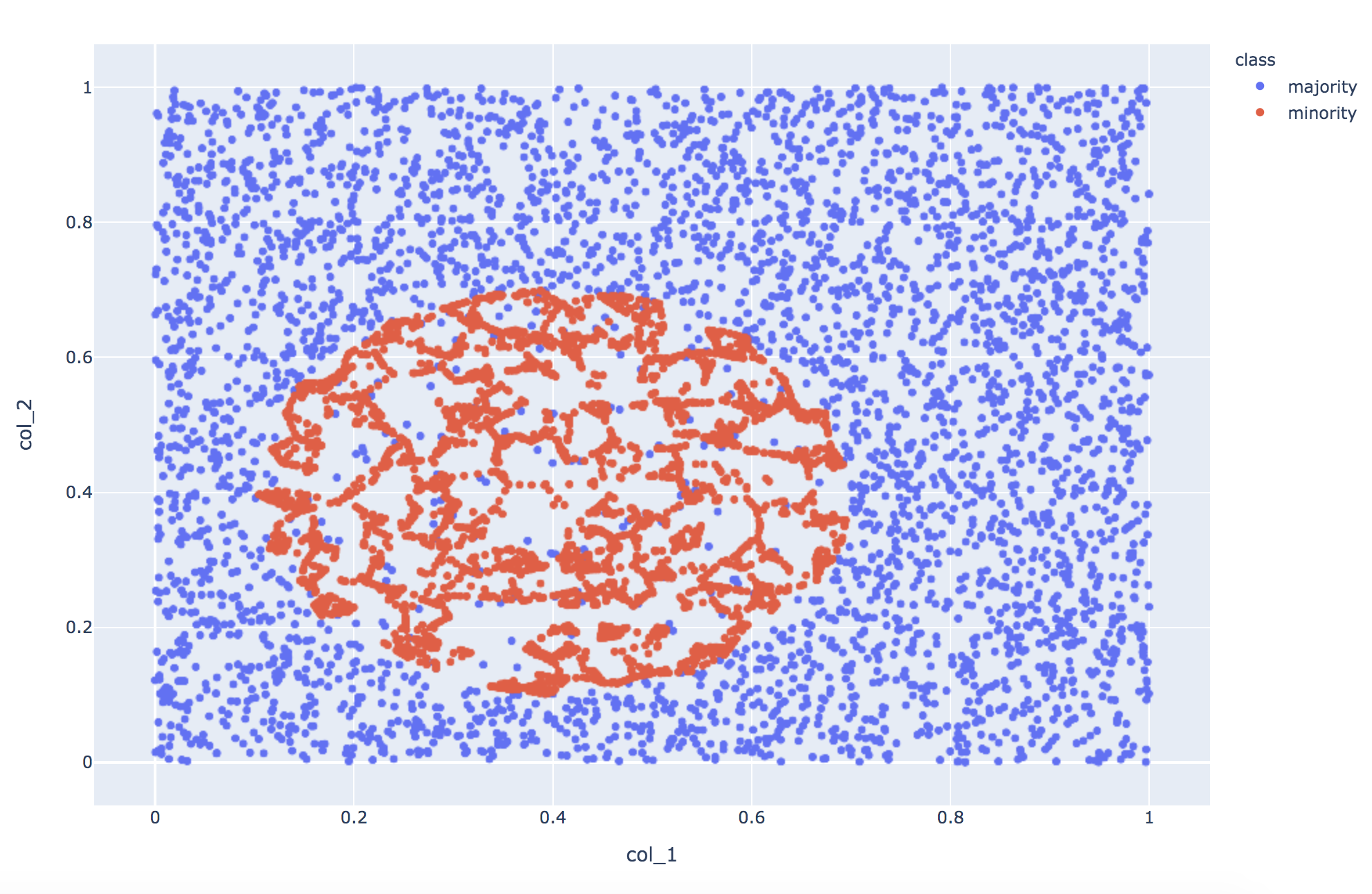
image.png

SMOTEと分布を比較すると、エリアの境界付近により多くの少数派データが生成されています。
精度の改善度合いはSMOTEとほぼ同じで、F1 scoreは0.82となりました。

Adasyn_LightGBMの結果
X_trainの形 (8151, 2)     少数派の数 4150    多数派の数 4001
Accuracy score =     0.9438275636838668
Precision score =    0.7236363636363636
Recall score =       0.9521531100478469
F1 score =           0.8223140495867769

Boderline SMOTE

Boderline SMOTEは、少なくとも近傍の半分が多数派になるデータ点 Xi をOversamplingします。
種類が2つあり、Borderline1は同じ少数派クラス Xzi との内分点にデータを生成し、Borderline2はXziのクラスを考慮しません。
今回は、デフォルトのBorderline1を試します。

Boderline SMOTE適用のサンプルコード
BoderlineSMOTEの適用
from imblearn.over_sampling import BorderlineSMOTE

blsm = BorderlineSMOTE(sampling_strategy='auto', k_neighbors=5, random_state=71, kind='borderline-1')
X_blsmote, y_blsmote = blsm.fit_sample(X, y)
print('Xの形',X_blsmote.shape,'\t少数派の数', y_blsmote[y_blsmote=='minority'].count(),'\t多数派の数', y_blsmote[y_blsmote=='majority'].count())

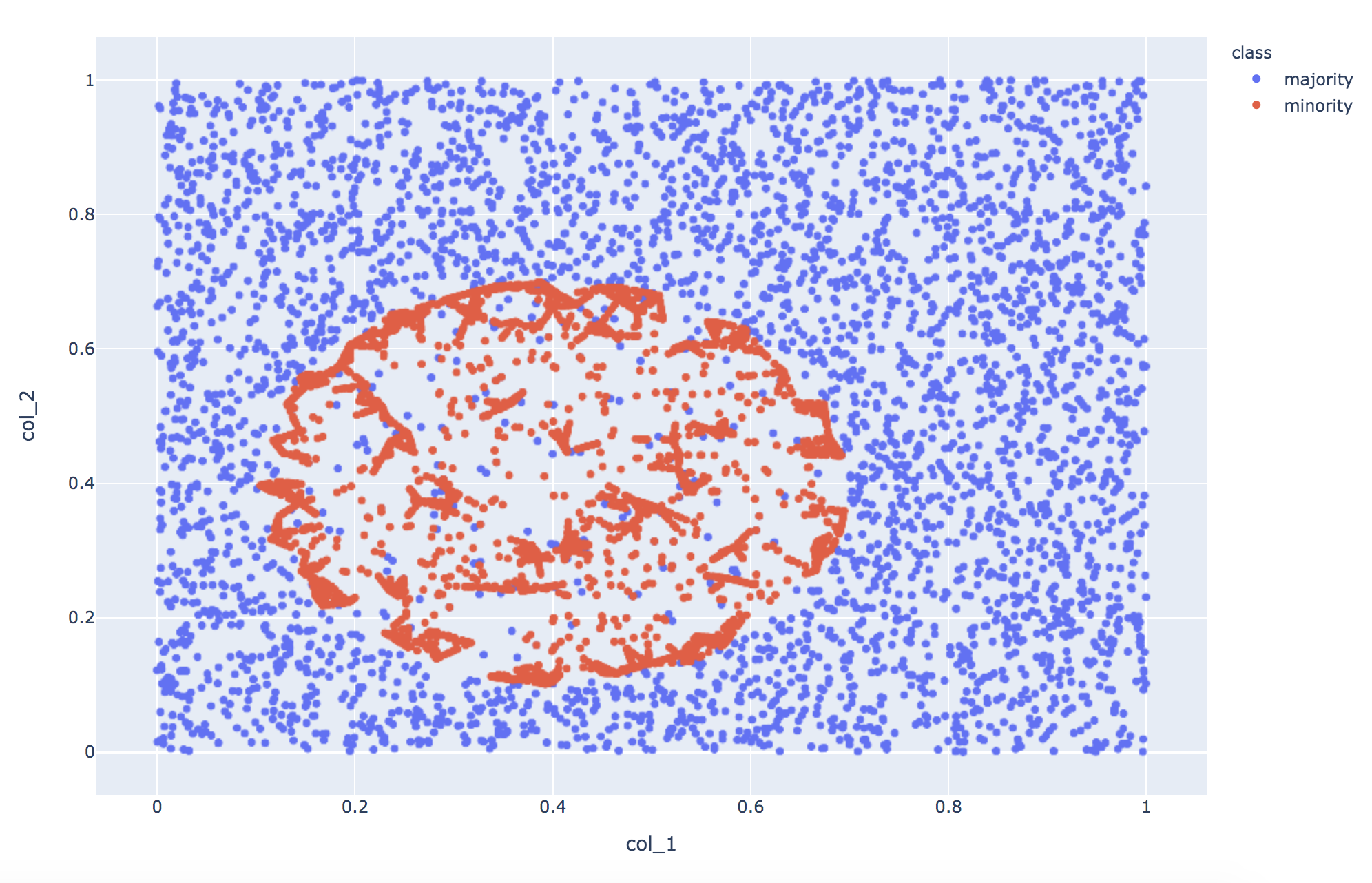
image.png

Adasynと分布を比較すると、少数派エリアの中央への補間が減りました。
精度はSMOTEやAdasynとほぼ同じで、F1 score は0.82でした。

BorderlineSMOTE_LightGBMの結果
X_trainの形 (8002, 2)     少数派の数 4001    多数派の数 4001
Accuracy score =     0.9444807315480078
Precision score =    0.7262773722627737
Recall score =       0.9521531100478469
F1 score =           0.8240165631469979

SMOTEENN

最後にSMOTEENN。
これはOversamplingのSMOTEと、Undersampling の ENN（Edited Nearest Neighbours）を組み合わせたものです。ENNは、近傍に少数派しか存在しない多数派データ（ノイズ）をフィルタリングします。
結果はこちら。

SMOTEENN適用のサンプルコード
SMOTEENNの適用
from imblearn.combine import SMOTEENN

smtn = SMOTEENN(sampling_strategy='auto', random_state=71)
X_smoteenn1, y_smoteenn1 = smtn.fit_sample(X, y)
print('Xの形',X_smoteenn1.shape,'\t少数派の数', y_smoteenn1[y_smoteenn1=='minority'].count(),'\t多数派の数', y_smoteenn1[y_smoteenn1=='majority'].count())

image.png

少数派の分布はSMOTEと同じです。
少数派エリアの多数派データはノイズと見做され、削除されています。
精度は他の手法と変わらず、F1 scoreが0.81となりました。

SMOTEENN_LightGBMの結果
X_trainの形 (7261, 2)     少数派の数 3550    多数派の数 3711
Accuracy score =     0.9405617243631613
Precision score =    0.7048611111111112
Recall score =       0.9712918660287081
F1 score =           0.8169014084507042

まとめ

実験の結果、4つの手法の精度改善の度合いは、ほぼ同じでした（平均+0.075）。

種類 F1 score Originalとの差
Original 0.74 -
SMOTE 0.81 +0.07
Adasyn 0.82 +0.08
Boderline SMOTE 0.82 +0.08
SMOTEENN 0.81 +0.07

いずれも、Recallが改善した影響で、F1 scoreが上昇しています。
グラフを比較すると、拡張方針によって少数派と多数派の違いをどう強調するのか、アプローチが違うことがわかります。多数派のノイズが多い場合はSMOTEENNの効果が高く、多数派と少数派の塊が入り組んで分布する場合はAdasynとBorderlineが効きそうです。

以上のことから、データ拡張による精度改善は期待できそうです。
ただし、データの分布によって、改善度合いやどのタイプが効くかが異なるようなので、保有データの分布状況に合った拡張版を選ぶ必要があると思われます。

参考サイト

解説編：オーバーサンプリング手法解説 (SMOTE, ADASYN, Borderline-SMOTE, Safe-level SMOTE)
【ML Tech RPT. 】第4回 不均衡データ学習 (Learning from Imbalanced Data) を学ぶ(1)
imbalanced-learnの機能の紹介
不均衡データの学習 ~imblanced-learnを例に~
【前処理の学習-35】データを学ぶ〜生成〜③

  1. SMOTE User guide > Sample generation ↩

  2. SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-year Anniversary ↩

  3. 実装編：オーバーサンプリング手法比較 (SMOTE, ADASYN, Borderline-SMOTE, Safe-level SMOTE) ↩

21
25
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
21
25