LoginSignup
1
1

More than 1 year has passed since last update.

@pocokhc(ちぃがぅ)

tf.GradientTapeで正則化項が反映されているか調査してみた（過学習の公式チュートリアルを添えて）

Posted at

Tensorflowでモデルを学習する場合、fit関数を使う場合が多いと思います。
しかし、学習内容が特殊だったりカスタマイズしたい場合に tf.GradientTape により独自にlossを計算したい場合があるかと思います。
その場合、正則化項ってどうなってるの？と思い検証してみました。

基本は以下の公式チュートリアルを参考に作成しています。
TensorFlow > 学ぶ > TensorFlow Core > チュートリアル > 過学習と学習不足について知る

データセット

チュートリアルのデータセットと同じです。
過学習しやすいデータセットのようでチュートリアルでも詳細には触れていません。
(素粒子物理学に関するデータだとか)

元データは 11,000,000 あるそうで、全データを使うと時間が足りません。
なので検証用に最初の1000データを使い、トレーニング用にその後の10,000データを使っています。
特徴量は28個あり、正解ラベルは0か1の2値分類です。

以下コードです。

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow.keras.layers as kl

# --- ダウンロード
gz = tf.keras.utils.get_file('HIGGS.csv.gz', 'http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz')

# --- 固定値
FEATURES = 28  # 特徴量
N_VALIDATION = int(1e3)  # 検証用データ数
N_TRAIN = int(1e4)       # 学習用データ数
BUFFER_SIZE = int(1e4)
BATCH_SIZE = 500    # バッチサイズ
STEPS_PER_EPOCH = N_TRAIN//BATCH_SIZE  # 1エポックあたりの学習回数
MAX_EPOCHS = 100    # 学習回数（ここはチュートリアルと変えています）

# --- 以下公式のコードをコピペして改変
ds = tf.data.experimental.CsvDataset(gz,[float(),]*(FEATURES+1), compression_type="GZIP")

def pack_row(*row):
  label = row[0]
  features = tf.stack(row[1:],1)
  return features, label
packed_ds = ds.batch(10000).map(pack_row).unbatch()

for features,label in packed_ds.batch(1000).take(1):
  print(features[0])
  plt.hist(features.numpy().flatten(), bins = 101)

# trainデータセットとvalidデータセットを作成
validate_ds = packed_ds.take(N_VALIDATION).cache().batch(BATCH_SIZE)
train_ds = packed_ds.skip(N_VALIDATION).take(N_TRAIN).cache().shuffle(BUFFER_SIZE).repeat().batch(BATCH_SIZE)

損失関数(loss)、optimizer、メトリック(metric)

以下を使います。
チュートリアルでは学習率をエポック数に合わせて減少させていますが本質ではないので本記事では固定にしています。

loss_func = keras.losses.BinaryCrossentropy(from_logits=True)
optimizer = keras.optimizers.legacy.Adam(learning_rate=0.001)
metric = keras.metrics.BinaryAccuracy()

lossは2値分類なのでバイナリクロスエントロピーです。
OptimizerはAdam、metricは正解率（閾値0.5）を使っています。

基本となる学習・検証コード

チュートリアルの大規模モデルをベースとして見ていきます。
モデルは以下です。

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(1),
])
model.compile(optimizer=optimizer, loss=loss_func, metrics=[metric])

学習コードは以下です。

history = model.fit(
    train_ds,
    epochs=MAX_EPOCHS,
    steps_per_epoch=STEPS_PER_EPOCH,
    validation_data=validate_ds,
)

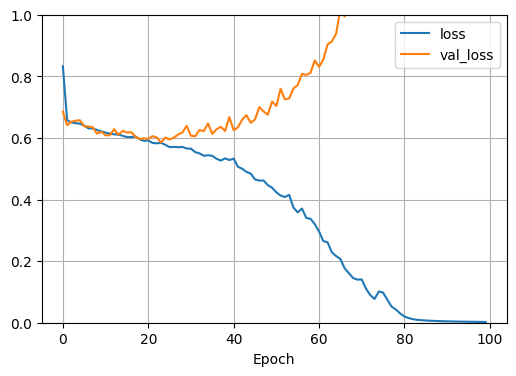
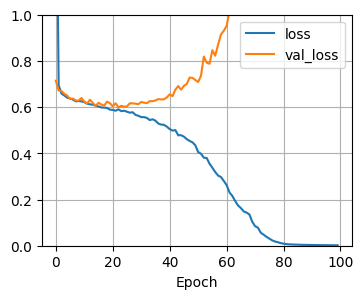
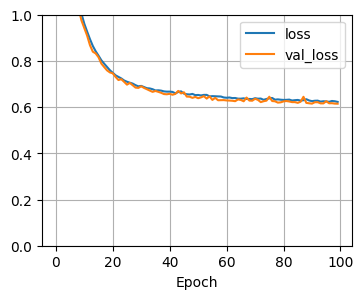
学習結果です。

plt.figure(figsize = (6,4))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.ylim([0, 1])
plt.grid()
plt.legend()
plt.xlabel('Epoch')
plt.show()

plt.figure(figsize = (6,4))
plt.plot(history.history["binary_accuracy"], label="acc")
plt.plot(history.history["val_binary_accuracy"], label="val_acc")
plt.ylim([0, 1])
plt.grid()
plt.legend()
plt.xlabel('Epoch')
plt.show()

output1.png
output2.png

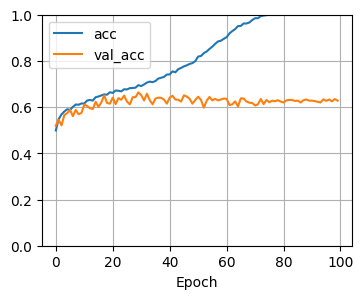
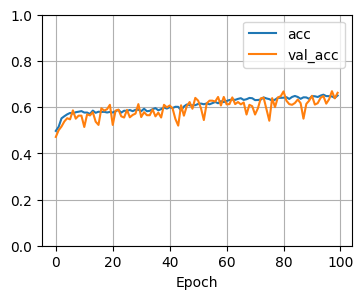
青が学習データでオレンジが検証データの結果です。
青のlossは最適解（0方向）になっていますが、検証データでは逆に悪く（1方向）になっていますね。
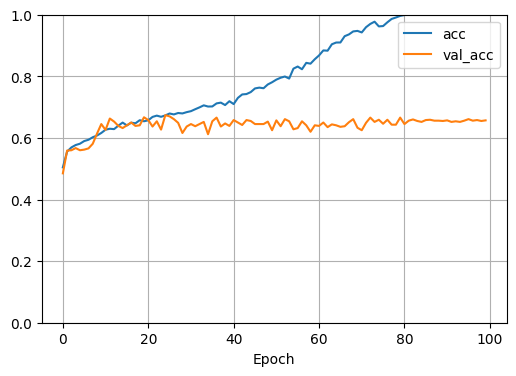
正解率も青のaccはほぼ1.0（100%正解）になっていますが、検証データではそんなことにはなっていません。

これは典型的な過学習の傾向ですね。

正則化項を加えると過学習を抑えれるよ

チュートリアルは過学習を抑える手法の１つとして正則化項の追加が紹介されています。
（他にはドロップアウト層の追加など）

L2正則化項を追加した場合を見てみます。

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(1),
])
model.compile(optimizer=optimizer, loss=loss_func, metrics=[metric])

学習コードと結果のコードは同じです。（一応載せておきます）

history = model.fit(
    train_ds,
    epochs=MAX_EPOCHS,
    steps_per_epoch=STEPS_PER_EPOCH,
    validation_data=validate_ds,
)
plt.figure(figsize = (6,4))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.ylim([0, 1])
plt.grid()
plt.legend()
plt.xlabel('Epoch')
plt.show()

plt.figure(figsize = (6,4))
plt.plot(history.history["binary_accuracy"], label="acc")
plt.plot(history.history["val_binary_accuracy"], label="val_acc")
plt.ylim([0, 1])
plt.grid()
plt.legend()
plt.xlabel('Epoch')
plt.show()

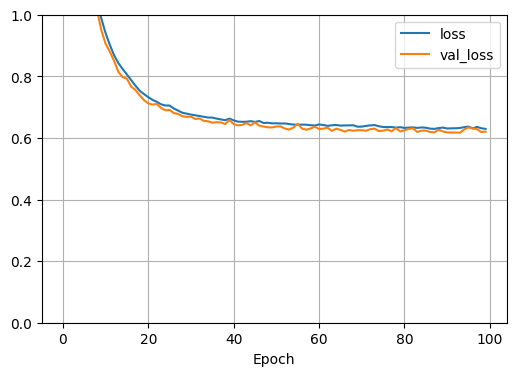
output3.png
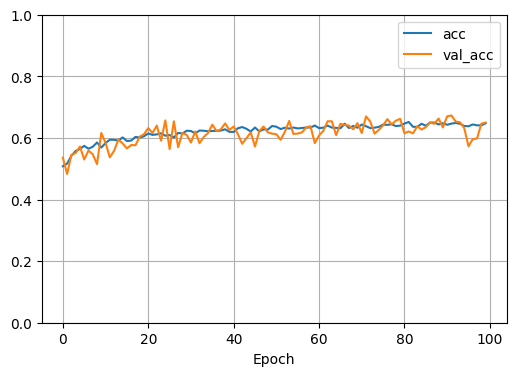
output4.png

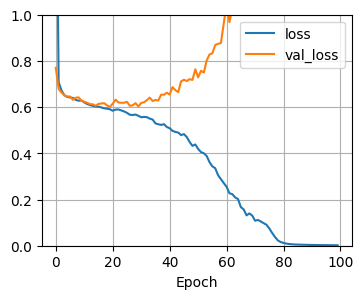
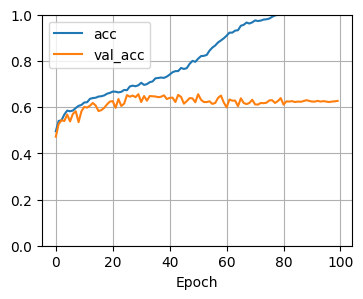
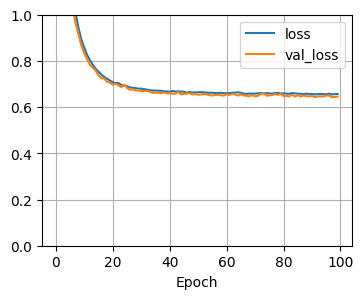
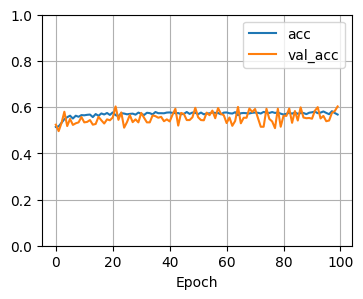
lossとacc両方で青とオレンジが同じ傾向になりましたね。
過学習が抑えられていることが分かります。

fitを使わずにtf.GradientTapeで手動で学習する場合

特殊な勾配を計算する場合 tf.GradientTape を使って、カスタマイズした勾配計算をしたい場合があると思います。（主に強化学習）

fit の内容を tf.GradientTape で書いて見ると以下のコードになります。
（loss_func,optimizer,metric は同じものを使っています）

#from tqdm import tqdm
from tqdm.notebook import tqdm

def fit(model, add_normalize_loss: bool):

    # --- 学習ループ
    loss_list = []
    acc_list = []
    val_loss_list = []
    val_acc_list = []
    for epoch in tqdm(range(MAX_EPOCHS)):

        # --- 1epochのループ
        epoch_loss_list = []
        metric.reset_state()
        for step, (x, y_true) in enumerate(train_ds):
            # 勾配を計算
            with tf.GradientTape() as tape:
                y_pred = model(x, training=True)
                loss = loss_func(y_true, y_pred)

                # --- 正則化項を加えるコード
                if add_normalize_loss:
                    loss += tf.reduce_sum(model.losses)
                # ---

            # 勾配をNNに反映するおまじないコード
            grads = tape.gradient(loss, model.trainable_variables)
            optimizer.apply_gradients(zip(grads, model.trainable_variables))

            # 1train loss
            epoch_loss_list.append(loss.numpy())

            # 1train metric
            y_pred = model(x)
            metric.update_state(y_true, y_pred)
            
            # STEPS_PER_EPOCH 回数だけ繰り返す
            if step >= STEPS_PER_EPOCH:
                break

        loss_list.append(np.mean(epoch_loss_list))
        acc_list.append(metric.result().numpy())

        # --- 1 epoch validation
        epoch_val_loss_list = []
        metric.reset_state()
        for x, y_true in validate_ds:
            y_pred = model(x)
            val_loss = loss_func(y_true, y_pred)
            if add_normalize_loss:
                val_loss += tf.reduce_sum(model.losses)
            epoch_val_loss_list.append(val_loss.numpy())
            metric.update_state(y_true, y_pred)
        
        val_loss_list.append(np.mean(epoch_val_loss_list))
        val_acc_list.append(metric.result().numpy())

    # --- グラフ出力
    plt.figure(figsize = (4, 3))
    plt.plot(loss_list, label="loss")
    plt.plot(val_loss_list, label="val_loss")
    plt.ylim([0, 1])
    plt.grid()
    plt.legend()
    plt.xlabel('Epoch')
    plt.show()

    plt.figure(figsize = (4, 3))
    plt.plot(acc_list, label="acc")
    plt.plot(val_acc_list, label="val_acc")
    plt.ylim([0, 1])
    plt.grid()
    plt.legend()
    plt.xlabel('Epoch')
    plt.show()

(1)正則化項がないモデル

チュートリアルと同じモデルで試してみます。

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(512, activation='elu'),
    kl.Dense(1),
])
fit(model, add_normalize_loss=False)

output5.png
output6.png

チュートリアルと同じ結果ですね。

(2)正則化項があり、lossに正則化項の損失を加味しないモデル

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(1)
])
fit(model, add_normalize_loss=False)

output7.png
output8.png

(1)とほぼ同じですね。
正則化項は反映されてなさそう…。

(3)正則化項があり、lossに正則化項の損失を加味するモデル

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dense(1)
])
fit(model, add_normalize_loss=True)

output9.png
output10.png

lossと正解率(acc)がほぼ同じになりました。
正則化項がしっかり反映されています。

おまけ、dropout層を追加

lossは改善されましたが肝心の正解率(acc)があまり変わらなかったのでdropout層も追加してみました。

model = tf.keras.Sequential([
    kl.Input(shape=(FEATURES,)),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dropout(0.5),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dropout(0.5),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dropout(0.5),
    kl.Dense(512, activation='elu', kernel_regularizer=keras.regularizers.l2(0.001)),
    kl.Dropout(0.5),
    kl.Dense(1)
])
fit(model, add_normalize_loss=True)

output11.png
output12.png

lossはより安定してますが、accは下がったような？

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1