天球を描いてアニメーションを作ることで、望遠鏡の経緯台式架台や視差角の概念を理解する

はじめに

この前の記事で https://qiita.com/phyblas/items/52dc1bd113aff3745a8d
直接撮像法による系外惑星の探索について説明しました。

その中で『視差角』と『経緯台式架台』について言及しましたが、あまり詳しく説明していません。
言葉で説明しても難しいことだと思うので、補充として、今回はそれについて、pythonで絵を描いてアニメーションで解説します。

実装に使うモジュール

この記事の実装で以下のpythonモジュールを使います

• numpy
• matplotlib
• astropy
• imageio

astropyは主に座標変換に使います。

astropyの座標変換機能についてはこの前の記事でもよく使っていました。
https://qiita.com/phyblas/items/a801b0f319742245ad2e
https://qiita.com/phyblas/items/9a087ad1f73aca5dcbe5
https://qiita.com/phyblas/items/0d7623dbaf6866fb5bbd

matplotlibによって描かれた画像をgifアニメーションにするためにimageioを使います

地平座標と赤道座標

地平座標（equatorial coordinate）はある特定の場所から空を見る時に天体の位置を示す座標で、方位角と仰俯角で天体の位置を特定するものです。

それに対し、赤道座標（horizontal coordinate）は赤経と赤緯で天体の位置を示す座標です。

天体の位置は天の赤道座標に固定されているが、観測する人間や望遠鏡は地平座標に固定されているものです。

地球は常に回っているため、赤道座標が回っているように見えて、空を見上げたら天体は時間によって移動していくように見えます。

回転軸は赤道座標の北極と南極にあるため、空における全ての天体は赤経値の線に沿って移動するものです。

その天体の移動をmatplotlibで描いてimageioで動くgifにします。

座標変換はastropyに任せます。時間と場所を指定したらすぐ変換できるのでとても便利です。そうしたら赤道座標のグリッドと観測したい天体の位置も地平座標に表示できます。

まずは観測する時間と場所と天体を決めなければならないので、ここでは

• 時間は、この記事を書いた2019年9月15日の夜
• 場所は、経度133°35′48.3″、緯度34°34′36.5″にある岡山天体物理観測所のせいめい望遠鏡
• 天体は、赤経22h57m39.04625s、赤緯-29°37′20.0533″にあるフォマルハウト

にします。

ちなみにフォマルハウトを選ぶ理由はちょうど赤緯-30°くらいにあるし、ちょうど今この時期では夜の間に空を昇るし、それにこの星は初めて直接撮像法で系外惑星も発見された星なのです。

実装

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import astropy.units as u
from astropy.coordinates import SkyCoord,EarthLocation,AltAz,Angle
from astropy.time import Time
import imageio

koko_keido = Angle('133° 35′ 48.3″') # 観測値の経度
koko_ido = Angle('34° 34′ 36.5″') # 観測値の緯度
# 観測の位置を決めるオブジェクト
koko = EarthLocation(lat=koko_ido,lon=koko_keido)
# 観測時間、日本の20時に始まるが、๊UTCにする必要があるので9時間でひく
toki = Time('2019-09-15 20:00:00') - 9*u.hour + np.arange(0,8,0.5)*u.hour

# 地平座標のグリッド
az,alt = np.meshgrid(np.arange(0,360.1,3),np.arange(0,90.1,3))
chihei_grid = SkyCoord(az=az,alt=alt,unit='deg',frame='altaz').cartesian.xyz

# 赤道座標のグリッド
ra,dec = np.meshgrid(np.arange(0,360.1,1),np.arange(-90,90.1,15))
sekidou_grid = SkyCoord(ra=ra,dec=dec,unit='deg')

# 観測したい天体の赤道による位置
hoshi_sekkei = Angle('22h 57m 39.04625s') # 赤経
hoshi_sekii = Angle('-29° 37′ 20.0533″') # 赤緯
hoshi_sekidou = SkyCoord(ra=hoshi_sekkei,dec=hoshi_sekii)

gif = [] # 絵のフレームを納めるリスト
# フレーム毎に繰り返し絵を描く
for ima in toki:
    # その時間のその場所の地平座標を示すオブジェクト
    kokoima = AltAz(obstime=ima,location=koko)

    fig = plt.figure(figsize=[6,6],dpi=80)
    # 地平座標のグリッドを描く
    ax = plt.axes([0,0,1,1],projection='3d',xlim=[-0.6,0.6],ylim=[-0.6,0.6],zlim=[-0.4,1],facecolor='k')
    ax.plot_wireframe(*chihei_grid,rstride=10,cstride=10,color='#dddddd',alpha=0.4)

    # 地平座標で赤道座標のグリッドを描く
    sekidou_grid_xyz = sekidou_grid.transform_to(kokoima).cartesian.xyz
    sekidou_grid_xyz[:,sekidou_grid_xyz[2]<0] = np.nan # 地面より低いところを除外
    ax.plot_wireframe(*sekidou_grid_xyz,cstride=30,color='#ff7777',linestyle='--',alpha=0.6)

    # 地平座標における天体の位置
    hoshi_chihei = hoshi_sekidou.transform_to(kokoima)
    # 直交座標に変換する
    hoshi_xyz = hoshi_chihei.cartesian.xyz
    # 地平座標で天体の位置をマーク
    ax.scatter(*hoshi_xyz,s=250,marker='*',color='#9999ff')
    # 望遠鏡から天体までの線
    ax.plot(*np.stack([(0,0,0),hoshi_xyz],1),color='#99bbff',ls='--')
    # 望遠鏡を描く
    ax.plot(*np.stack([(0,0,0),hoshi_xyz],1)*0.2,color='#99bbff',lw=10)
    # 望遠鏡から天頂までの線
    ax.plot([0,0],[0,0],[0,1],color='#ffffdd',alpha=0.6)

    plt.axis('off')
    # 時間と方位角と仰俯角を書く
    az = hoshi_chihei.az.to_string(unit=u.degree, sep=['° ','′ ','″'])
    alt = hoshi_chihei.alt.to_string(unit=u.degree, sep=['° ','′ ','″'])
    ax.text(0,0,1.2,f'{(ima+9*u.hour).datetime}\naz = {az}\nalt = {alt}',color='#ccffcc',size=18,ha='center')
    ax.view_init(30,105)
    fig.canvas.draw()
    gif.append(np.array(fig.canvas.renderer._renderer))
    plt.close()

# .gifファイル保存
imageio.mimsave('fomalhaut_20190915.gif',gif,fps=4)

結果

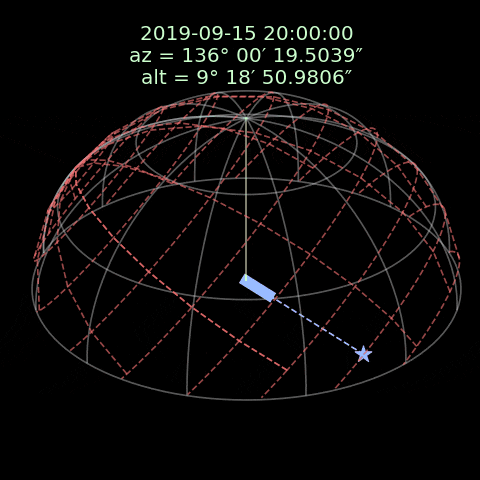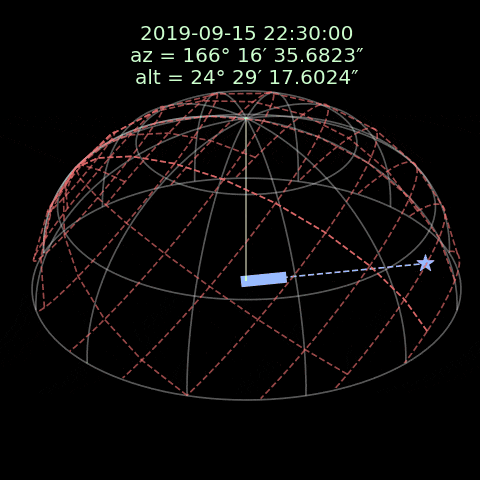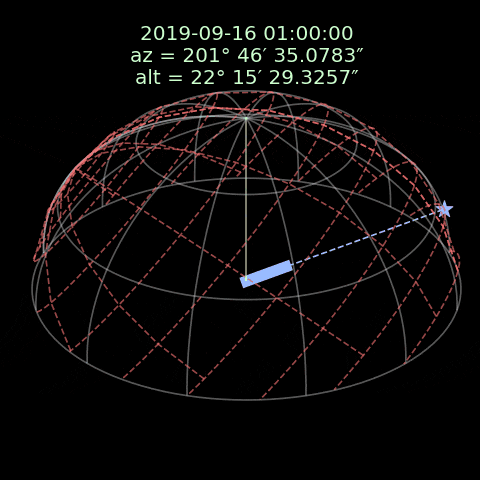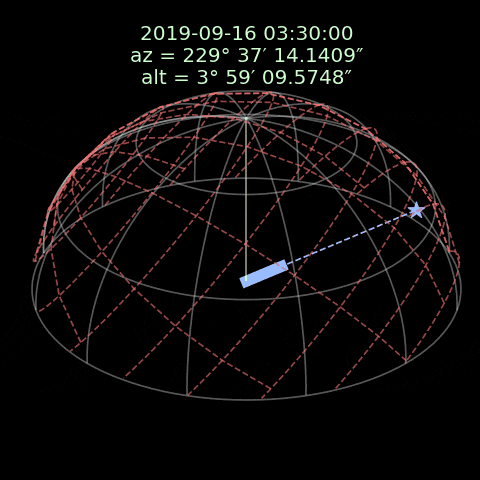
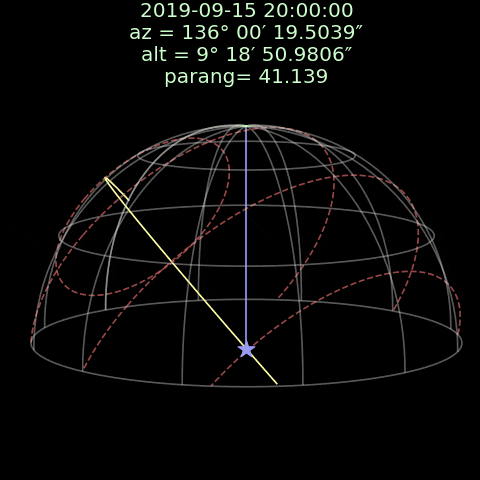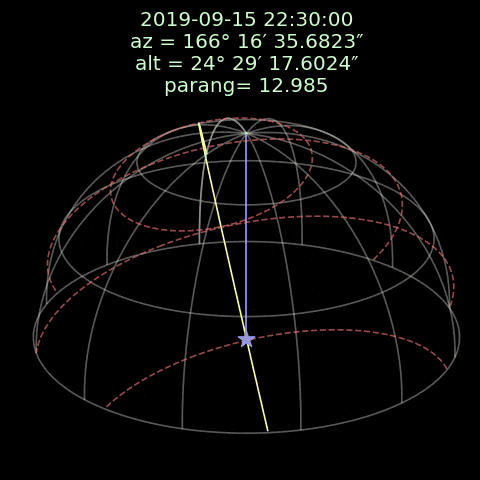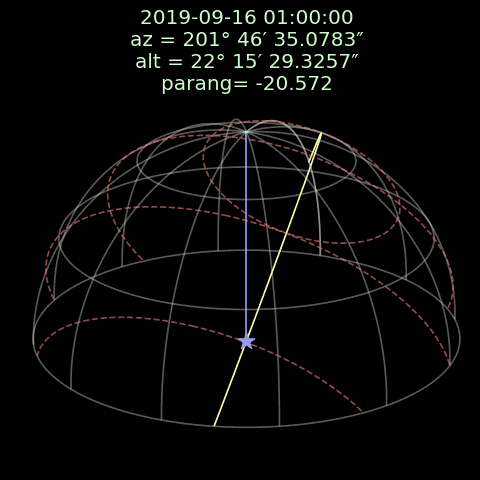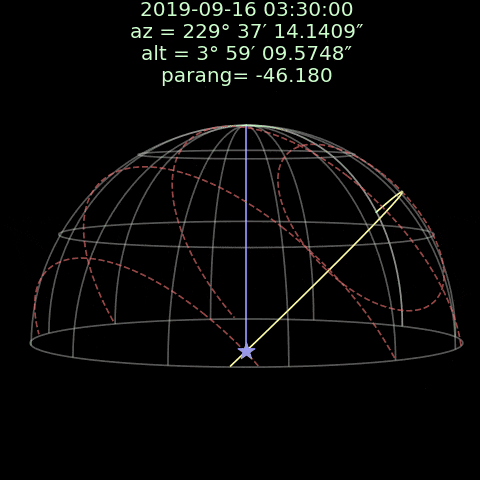
この画像では、白い線は地平座標で、赤い線は赤道座標です。フォマルハウトは赤道座標と一緒に移動していて地平座標における位置は時間によって変わります。

経緯台式架台の望遠鏡による観測

望遠鏡は回転に使う座標によって二種類分けられます。

• 回転軸が水平軸であるのは経緯台式架台
• 回転軸が赤経軸であるのは赤道儀式架台

赤道儀を使ったら回転軸は天体と同じ、赤道座標なので、天体を追う時はただ向かう方向を変えるだけで制御しやすいが、経緯台式架台の方が作りやすいため、すばる望遠鏡やせいめい望遠鏡など大型望遠鏡が大体は経緯台を使用しています。

天体は赤経値の線に沿って移動している時には方位角も仰俯角も変わっていきます。その上で、経緯台を使う望遠鏡の視野に入る天体の見かけの角度は変わっていきます。

その差分の角度は視差角（parallactic angle）と呼びます。

視差角はこの公式で計算できます。

parang = \arcsin \left(\frac{\sin(az)\cos(lat)}{\cos(dec)}\right)

その視差角の変化をわかりやすくするためにアニメーションで解説します。

実装

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import astropy.units as u
from astropy.coordinates import SkyCoord,EarthLocation,AltAz
from astropy.coordinates import Angle
from astropy.time import Time
import imageio

koko_keido = Angle('133° 35′ 48.3″')
koko_ido = Angle('34° 34′ 36.5″')
koko = EarthLocation(lat=koko_ido,lon=koko_keido)
toki = Time('2019-09-15 20:00:00')-9*u.hour + np.arange(0,8,0.5)*u.hour

az,alt = np.meshgrid(np.arange(0,360.1,3),np.arange(0,90.1,3))
chihei_grid = SkyCoord(az=az,alt=alt,unit='deg',frame='altaz').cartesian.xyz

ra,dec = np.meshgrid(np.arange(0,360.1,1),np.arange(-90,90.1,30))
sekidou_grid = SkyCoord(ra=ra,dec=dec,unit='deg')

hoshi_sekkei = Angle('22h 57m 39.04625s')
hoshi_sekii = Angle('-29° 37′ 20.0533″')
hoshi_sekidou = SkyCoord(ra=hoshi_sekkei,dec=hoshi_sekii)

lis_parang = [] # 視差角を納めるリスト
gif = []
for ima in toki:
    kokoima = AltAz(obstime=ima,location=koko)

    fig = plt.figure(figsize=[6,6],dpi=80)
    ax = plt.axes([0,0,1,1],projection='3d',xlim=[-0.6,0.6],ylim=[-0.6,0.6],zlim=[-0.1,1.1],facecolor='k')
    ax.plot_wireframe(*chihei_grid,rstride=10,cstride=10,color='#dddddd',alpha=0.4)

    sekidou_grid_xyz = sekidou_grid.transform_to(kokoima).cartesian.xyz
    sekidou_grid_xyz[:,sekidou_grid_xyz[2]<0] = np.nan
    ax.plot_wireframe(*sekidou_grid_xyz,cstride=None,color='#ff7777',linestyle='--',alpha=0.6)

    hoshi_chihei = hoshi_sekidou.transform_to(kokoima)
    hoshi_xyz = hoshi_chihei.cartesian.xyz
    ax.scatter(*hoshi_xyz,s=250,marker='*',color='#9999ff')

    # 赤道座標の北極から天体を経過して南極まで曲線
    kyoku_chihei = SkyCoord(ra=hoshi_sekkei,dec=np.arange(-90,90.1,1),unit=('hourangle','deg')).transform_to(kokoima)
    kyoku_xyz = kyoku_chihei.cartesian.xyz
    kyoku_xyz[2][kyoku_xyz[2]<0] = np.nan
    ax.plot(*kyoku_xyz,color='#ffff99')
    ax.view_init(hoshi_chihei.alt.value,hoshi_chihei.az.value)

    # 天頂から天体までの曲線
    tenchou_chihei = SkyCoord(az=hoshi_chihei.az,alt=np.linspace(hoshi_chihei.alt.value,90,101),unit='deg',frame='altaz')
    tenchou_xyz = tenchou_chihei.cartesian.xyz
    ax.plot(*tenchou_xyz,color='#9999ff')

    # 時間と方位角と仰俯角と視差角を書く
    az = hoshi_chihei.az.to_string(unit=u.degree, sep=['° ','′ ','″'])
    alt = hoshi_chihei.alt.to_string(unit=u.degree, sep=['° ','′ ','″'])
    parang = np.degrees(np.arcsin(np.sin(hoshi_chihei.az.radian)*np.cos(koko.lat.radian)/np.cos(hoshi_sekidou.dec.radian)))
    ax.text(0,0,1.2,f'{(ima+9*u.hour).datetime}\naz = {az}\nalt = {alt}\nparang= {parang:.3f}',color='#ccffcc',size=18,ha='center')

    plt.axis('off')
    fig.canvas.draw()
    gif.append(np.array(fig.canvas.renderer._renderer))
    plt.close()
    lis_parang.append(parang)

# 図1を保存
imageio.mimsave('fomalhaut_20190915_parang.gif',gif,fps=4)

# 図2を描く
plt.figure(figsize=[7,8],dpi=60)
for i,(parang,ima) in enumerate(zip(lis_parang,toki)):
    plt.subplot(4,4,1+i,xlim=[-1,1],ylim=[-1,1],xticks=[],yticks=[],facecolor='k')
    plt.plot([0,0],[0,1],color='#9999ff')
    plt.text(0,0,'$\Delta$',color='#ffff99',size=70,ha='center',va='center',rotation=-parang)
    plt.title(f'{(ima+9*u.hour).datetime:%H:%M}',size=18)
    plt.xlabel('%.1f°'%parang,size=18)
plt.tight_layout()
plt.savefig('fomalhaut_20190915_parang1.png')
plt.close()

# 図3を描く
plt.figure(figsize=[7,8],dpi=60)
for i,(parang,ima) in enumerate(zip(lis_parang,toki)):
    plt.subplot(4,4,1+i,xlim=[-1,1],ylim=[-1,1],xticks=[],yticks=[],facecolor='k')
    plt.plot([0,-np.tan(np.radians(parang))],[0,1],color='#9999ff')
    plt.text(0,0,'$\Delta$',color='#ffff99',size=70,ha='center',va='center')
    plt.title(f'{(ima+9*u.hour).datetime:%H:%M}',size=18)
    plt.xlabel('%.1f°'%parang,size=18)
plt.tight_layout()
plt.savefig('fomalhaut_20190915_parang2.png')
plt.close()

実行したら3枚画像ができます

図1：黄色の線は天体を通して赤道座標の北極から南極までの大円上の曲線で、紫色の線は天頂から天体までの大円上の曲線です。

その黄色と紫色の線によって成す角度は視差角です

図2：時間によって変化していく視差角を使って回っているΔを表示したのです。地平座標における観測者から見る天体の角度はこうやって回っていきます。だから経緯台で観測する時は視差角によって視野を逆に回す場合が多いです。

図3：視野を回したら、天体の角度は固定されます。

（注意：コードや絵はここまで、以下は天文学の説明ばかり）

視野を回すべきかどうかの話

経緯台を使う望遠鏡でを天体の写真を撮る時には視差角によって視野を回転をするのが一般的ですが、そうしない場合もあります。

望遠鏡で天体を観測する時は色んなノイズが起こります。その中で、PSFやスペックルノイズなど光学系に由来する準静的なノイズであり、視野に固定されるノイズがあります。

視野を回して撮影すると、このようなノイズも天体と共に視野と一緒に移動するので、ノイズから天体の写真から分解することが難しくなります。

ノイズと天体を分解する必要がある場合視野を回転しない方が寧ろいい結果になります。

ただし、視野を回転せずに長時間露出で撮影すると天体の姿がぼけて写るためよくないのです。この場合、短時間露出で何枚もの写真を撮って後で回して合成する必要があります。

角度差分撮像（ADI）方法の概念

視野を回転せずに、色んな写真を撮影したら、それらの写真の中のノイズが同じような形だが、天体だけは回っていきます。

全ての写真を分析するととノイズのパターンがわかり、そのノイズを全ての写真からひくことで、ノイズを消すことができます。

後は写真を回転して各枚の写真の中の天体の位置を一致して写真を合わせたら、天体がはっきり写る一枚の写真ができます。

こういう方法は角度差分撮像（angular differential imaging、ADI）と呼びます。

恒星の周りにある系外惑星を探す時には、恒星からの僅かなノイズでも惑星の光よりも強いため、惑星をはっきり見えるためにはノイズを消すことが重要なことになって、この方法で撮影することが一般的です。

参考資料

• http://www.asj.or.jp/geppou/archive_open/2012_105_03/105_148.pdf
• https://astroexercise.wiki.fc2.com/wiki/天体の位置
• http://www.kusastro.kyoto-u.ac.jp/~iwamuro/LECTURE/GENERAL2/index.html
• http://asait.world.coocan.jp/kuiper_belt/eclipse/chinese_astronomy.htm