Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

astropyAdvent Calendar 2019

Day 4
@phyblas(雛星 φυβλας)

astropyとmatplotlibで天球上の太陽の軌道を描いてアナレンマを作ってみたり、日時計について説明してみたり、アニメーションを作成してみたり

Posted at

この前の記事ではastropyのget_sunという関数を使って太陽の位置の変化について説明しました。https://qiita.com/phyblas/items/9a087ad1f73aca5dcbe5

今回はその続きとして、アナレンマというものについて説明しながらその形をastropyとmatplotlibで描きます。

アナレンマとは

地球の公転軌道は楕円である同時に、自転軸も偏っているため、毎日の同じ時間で太陽を観測したら、太陽は天球の同じ場所にあるのではなく毎日変わるんです。

偏っている自転軸は毎日の同じ時間の太陽高さを左右し、楕円の公転軌道は方位角を左右するので、一年間の毎日の同じ時間の太陽の位置を記録してプロットみたら、「8」という字のような形に見えてそれはけ「アナレンマ」と呼ばれます。

ちなみにこんな姿になるのは地球の場合で、傾斜角と離心率の組み合わせる関係次第では、火星など他の惑星では滴の形になることもあります。

アナレンマについてもっと詳しい原理の説明はこの記事 http://koyomi8.com/reki_doc/doc_0553.htm

それと、太陽のアナレンマを計算する方法を説明してrubyで実装した@HMMNRSTさんの記事 https://qiita.com/HMMNRST/items/ec0c3a9e8e5deeac8aa6

この記事を書きたいと思ったは@HMMNRSTさんのこの記事を読んだのはきっかけです。

これを読んだらアナレンマを描く方法はわかるようになりますが、方程式いっぱいで難しいですね。でもastropyのget_sunを使って太陽の位置を持てめたら簡単に作れます。

そんな方法を思いついたのは、astropyを使って日の出の時間を求める方法を説明した@nankiさんの記事を読んだのはきっかけです。 https://qiita.com/nanki/items/97191fee71ec5a3255f5

真昼のアナレンマを描く

まずは一年間の毎日の12時の太陽の位置を見てみます。前の記事と同じように、観測する芭蕉は東京都三鷹市国立天文台にします。

季節の変化と比べるために春分などの節気の日の表記も付け加えます。

import numpy as np
import matplotlib.pyplot as plt
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun,SkyCoord,EarthLocation,AltAz

koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1') # 観測する場所
sekki = u'立春 春分 立夏 夏至 立秋 秋分 立冬 冬至'.split(' ') # 節気の名前
tsukihi = ['2-4','3-21','5-6','6-22','8-8','9-23','11-8','12-22'] # 節気の月日
t_sekki = [int((astropy.time.Time('2019-%s'%t)-astropy.time.Time('2019-1-1')).value) for t in tsukihi] # 節気1月1日からの日数
toki = astropy.time.Time('2019-1-1 12:00') - koko.lon.value/15*u.hour + np.arange(365)*u.day # 毎日の12時の時間

taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko)) # 太陽の位置を取得
az,alt = taiyou.az.value,taiyou.alt.value # 方位角と仰俯角
plt.gca(aspect=1)
plt.scatter(az,alt,c=np.arange(365),s=1,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.scatter(az[t_sekki],alt[t_sekki],c='w',s=100,marker='*',edgecolor='k')
for t,s in zip(t_sekki,sekki):
    plt.text(az[t],alt[t]+2,s,fontname='AppleGothic',ha='center')
plt.xlabel(u'方位角',fontname='AppleGothic')
plt.ylabel(u'仰俯角',fontname='AppleGothic')
plt.show()

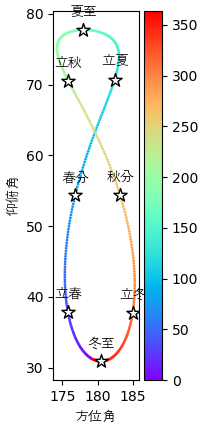
軌道を描いてみたらちゃんとアナレンマの形になっているとかわかります。

真昼の太陽はほぼ方位角180度、つまり南の方にあるので、アナレンマも180度を中心にしています。夏至の日には「$90°+23.5°-緯度$」に一番太陽が高く昇るが、冬至の日には「
$90°-23.5°-緯度$」で一番低いとわかります。春分と秋分の日には太陽が 「
$90°-緯度$」 のところにあります。

ただし、前の記事でも説明したように、緯度が23.5度より低いところでは、夏至の日は太陽の一番高い日ではなく、真昼の太陽は北の方に仰俯角は「$90°-23.5°+緯度$」となります。

注意：これはあくまで北半球の場合です。南半球なら全部逆。

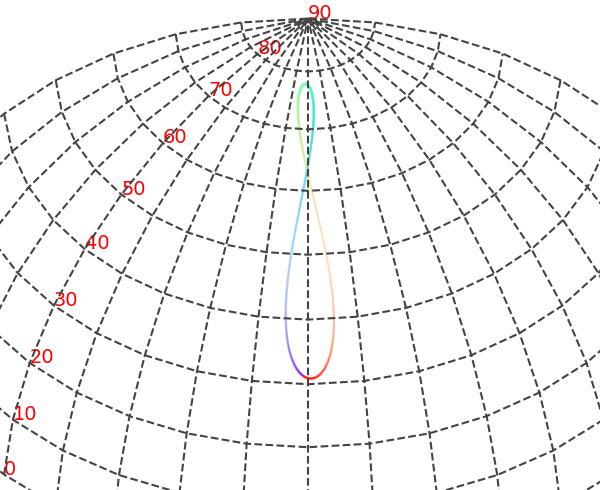
このクラフは球面座標系の角度で示すだけで、本当に見える形とはちょっと違うので、実際に三次元の直交座標に変換して見上げます。

from mpl_toolkits.mplot3d import Axes3D

# 方位角と仰俯角から直交座標のxyzに変換
sx,sy,sz = SkyCoord(az=az,alt=alt,unit='deg',frame='altaz').cartesian.xyz.value
fig = plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[-0.4,0.4],ylim=[-0.4,0.4],zlim=[0,0.8])
ax.invert_yaxis()
ax.scatter(sx,sy,sz,c=np.arange(365),s=1,cmap='rainbow')
aa = np.meshgrid(np.arange(90,271,10),np.arange(0,91,10))
# 方位角と仰俯角のグリッドを描く
gx,gy,gz = SkyCoord(az=aa[0],alt=aa[1],unit='deg',frame='altaz').cartesian.xyz.value
ax.plot_wireframe(gx,gy,gz,color='#444444',linestyle='--')
for i in range(len(gx)):
    ax.text(gx[i,4],gy[i,4],gz[i,4],'%d'%aa[1][i,0],color='r',size=14)
plt.axis('off')
ax.view_init(-45,0)
plt.show()

こうやってアナレンマの姿ができました。

注意：地平座標から変換するとy値は普通の直交座標系とは逆の方向なのでinvert_yaxisを使うのです。

アナレンマの影による日時計

実際によくアナレンマの姿を見かけるのは太陽の影によって時間を表示する日時計です。

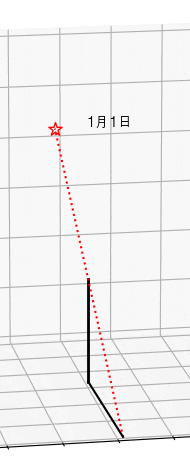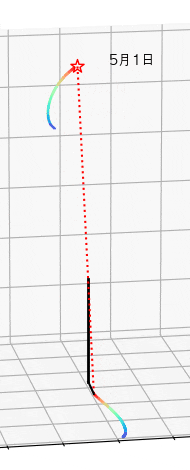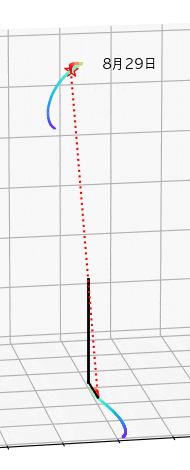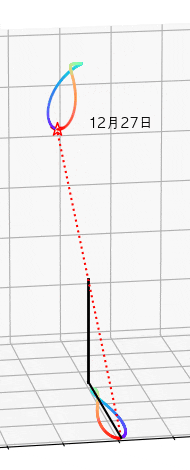
一番簡単な日時計は柱一本で成ります。もし毎日の真昼の時の柱の影の尖端の位置を描いたら地面でアナレンマの形ができます。直接太陽を観測するよりも柱の影を見る方が簡単です。

言葉では説明しにくいのでアニメーションを作って説明します。

アニメーションを作るのは以下のコード。柱の高さは1メートルにします。

import numpy as np
import matplotlib.pyplot as plt
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun,SkyCoord,EarthLocation,AltAz
from mpl_toolkits.mplot3d import Axes3D
import imageio

koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1')
toki = astropy.time.Time('2019-1-1 12:00') - koko.lon.value/15*u.hour + np.arange(365)*u.day
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
az,alt = taiyou.az.value,taiyou.alt.value
x = -np.cos(np.radians(az))/np.tan(np.radians(alt))
y = -np.sin(np.radians(az))/np.tan(np.radians(alt))
sx,sy,sz = SkyCoord(ra=az,dec=alt,unit='deg').cartesian.xyz.value*2
sz += 1

gif = []
for i in range(73):
    t = i*5
    fig = plt.figure(figsize=[6,6])
    ax = plt.axes([0,0,1,1],projection='3d',xlim=[-1.5,1.5],ylim=[-1.5,1.5],zlim=[0,3])
    ax.invert_yaxis()
    ax.scatter(sx[:t],sy[:t],sz[:t],c=np.arange(t),s=1,cmap='rainbow')
    ax.scatter(sx[t],sy[t],sz[t],c='w',s=100,marker='*',edgecolor='r')
    ax.text(sx[t],sy[t]-0.3,sz[t],u'%s月%s日'%(toki[t].datetime.month,toki[t].datetime.day),fontname='AppleGothic')
    ax.scatter(x[:t],y[:t],0,c=np.arange(t),s=1,cmap='rainbow')
    plt.plot([0,0],[0,0],[0,1],'k',lw=2)
    ax.plot([x[t],sx[t]],[y[t],sy[t]],[0,sz[t]],'r:')
    ax.plot([x[t],0],[y[t],0],[0,0],'k')
    ax.view_init(15,-10)
    ax.set_yticklabels(['' for _ in ax.get_yticks()])
    fig.canvas.draw()
    gif.append(np.array(fig.canvas.renderer._renderer)[65:-65,220:-190])
    plt.close()
imageio.mimsave('analemma.gif',gif,fps=24)

analemma.gif

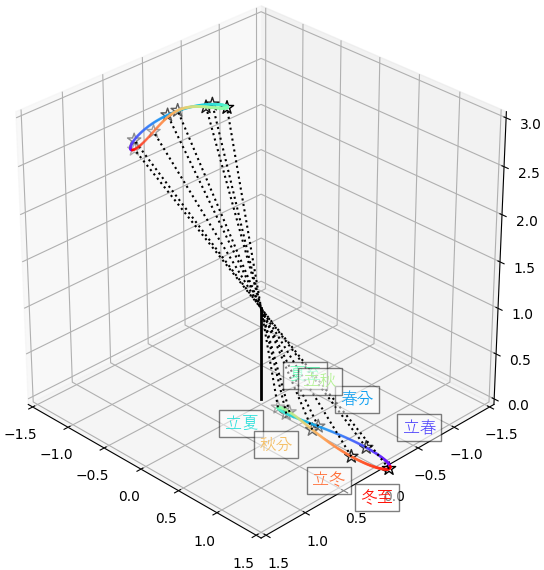
ようするに描くと

sekki = u'立春 春分 立夏 夏至 立秋 秋分 立冬 冬至'.split(' ')
tsukihi = ['2-4','3-21','5-6','6-22','8-8','9-23','11-8','12-22']
t_sekki = [int((astropy.time.Time('2019-%s'%t)-astropy.time.Time('2019-1-1')).value) for t in tsukihi]
koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1')
toki = astropy.time.Time('2019-1-1 12:00') - koko.lon.value/15*u.hour + np.arange(365)*u.day
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
sx,sy,sz = SkyCoord(ra=taiyou.az.value,dec=taiyou.alt.value,unit='deg').cartesian.xyz.value*2
sz += 1
x = -np.cos(np.radians(taiyou.az.value))/np.tan(np.radians(taiyou.alt.value))
y = -np.sin(np.radians(taiyou.az.value))/np.tan(np.radians(taiyou.alt.value))

fig = plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[-1.5,1.5],ylim=[-1.5,1.5],zlim=[0,3])
ax.invert_yaxis()
ax.scatter(sx,sy,sz,c=np.arange(365),s=1,cmap='rainbow')
ax.scatter(x,y,0,c=np.arange(365),s=1,cmap='rainbow')
ax.plot([0,0],[0,0],[0,1],'k',lw=2)
ax.scatter(x[t_sekki],y[t_sekki],0,c='w',s=100,marker='*',edgecolor='k')
ax.scatter(sx[t_sekki],sy[t_sekki],sz[t_sekki],c='w',s=100,marker='*',edgecolor='k')
b = {'fc':'w','lw':1,'alpha':0.5}
for t,s in zip(t_sekki,sekki):
    ax.plot([x[t],sx[t]],[y[t],sy[t]],[0,sz[t]],'k:')
    c = plt.get_cmap('rainbow')(np.arange(365)[t]/364.)
    ax.text(x[t]*1.3,y[t]+((y[t]>0)-0.3),0.2,s,fontname='AppleGothic',ha='center',size=12,color=c,bbox=b)
ax.view_init(30,-45)
plt.show()

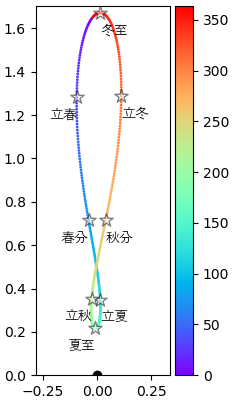
そして地面にある影の軌道だけ描きます。

x = -np.sin(np.radians(taiyou.az.value))/np.tan(np.radians(taiyou.alt.value))
y = -np.cos(np.radians(taiyou.az.value))/np.tan(np.radians(taiyou.alt.value))
plt.gca(aspect=1,xlim=[x.min()*3,x.max()*3],ylim=[0,y.max()*1.02])
plt.scatter(x,y,c=np.arange(365),s=1,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.scatter(x[t_sekki],y[t_sekki],c='w',s=100,marker='*',edgecolor='k',alpha=0.5)
plt.scatter(0,0,c='k')
for t,s in zip(t_sekki,sekki):
    plt.text(x[t],y[t]-0.1,s,fontname='AppleGothic',ha=['left','right'][x[t]<0])
plt.show()

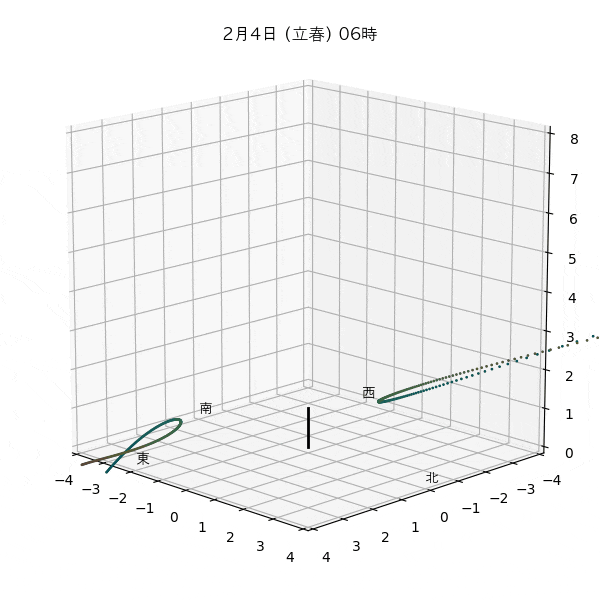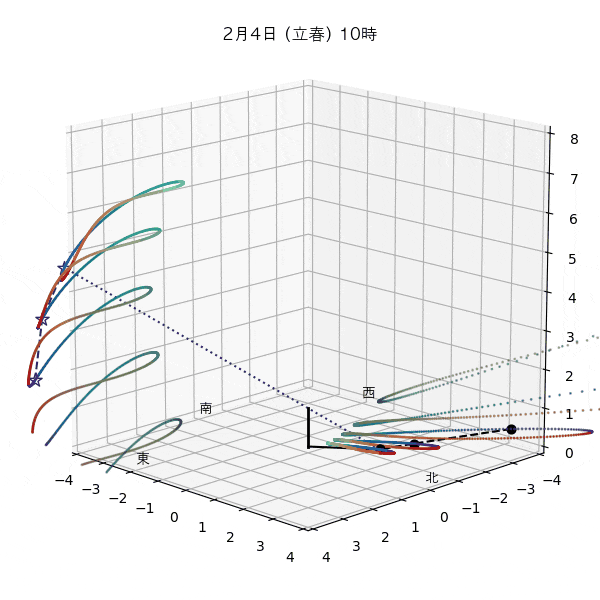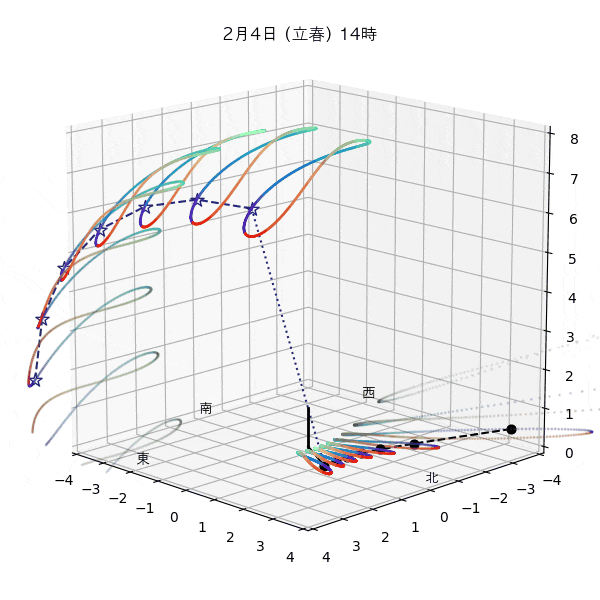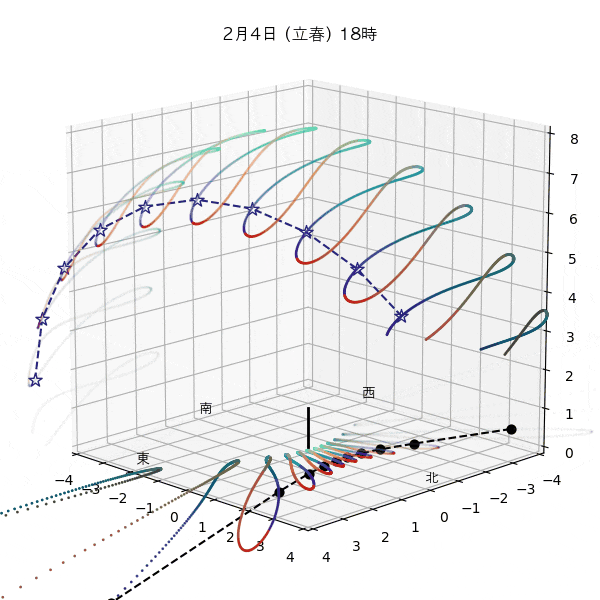
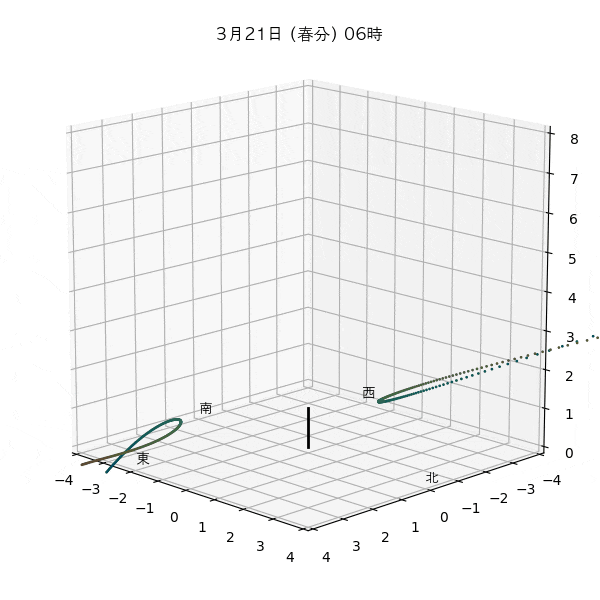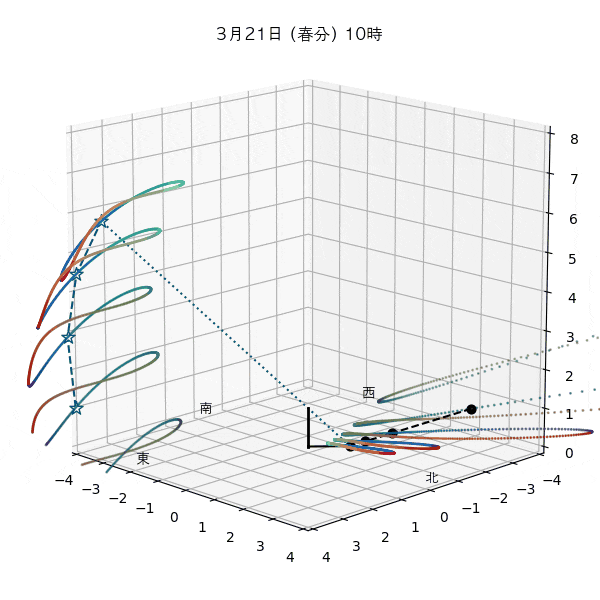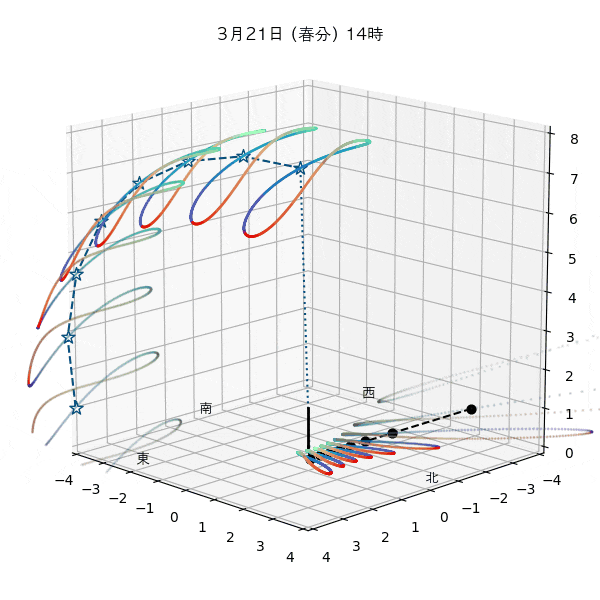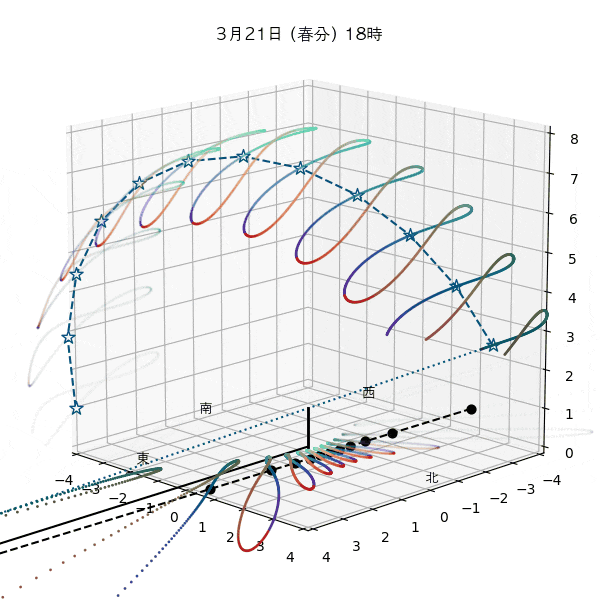
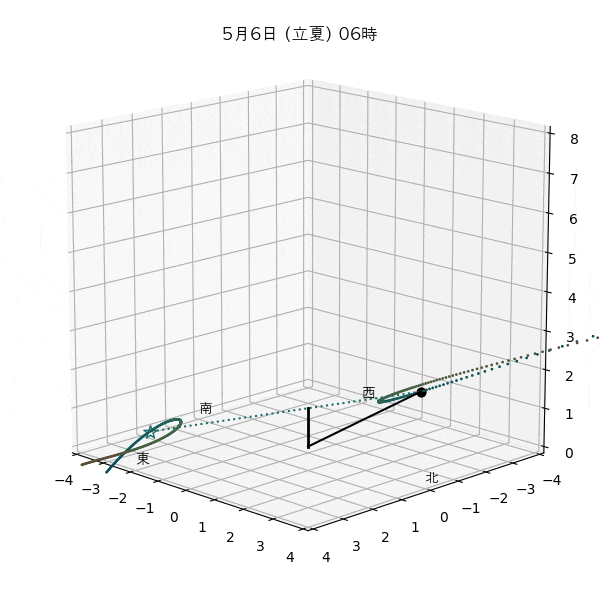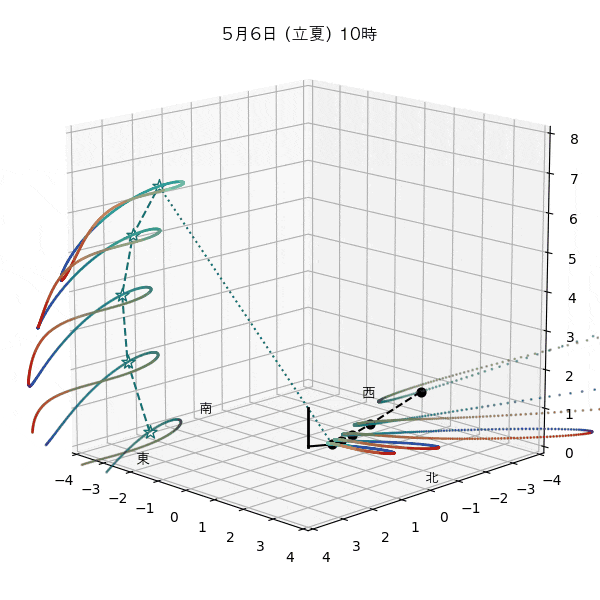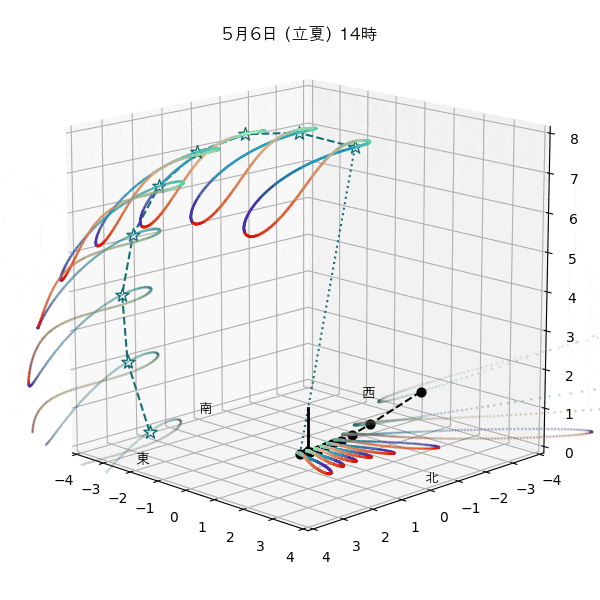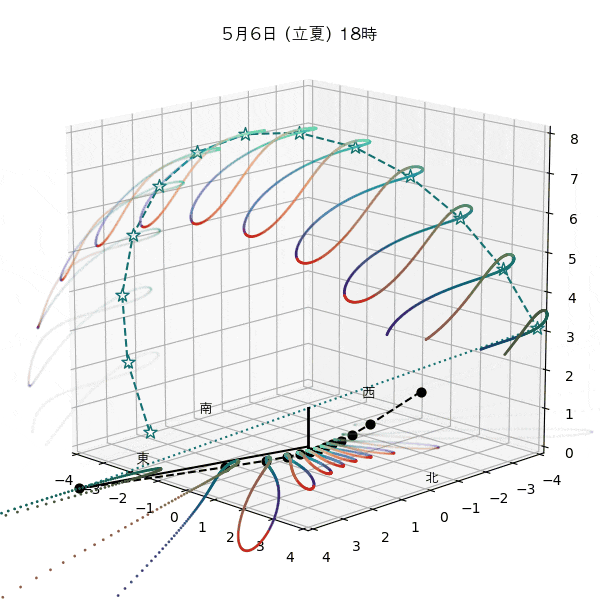
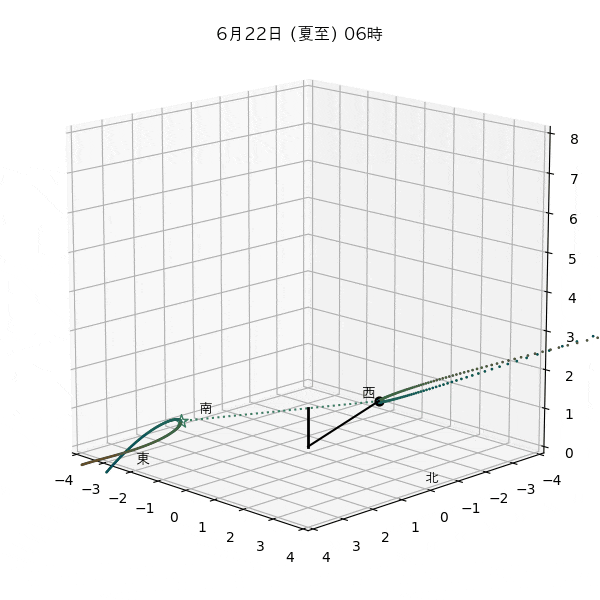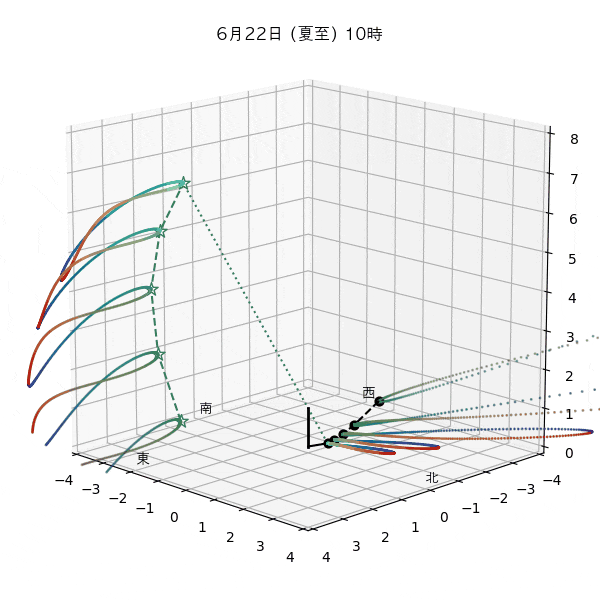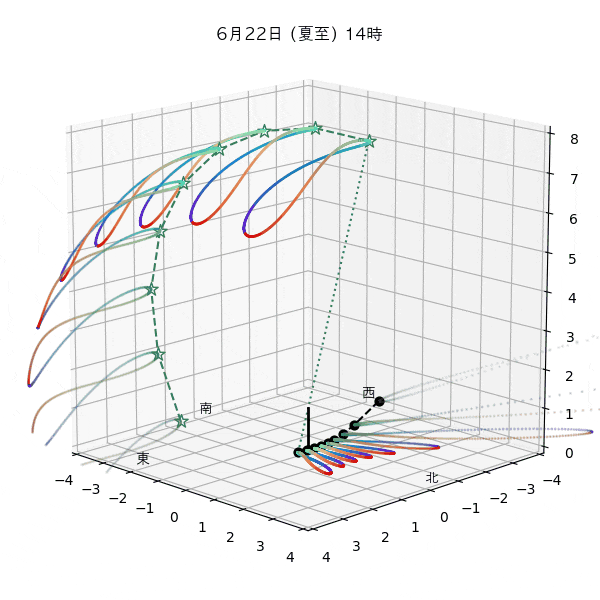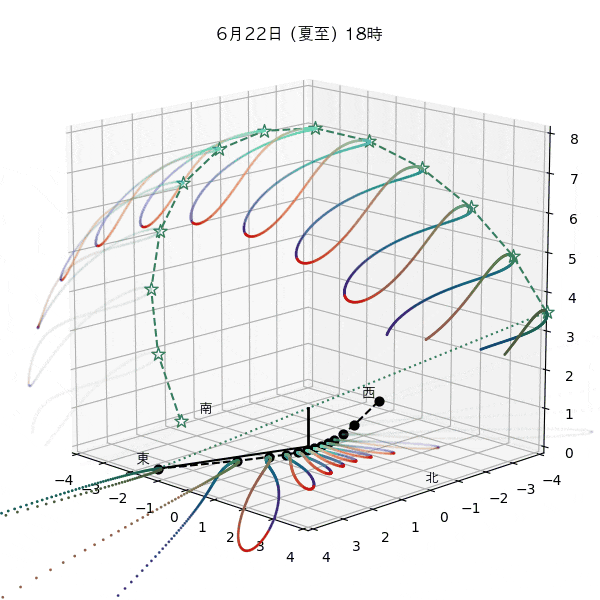
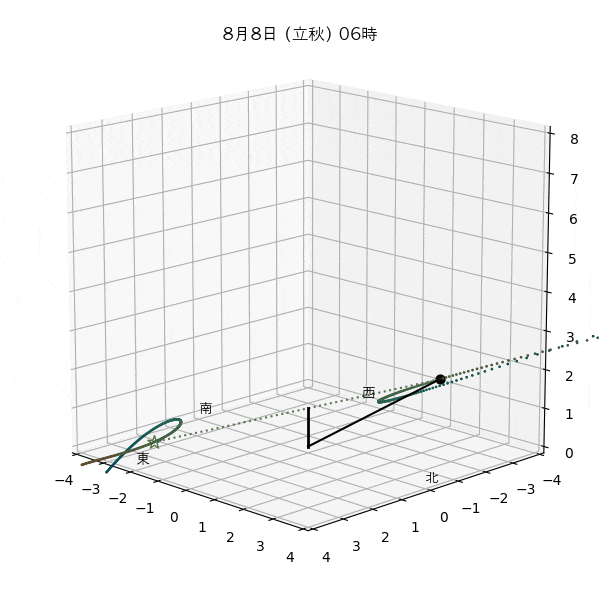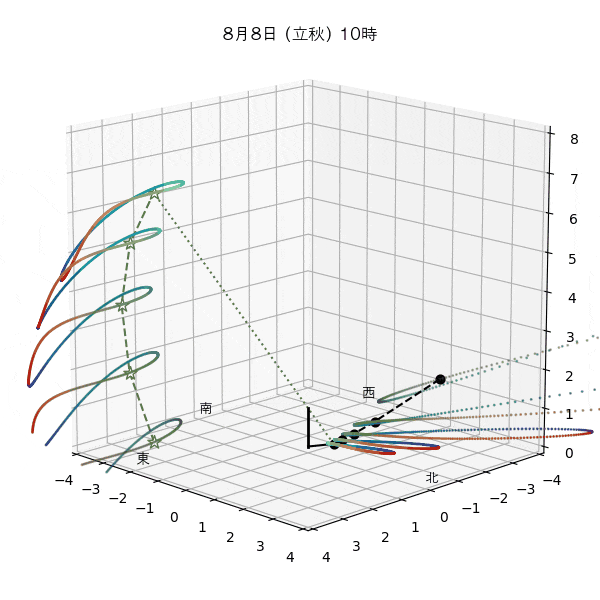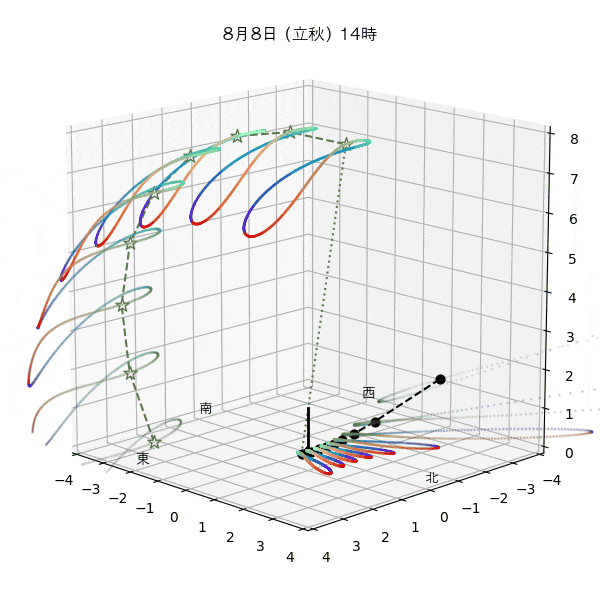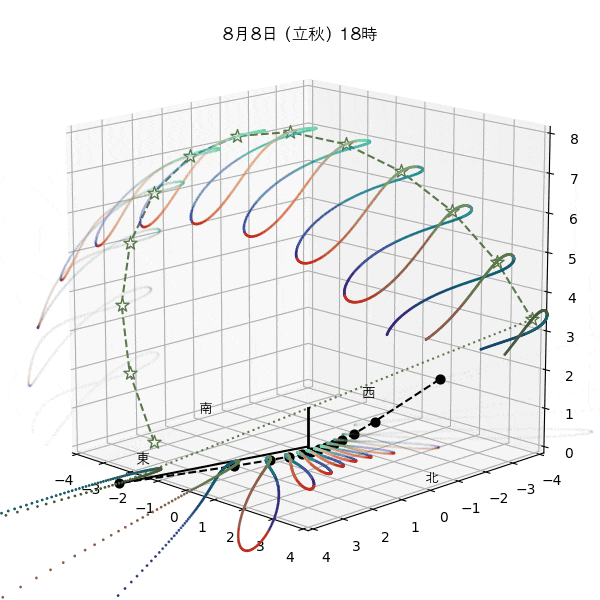
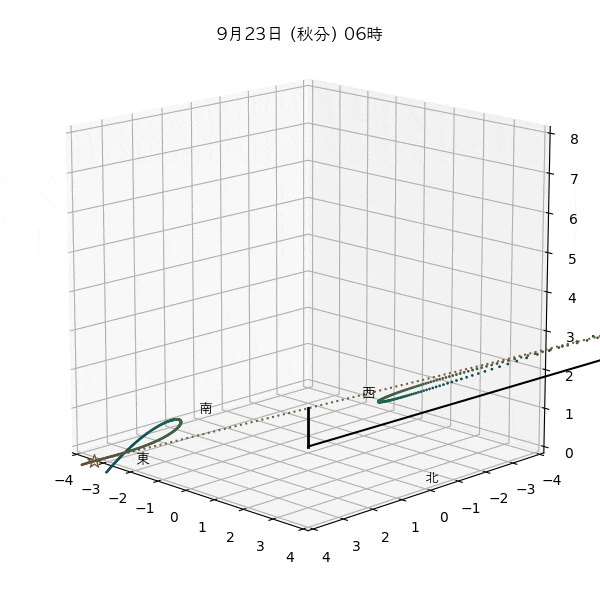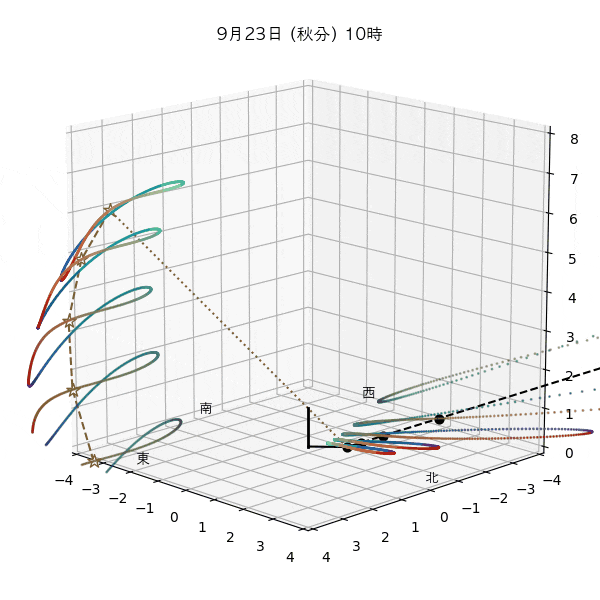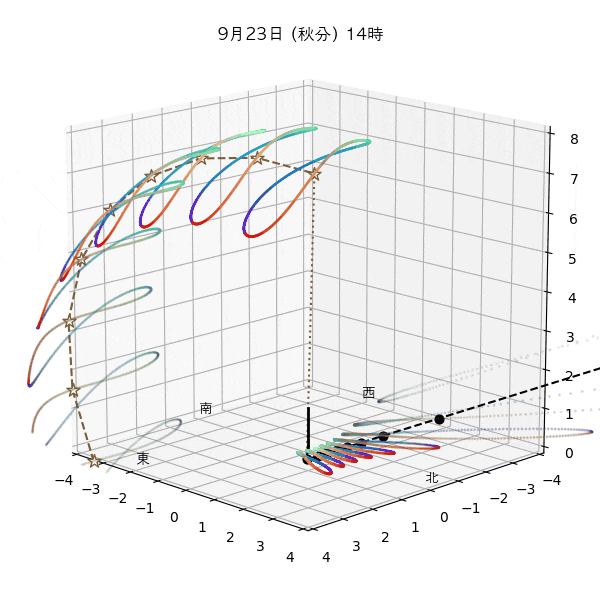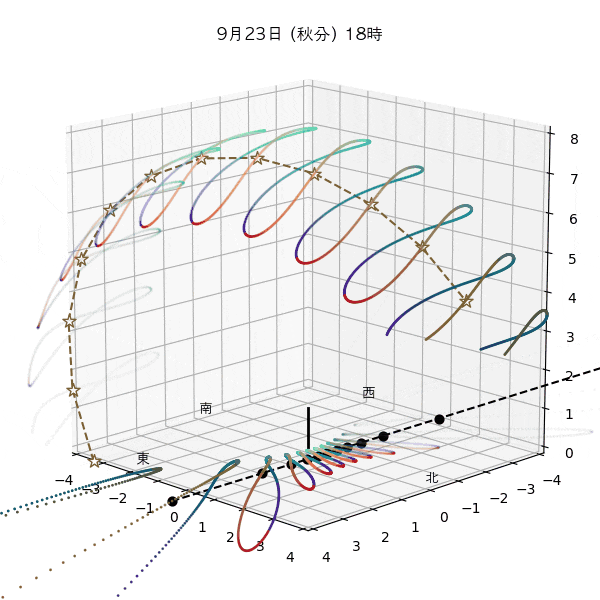
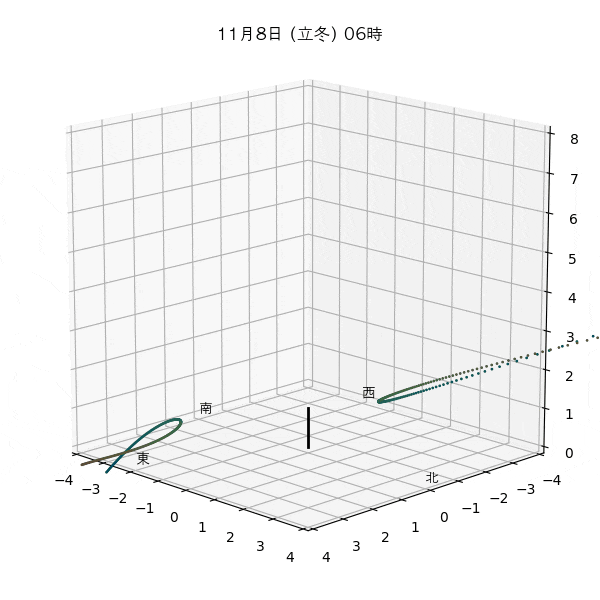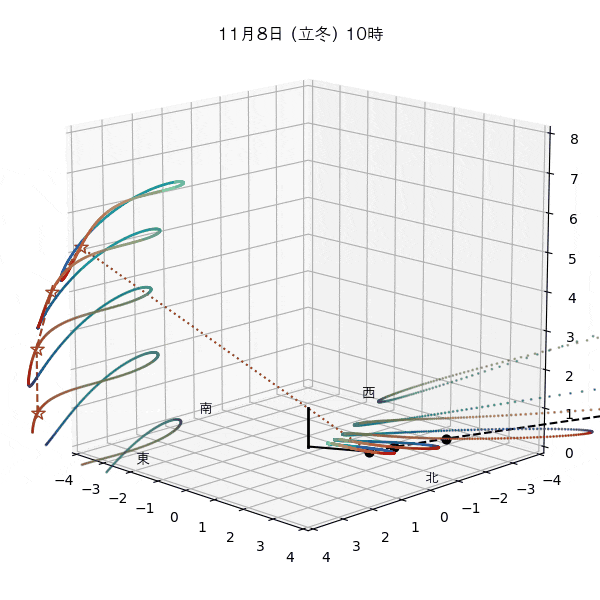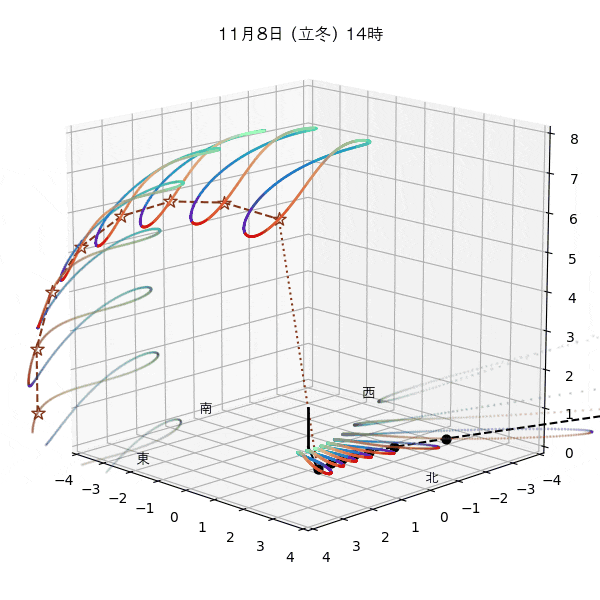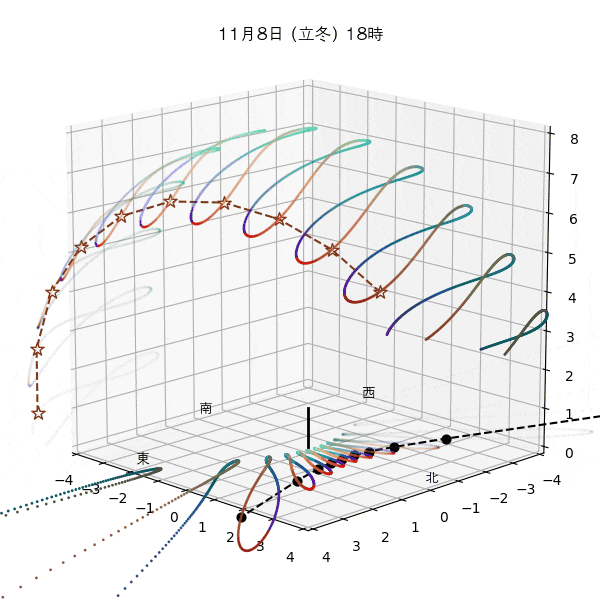
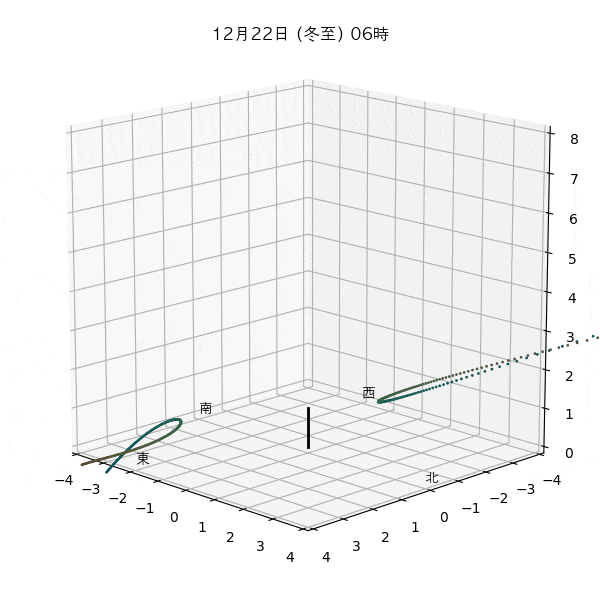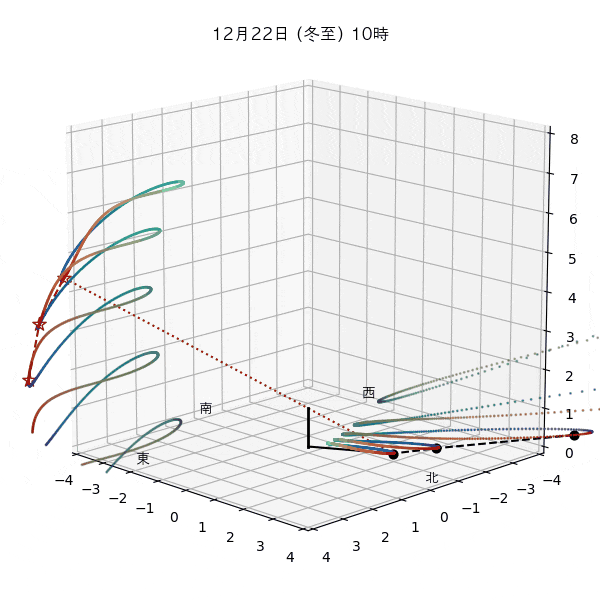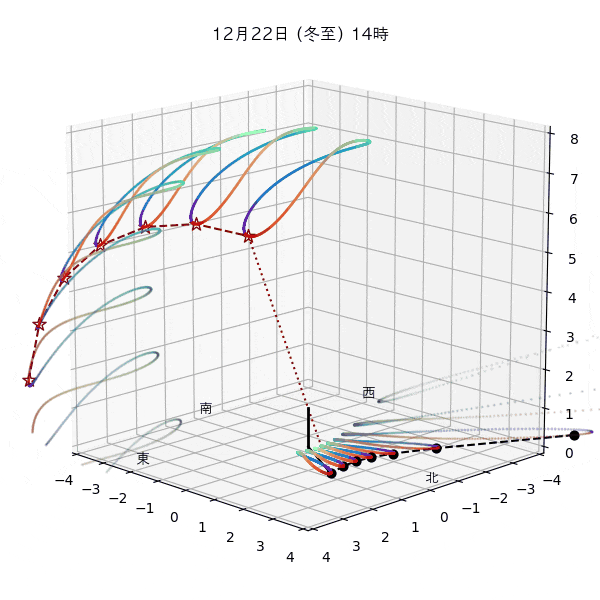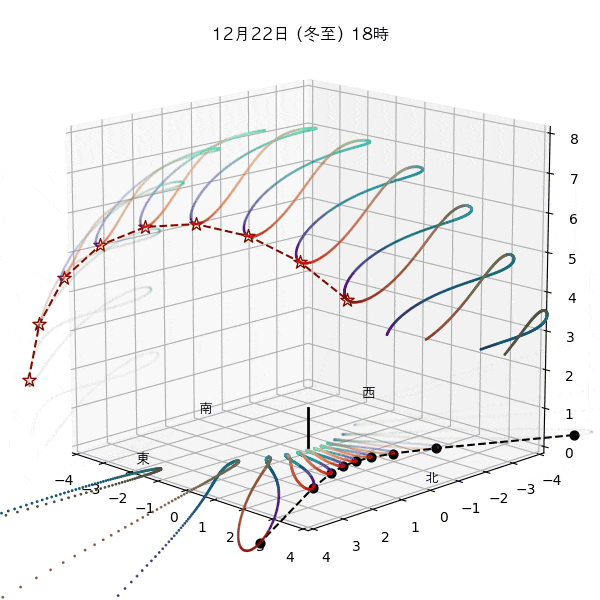
違う季節の太陽の軌道と柱の影

違う節気の一日中の太陽の天球上における見かけの軌道と柱の後ろに映る影を描いてみます。一時間毎のアナレンマもここで一緒に描きます。

import numpy as np
import matplotlib.pyplot as plt
import datetime
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun,SkyCoord,EarthLocation,AltAz
from mpl_toolkits.mplot3d import Axes3D
import imageio

koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1')
tt = np.arange(6,18+1,1) # 6時から18時まで1時間毎
toki = astropy.time.Time('2019-1-1') - koko.lon.value/15*u.hour + np.arange(365)*u.day + tt[:,None]*u.hour
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
az,alt = taiyou.az.value,taiyou.alt.value
x = -np.cos(np.radians(az))/np.tan(np.radians(alt))
y = -np.sin(np.radians(az))/np.tan(np.radians(alt))
sx,sy,sz = SkyCoord(az=az,alt=alt,distance=7,unit='deg',frame='altaz').cartesian.xyz.value
sz += 1

sekki = u'立春 春分 立夏 夏至 立秋 秋分 立冬 冬至'.split(' ')
tsukihi = ['2-4','3-21','5-6','6-22','8-8','9-23','11-8','12-22']
t_sekki = [int((astropy.time.Time('2019-%s'%t)-astropy.time.Time('2019-1-1')).value) for t in tsukihi]

for a,ts,sk in zip(t_sekki,tsukihi,sekki):
    cc = plt.get_cmap('rainbow')(np.arange(365)/364.)[:,:3]
    c = cc[a]*0.5
    gif = []
    for t0 in tt:
        j = t0-6
        o = (sz[:,a]>1)&(tt<=t0) # 仰俯角が0高い部分だけ描く
        fig = plt.figure(figsize=[6,6])
        ax = plt.axes([0,0,1,1],projection='3d',xlim=[-4,4],ylim=[-4,4],zlim=[0,8])
        ax.invert_yaxis()
        dt = datetime.datetime(*map(int,[2019]+ts.split('-')))
        plt.title(u'%d月%d日 (%s) %02d時'%(dt.month,dt.day,sk,t0),fontname='AppleGothic')
        ax.text(-2,4,0,u'東',fontname='AppleGothic')
        ax.text(-2,-4,0,u'西',fontname='AppleGothic')
        ax.text(-4,0,0,u'南',fontname='AppleGothic')
        ax.text(4,0,0,u'北',fontname='AppleGothic')
        ax.plot(sx[o,a],sy[o,a],sz[o,a],'--',color=c)
        ax.plot(x[o,a],y[o,a],0,'k--')
    
        for t in tt:
            if(t0<t):
                break # 過ぎた時間のアナレンマだけ描く
            i = t-6
            o = (sz[i]>1) # 仰俯角が0高い部分だけ描く
            alpha = ((12.-j+i)/12)**2
            ax.scatter(sx[i][o],sy[i][o],sz[i][o],c=cc[o]*(10-np.abs(10-(t-2)))/10,s=1,alpha=alpha)
            ax.scatter(x[i][o],y[i][o],0,c=cc[o]*(10-np.abs(10-(t-2)))/10,s=1,alpha=alpha)
            if(sz[i,a]>1):
                ax.scatter(sx[i,a],sy[i,a],sz[i,a],s=100,c='w',marker='*',edgecolor=c)
                ax.scatter(x[i,a],y[i,a],0,s=40,c='k')
        
        if(sz[j,a]>1):
            ax.plot([x[j,a],sx[j,a]],[y[j,a],sy[j,a]],[0,sz[j,a]],':',color=c)
            ax.plot([x[j,a],0],[y[j,a],0],[0,0],'k')
        
        plt.plot([0,0],[0,0],[0,1],'k',lw=2)
        ax.view_init(15,-45)
        fig.canvas.draw()
        gif.append(np.array(fig.canvas.renderer._renderer))
        plt.close()
    imageio.mimsave('a%03d.gif'%a,gif,fps=2)

a034.gif
a079.gif
a125.gif
a172.gif
a219.gif
a265.gif
a311.gif
a355.gif

太陽の高さを見ると、立春は立冬と同じで、春分は秋分と同じで、立夏は立秋と同じだとわおります。
ただし、平均太陽時と真太陽時の差があるため、太陽が昇り降りする時間は違うのです。

これはアナレンマにおける節気の位置から見てもわかります。例えば立春より立冬の方が西の方にあるので、立冬の方が日の出と日没が早いってわかります。

違う場所のアナレンマと日時計

一本柱を立て、その柱の影の違う季節での位置の表示を地面に描いたら、それは日時計に使えます。違う時間のアナレンマと、各節気の日の太陽の軌道を描いたら昼の間いつでも柱の影を見たらその時の時刻がわかります。

ただし、一般的に日時計によって表示する時刻はその時間帯に使う時計の標準時間ではなく、その場所の本当の平均太陽時です。

そのため、この記事で使われる時間も時間帯の標準時間ではなく、全部はその場の平均太陽時にしています。

地球のどこでも見えるアナレンマは大体同じく「８」の字の形をしているが、詳しくは違います。各場所で見えるアナレンマを描いて見てみます。

import numpy as np
import matplotlib.pyplot as plt
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun,SkyCoord,EarthLocation,AltAz
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.basemap import Basemap

# 地図を描く
fig = plt.figure(figsize=(6,6))
m = Basemap(70,-50,160,50)
m.drawcoastlines()
m.drawmeridians(np.arange(-180,181,30),labels=[0,0,1])
m.drawparallels(np.arange(-60,61,30),labels=[1])
latlong = {u'東京': EarthLocation(lat='35 40 30.78',lon='139 32 17.1'),
           u'汕頭': EarthLocation(lat='23 26 32',lon='116 35 20'),
           u'チエンマイ': EarthLocation(lat='18 35 26',lon='98 29 12'),
           u'新嘉坡': EarthLocation(lat=1.3342,lon=103.7357),
           u'バンドン': EarthLocation(lat='-6 49 28',lon='107 36 56'),
           u'キャンベラ': EarthLocation(lat='-35 19 13',lon='149 00 25'),
           u'南極': EarthLocation(lat=-90,lon=0),
           u'北極': EarthLocation(lat=90,lon=0)}
for chimei,koko in latlong.items():
    lon,lat = koko.lon.value,koko.lat.value
    plt.scatter(lon,lat,marker='.',color='r')
    plt.text(lon,lat,chimei,ha='right',fontname='AppleGothic',color='r')
plt.savefig('chizu.png')
plt.close()



sekki = u'立春 春分 立夏 夏至 立秋 秋分 立冬 冬至'.split(' ')
tsukihi = ['2-4','3-21','5-6','6-22','8-8','9-23','11-8','12-22']
t_sekki = [int((astropy.time.Time('2019-%s'%t)-astropy.time.Time('2019-1-1')).value) for t in tsukihi]
tt = np.arange(6,18+1,1) # 6時から18時まで1時間毎

for chimei,koko in latlong.items():
    toki = astropy.time.Time('2019-1-1') - koko.lon.value/15*u.hour + np.arange(365)*u.day + tt[:,None]*u.hour
    taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
    az,alt = taiyou.az.value,taiyou.alt.value
    x = -np.cos(np.radians(az))/np.tan(np.radians(alt))
    y = -np.sin(np.radians(az))/np.tan(np.radians(alt))
    sx,sy,sz = SkyCoord(az=az,alt=alt,distance=7,unit='deg',frame='altaz').cartesian.xyz.value
    sz += 1
    
    # 三次元で天球上の太陽と柱の影を描く
    fig = plt.figure(figsize=[6,12])
    ax = plt.axes([0,0.5,1,0.5],projection='3d',xlim=[-4,4],ylim=[-4,4],zlim=[0,8])
    plt.title('%s (%.4f, %.4f)'%(chimei,koko.lon.value,koko.lat.value),fontname='AppleGothic')
    ax.invert_yaxis()
    ax.text(-4,0,0,u'南',fontname='AppleGothic')
    ax.text(4,0,0,u'北',fontname='AppleGothic')
    
    o = (sz<1)
    x[o] = np.nan
    y[o] = np.nan
    sx[o] = np.nan
    sy[o] = np.nan
    sz[o] = np.nan
    
    for a in t_sekki:
        cc = plt.get_cmap('rainbow')(np.arange(365)/364.)[:,:3]
        c = cc[a]*0.5
        ax.plot(sx[:,a],sy[:,a],sz[:,a],'--',color=c)
        ax.plot(x[:,a],y[:,a],0,'k--')
        plt.plot([0,0],[0,0],[0,1],'k',lw=2)
        
    for t in tt:
        i = t-6
        ax.scatter(sx[i],sy[i],sz[i],c=cc*(10-np.abs(10-(t-2)))/10,s=1)
        ax.scatter(x[i],y[i],0,c=cc*(10-np.abs(10-(t-2)))/10,s=1)

    ax.view_init(15,-45)
    
    
    
    # 地面の影だけ描く
    plt.axes([0.05,0,0.93,0.5],xlim=[-7,7],ylim=[-6,6],aspect=1)
    plt.text(-5,0,u'西',fontname='AppleGothic',size=20,ha='center')
    plt.text(5,0,u'東',fontname='AppleGothic',size=20,ha='center')
    plt.text(0,-5,u'南',fontname='AppleGothic',size=20,ha='center')
    plt.text(0,5,u'北',fontname='AppleGothic',size=20,ha='center')
    
    for a in t_sekki:
        plt.plot(y[:,a],x[:,a],'--',color=plt.get_cmap('rainbow')(a/364.))
    plt.legend(sekki,prop={'family':'AppleGothic'},ncol=2,fancybox=1)
    plt.scatter(0,0,c='g')
        
    for t in tt:
        i = t-6
        plt.plot(y[i],x[i],'k')
    
    for t in tt[1:-1]:
        i = t-6
        mi = np.nanargmin(x[i])
        plt.text(y[i][mi],x[i][mi]-0.2,'%d'%t,color='k',ha='center',va='top',size=6)
        ma = np.nanargmax(x[i])
        plt.text(y[i][ma],x[i][ma]+0.2,'%d'%t,color='k',ha='center',va='bottom',size=6)
    plt.savefig('ana%s.png'%chimei)
    plt.close()

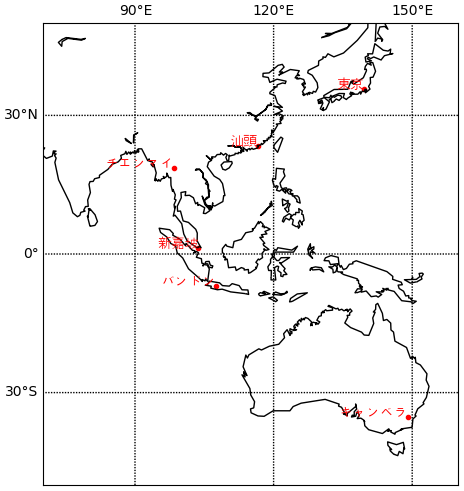
ここではまずbasemapというモジュールを使って各場所の位置を示す地図を描くのです。（basemapのインストールはちょっと難しいので、basemapがない場合これを無視していいのです。）

chizu.png

太陽の見える様子は緯度によるので、北から南まで違う緯度にある場所を選んだのです。

次はこれらの場所のアナレンマを表示しながら説明します。

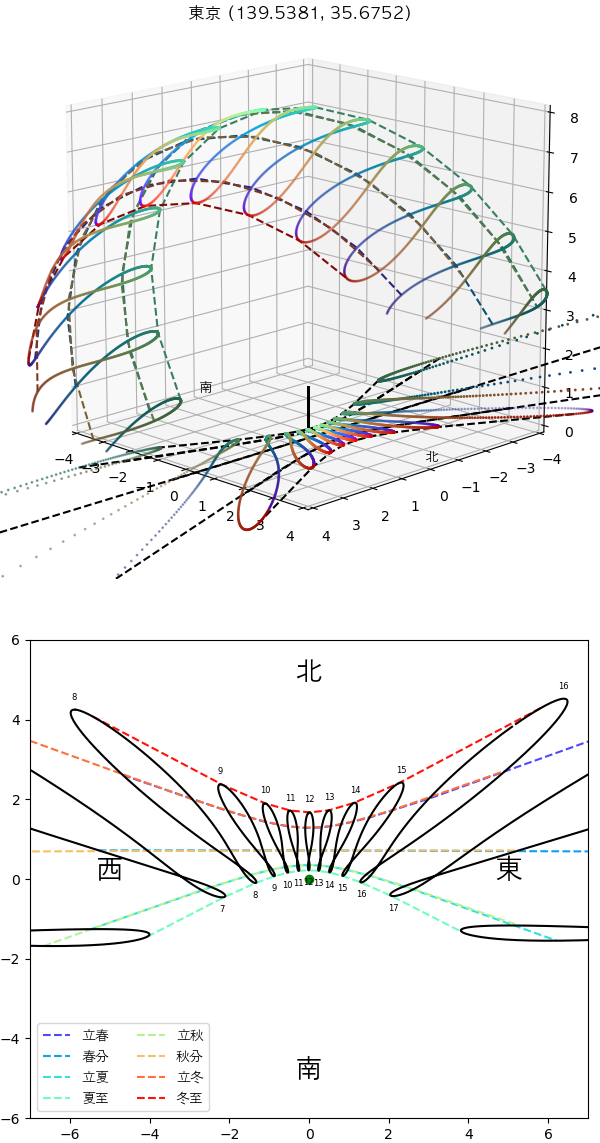
まずは日本東京都三鷹市の国立天文台です。北回帰線以北にあるため、夏至の正午の太陽は北の方にあります。

ana東京.png

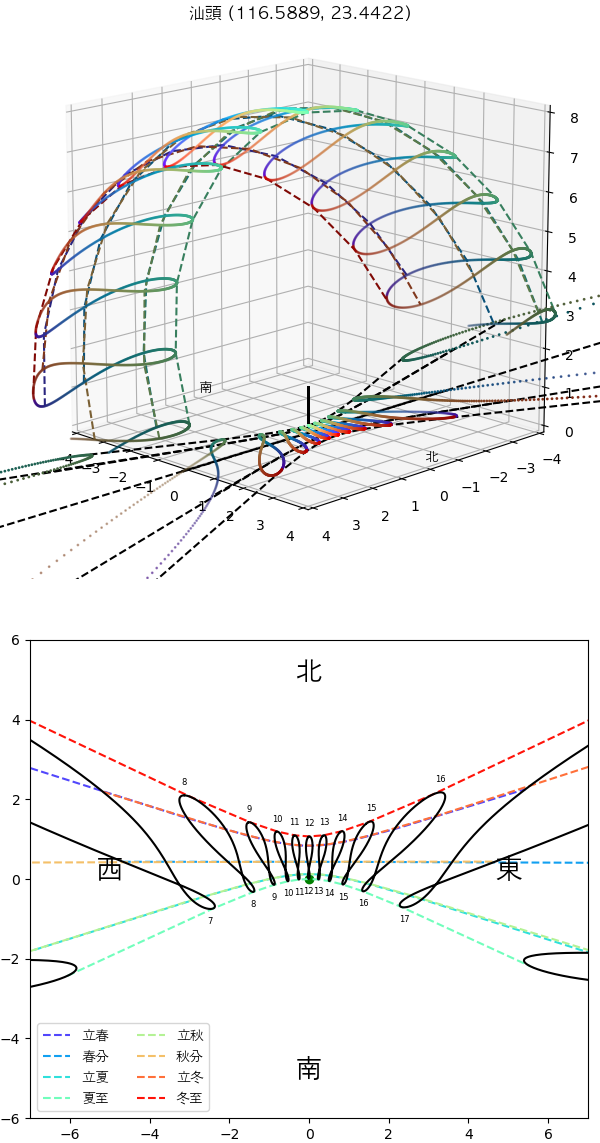
次は広東省汕頭市の北回帰線標誌塔。あそこにはちょうど北回帰線が通過するので、夏至の正午の太陽はちょうど天頂にあります。

ana汕頭.png

ちなみに中国では（台湾を含め）汕頭の他にも広州や嘉義や花蓮など北回帰線が通過する色んな場所に「北回帰線標誌」があるのです。

日本には北回帰線標誌のようなものがないが、台湾の嘉義県にある北回帰線標誌は日本統治時代から初めて建てられたものです。詳しくは https://ja.wikipedia.org/wiki/嘉義北回帰線標誌

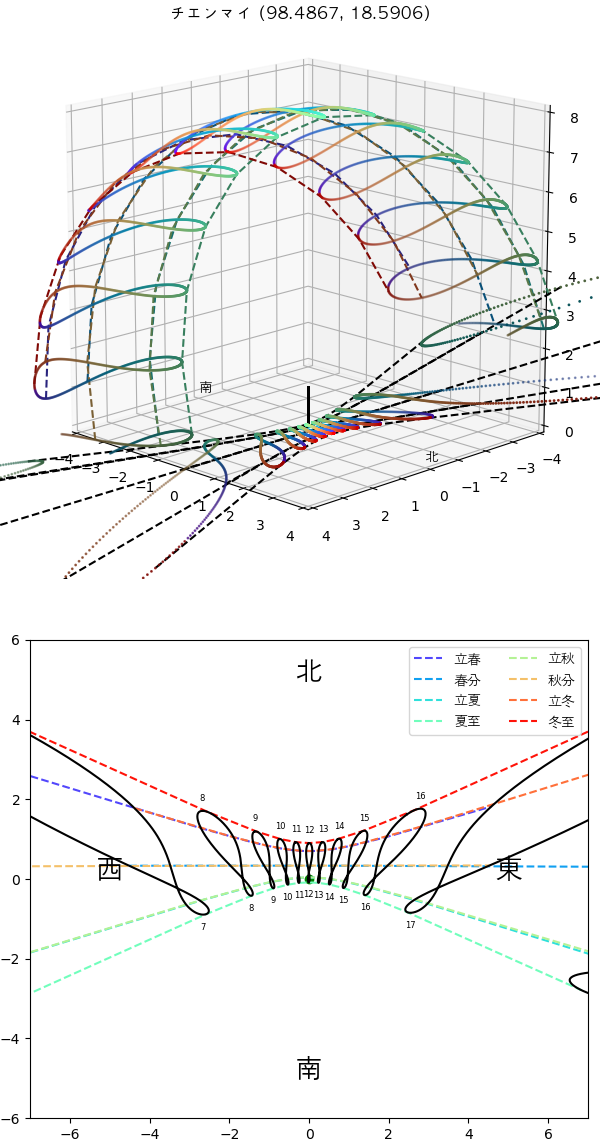
次はタイのチエンマイにあるタイ国立天文台（หอดูดาวแห่งชาติ）です。北回帰線以南にあるため、夏至の正午の太陽はやや南の方にあります。

anaチエンマイ.png

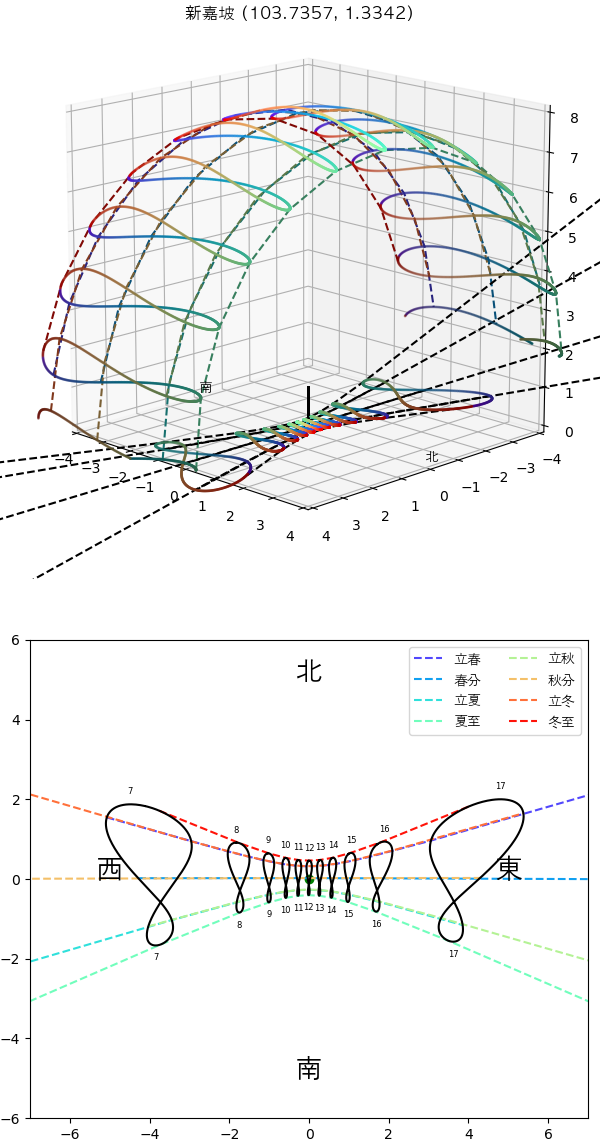
次はほぼ赤道にある新嘉坡（シンガポール）のサイエンス・センターです。ここでは太陽が天頂の近くに昇り、アナレンマはちょうど真ん中に置かれます。

ana新嘉坡.png

次は南半球の方。

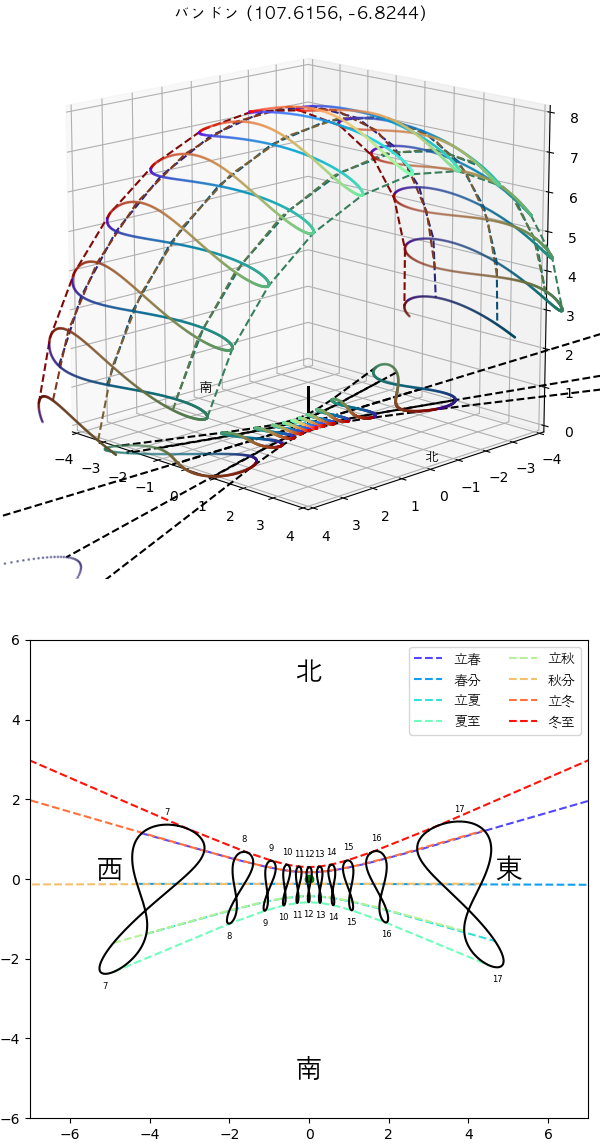
インドネシアのバンドンにあるボスカ天文台（Observatorium Bosscha）です。南回帰線以南にあるため冬至の正午の太陽はちょっと北の方にあります。

anaバンドン.png

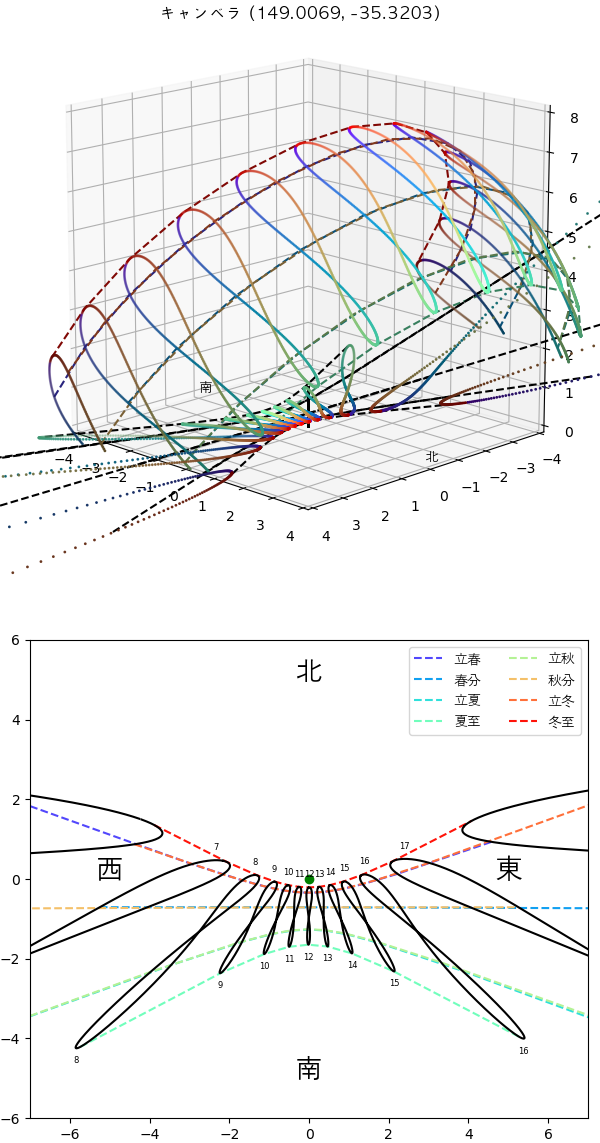
オーストラリアの首都であるキャンベラにあるストロムロ山天文台（Mount Stromlo Observatory）です。南回帰線以南にあるため冬至の正午の太陽はやや南の方にあります。

anaキャンベラ.png

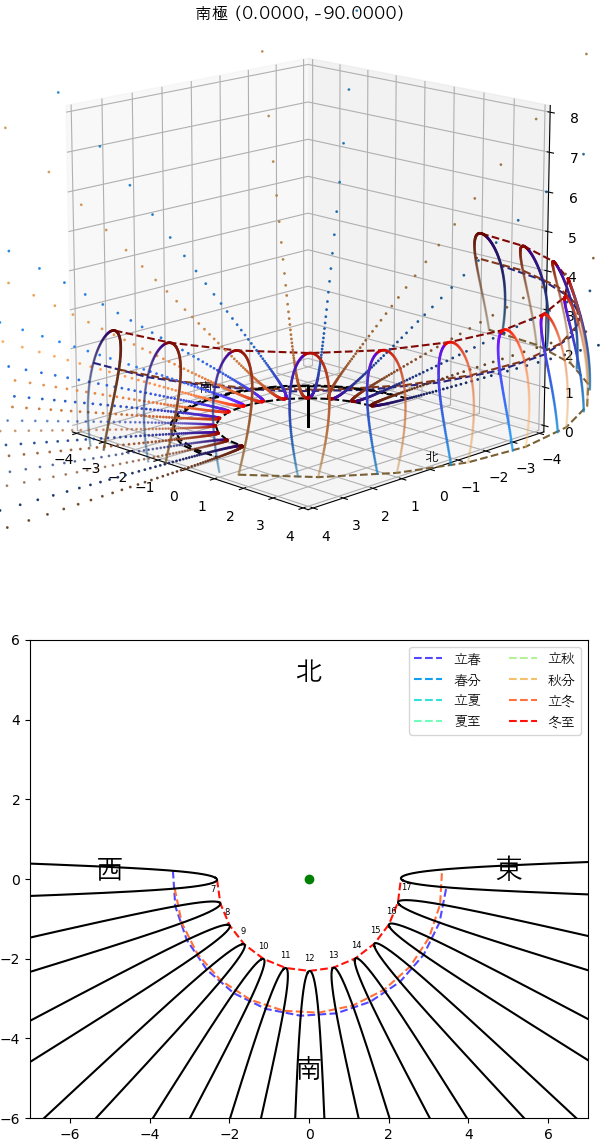
南極です。あこでは特別です。秋分と春分の日の間の半年は時間はずっと昼である一方、春分と秋分の日の間のもう半年はずっと夜です。だから何時のアナレンマでも半分しかないのです。

ana南極.png

ちなみにここで描いたのは6時から18時までのアナレンマだけで、実は19時から朝5時までも日没にならないので、アナレンマを描たければ同じく描けます。

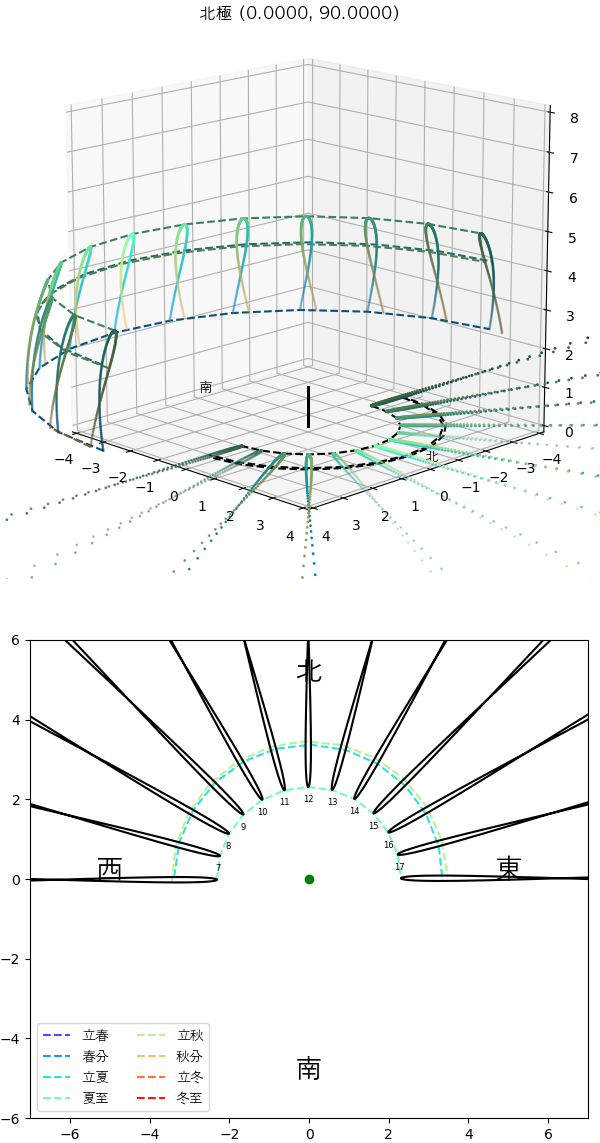
最後は北極です。大体は南極とは逆。

ana北極.png

終わりに

以上、アナレンマについて説明しながらastropyで実際に描いてみました。太陽の位置がわかったら色んなことができるのです。

4
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?