astropyから得られた太陽の位置を調べて日の出や日没の時間や昼の長さや季節の違いについて勉強してみたり

この記事ではastropyというpythonモジュールを使って太陽の位置を求めて、得られた太陽の位置を使って色んなことをやってみます。

はじめに

地球は太陽の周りを公転しているから太陽の見かける位置はいつも変わっていくものです。大昔から天文学者が太陽の変化を記録して移動の規則を求めて確定させて、それを基として季節の推測に使ってきたのです。

天文学によって太陽の位置を計算する方程式が確定されたので、今は天体観測をする時などには使われています。

太陽の位置の変化には色んな要因からできているため、それを計算することはとても複雑で難しいことですが、天文学のためのpythonモジュールであるastropyを使ったらだいぶ簡単になります。

太陽の位置を計算することはastropyの機能の一つです。astropyの中のget_sunという関数を使ったらすぐ特定の時間の太陽の位置をわかるので、すごく便利です。

astropyの使う例はこの前の記事でも色々ありました。

ここではget_sunを含めastropyの機能を駆使して色んなことをやってみます。

太陽の位置を求める方法

計算方法について複雑なのでここでは触れずに、astropyを使ってすぐ太陽の位置を求めます。

詳しい原理はこの記事などで読めます

例としてこの記事を書き終わった日である2019年5月16日の午後17時の時間の太陽の位置を求めることから始めます。

import datetime
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun

tz = astropy.time.TimezoneInfo(9*u.hour) # 時間帯を決める。
toki = datetime.datetime(2019,5,16,17,0,0,tzinfo=tz)
toki = astropy.time.Time(toki)
taiyou = get_sun(toki)

astropy.time.Timeというastropyの時間オブジェクトを使ったら時間に関する計算は簡単にできて便利です。これを作る方法はたくさんありますが、今回はdatetime.datetimeから変換します。
（このdatetimeはpythonの標準ライブラリに含められたモジュール）

astropy.time.Timeには時間帯の情報は含まれないので、まずastropy.time.TimezoneInfoを使って時間帯の決めたdatetime.datetimeを作って、それを使ってastropy.time.Timeを作ります。ここでは日本時間（+9）でいきます。

実に言うと最初から時間帯を使わずにdatetime.datetime(2019,5,14,17-9,0,0)と入力したら結果は同じですが、こうやって日本の時間を直接入力する方が直感的だと思います。

print(taiyou)
print(taiyou.get_constellation())

<SkyCoord (GCRS: obstime=2019-05-16 08:00:00, obsgeoloc=(0., 0., 0.) m, obsgeovel=(0., 0., 0.) m / s): (ra, dec, distance) in (deg, deg, AU)
    (52.56895829, 18.99532917, 1.01098867)>
Taurus

時間は08:00って表示されていますが、これはグリニッジでの標準時間です、日本とは9時間違うからです。

こうやって太陽の赤経と赤緯はわかりますが、これを見えるだけでどこになのかはわかりにくいので、get_constellationを使って、おうし座（Taurus）にあるとわかりました。五月の後半だから金牛宮です。

一年間の太陽の位置

astropy.time.Timeはnumpyのndarrayみたいに扱いできるので、たくさんの値をndarrayとして入力することもできます。こうやって一年間の太陽の位置を一気に求められるのでかなり便利です。

太陽と地球との距離

一年間の間に太陽の距離はどんなに変化するか見てみます。

import numpy as np
import matplotlib.pyplot as plt

tz = astropy.time.TimezoneInfo(9*u.hour)
toki = datetime.datetime(2019,1,1,12,0,0,tzinfo=tz)
toki = astropy.time.Time(toki) + np.arange(365)*u.day

taiyou = get_sun(toki)
plt.scatter(toki.value,taiyou.distance.value,c=np.arange(365),s=1,cmap='rainbow')
chikai_toki = toki.value[taiyou.distance.value.argmin()]
tooi_toki = toki.value[taiyou.distance.value.argmax()]
plt.axvline(chikai_toki,color='k',ls=':')
plt.axvline(tooi_toki,color='k',ls=':')
plt.text(chikai_toki,1,'%s\n%.3f AU'%(chikai_toki.date(),taiyou.distance.value.min()))
plt.text(tooi_toki,1,'%s\n%.3f AU'%(tooi_toki.date(),taiyou.distance.value.max()))
plt.ylabel(u'距離 (AU)',fontname='AppleGothic')
plt.show()

1（AU）ってのは天文単位であり、太陽と地球の平均距離と定義されたが、地球の軌道は楕円なので一年間の間で少しずつ変わっていくので、1AUより遠い時期もあれば近い時期もあるのです。

2019年では最も近いのは1月3日に0.983AUくらいで、最も遠いのは7月5日に1.017AUくらいです。毎年はやや違って最も近いのは1月4日である年もあります。

平均値や標準偏差を計算してみます。

print('平均値　=　%s'%taiyou.distance.mean())
print('中央値　=　%s'%np.median(taiyou.distance))
print('最小　　=　%s'%taiyou.distance.min())
print('最大　　=　%s'%taiyou.distance.max())
print('標準偏差=　%s'%taiyou.distance.std())

平均値　=　1.0001554332381795 AU
中央値　=　1.000274903167035 AU
最小　　=　0.9833011754382442 AU
最大　　=　1.0167542177816637 AU
標準偏差=　0.011824130385267981 AU

平均値は案の定ほぼ1AUでした。

太陽の通う星座

一年間の間に太陽は何日間どの星座にあるか調べます。

seiza = taiyou.get_constellation()
print('\n'.join(sorted({'%s: %d'%(s,list(seiza).count(s)) for s in set(seiza)},key=lambda x:int(x.split(':')[1]),reverse=True)))

Virgo: 44
Pisces: 38
Taurus: 38
Leo: 37
Sagittarius: 33
Gemini: 30
Capricornus: 27
Aries: 25
Aquarius: 24
Libra: 23
Cancer: 21
Ophiucus: 18
Scorpius: 7

太陽の通る星座は「黄道十二宮」と呼ばれていますが、見ての通り太陽の位置は12ではなく13もの星座を通るのです。昔からへびつかい座(Ophiucus)だけは黄道十二宮に含められていないのです。

それと、黄道十二宮は12等分に分けられることが多いが、実際に太陽のかかる時間は星座によって違います。さそり座(Scorpius)が一番短いです。

観測地から見える太陽の位置

次は空を見上げたらどこに太陽が見えるか調べる方法です。まずは観測する場所を決めて、その場所の地平座標に変換する必要があります。地平座標は観測する位置次第に変わるのです。ここでは東京都三鷹市国立天文台の位置を使います。

from astropy.coordinates import EarthLocation

koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1')
print(koko.geodetic)
print(koko.lon)
print(koko.lat)
print(koko.height)

GeodeticLocation(lon=<Longitude 139.53808333 deg>, lat=<Latitude 35.67521667 deg>, height=<Quantity 1.18151372e-09 m>)
139d32m17.1s
35d40m30.78s
1.18151372121186e-09 m

EarthLocationは地上の場所を代表するオブジェクトです。実は場所の海抜も決める必要があるが、あまり影響がないので、ここでは無視します。高さを入れない場合0に近い値となります。

場所を指定したら、次はその場所とその時間での太陽の位置を求めます。

from astropy.coordinates import AltAz

toki = astropy.time.Time(datetime.datetime(2019,5,16,17,0,0)) - 9*u.hour
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
print(taiyou)
print(taiyou.az) # 天球での方位角
print(taiyou.alt) # 天球での仰俯角
print(taiyou.distance) # 距離
print(taiyou.distance.au) # au単位での距離

<SkyCoord (AltAz: obstime=2019-05-16 08:00:00, location=(-3946538.41739037, 3366128.13547354, 3698977.52925049) m, pressure=0.0 hPa, temperature=0.0 deg_C, relative_humidity=0.0, obswl=1.0 micron): (az, alt, distance) in (deg, deg, m)
    (280.5587648, 18.53482874, 1.5123973e+11)>
280d33m31.5533s
18d32m05.3835s
151239730424.7721 m
1.0109751543727827

AltAzは地平座標のオブジェクトです。こうやって太陽の天球での方位角と仰俯角と距離がわかります。地平線座標に変換したら表示する距離はAUではなく、メートルになりますが、.auをつけたらすぐにAU単位の値を見ることができます。

方位角は北では0度で西では270度です。17時は午後だから方位角280度でほぼ西の方にあることは合理だとわかります。もうすぐ日没する時間だから仰俯角もたった18度です。

一日間の太陽の仰俯角を見てみます。

import matplotlib as mpl

toki = astropy.time.Time('2019-5-16') - 9*u.hour
toki += np.linspace(0,24,1441)*u.hour
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
plt.plot((toki+9*u.hour).datetime,taiyou.alt.value,'r')
plt.gca().xaxis.set_major_formatter(mpl.dates.DateFormatter('%H:%M'))
plt.axhline(0,ls='--',color='k') # 日の出と日没の線
takasa = taiyou.alt.max().value # 一番高い高さ
takai_toki = (toki[taiyou.alt.argmax()]+9*u.hour).datetime # 一番高い時間
plt.scatter(takai_toki,takasa)
plt.text(takai_toki,takasa,'%s\n%.2f度'%(takai_toki.strftime('%H:%M'),takasa),fontname='AppleGothic',va='top',ha='center')
plt.xlabel(u'時間',fontname='AppleGothic')
plt.ylabel(u'太陽の仰俯角 (度)',fontname='AppleGothic')
plt.show()

こうやって一日中の太陽が昇り降りするとわかります。

標準時間との差

上のグラフを見たら太陽が一番高く昇るのは12時ではないとわかるのです。12時は一日の中心で、普通に考えると太陽がちょうど南中のところで一番高く昇る時間であるはずですが、必ずしもそうではなかったです。

原因はこの「12時」はただ時計の中の時間ですが、全国の経度は違うものの同じ時計を使っているのです。例えば日本の標準時間は135度に決まっているが、東京の本当の経度は139~140なので地域の本当の真昼は時計の12時より早いです。

実際に135度の線が通過するのは兵庫県などのところです。

兵庫からそんなに遠くないので多分東京の場合ではその違いはあまり認識しないかもしれないが、中国などの国では1時間以上標準時間との差がある地域がいっぱいあります。中国の標準時間は東岸の方にある杭州市を通過する120度の時間に決まりますが、チベットなど西にある地域では標準時間より2時間よりも遅いです。

場所の本当の真昼の時間にするためにはこう書き直します。

toki = astropy.time.Time('2019-5-16') - koko.lon.value/15*u.hour

東の139°32′17″にある国立天文台の時間はグリニッジ標準時間との本当の差は

print(koko.lon.value/15*u.hour)

9.302538888888888 h

9時間とは0.3時間の差、つまり18分くらいです。

でもさっきのグラフでできた最大値は11:38のところにあります。12:00との差は18分ではなく、20分以上です。

実は地球の公転軌道は円ではなく楕円であるため、公転の速度は一定ではなく季節によって変わっていくものです。そのため一日の長さは実際には同じではないはずですが、毎日が同じ24時間の長さにするために平均太陽時という時間が決められ、これを使うことで私達が普通に毎日の「一日」という時間は同じように認識していけるわけです。毎日の長さは同じになていることは便利ですが、それは原因として、平均太陽時と真太陽時の差が発生して、毎日の真の正午の時間は違うのです。

もっと詳しくはこの記事で http://koyomi8.com/reki_doc/doc_0508.htm

一年間見かける太陽の位置の変化

一年間で一時間毎の太陽の見かける位置をプロットしてみます。

nen = 2019 # 年
nissuu = 365 # その年に日数
koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1') # 場所
jisa = 9 # 時間帯とグリニッジとの時差

tt = np.arange(4,19+1)
toki = astropy.time.Time('%d-1-1'%nen) - jisa*u.hour + np.arange(nissuu)*u.day + tt[:,None]*u.hour
taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))

plt.figure(figsize=[6,6])
ax = plt.subplot(211,xlim=[toki.min().datetime,toki.max().datetime])
for i,(t,a) in enumerate(zip(tt,taiyou.alt.value)):
    c = color=plt.get_cmap('jet')(i/15.)
    plt.plot(toki[i].datetime,a,color=c,label=t)
plt.legend(ncol=2,loc=1,prop={'size':8})
plt.axhline(0,color='k')
plt.grid(ls='--')
plt.ylabel(u'仰俯角',fontname='AppleGothic')
ax.xaxis.set_major_formatter(mpl.dates.DateFormatter(u''))

ax = plt.subplot(212,xlim=[toki.min().datetime,toki.max().datetime])
for i,(t,a) in enumerate(zip(tt,taiyou.az.value)):
    c = color=plt.get_cmap('jet')(i/15.)
    plt.plot(toki[i].datetime,a,color=c,label=t)
plt.axhline(180,color='k')
plt.grid(ls='--')
plt.ylabel(u'方位角',fontname='AppleGothic')
ax.xaxis.set_major_formatter(mpl.dates.DateFormatter(u'%m月\n%d日'))
plt.xticks(fontproperties=mpl.font_manager.FontProperties(family='AppleGothic'))
plt.tight_layout()
plt.show()

こうやって一年間日の出や日没の時間は季節によって変わっていくとわかります。地球の自転軸が偏っているため、太陽の昇る高さ及び昼と夜の長さは日によって違って、これは季節が起きる原因です。

方位角は180度であるところは真南なので、方位角を見ると太陽が南中する時間は11時と12時の間に揺れているとわかります。

仰俯角は0度であるところは日の出と日没の時なので、仰俯角を見ると日の出の時間は4時から7時までの間に、日没の時間は16時と19時の間に揺れているとわかります。
（実際に太陽の見かけの大きさを含めると0.25度くらいになりますがここでは簡単のために0度を使います）

太陽が南中する時間と日の出と日没の時間と昼の長さ

次は一年間の毎日の

• 日の出
• 真の正午（太陽が南中する時間）
• 日没
• 昼の長さ
  これらを求めてみます。

get_sunを使ったら太陽の位置がわかるが、いつ仰俯角が0になる時間なのか直接求める方法はないので、色んな時間を試して0が見つかるまで繰り返すという方法を使うのです。

この方法についてはこの記事で使われたのです。

もともとget_sunを使い始めてみたのは、astropyを使って日の出の時間を求める方法を書いたこの記事を読んだのはきっかけでした。

scipyのoptimize.bisectを使って二分法で答えを求めます。

二分法の原理と使い方はこの記事に説明があります。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import astropy.time
import astropy.units as u
from astropy.coordinates import get_sun,EarthLocation,AltAz
from scipy import optimize
import datetime

def az180(t):
    t = astropy.time.Time(t,format='mjd')
    return get_sun(t).transform_to(AltAz(obstime=t,location=koko)).az.value-180

def alt0(t):
    t = astropy.time.Time(t,format='mjd')
    return get_sun(t).transform_to(AltAz(obstime=t,location=koko)).alt.value

nen = 2019 # 年
nissuu = 365 # その年に日数
koko = EarthLocation(lat='35 40 30.78',lon='139 32 17.1') # 場所
jisa = 9 # 時間帯とグリニッジとの時差

jisa = astropy.time.TimeDelta(jisa*u.hour)
t0 = astropy.time.Time('%d-1-1'%nen)-jisa

hinode = [] # 日の出
t1 = (t0+4.0*u.hour).mjd
t2 = (t0+7.5*u.hour).mjd
for hi in np.arange(nissuu):
    t = optimize.bisect(alt0,t1,t2)
    t1 = t+0.996
    t2 = t+1.004
    t = (astropy.time.Time(t,format='mjd')+jisa).datetime
    print(t.strftime(u'%m月%d日'))
    hinode.append(t)

nanchuu = [] # 南中
t1 = (t0+11.0*u.hour).mjd
t2 = (t0+12.5*u.hour).mjd
for hi in np.arange(nissuu):
    t = optimize.bisect(az180,t1,t2)
    t1 = t+0.996
    t2 = t+1.004
    t = (astropy.time.Time(t,format='mjd')+jisa).datetime
    nanchuu.append(t)
    print(t.strftime(u'%m月%d日'))

nichibotsu = [] # 日没
t1 = (t0+16.0*u.hour).mjd
t2 = (t0+19.5*u.hour).mjd
for hi in np.arange(nissuu):    
    t = optimize.bisect(alt0,t1,t2)
    t1 = t+0.996
    t2 = t+1.004
    t = (astropy.time.Time(t,format='mjd')+jisa).datetime
    nichibotsu.append(t)
    print(t.strftime(u'%m月%d日'))



tt = (astropy.time.Time('%d-1-1'%nen)+np.arange(nissuu)*u.day).datetime # 一年間の毎日

hirujikan = [datetime.datetime(nen,1,1)+(b-d) for d,b in zip(hinode,nichibotsu)] # 昼の長さ
hinode = [x.time() for x in hinode]
nanchuu = [x.time() for x in nanchuu]
nichibotsu = [x.time() for x in nichibotsu]

plt.figure(figsize=[7,12])
ax = plt.subplot(411,xlim=[tt.min(),tt.max()],ylabel='')
plt.plot(tt,hinode)
mi = np.argmin(hinode) # 最小値の時間
ma = np.argmax(hinode) # 最大値の時間
plt.scatter(tt[mi],hinode[mi],c='g',marker='.')
plt.scatter(tt[ma],hinode[ma],c='r',marker='.')
plt.text(tt[mi],hinode[mi],u'%d月%d日 \n%d:%d:%d'%(tt[mi].month,tt[mi].day,hinode[mi].hour,hinode[mi].minute,hinode[mi].second),fontname='AppleGothic',va='bottom')
plt.text(tt[ma],hinode[ma],u'%d月%d日 \n%d:%d:%d'%(tt[ma].month,tt[ma].day,hinode[ma].hour,hinode[ma].minute,hinode[mi].second),fontname='AppleGothic',va='top')
plt.title(u'日の出',fontname='AppleGothic')
plt.xticks([])

ax = plt.subplot(412,xlim=[tt.min(),tt.max()],ylabel='')
plt.plot(tt,nanchuu)
mi = np.argmin(nanchuu)
ma = np.argmax(nanchuu)
plt.scatter(tt[mi],nanchuu[mi],c='g',marker='.')
plt.scatter(tt[ma],nanchuu[ma],c='r',marker='.')
plt.text(tt[mi],nanchuu[mi],u'%d月%d日 \n%d:%d:%d'%(tt[mi].month,tt[mi].day,nanchuu[mi].hour,nanchuu[mi].minute,nanchuu[mi].second),fontname='AppleGothic',va='bottom',ha='center')
plt.text(tt[ma],nanchuu[ma],u'%d月%d日 \n%d:%d:%d'%(tt[ma].month,tt[ma].day,nanchuu[ma].hour,nanchuu[ma].minute,nanchuu[mi].second),fontname='AppleGothic',va='top',ha='center')
plt.title(u'正午',fontname='AppleGothic')
plt.xticks([])

ax = plt.subplot(413,xlim=[tt.min(),tt.max()],ylabel='')
plt.plot(tt,nichibotsu)
mi = np.argmin(nichibotsu)
ma = np.argmax(nichibotsu)
plt.scatter(tt[mi],nichibotsu[mi],c='g',marker='.')
plt.scatter(tt[ma],nichibotsu[ma],c='r',marker='.')
plt.text(tt[mi],nichibotsu[mi],u'%d月%d日 \n%d:%d:%d'%(tt[mi].month,tt[mi].day,nichibotsu[mi].hour,nichibotsu[mi].minute,nichibotsu[mi].second),fontname='AppleGothic',va='bottom',ha='right')
plt.text(tt[ma],nichibotsu[ma],u'%d月%d日 \n%d:%d:%d'%(tt[ma].month,tt[ma].day,nichibotsu[ma].hour,nichibotsu[ma].minute,nichibotsu[mi].second),fontname='AppleGothic',va='top',ha='right')
plt.title(u'日沒',fontname='AppleGothic')
plt.xticks([])

ax = plt.subplot(414,xlim=[tt.min(),tt.max()],ylabel='')
plt.plot(tt,hirujikan)
mi = np.argmin(hirujikan)
ma = np.argmax(hirujikan)
plt.scatter(tt[mi],hirujikan[mi],c='g',marker='.')
plt.scatter(tt[ma],hirujikan[ma],c='r',marker='.')
plt.text(tt[mi],hirujikan[mi],u'%d月%d日 \n%d:%d:%d時間'%(tt[mi].month,tt[mi].day,hirujikan[mi].hour,hirujikan[mi].minute,hirujikan[mi].second),fontname='AppleGothic',va='bottom',ha='right')
plt.text(tt[ma],hirujikan[ma],u'%d月%d日 \n%d:%d:%d時間'%(tt[ma].month,tt[ma].day,hirujikan[ma].hour,hirujikan[ma].minute,hirujikan[ma].second),fontname='AppleGothic',va='top',ha='right')
plt.title(u'日の出~日沒',fontname='AppleGothic')
ax.xaxis.set_major_formatter(mpl.dates.DateFormatter(u'%m月\n%d日'))
ax.xaxis.set_major_locator(mpl.dates.DayLocator(interval=29))
plt.xticks(fontproperties=mpl.font_manager.FontProperties(family='AppleGothic'))
ax.yaxis.set_major_formatter(mpl.dates.DateFormatter(u'%H時間'))
ax.yaxis.set_major_locator(mpl.dates.MinuteLocator(0))
plt.yticks(fontproperties=mpl.font_manager.FontProperties(family='AppleGothic'))
plt.tight_layout(0)
plt.show()

二十四節気について

グラフを見たら2019年で昼が一番長いと一番短いのは6月22日と12月22日だとわかります。

昼が一番長い日は**夏至の日であり、一番間近い日は冬至**の日です。

そして昼時間はちょうど12時間である日は二つあります。それは春分の日と秋分の日です。

tt[np.abs((astropy.time.Time(hirujikan)-astropy.time.Time('2019-1-1 12:00')).value).argsort()[:2]]

array([datetime.datetime(2019, 3, 21, 0, 0),
       datetime.datetime(2019, 9, 23, 0, 0)], dtype=object)

これで2019年の春分と秋分の日は3月21日と9月23日だとわかります。

春分と夏至と秋分と冬至は、毎年の時間は24等分に分ける**二十四節気**の一員です。

毎年の節気の時間は完全に同じではないが、大体同じ日で、1〜2日くらいの差があるだけです。

二十四節気に関する詳細はこのサイトで http://koyomi8.com/reki_doc/doc_0130.htm

夏至は「一番昼の長い日」だというと、その日は一番朝が早くて夜が遅い日だと想像する人も少なくないかもしれないが、実際にはそうではなのです。上述の日の出と日没時間を表示するグラフを見たら、一番朝が早いのは6月13日で、一番夜が遅いのは6月29日だとわかります。

それと、一番朝が遅いのは冬至ではなく、1月17日で、一番夜が遅いのは11月4日です。

原因は平均太陽時と真太陽時の違いにあります。夏至である6月22日の昼が一番長いが、真太陽時は6月13日よりも遅いので、日の出の時間はちょっと遅くて、6月13日の方が早いわけです。

アナレンマについて

南中の時間のクラフを見たら面白い姿になっているとわかります。これは地球の偏った自転軸と楕円の公転軌道の組み合わせでできたものです。そして毎日同じ時間の太陽の見かける位置を空中でプロットしてみたら「８」の字に見えて、アナレンマと呼ばれます。

アナレンマの話は次の記事で描いてあります

太陽が天頂にある日

日本のように温帯にある地域（北回帰線以北）では太陽が一番高い夏至の日でも天頂にまでは辿り着くことはないのですが、熱帯の地域（北回帰線と南回帰線との間）では太陽が天頂まで昇ることができます。天頂に昇る機会は春分と秋分の間にあって一年で二度もあります。

それが何の日か探してみます。今回は例として場所はタイのチエンマイにあるタイ国立天文台（หอดูดาวแห่งชาติ）にします。経度は98°29′12″、緯度は18°35′26″だから北回帰線以南です。

毎日太陽が南中する時の仰俯角を探して最大になる時を求めてみます。

nen = 2019
nissuu = 365
koko = EarthLocation(lat='18 35 26',lon='98 29 12')
jisa = 7

jisa = astropy.time.TimeDelta(jisa*u.hour)
t0 = astropy.time.Time('%d-1-1'%nen)-jisa
t1 = (t0+10*u.hour).mjd
t2 = (t0+14*u.hour).mjd
gyoufu = []
for hi in np.arange(nissuu):
    t = optimize.bisect(az180,t1,t2)
    t1 = t+0.996
    t2 = t+1.004
    t = (astropy.time.Time(t,format='mjd'))
    taiyou = get_sun(t).transform_to(AltAz(obstime=t,location=koko))
    gyoufu.append(taiyou.alt.value)
    print(t.strftime(u'%m月%d日'),taiyou.az.value,taiyou.alt.value)

gyoufu = np.array(gyoufu)
tt = (astropy.time.Time('%d-1-1'%nen)+np.arange(nissuu)*u.day)
ax = plt.gca(xlim=[tt.datetime.min(),tt.datetime.max()])
plt.plot(tt.datetime,gyoufu)
mi = np.argmin(gyoufu) # 最小値の日
ma = gyoufu.argsort()[[-1,-2]] # 二つ最大値の日を求める
plt.scatter(tt[mi].datetime,gyoufu[mi],c='g',marker='.')
plt.scatter(tt[ma].datetime,gyoufu[ma],c='r',marker='.')
plt.text(tt[mi].datetime,gyoufu[mi],u'%d月%d日 \n%.3f度'%(tt[mi].datetime.month,tt[mi].datetime.day,gyoufu[mi]),fontname='AppleGothic',va='bottom',ha='center')
for i in [0,1]:
    plt.text(tt[ma[i]].datetime,gyoufu[ma[i]],u'%d月%d日 \n%.3f度'%(tt[ma[i]].datetime.month,tt[ma[i]].datetime.day,gyoufu[ma[i]]),fontname='AppleGothic',va='top',ha='center')
plt.ylabel(u'仰俯角',fontname='AppleGothic')
ax.xaxis.set_major_formatter(mpl.dates.DateFormatter(u'%m月\n%d日'))
plt.xticks(fontproperties=mpl.font_manager.FontProperties(family='AppleGothic'))
plt.show()

見ての通り冬至の日は一番太陽の昇りが低い日ってことに代わりはないが、夏至の日は一番高い日ではないのですが、5月14日と7月30日はちょうど太陽が天頂を通る日です。

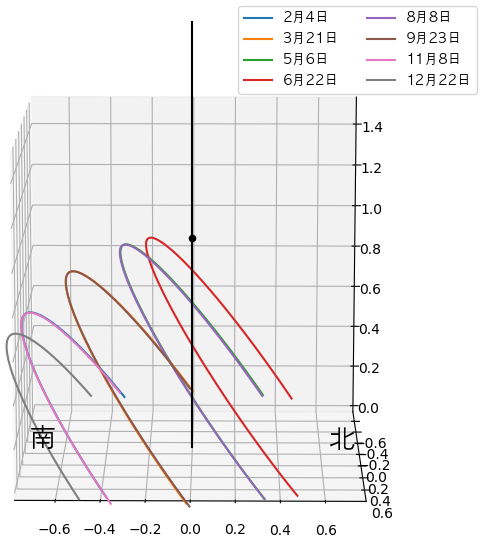
原因をわかりやすくなるように三次元での太陽の天球上で見かける軌道を見たらいいです。二十四節気の中の8つの節気での太陽の軌道を描いてみます。

2019年で節気はそれらの日に当たります。（日本時間で）

• 立春：2月4日
• 春分：3月21日
• 立夏：5月6日
• 夏至：6月22日
• 立秋：8月8日
• 秋分：9月23日
• 立冬：11月8日
• 冬至：12月22日

東京とチエンマイの場合を両方共を描いて比べてみます。

from mpl_toolkits.mplot3d import Axes3D
from astropy.coordinates import SkyCoord

sekki = u'立春 春分 立夏 夏至 立秋 秋分 立冬 冬至'.split(' ') # 節気の名前
tsukihi = ['2-4','3-21','5-6','6-22','8-8','9-23','11-8','12-22'] # 節気の月日
hi = np.array([[int((astropy.time.Time('2019-%s'%t)-astropy.time.Time('2019-1-1')).value) for t in tsukihi]]).T
leg = [ts.replace(u'-',u'月')+u'日' for ts in tsukihi]

for jisa,koko in zip([9,7],[EarthLocation(lat='35 40 30.78',lon='139 32 17.1'),EarthLocation(lat='18 35 26',lon='98 29 12')]):
    toki = astropy.time.Time('2019-1-1') - jisa*u.hour + np.linspace(4*60,20*60,101)*u.minute + hi*u.day
    taiyou = get_sun(toki).transform_to(AltAz(obstime=toki,location=koko))
    az,alt = taiyou.az.value,taiyou.alt.value # 方位角と仰俯角
    xx,yy,zz = SkyCoord(az=az,alt=alt,unit='deg',frame='altaz').cartesian.xyz.value # 直交座標に変換
    # 三次元プロット
    plt.figure(figsize=[6,6])
    ax = plt.axes([0,0,1,1],projection='3d',xlim=[-0.75,0.75],ylim=[-0.75,0.75],zlim=[0,1.5])
    ax.invert_yaxis() # 地平座標でのy本来のxyz座標とは逆なので、y軸を逆にする必要がある
    for x,y,z in zip(xx,yy,zz):
        ax.plot(x[z>0],y[z>0],z[z>0]) # 地上にある軌道だけ描く
    ax.scatter(0,0,1,c='k')
    ax.text(-0.7,0,0,u'南',fontname='AppleGothic',size=20,ha='center')
    ax.text(0.7,0,0,u'北',fontname='AppleGothic',size=20,ha='center')
    ax.plot([0,0],[0,0],[0,2],'k')
    plt.legend(leg,prop={'family':'AppleGothic'},ncol=2,fancybox=1)
    plt.show()

東京の場合、緯度が23.5より高いので夏至である6月22日は太陽が一番高く登っても天頂にまで達していないのです。

チエンマイの場合、緯度が23.5より低いので夏至の日には真昼の太陽が天頂よりもっと北の方まで通り過ぎるため仰俯角は低くなります。

夏至は一番昼の長い日であることは変わりはないが、太陽の仰俯角は別の問題です。

太陽が高く昇るほど天気が熱い傾向があるため、この違いによって温帯と熱帯の季節に関する概念が違う原因になるわけです。

ちなみに、ちょうど北回帰線にある場所であれば夏至は太陽が天頂に昇る日です。その一方、赤道にある場所では太陽が天頂に昇る日は春分と秋分の日となります。

終わりに

以上太陽の位置について色んなことを説明をしました。こうやって自然にある色んな現象が説明できて面白いです。天文学は難しいこといっぱいありますが、理解できたらどんどん楽しくなるのです。プログラミングはそれを簡単に理解できるようにする便利な魔法みたいなものです。コンピュータの発達した時代に生まれて、昔の人達よりずっと整った環境で勉強できるのはいいことです。

でもコンピュータを使わずに何年の時間をかけてずっと観測して天体の動きの原理に辿り着けるようになった昔の天文学者達その方がやはり凄くて立派です。